Fluid Dynamics Viscosity Poiseuilles Equation Coanda Effect From

Fluid Dynamics Viscosity, Poiseuille’s Equation, Coanda Effect

From ideal fluids to real fluids So far, we have considered ideal fluids: • They coast along with no difference in pressure • An ideal milk shake would be as easy to drink as a watery soda • The primary difference between ideal fluids and real fluids is their viscosity.

Viscosity Honey and water have almost identical densities, but their flow properties are dramatically different. Viscosity: measure of a fluid’s resistance to flow blood flow flight curve ball

Factors that affect flow of fluids • Pressure difference • How hard is fluid being pushed forward minus how hard fluid is being pushed back • Radius of tube • Harder to push fluids through narrower tubes • Length of tube • Longer tubes offers more resistance • Viscosity of fluid • Water flows more easily than molasses

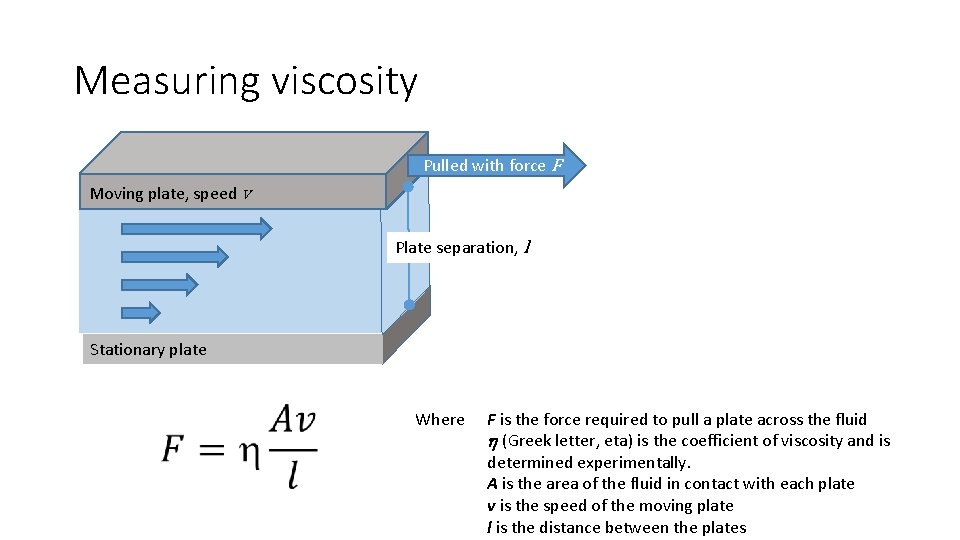
Measuring viscosity Pulled with force F Moving plate, speed v Plate separation, l Stationary plate Where F is the force required to pull a plate across the fluid (Greek letter, eta) is the coefficient of viscosity and is determined experimentally. A is the area of the fluid in contact with each plate v is the speed of the moving plate l is the distance between the plates

Coefficient of viscosity • Fluid (P s) Air (20 C) 1. 8 x 10 -5 Water (20 C) 1. 0 x 10 -3 Water (40 C) 0. 7*10 -3 Water (60 C) 0. 5*10 -3 Blood (37 C) 2. 5*10 -3 Motor oil (-30 C) 3. 0*105 Motor oil (40 C) 0. 07 Motor oil (100 C) 0. 01 Honey (15 C) 600 Honey (40 C) 20

For situations with laminar flow, Poiseuille’s equation •

Turbulent flow •

Solids traveling through viscous fluids • Lift • Coandă Effect http: //en. wikipedia. org/wiki/Coand%C 4%83_effect • Demo: cylindrical object in stream of water • Coanda planes, proof of concept physics

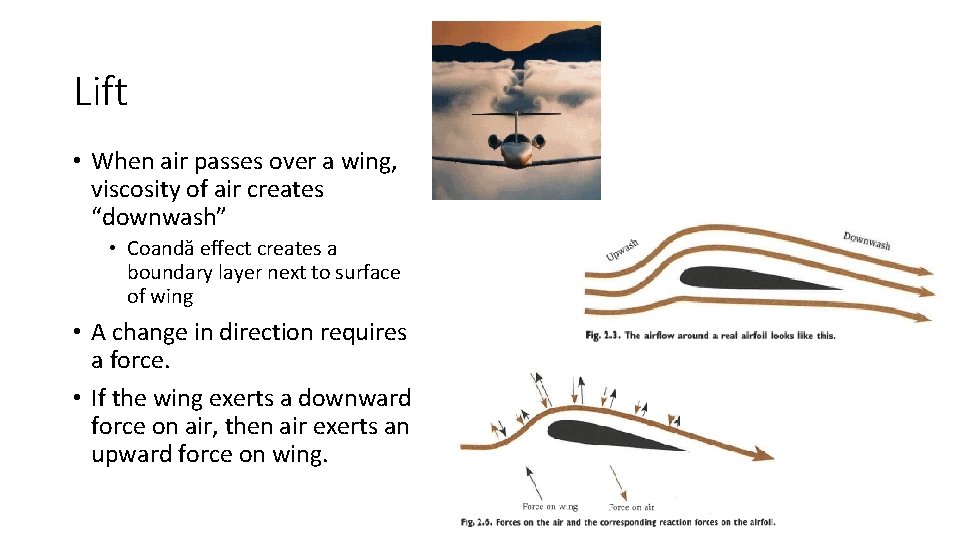
Lift • When air passes over a wing, viscosity of air creates “downwash” • Coandă effect creates a boundary layer next to surface of wing • A change in direction requires a force. • If the wing exerts a downward force on air, then air exerts an upward force on wing.

Drag •

Example Estimate the drag on a car traveling at 27 m/s (60 mph). Assume the drag coefficient for a well-designed car is 0. 5, air = 1. 3 kg/m 3, and the frontal area of the car is 3. 0 m 2. G U E S S CD=0. 5 A = 3. 0 m 2 For more experimentally determined values of coefficient of drag, check Engineering Toolbox and Wikipedia (yea, science nerds!)

Example Estimate the terminal velocity of a 60 -kg skydiver who has a surface area of 1. 5 m 2 and an assumed CD of 0. 6. G U E S S CD=0. 6 A = 1. 5 m 2