Fluid Animation CSE 35415541 By Matt Boggus Overview

Fluid Animation CSE 3541/5541 By: Matt Boggus

Overview • Procedural approximations • Mathematical background • Computational models for representing fluids • Using the computational models – Forces – “Stable fluids” by Stam

Real-time fluids • Goals: – Cheap to compute – Low memory consumption – Stability – Plausibility – Interactivity • Simulate the effect, not the cause

Real-time fluids • Procedural water – Unbounded surfaces, oceans • Particle systems – Splashing, spray, puddles, smoke, bubbles, rain • Heightfield fluids – Ponds, lakes, rivers

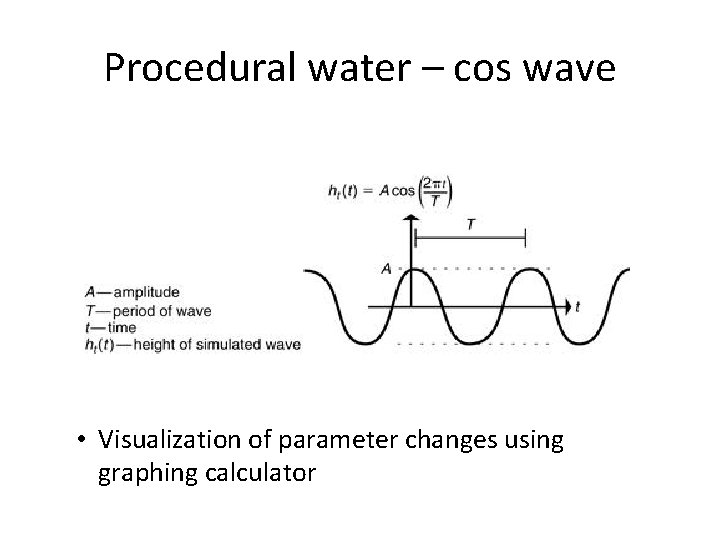
Procedural water – cos wave • Visualization of parameter changes using graphing calculator

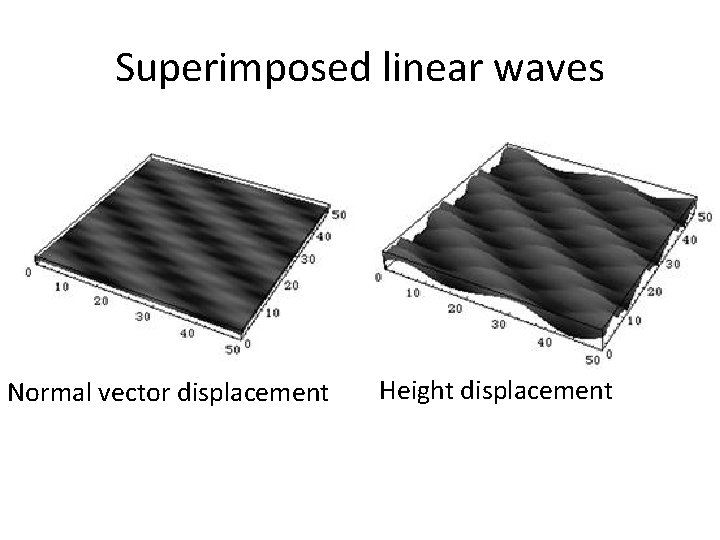
Superimposed linear waves Normal vector displacement Height displacement

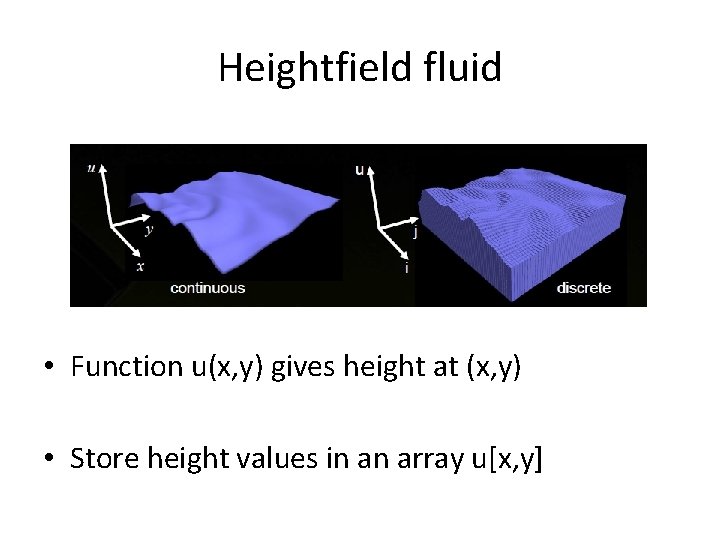
Heightfield fluid • Function u(x, y) gives height at (x, y) • Store height values in an array u[x, y]

Can this wave be represented using a heightfield?

Setting and updating heightfield fluids • Methods – Pressure or height differences between cells – Collision detection and displacement • Additional considerations – When updating, a second heightfield may be used to preserve the values from the previous frame – Handle boundary cases differently

Pressure/Height differences Initialize u[i, j] with some interesting function Initialze v[i, j]=0 loop v[i, j] += (u[i-1, j] + u[i+1, j] + u[i, j-1] + u[i, j+1])/4 – u[i, j] v[i, j] *= 0. 99 u[i, j] += v[i, j] endloop Clamp at boundary

Example videos • Real-Time Eulerian Water Simulation – Grid based – https: //www. youtube. com/watch? v=Jl 54 WZtm 0 Q E • SPH based real-time liquid simulation – Particle based – https: //www. youtube. com/watch? v=6 CP 5 Qvfu. D_ w

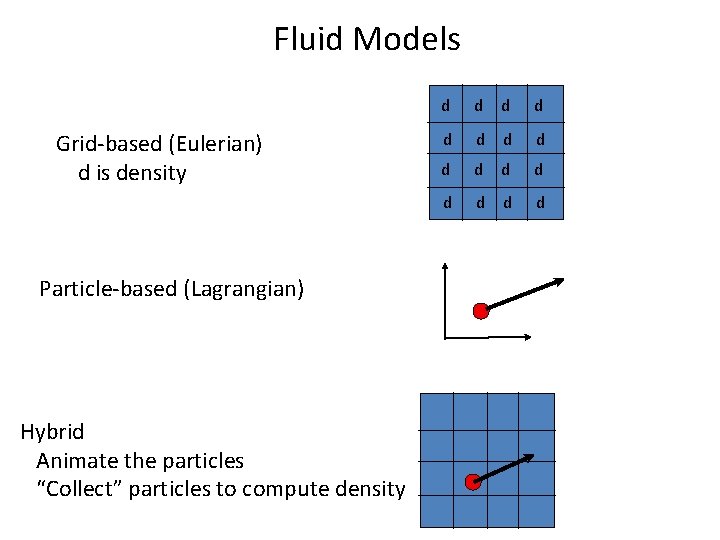
Fluid Models Grid-based (Eulerian) d is density Particle-based (Lagrangian) Hybrid Animate the particles “Collect” particles to compute density d d d d

Navier-Stokes Equation • Momentum equation ut = k 2 u –(u )u – p + f Change in Diffusion/ velocity Viscosity • Incompressibility u=0 Advection Pressure Body Forces u: the velocity field k: kinematic viscosity

Diffusion/Viscosity Force • Limit shear movement of particles in the liquid • The momentum between the neighbour particles are exchanged Pp Ppn

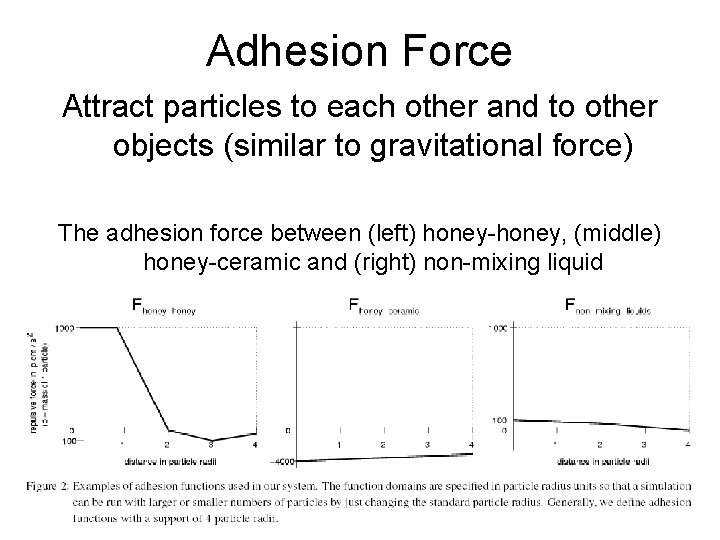
Adhesion Force Attract particles to each other and to other objects (similar to gravitational force) The adhesion force between (left) honey-honey, (middle) honey-ceramic and (right) non-mixing liquid

Advection Force Velocity grid

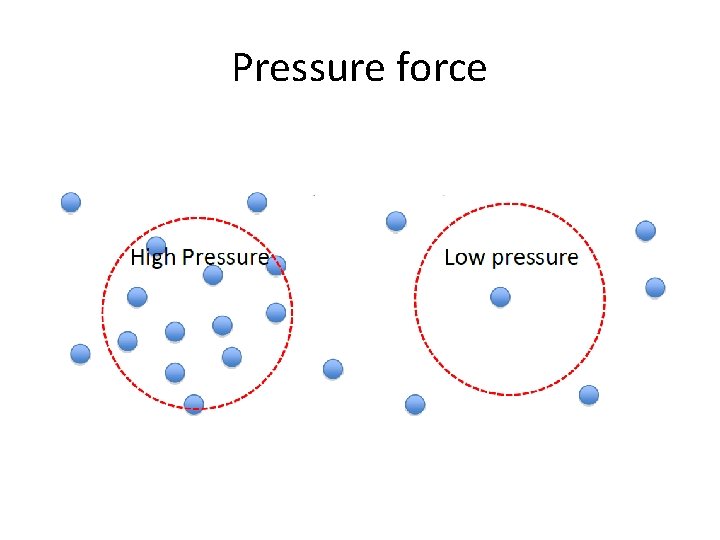
Pressure force

Pressure force

Friction Force • Dampen movement of particles in contact with objects in the environment • Scale down the velocity by a constant value

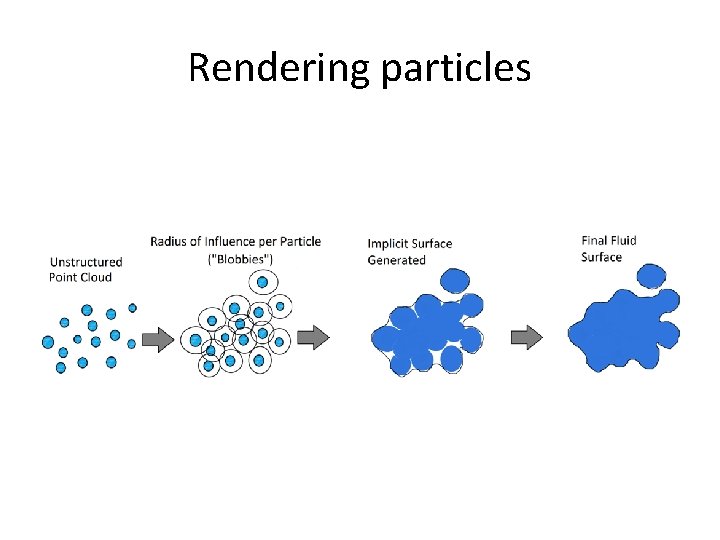
Rendering particles

Heightfield mesh particle collection Step 1. Zero out all u[i, j] Step 2. For each u[i, j], determine which particles are closet to it (bounding box collision test) Alternative Step 2. For each particle, determine which (i, j) it is closest to (translate position half a cell, then floor it)

Case Study: A 2 D Fluid Simulator • • Incompressible, viscous fluid Assuming the gravity is the only external force No inflow or outflow Constant viscosity, constant density everywhere in the fluid

Stable Fluids – overview of data Velocity grid Density grid Move densities around using velocity grid and dissipate densities Move velocities around using velocity grid and dissipate velocities Walkthrough: http: //www. dgp. utoronto. ca/~stam/reality/Talks/Fluids. Talk. Notes. pdf Source code: http: //www. autodeskresearch. com/publications/games

Additional readings • Fluid Simulation for Computer Animation (SIGGRAPH course) • The original stable fluids paper • An update to the stable fluids work • Fast Water Simulation for Games Using Height Fields (GDC talk)

ADDITIONAL SLIDES

Heightfield mesh creation and cell iteration • Covered earlier with terrains

Heightfield or Heightmap terrain data 2 D greyscale image Surface in 3 D space Images from http: //en. wikipedia. org/wiki/Heightmap

Heightfield mesh creation and cell iteration u[x, y] ; dimensions n by n

Heightfield mesh creation and cell iteration Quad[i, j] such that i = 0, j = 0; Vertices are U[0, 0], U[1, 1], U[0, 1] U[i, j], U[i+1, j+1], U[i, j+1]

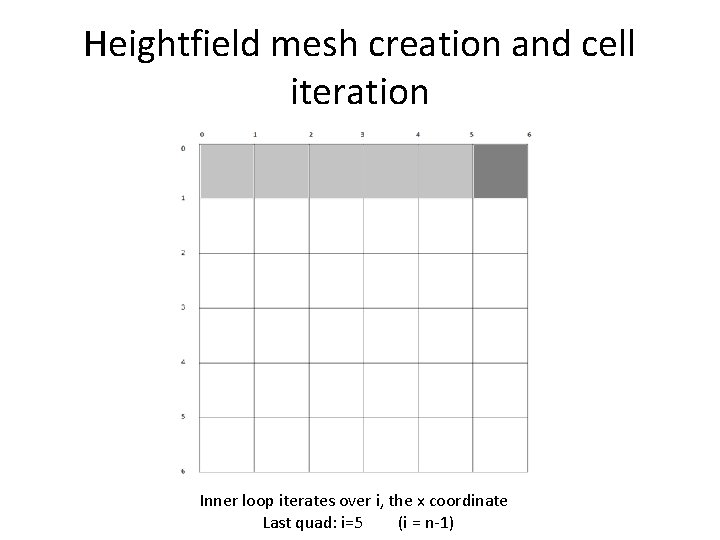
Heightfield mesh creation and cell iteration Inner loop iterates over i, the x coordinate Last quad: i=5 (i = n-1)

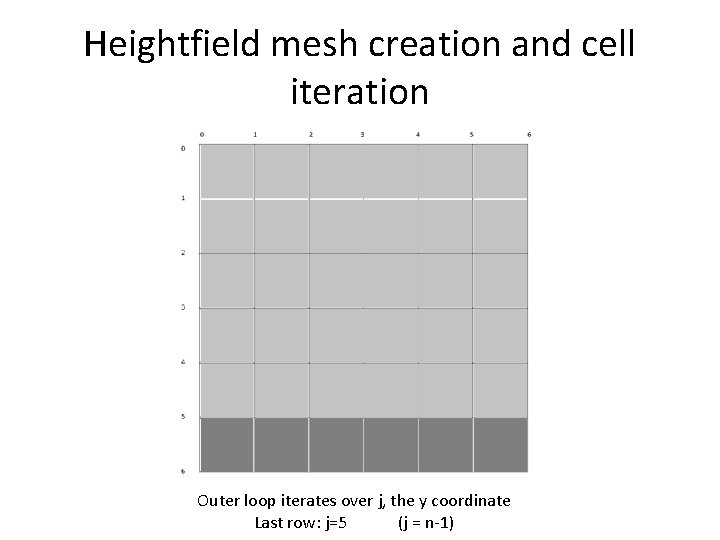
Heightfield mesh creation and cell iteration Outer loop iterates over j, the y coordinate Last row: j=5 (j = n-1)

Smoothing • For every grid cell u[i, j], set it to average of itself and neighbors • Implementation concerns: – A. looping order – B. boundary cases – C. both – D. none