Flow Over Immersed Bodies General External Flow Characteristics

Flow Over Immersed Bodies General External Flow Characteristics

General External Flow Characteristics • Many situations involve flow past objects • Such flow is termed external flow • Both theoretical and experimental approaches are used to study external flows • For external flows it is easier to use a coordinate system fixed to the object, i. e. to consider the fluid flowing past a stationary body with velocity U, the upstream velocity • Shape of the body affects the flow characteristics
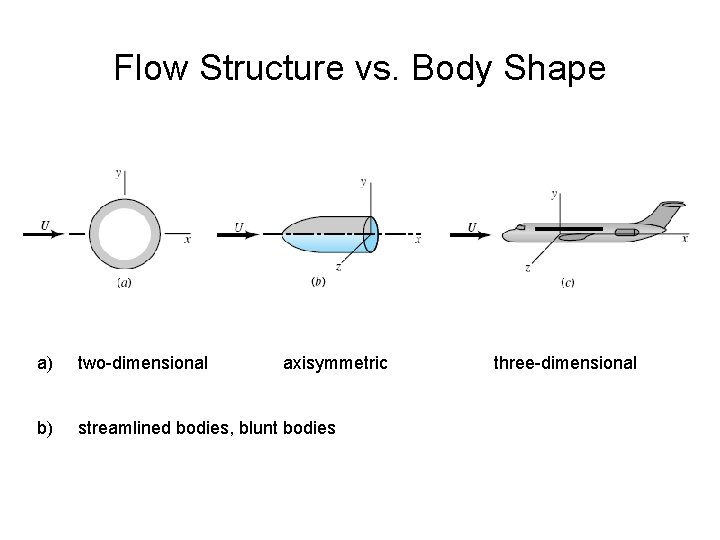
Flow Structure vs. Body Shape a) two-dimensional axisymmetric b) streamlined bodies, blunt bodies three-dimensional
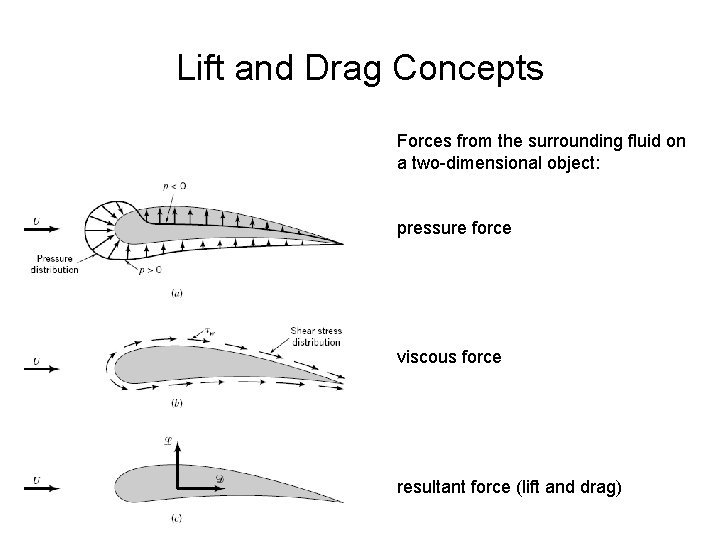
Lift and Drag Concepts Forces from the surrounding fluid on a two-dimensional object: pressure force viscous force resultant force (lift and drag)
Lift and Drag Concepts
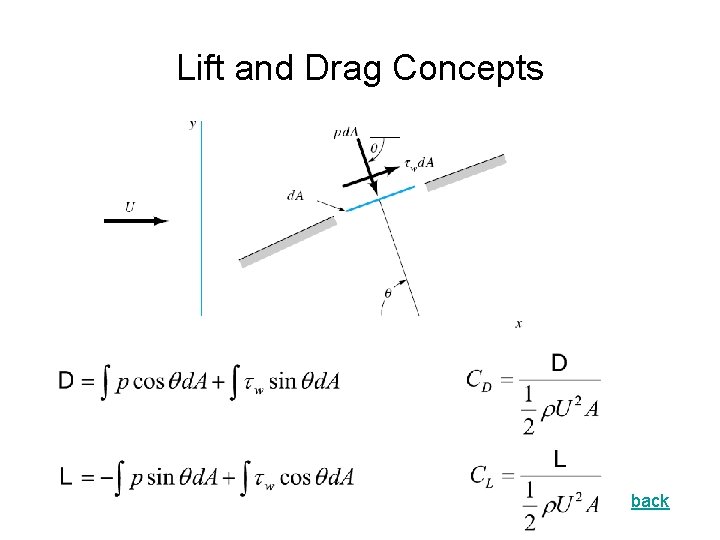
Lift and Drag Concepts back
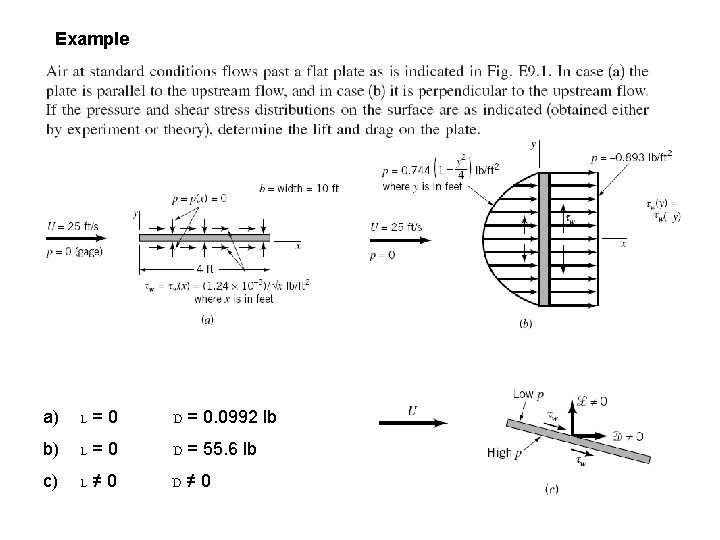
Example a) L=0 D = 0. 0992 lb b) L=0 D = 55. 6 lb c) L≠ 0 D≠ 0

Characteristics of Flow Past an Object • Character of the flow is function of the shape of the body • For a given-shaped body, characteristics of the flow depends on the value of Reynolds number • For most external flows – 10 < Re < 109 • As a rule of thumb, flows with Re > 100 are dominated by inertia effects, whereas flows with Re < 1 are dominated by viscous effects

Characteristics of Flow Past an Object Characteristics of the steady, viscous flow past a flat plate parallel to the upstream velocity: a) low Reynolds number flow, b) moderate Reynolds number flow, c) large Reynolds number flow
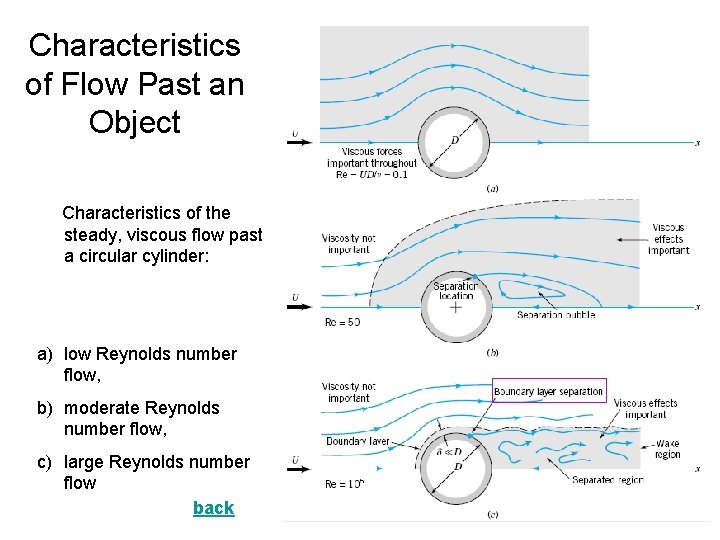
Characteristics of Flow Past an Object Characteristics of the steady, viscous flow past a circular cylinder: a) low Reynolds number flow, b) moderate Reynolds number flow, c) large Reynolds number flow back
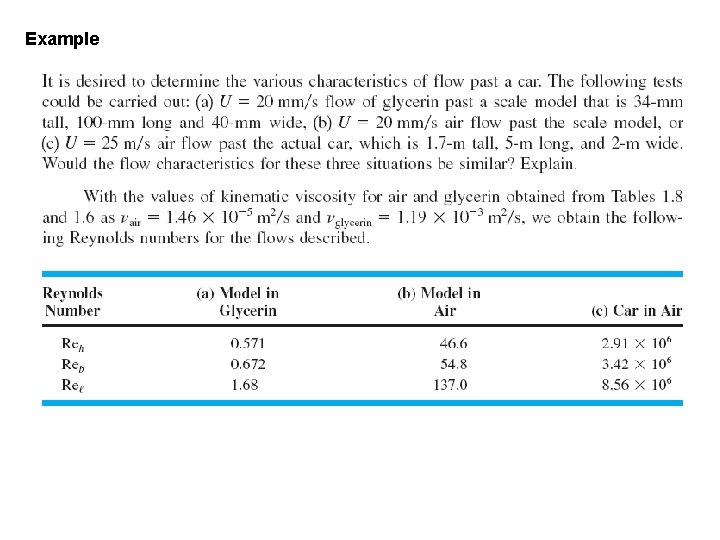
Example

Boundary Layer Characteristics
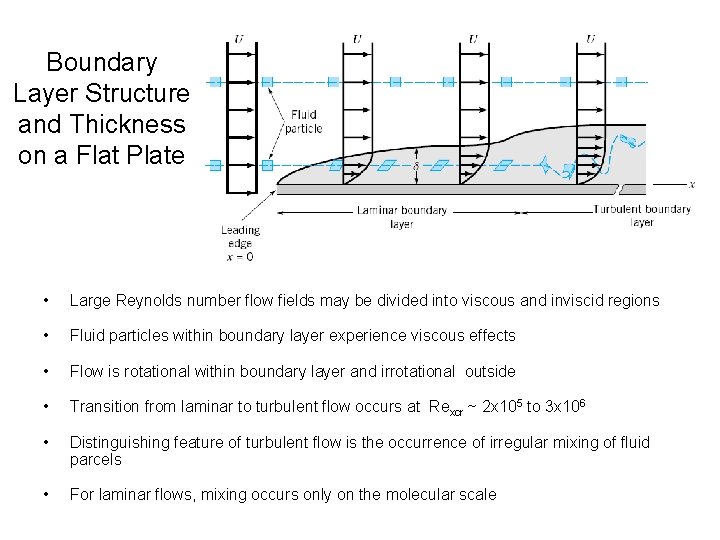
Boundary Layer Structure and Thickness on a Flat Plate • Large Reynolds number flow fields may be divided into viscous and inviscid regions • Fluid particles within boundary layer experience viscous effects • Flow is rotational within boundary layer and irrotational outside • Transition from laminar to turbulent flow occurs at Rexcr ~ 2 x 105 to 3 x 106 • Distinguishing feature of turbulent flow is the occurrence of irregular mixing of fluid parcels • For laminar flows, mixing occurs only on the molecular scale

Boundary Layer Thickness on a Flat Plate • Three boundary layer thickness definitions are used in boundary layer analysis: – standard boundary layer thickness – boundary layer displacement thickness * – boundary layer momentum thickness
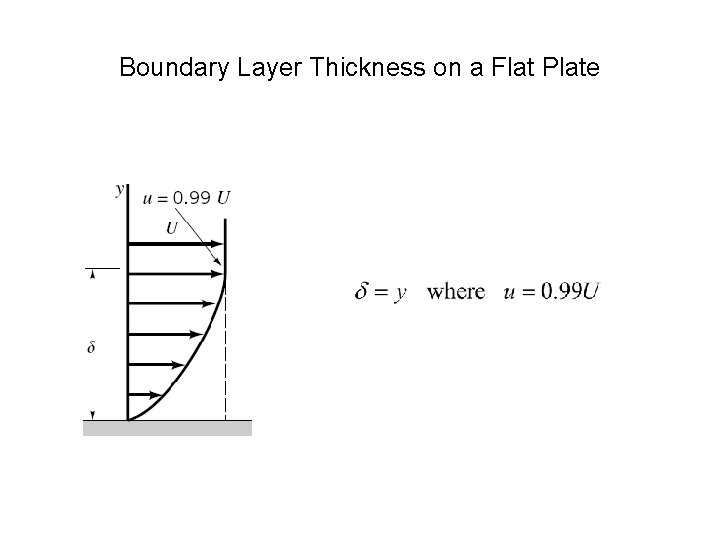
Boundary Layer Thickness on a Flat Plate
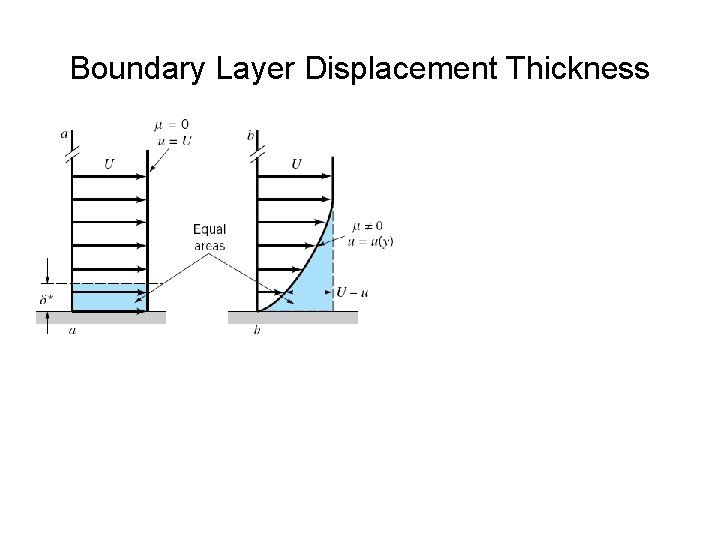
Boundary Layer Displacement Thickness
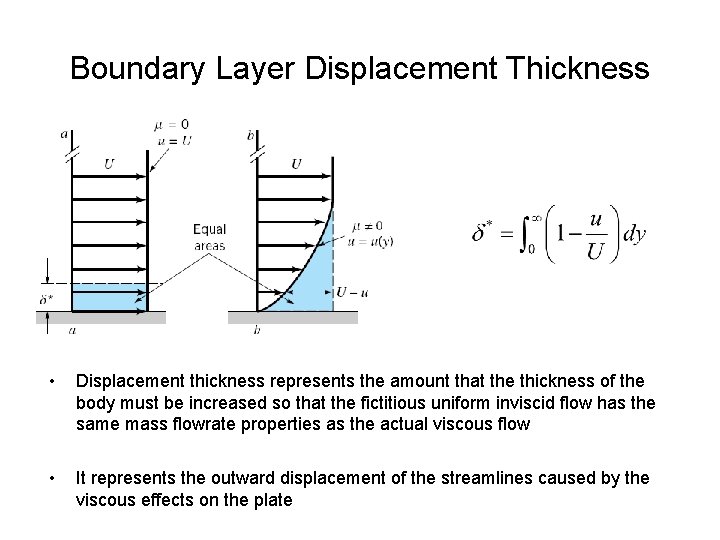
Boundary Layer Displacement Thickness • Displacement thickness represents the amount that the thickness of the body must be increased so that the fictitious uniform inviscid flow has the same mass flowrate properties as the actual viscous flow • It represents the outward displacement of the streamlines caused by the viscous effects on the plate
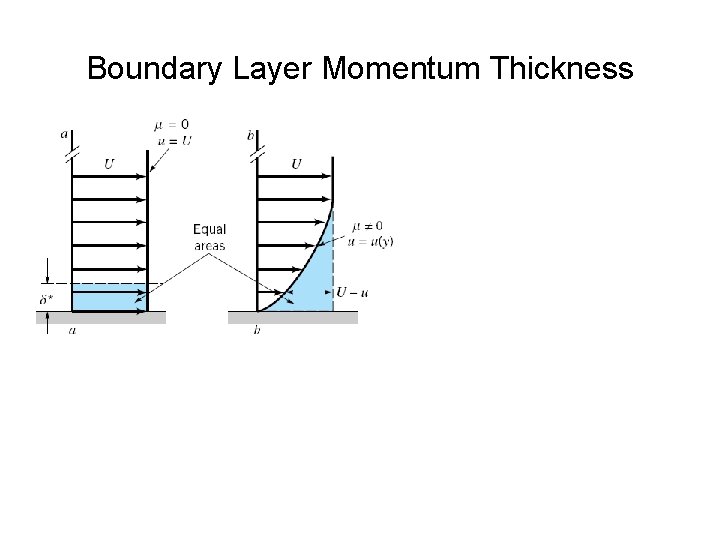
Boundary Layer Momentum Thickness
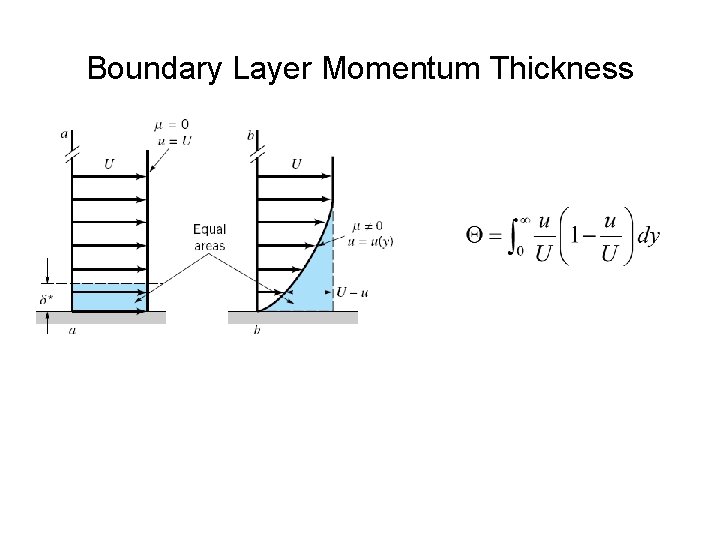
Boundary Layer Momentum Thickness
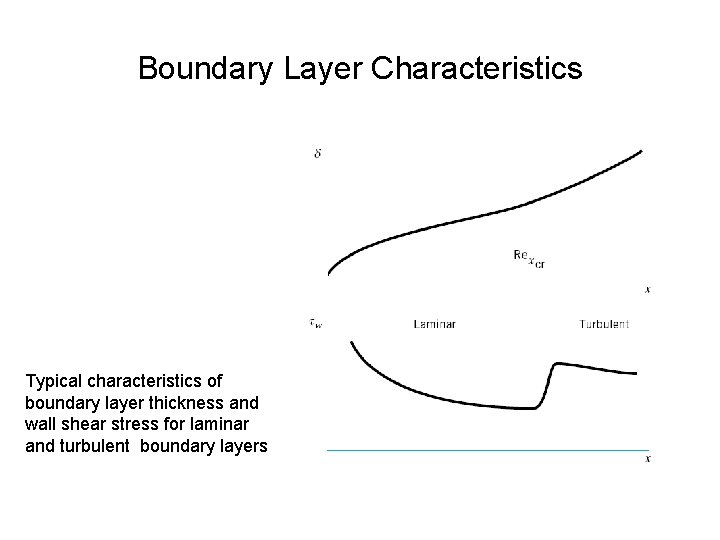
Boundary Layer Characteristics Typical characteristics of boundary layer thickness and wall shear stress for laminar and turbulent boundary layers

Prandtl/Blasius Boundary Layer Solution Equations governing steady, two-dimensional laminar flows with negligible gravitational effects are obtained from Navier-Stokes & continuity equations
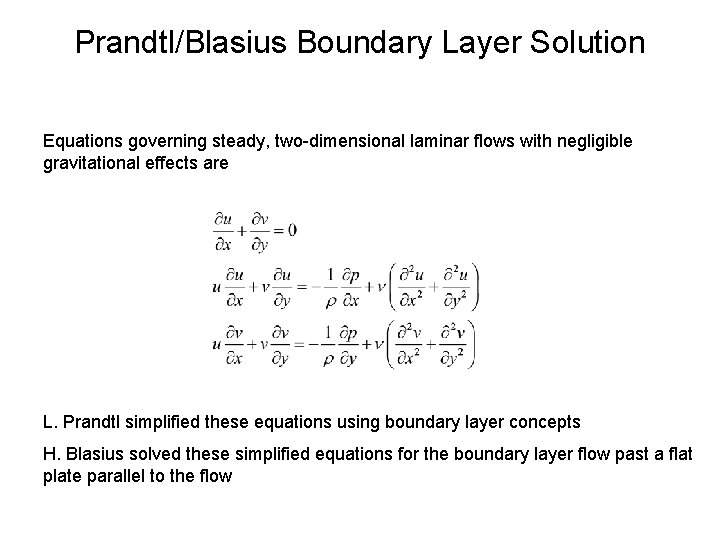
Prandtl/Blasius Boundary Layer Solution Equations governing steady, two-dimensional laminar flows with negligible gravitational effects are L. Prandtl simplified these equations using boundary layer concepts H. Blasius solved these simplified equations for the boundary layer flow past a flat plate parallel to the flow

Prandtl/Blasius Boundary Layer Solution Assumptions made: 1. 2. Pressure is constant throughout the fluid With these assumptions governing equations reduce to boundary layer equations:
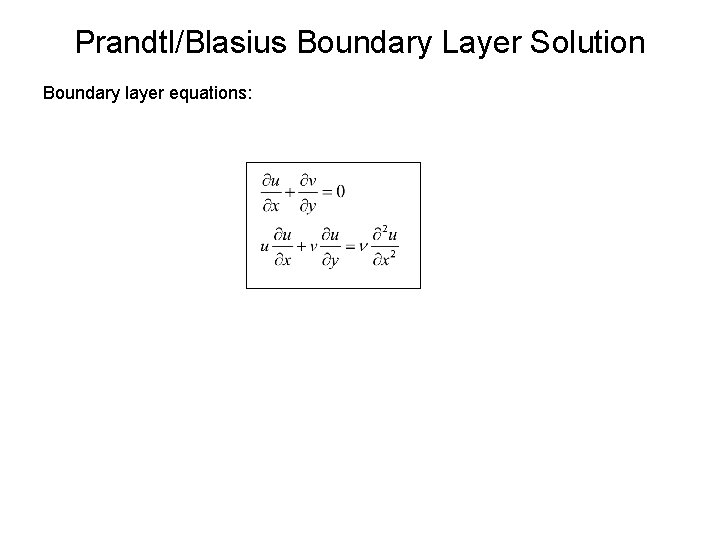
Prandtl/Blasius Boundary Layer Solution Boundary layer equations:
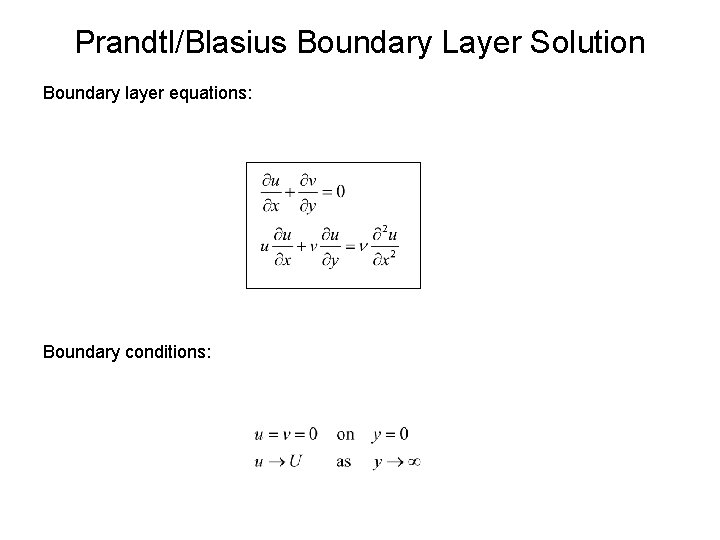
Prandtl/Blasius Boundary Layer Solution Boundary layer equations: Boundary conditions:

Prandtl/Blasius Boundary Layer Solution Further assumptions: 1. In dimensionless form boundary layer velocity profiles on a flat plate should be similar regardless on the location along the plate 2. Boundary layer thickness grows as the square root of x and inversely proportional to the square root of U

Prandtl/Blasius Boundary Layer Solution By introducing dimensionless similarity variable and the stream function velocity components become , where is unknown function, Substituting u and v into governing equations after manipulations gives Boundary conditions
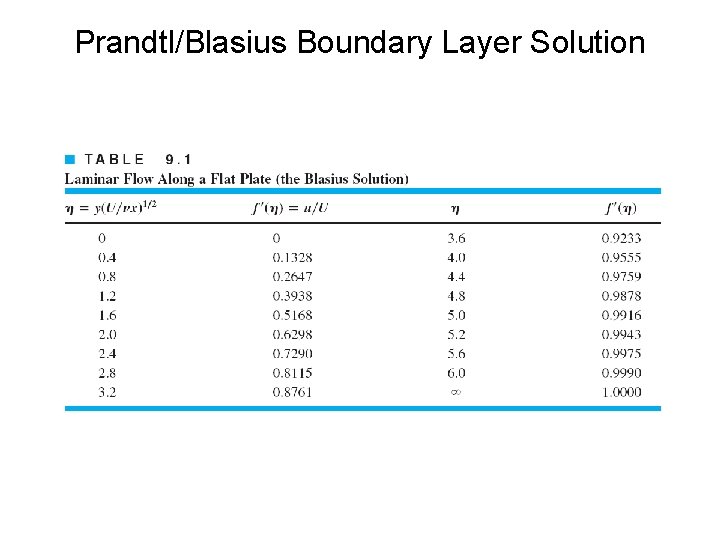
Prandtl/Blasius Boundary Layer Solution
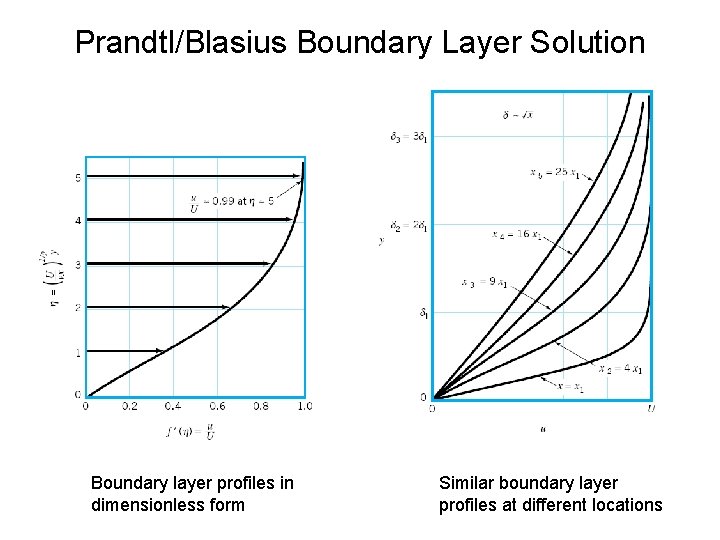
Prandtl/Blasius Boundary Layer Solution Boundary layer profiles in dimensionless form Similar boundary layer profiles at different locations
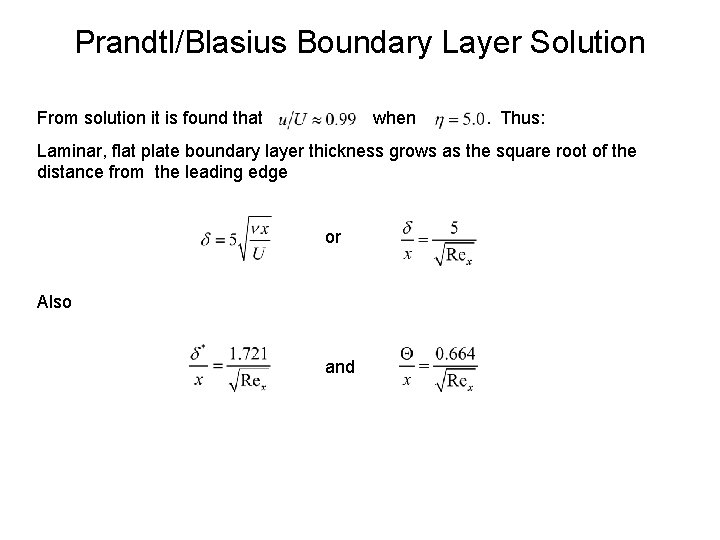
Prandtl/Blasius Boundary Layer Solution From solution it is found that when . Thus: Laminar, flat plate boundary layer thickness grows as the square root of the distance from the leading edge or Also and
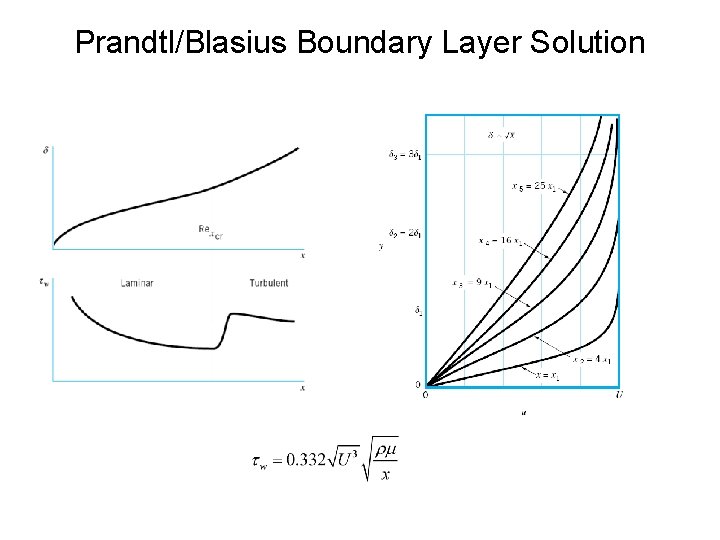
Prandtl/Blasius Boundary Layer Solution



Momentum Integral Boundary Layer Equation for a Flat Plate • Drag on a flat plate can be determined from Prandtl/Blasius boundary layer solution • An alternative is the Momentum Integral method • Momentum integral method provides an approximate technique to analyze boundary layer flow • To derive momentum integral boundary layer equation consider uniform flow past a flat plate and the fixed control volume
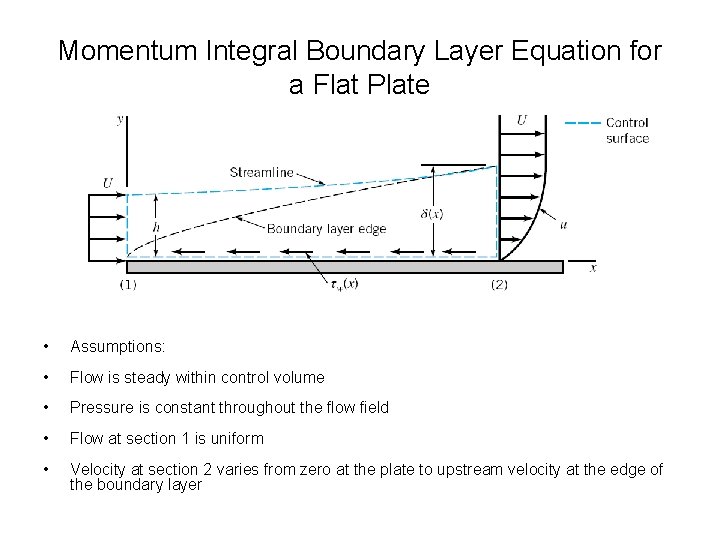
Momentum Integral Boundary Layer Equation for a Flat Plate • Assumptions: • Flow is steady within control volume • Pressure is constant throughout the flow field • Flow at section 1 is uniform • Velocity at section 2 varies from zero at the plate to upstream velocity at the edge of the boundary layer
Momentum Integral Boundary Layer Equation for a Flat Plate x component of the momentum equation
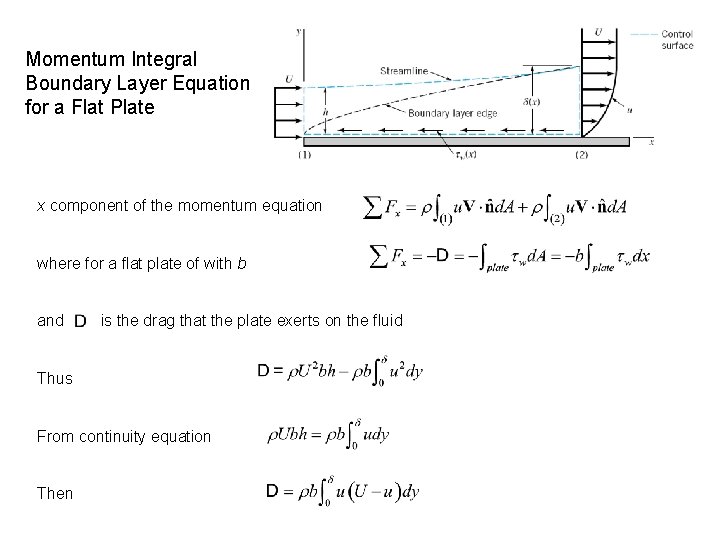
Momentum Integral Boundary Layer Equation for a Flat Plate x component of the momentum equation where for a flat plate of with b and is the drag that the plate exerts on the fluid Thus From continuity equation Then
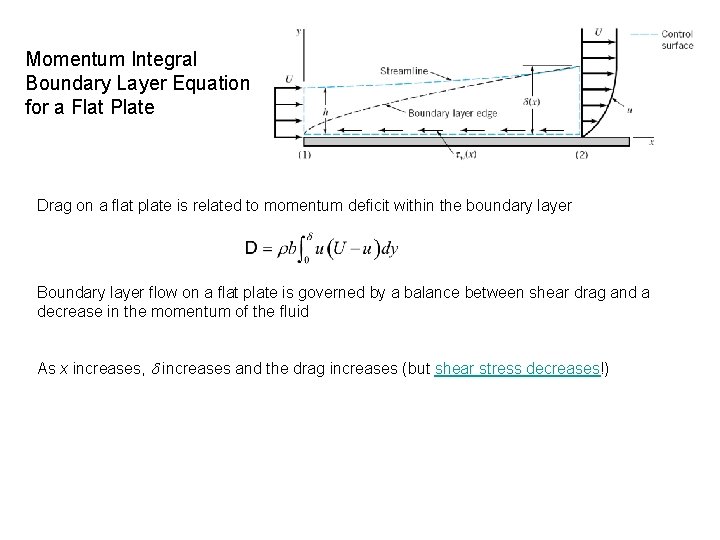
Momentum Integral Boundary Layer Equation for a Flat Plate Drag on a flat plate is related to momentum deficit within the boundary layer Boundary layer flow on a flat plate is governed by a balance between shear drag and a decrease in the momentum of the fluid As x increases, increases and the drag increases (but shear stress decreases!)
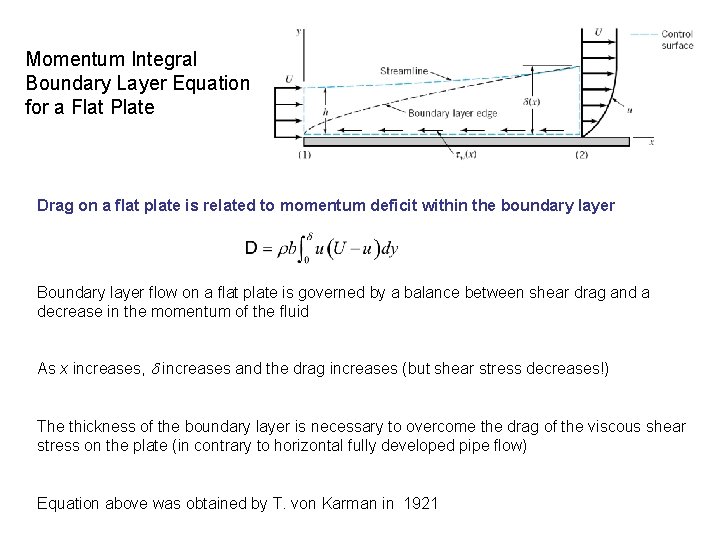
Momentum Integral Boundary Layer Equation for a Flat Plate Drag on a flat plate is related to momentum deficit within the boundary layer Boundary layer flow on a flat plate is governed by a balance between shear drag and a decrease in the momentum of the fluid As x increases, increases and the drag increases (but shear stress decreases!) The thickness of the boundary layer is necessary to overcome the drag of the viscous shear stress on the plate (in contrary to horizontal fully developed pipe flow) Equation above was obtained by T. von Karman in 1921
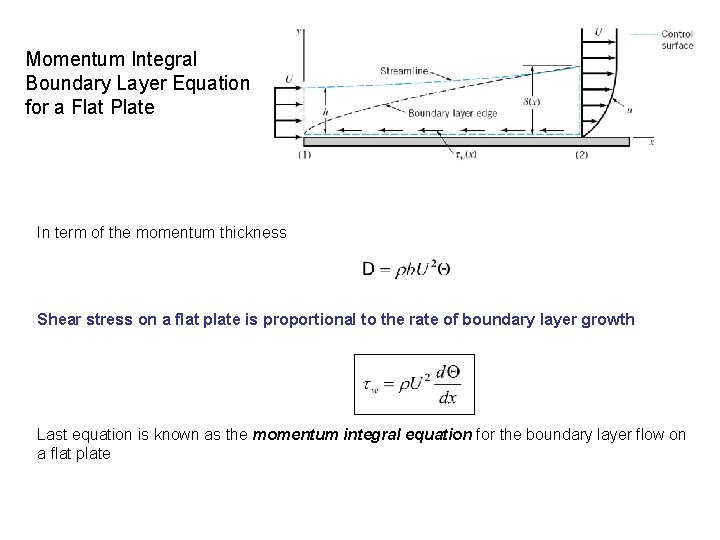
Momentum Integral Boundary Layer Equation for a Flat Plate In term of the momentum thickness Shear stress on a flat plate is proportional to the rate of boundary layer growth Last equation is known as the momentum integral equation for the boundary layer flow on a flat plate

Momentum-Integral Boundary Layer Method Usefulness of the momentum integral equation lies in ability to obtain approximate boundary layer results by using rather crude assumptions Even a rather crude guess at the velocity profile will allow us to obtain reasonable drag and shear stress results
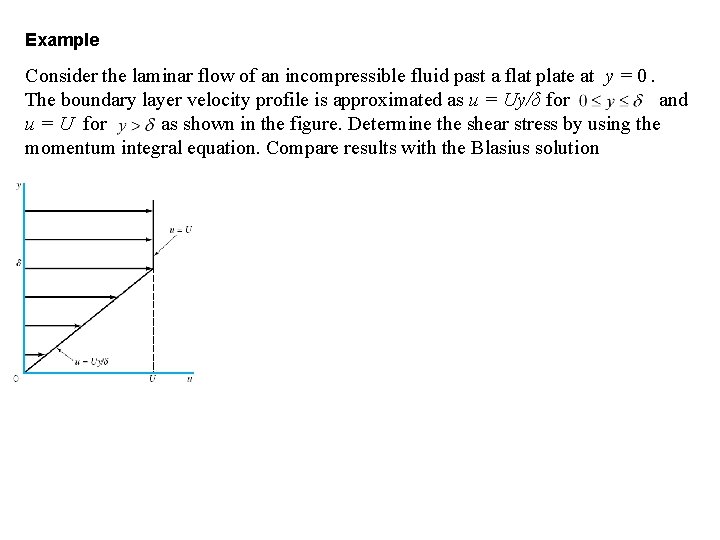
Example Consider the laminar flow of an incompressible fluid past a flat plate at y = 0. The boundary layer velocity profile is approximated as u = Uy/δ for and u = U for as shown in the figure. Determine the shear stress by using the momentum integral equation. Compare results with the Blasius solution

Example Consider the laminar flow of an incompressible fluid past a flat plate at y = 0. The boundary layer velocity profile is approximated as u = Uy/δ for and u = U for as shown in the figure. Determine the shear stress by using the momentum integral equation. Compare results with the Blasius solution

Momentum-Integral Boundary Layer Method • • In the previous example momentum integral equation was used along with the linear dimensionless velocity profile to obtain reasonable boundary layer results Accuracy of results depends on how closely the shape of the assumed profile approximates the actual profile

Momentum-Integral Boundary Layer Method Consider general velocity profile as a function of dimensionless coordinate Boundary conditions
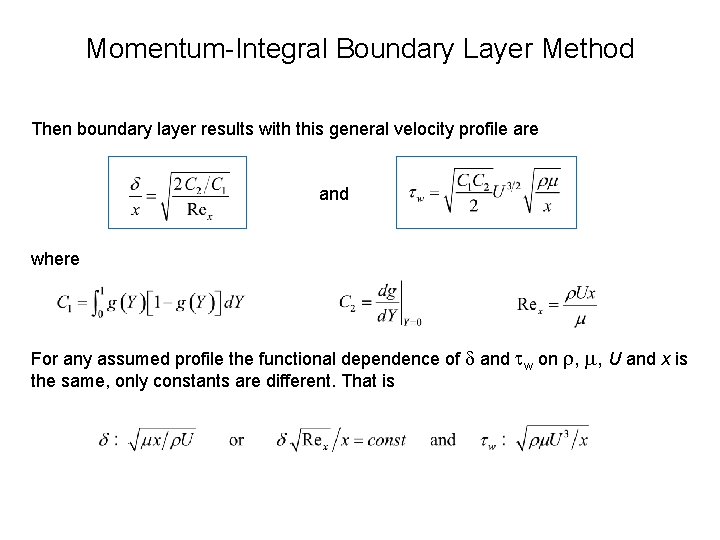
Momentum-Integral Boundary Layer Method Then boundary layer results with this general velocity profile are and where For any assumed profile the functional dependence of and w on , , U and x is the same, only constants are different. That is
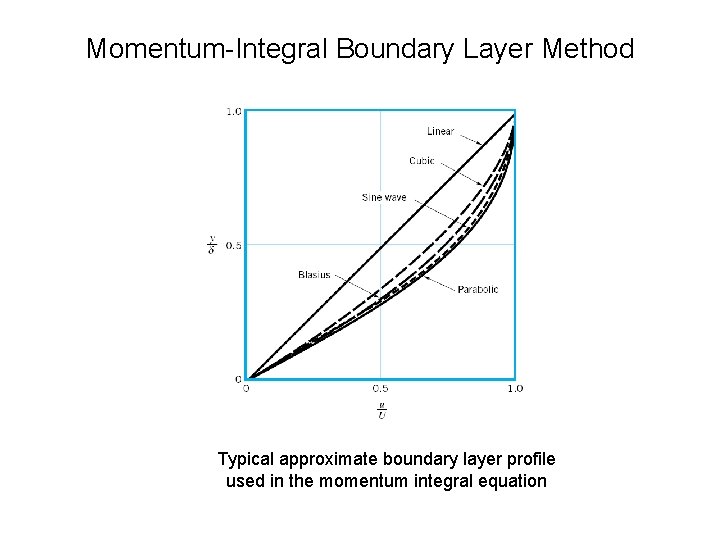
Momentum-Integral Boundary Layer Method Typical approximate boundary layer profile used in the momentum integral equation

Momentum-Integral Boundary Layer Method Local friction coefficient Friction drag

Momentum-Integral Boundary Layer Method Momentum Integral boundary method apply to boundary layer flows on curved surfaces and to turbulent flows

Transition from Laminar to Turbulent Flow The boundary layer on a flat plate will become turbulent if the plate is long enough On a flat plate with a sharp leading edge in a typical air stream, the transition from laminar to turbulent flow takes place at a distance x from the leading edge given by Unless otherwise stated, we will use in our calculations Turbulent spots and the transition from laminar to turbulent boundary layer flow on a flat plate. Flow from left to right
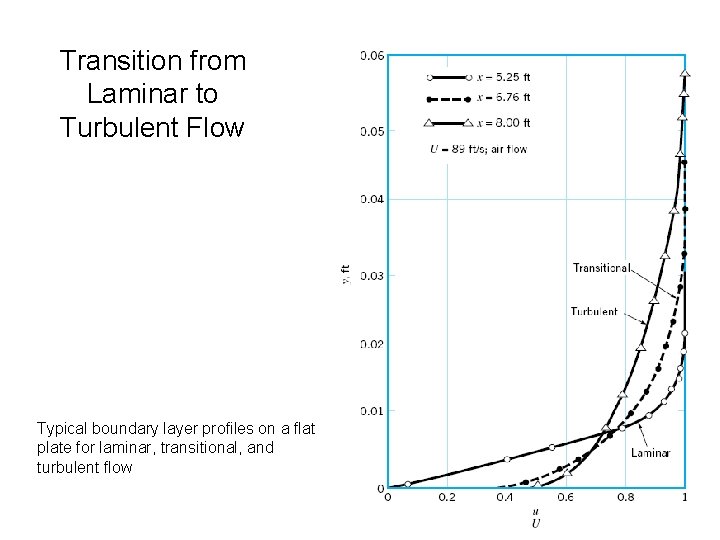
Transition from Laminar to Turbulent Flow Typical boundary layer profiles on a flat plate for laminar, transitional, and turbulent flow

Example A fluid flows steadily past a flat plate with a velocity of U = 10 ft/s. At approximately what location will the boundary layer become turbulent, and how thick is the boundary layer at that point if the fluid is (a) water at 60°F, (b) standard air, or (c) glycerin at 68 °F Solution Results

Turbulent Boundary Layer Flow • Structure of turbulent boundary layer is complex, random and irregular • Flow is the jumbled mix of eddies (swirls) of different size • Mass, momentum and energy are convected in x and y directions • Mass convection is small in y direction but there is considerable transfer of x component of momentum in y direction • Plate acts as a momentum sink, extracting momentum from fluid • Wall shear stress for turbulent boundary layer flow is greater than for laminar • There is no “exact” solution for turbulent boundary layer since there is no precise expression for shear stress in turbulent flow • Solution can be obtained by use of momentum integral equation. For that one need: – approximate velocity profile – empirical relation for wall shear stress • Also, progress is being made in numerical integration of Navier-Stokes equations
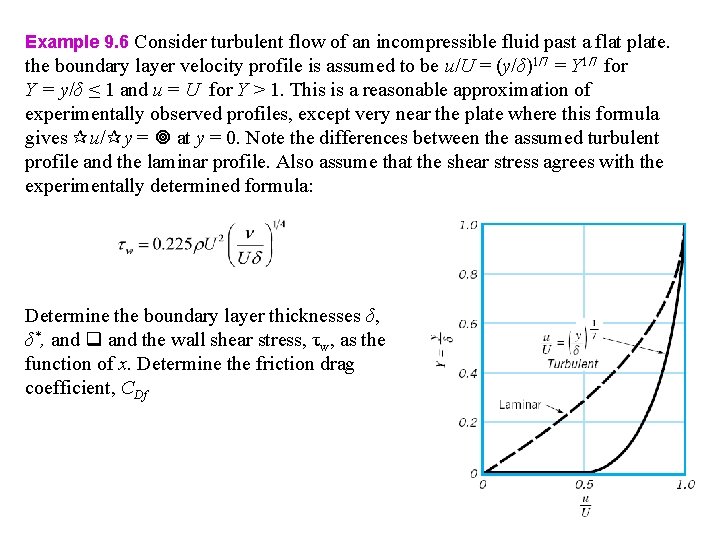
Example 9. 6 Consider turbulent flow of an incompressible fluid past a flat plate. the boundary layer velocity profile is assumed to be u/U = (y/δ)1/7 = Y 1/7 for Y = y/δ ≤ 1 and u = U for Y > 1. This is a reasonable approximation of experimentally observed profiles, except very near the plate where this formula gives u/ y = at y = 0. Note the differences between the assumed turbulent profile and the laminar profile. Also assume that the shear stress agrees with the experimentally determined formula: Determine the boundary layer thicknesses δ, δ*, and the wall shear stress, τw, as the function of x. Determine the friction drag coefficient, CDf



Comments Laminar boundary layer flow Turbulent boundary layer flow The random character of the turbulent flow causes a different structure of the flow
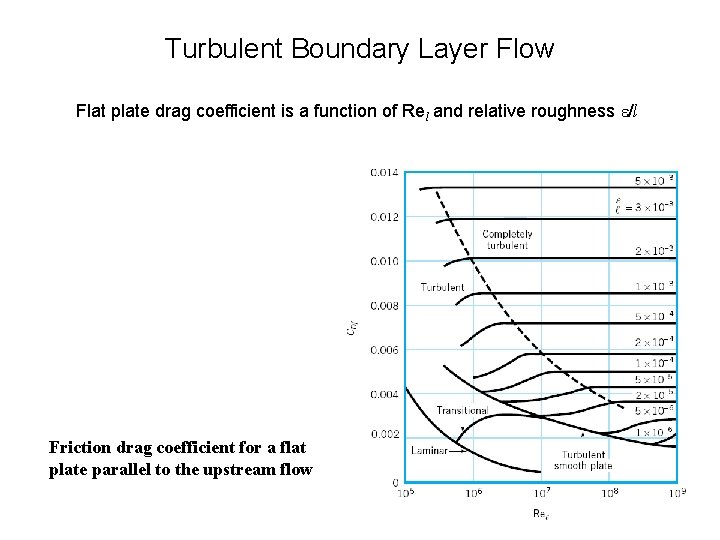
Turbulent Boundary Layer Flow Flat plate drag coefficient is a function of Rel and relative roughness /l Friction drag coefficient for a flat plate parallel to the upstream flow
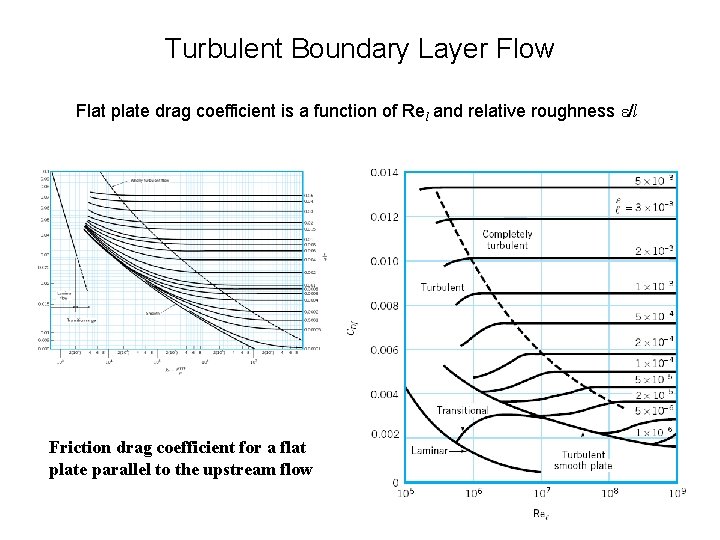
Turbulent Boundary Layer Flow Flat plate drag coefficient is a function of Rel and relative roughness /l Friction drag coefficient for a flat plate parallel to the upstream flow
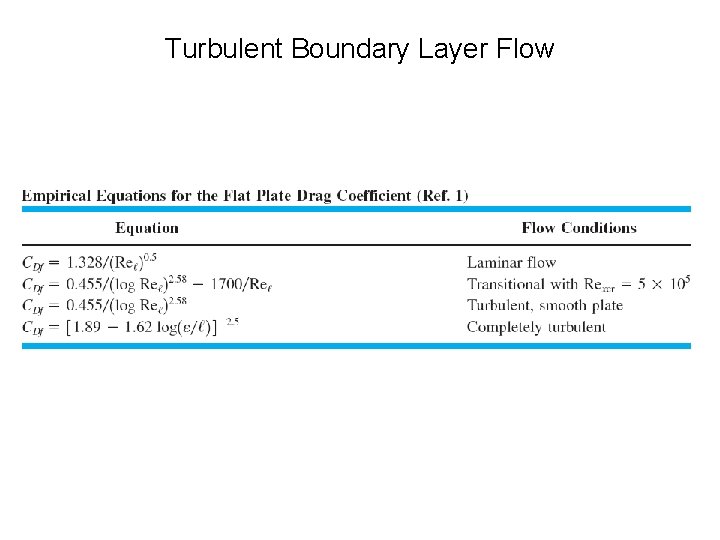
Turbulent Boundary Layer Flow

Effect of Pressure Gradient • For flow along a flat plate pressure is constant throughout • For flow past body other than flat plate the pressure is not uniform • Pressure variation in direction normal to the surface is small but pressure does vary along the body surface if surface is curved • Terminology: U – upstream velocity; Ufs – free-stream velocity, the fluid velocity at the edge of the boundary layer • Variation in Ufs causes pressure gradient in the boundary layer • Characteristics of the entire flow are dependent on the pressure gradient within the boundary layer • For a flat plate U = Ufs, for a curved surface body it is not
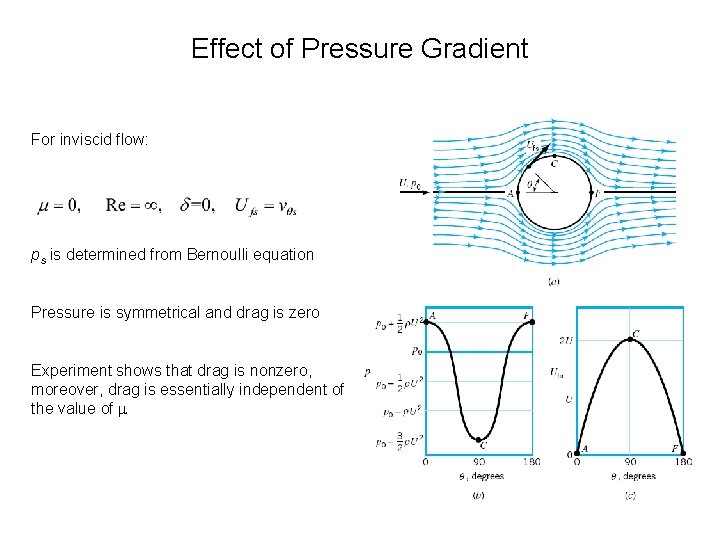
Effect of Pressure Gradient For inviscid flow: ps is determined from Bernoulli equation Pressure is symmetrical and drag is zero Experiment shows that drag is nonzero, moreover, drag is essentially independent of the value of
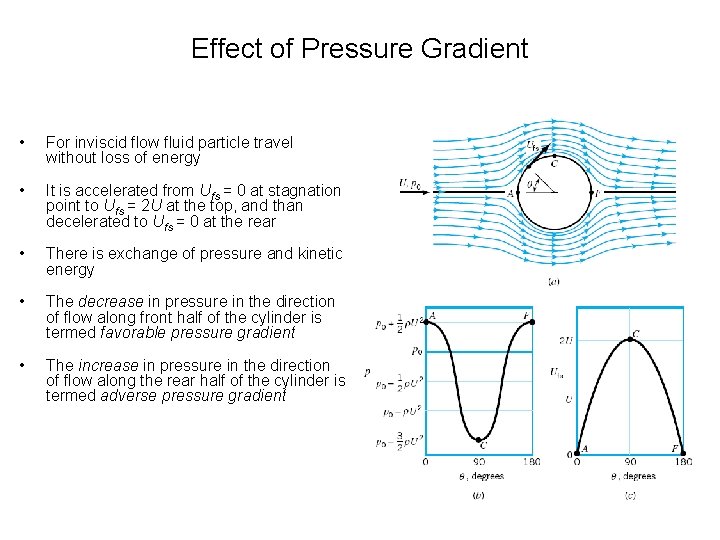
Effect of Pressure Gradient • For inviscid flow fluid particle travel without loss of energy • It is accelerated from Ufs = 0 at stagnation point to Ufs = 2 U at the top, and than decelerated to Ufs = 0 at the rear • There is exchange of pressure and kinetic energy • The decrease in pressure in the direction of flow along front half of the cylinder is termed favorable pressure gradient • The increase in pressure in the direction of flow along the rear half of the cylinder is termed adverse pressure gradient
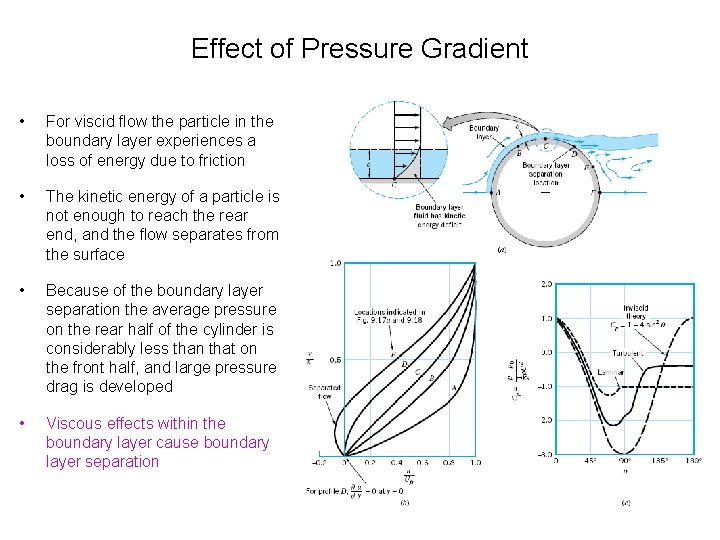
Effect of Pressure Gradient • For viscid flow the particle in the boundary layer experiences a loss of energy due to friction • The kinetic energy of a particle is not enough to reach the rear end, and the flow separates from the surface • Because of the boundary layer separation the average pressure on the rear half of the cylinder is considerably less than that on the front half, and large pressure drag is developed • Viscous effects within the boundary layer cause boundary layer separation
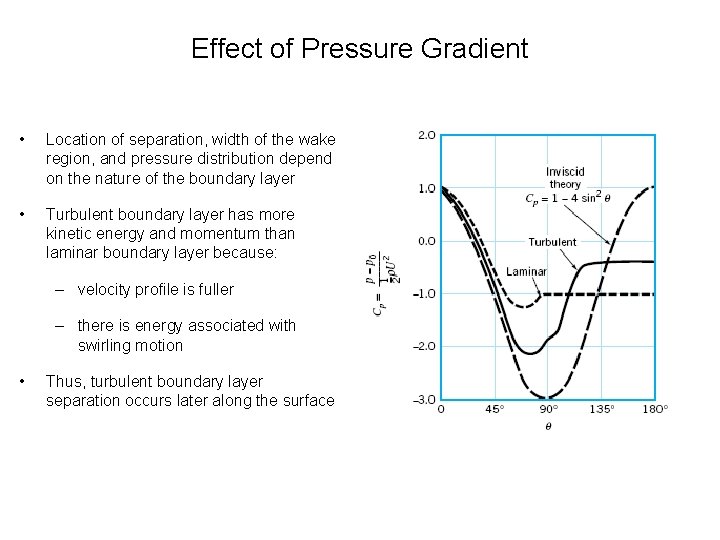
Effect of Pressure Gradient • Location of separation, width of the wake region, and pressure distribution depend on the nature of the boundary layer • Turbulent boundary layer has more kinetic energy and momentum than laminar boundary layer because: – velocity profile is fuller – there is energy associated with swirling motion • Thus, turbulent boundary layer separation occurs later along the surface

Drag and Lift

Generalized Formulae for Drag and Lift • Any object moving through fluid experience drag D • D is a net force in the direction of flow due to the pressure (pressure drag Dp) and shear forces (friction drag Df) on the surface of the object • If the object is not symmetrical, there may also be a force normal to the free stream – a lift L • Following generalized formulae can be used for drag and lift calculations: • Compare with eqs. 9. 1, 9. 2

Drag can be determined by use of equation if pressure distribution and wall shear stress are known. But they are difficult to determined analytically Most of information of drag is obtained from experiment Experimental results are given in the form of a drag coefficient: CD is a function of shape of the body, Reynolds number, Mach number, Froude number and relative roughness:

Friction Drag • Friction drag is a function of wall shear stress and orientation of a surface • Consider flat plate parallel and perpendicular to the flow • For blunt bodies and high Reynolds number flows contribution of the shear force to overall drag is quite small • For highly streamlined bodies and low Reynolds number flows most of the drag may be due to friction drag

Friction Drag Friction drag on a flat plate parallel to the flow can be calculated from or from Where friction drag coefficient can be obtained from Figure or Table

Friction Drag Friction drag on a flat plate parallel to the flow can be calculated from or from Where friction drag coefficient can be obtained from Figure or Table Wall shear stress along the surface of a curved body is difficult to determine. Approximate results may be obtained. If shear stress is known, friction drag can be determined
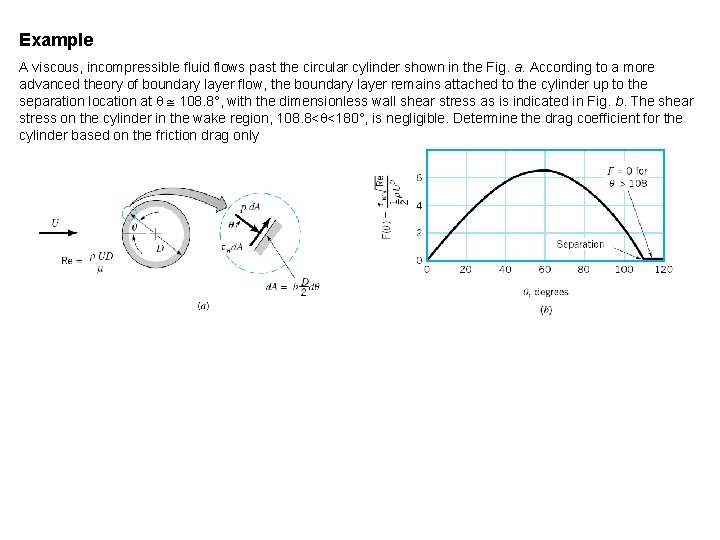
Example A viscous, incompressible fluid flows past the circular cylinder shown in the Fig. a. According to a more advanced theory of boundary layer flow, the boundary layer remains attached to the cylinder up to the separation location at 108. 8°, with the dimensionless wall shear stress as is indicated in Fig. b. The shear stress on the cylinder in the wake region, 108. 8< <180°, is negligible. Determine the drag coefficient for the cylinder based on the friction drag only
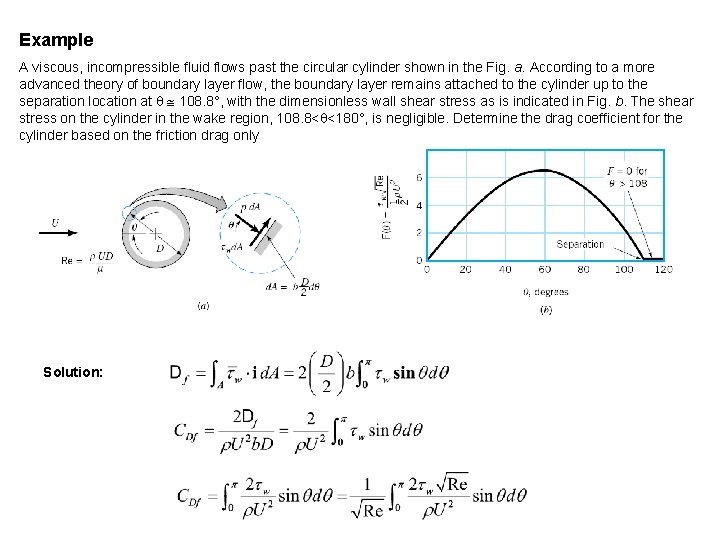
Example A viscous, incompressible fluid flows past the circular cylinder shown in the Fig. a. According to a more advanced theory of boundary layer flow, the boundary layer remains attached to the cylinder up to the separation location at 108. 8°, with the dimensionless wall shear stress as is indicated in Fig. b. The shear stress on the cylinder in the wake region, 108. 8< <180°, is negligible. Determine the drag coefficient for the cylinder based on the friction drag only Solution:
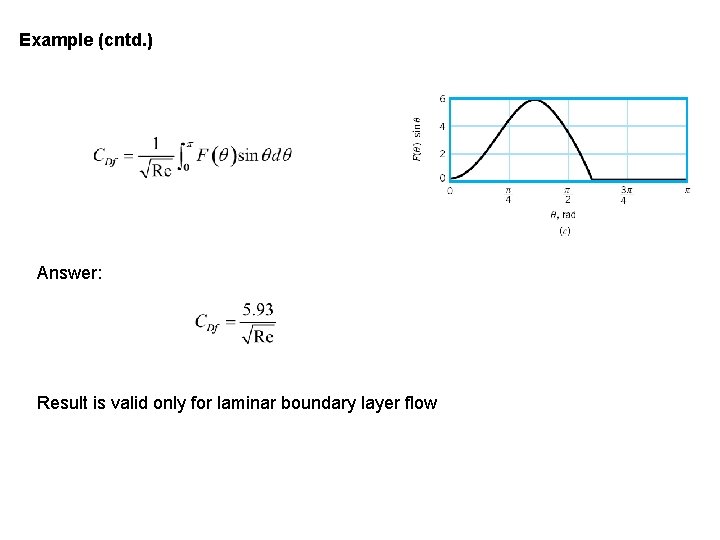
Example (cntd. ) Answer: Result is valid only for laminar boundary layer flow

Pressure Drag Pressure drag is produced by the normal stresses. Pressure (form) drag strongly depends of the body shape. It can be determined from or in terms of the pressure drag coefficient where pressure coefficient (dimensionless form of the pressure) For high Reynolds number flows CDp is relatively independent of Reynolds number For very small Reynolds number flows CDp is proportional to 1/Re
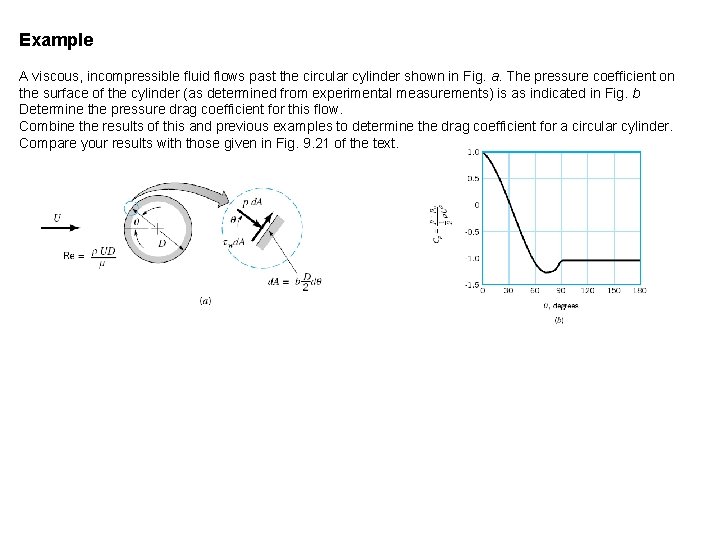
Example A viscous, incompressible fluid flows past the circular cylinder shown in Fig. a. The pressure coefficient on the surface of the cylinder (as determined from experimental measurements) is as indicated in Fig. b Determine the pressure drag coefficient for this flow. Combine the results of this and previous examples to determine the drag coefficient for a circular cylinder. Compare your results with those given in Fig. 9. 21 of the text.
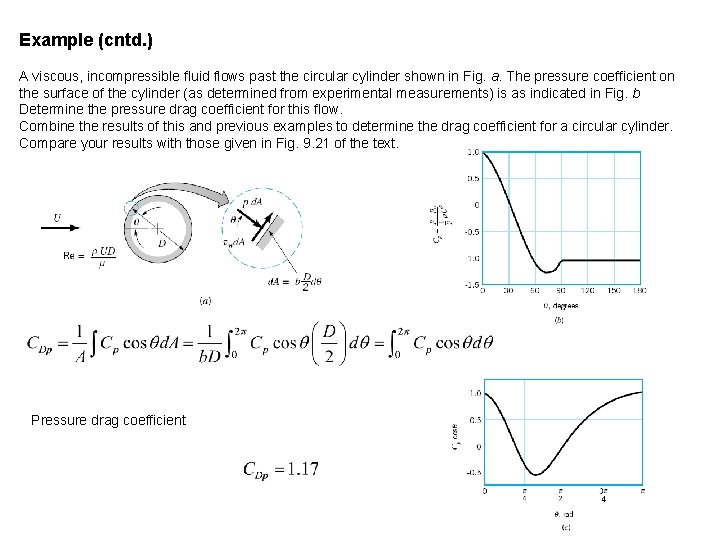
Example (cntd. ) A viscous, incompressible fluid flows past the circular cylinder shown in Fig. a. The pressure coefficient on the surface of the cylinder (as determined from experimental measurements) is as indicated in Fig. b Determine the pressure drag coefficient for this flow. Combine the results of this and previous examples to determine the drag coefficient for a circular cylinder. Compare your results with those given in Fig. 9. 21 of the text. Pressure drag coefficient
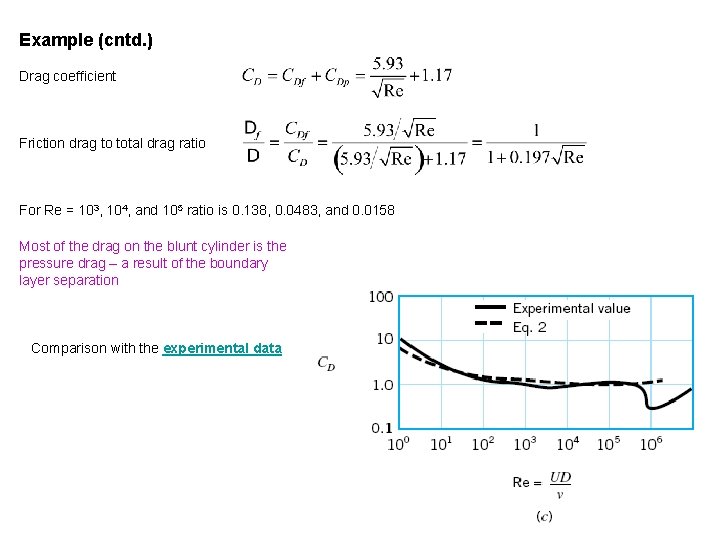
Example (cntd. ) Drag coefficient Friction drag to total drag ratio For Re = 103, 104, and 105 ratio is 0. 138, 0. 0483, and 0. 0158 Most of the drag on the blunt cylinder is the pressure drag – a result of the boundary layer separation Comparison with the experimental data
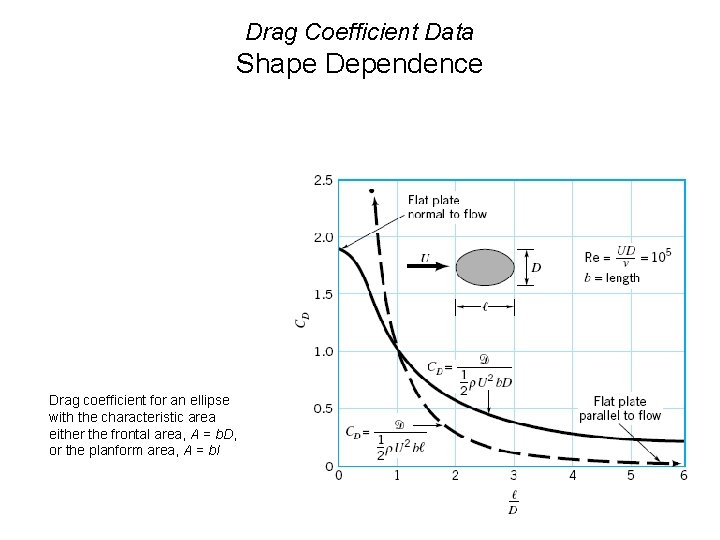
Drag Coefficient Data Shape Dependence Drag coefficient for an ellipse with the characteristic area either the frontal area, A = b. D, or the planform area, A = bl
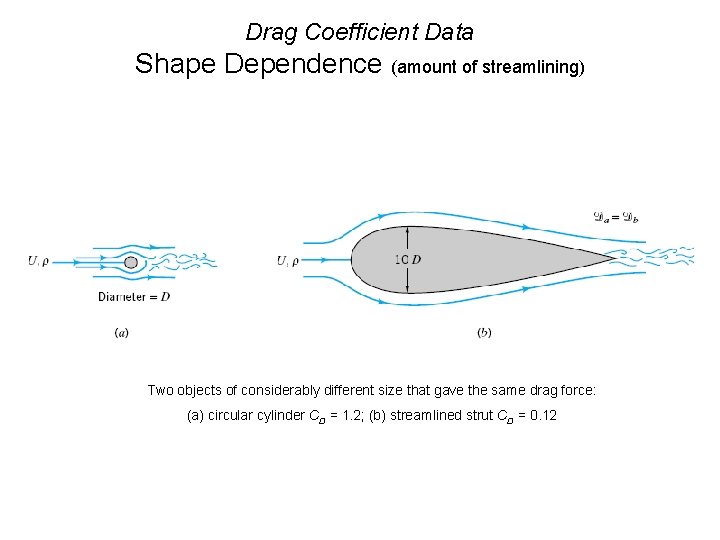
Drag Coefficient Data Shape Dependence (amount of streamlining) Two objects of considerably different size that gave the same drag force: (a) circular cylinder CD = 1. 2; (b) streamlined strut CD = 0. 12
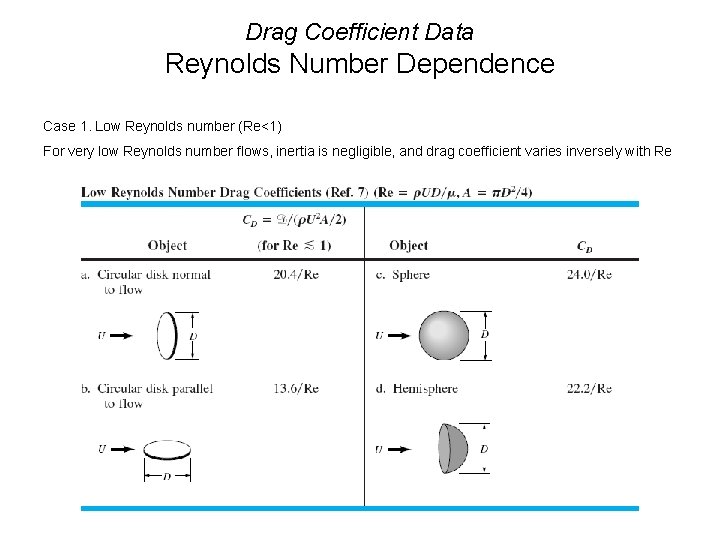
Drag Coefficient Data Reynolds Number Dependence Case 1. Low Reynolds number (Re<1) For very low Reynolds number flows, inertia is negligible, and drag coefficient varies inversely with Re
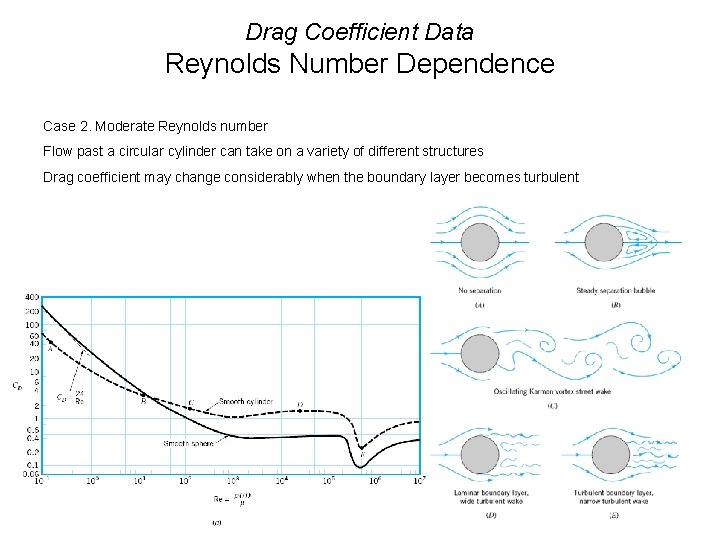
Drag Coefficient Data Reynolds Number Dependence Case 2. Moderate Reynolds number Flow past a circular cylinder can take on a variety of different structures Drag coefficient may change considerably when the boundary layer becomes turbulent
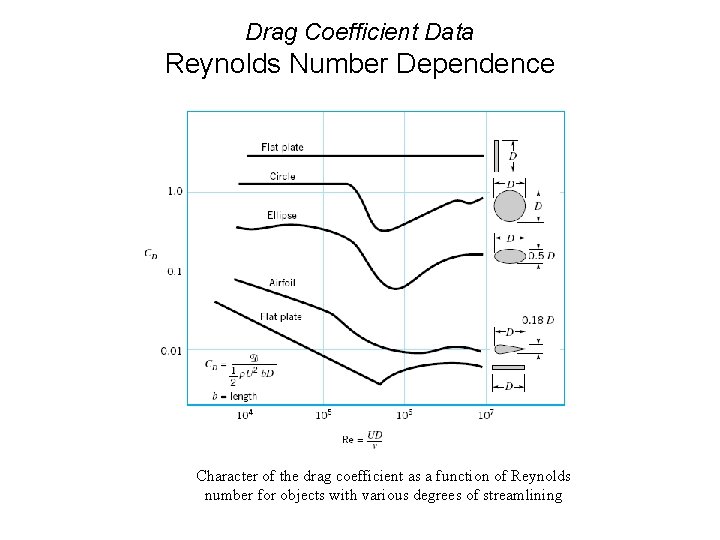
Drag Coefficient Data Reynolds Number Dependence Character of the drag coefficient as a function of Reynolds number for objects with various degrees of streamlining

Drag Coefficient Data Compressibility Effects • For large U, compressibility effects become important and CD = (Re, Ma) • Precise dependence of CD on Re and Ma is complex. • Drag coefficient is usually independent of Mach number for Ma < 0. 5. For larger Mach number, CD strongly depend on Ma, with secondary Reynolds number effects. Figure • For most objects values of CD increase dramatically in the vicinity of Ma = 1 due to existence of shock waves Figure • The character of the drag coefficient as a function of Mach number is different for blunt bodies than for sharp bodies Figure

Drag Coefficient Data Surface Roughness • Depending on the body shape, an increase in surface roughness may increase or decrease drag • In general, for streamline bodies (flat plate parallel to flow) drag increases with increasing surface roughness • For extremely blunt body (flat plate normal to flow) drag is independent of surface roughness • For blunt bodies like a circular cylinder or sphere, an increase in surface roughness can cause a decrease in the drag Figure

Drag Coefficient Data Froude Number Effects • Froude number is the ratio of free-stream speed to wave speed on the interface of two fluids. • Object moving on the surface produces waves that require the source of energy. • Drag coefficient for surface ships is a function of Reynolds number (viscous effects) and Froude number (wave-making effects) • Viscous and wave effect can be separated • Wave-making drag Dw is a complex function of the Froude number and the body shape Figure

Drag Coefficient Data Composite Body Drag • Drag on a complex body can be approximated as the sum of the drag on its parts Example • Aerodynamic drag on automobiles provides one more example of the use of composite bodies Figure • Drag coefficient information is available in the literature Figures
Lift

Lift • Lift is given in term of the lift coefficient which is obtained from experiments • CL = (shape, Re, Ma, Fr, /l) • Body shape is the most important parameter that effects the lift coefficient • Relative importance of shear stress and pressure effects depends on Re • For large Re most of the lift comes from pressure forces
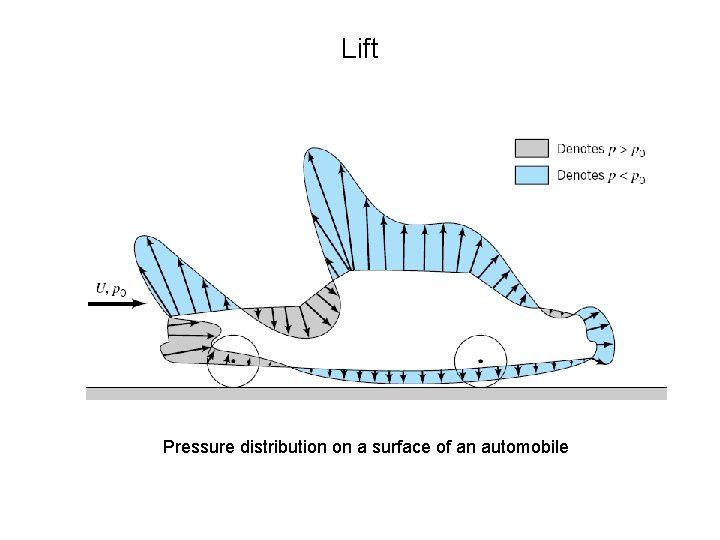
Lift Pressure distribution on a surface of an automobile

Lift • For creeping flows (Re<1) shear stress and pressure effects may be comparable • Airfoils produce lift by generating pressure distribution that is different on the top and bottom surfaces • For large Re pressure distributions are directly proportional to the dynamic pressure, with viscous effects being of secondary importance
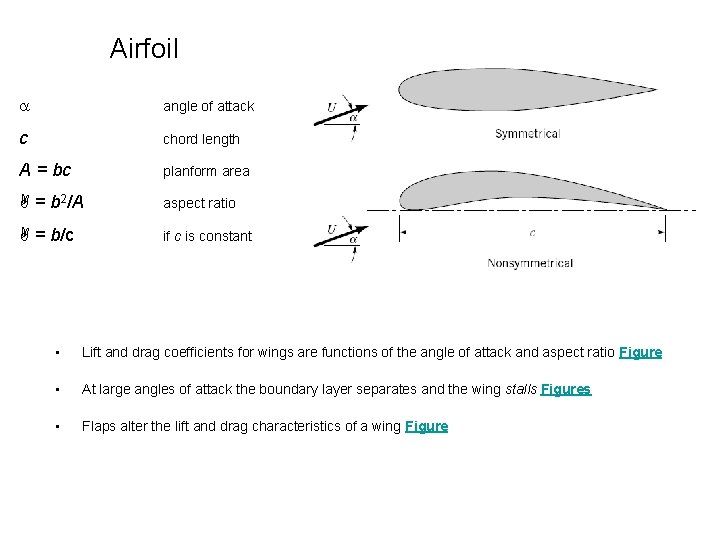
Airfoil angle of attack c chord length A = bc planform area = b 2/A aspect ratio = b/c if c is constant • Lift and drag coefficients for wings are functions of the angle of attack and aspect ratio Figure • At large angles of attack the boundary layer separates and the wing stalls Figures • Flaps alter the lift and drag characteristics of a wing Figure

That’s all
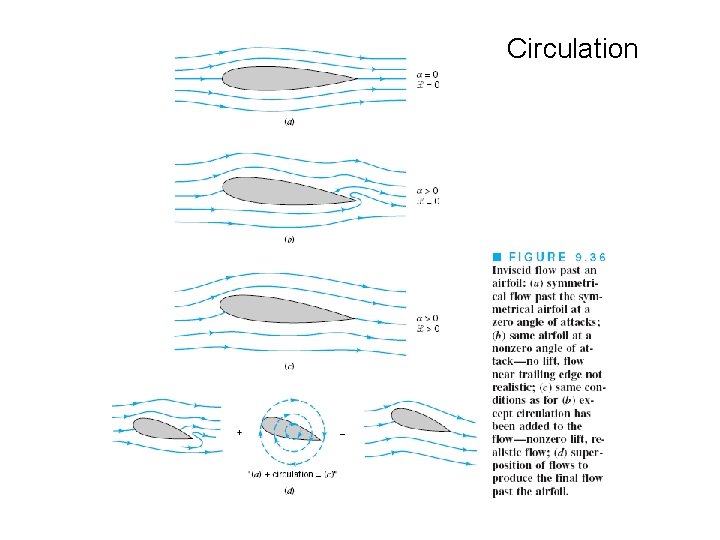
Circulation
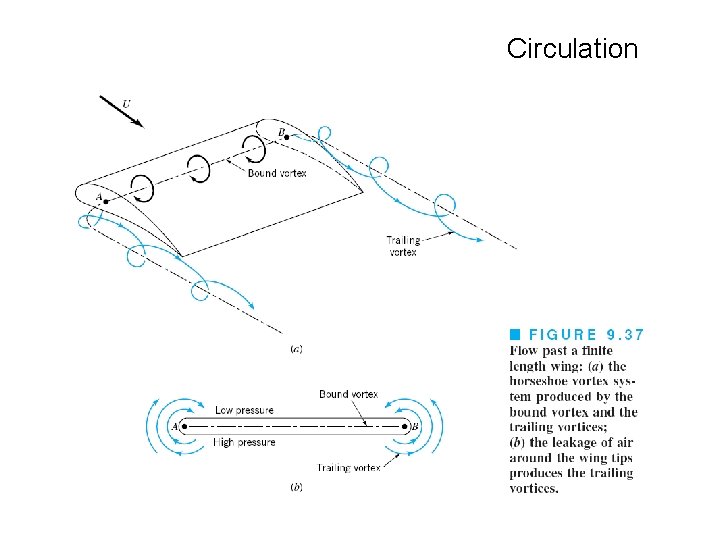
Circulation
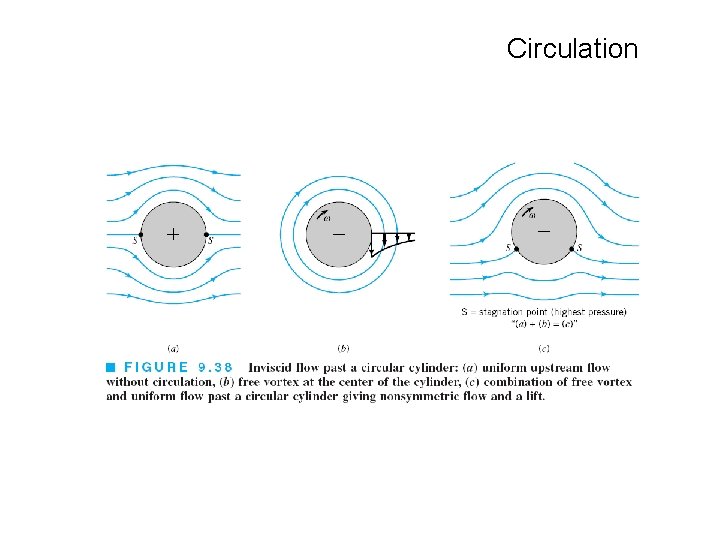
Circulation
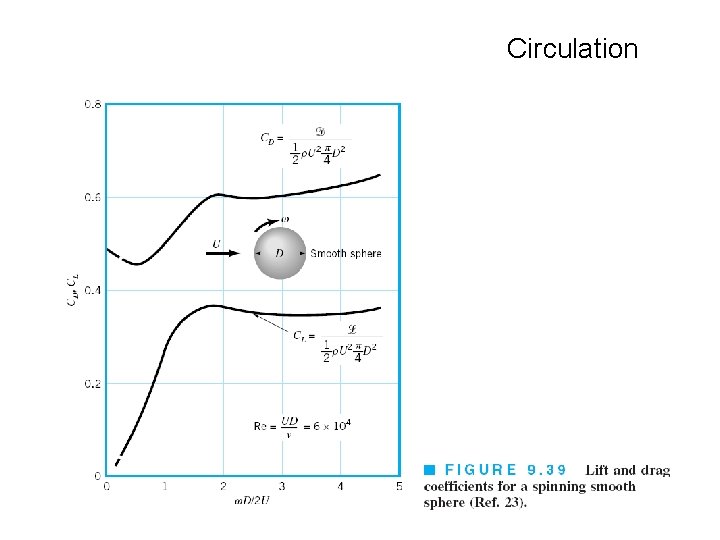
Circulation

Boundary Layer Characteristics Typical characteristics of boundary layer thickness and wall shear stress for laminar and turbulent boundary layers back

Navier-Stokes equations back
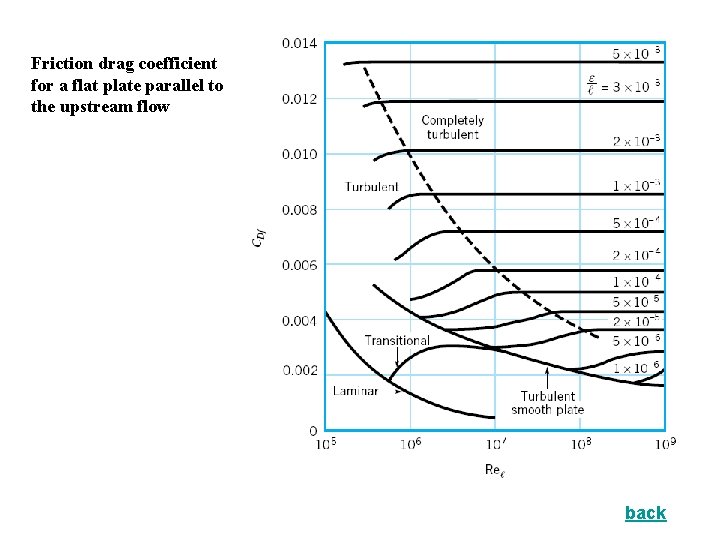
Friction drag coefficient for a flat plate parallel to the upstream flow back

back
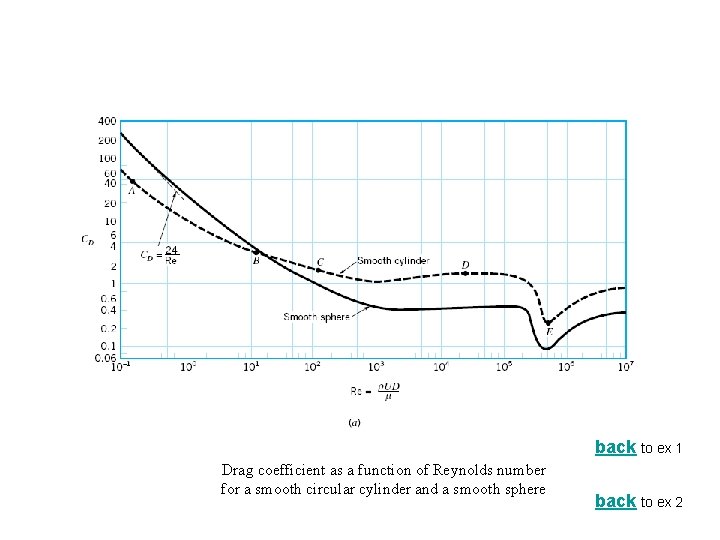
back to ex 1 Drag coefficient as a function of Reynolds number for a smooth circular cylinder and a smooth sphere back to ex 2
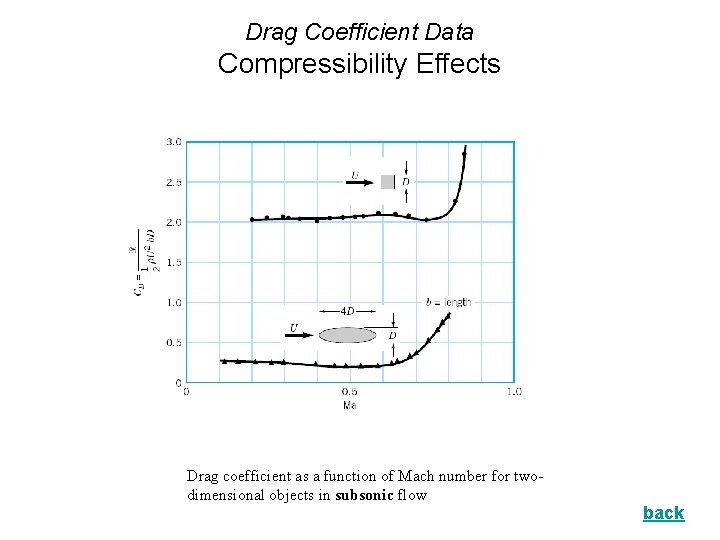
Drag Coefficient Data Compressibility Effects Drag coefficient as a function of Mach number for twodimensional objects in subsonic flow back
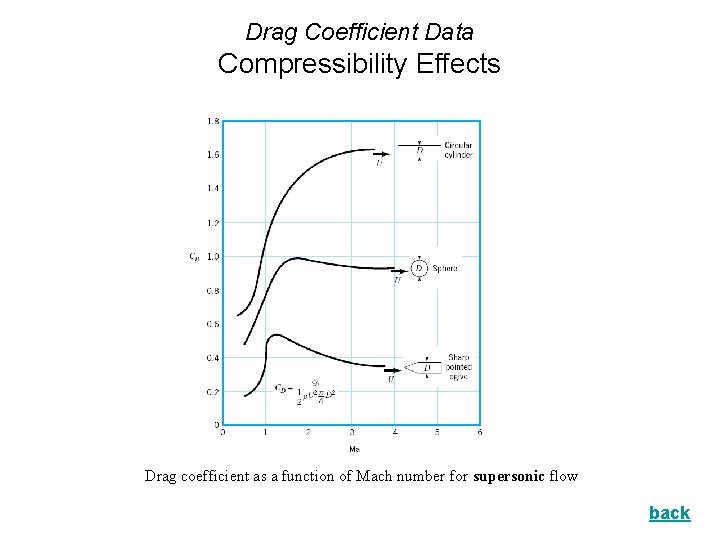
Drag Coefficient Data Compressibility Effects Drag coefficient as a function of Mach number for supersonic flow back
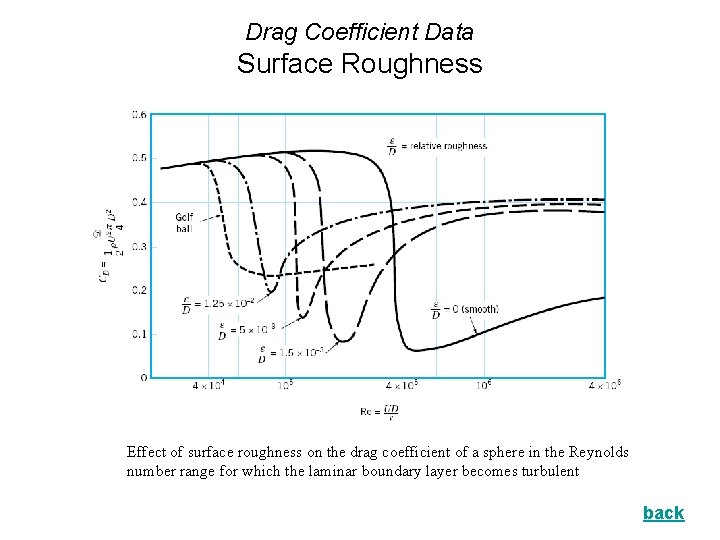
Drag Coefficient Data Surface Roughness Effect of surface roughness on the drag coefficient of a sphere in the Reynolds number range for which the laminar boundary layer becomes turbulent back
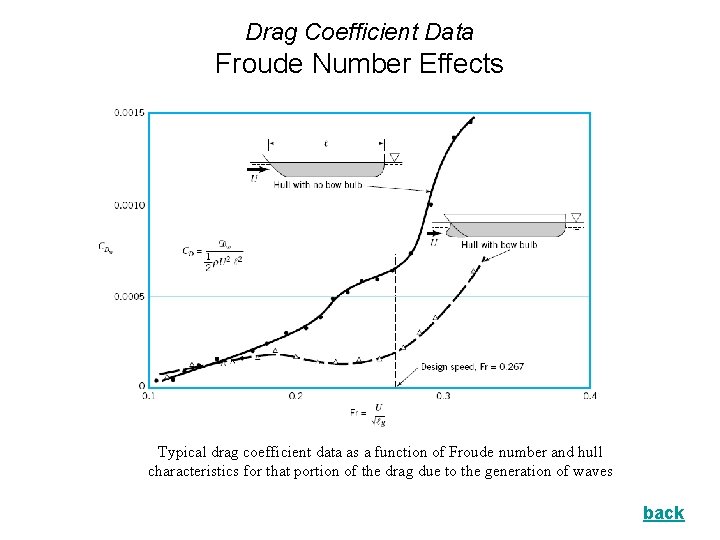
Drag Coefficient Data Froude Number Effects Typical drag coefficient data as a function of Froude number and hull characteristics for that portion of the drag due to the generation of waves back
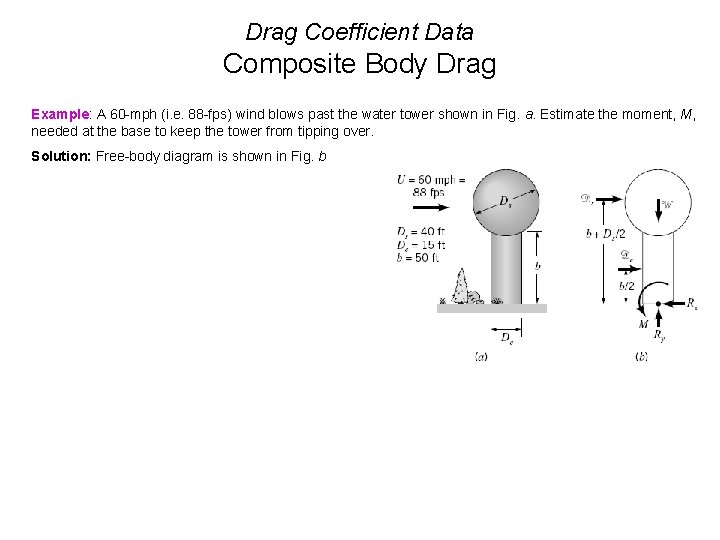
Drag Coefficient Data Composite Body Drag Example: A 60 -mph (i. e. 88 -fps) wind blows past the water tower shown in Fig. a. Estimate the moment, M, needed at the base to keep the tower from tipping over. Solution: Free-body diagram is shown in Fig. b

Drag Coefficient Data Composite Body Drag Example: A 60 -mph (i. e. 88 -fps) wind blows past the water tower shown in Fig. a. Estimate the moment, M, needed at the base to keep the tower from tipping over. Solution: Free-body diagram is shown in Fig. b From Figure 9. 21 Answer:

Example: (cntd. ) Comments: Above result is only an estimate because (a) wind is not uniform (b) tower is not exactly combination of smooth sphere and circular cylinder (c) cylinder is not of infinite length (d) due to interaction of cylinder and sphere the net drag is not the sum of the two (e) drag coefficient was obtained by extrapolation back
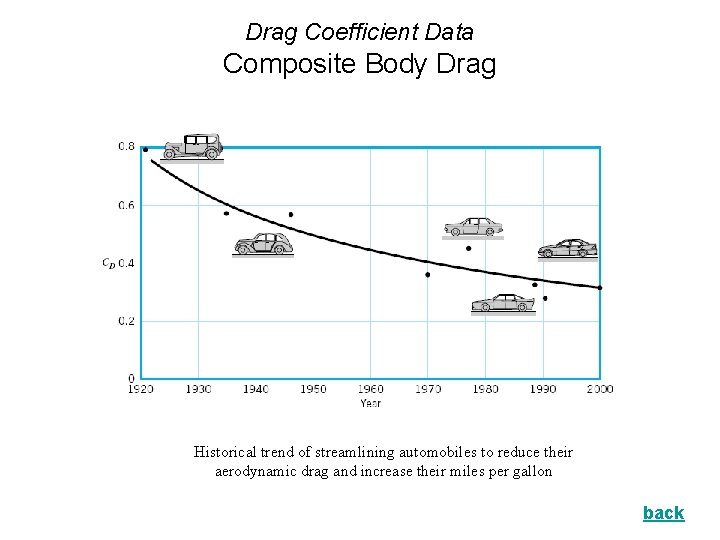
Drag Coefficient Data Composite Body Drag Historical trend of streamlining automobiles to reduce their aerodynamic drag and increase their miles per gallon back
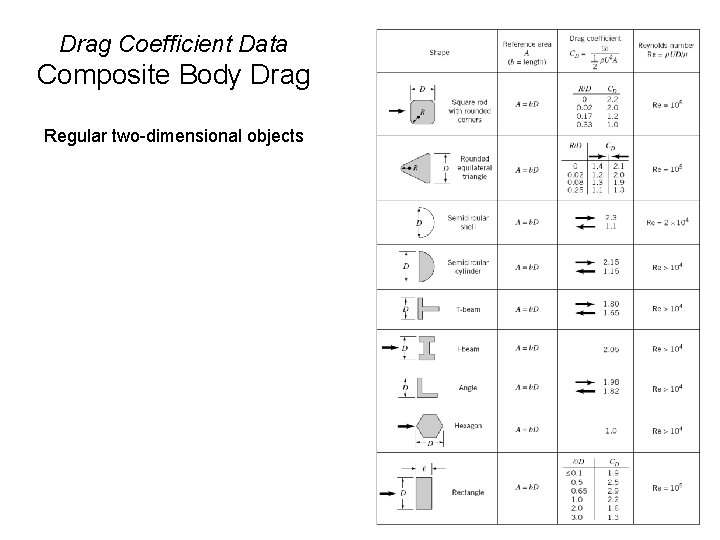
Drag Coefficient Data Composite Body Drag Regular two-dimensional objects
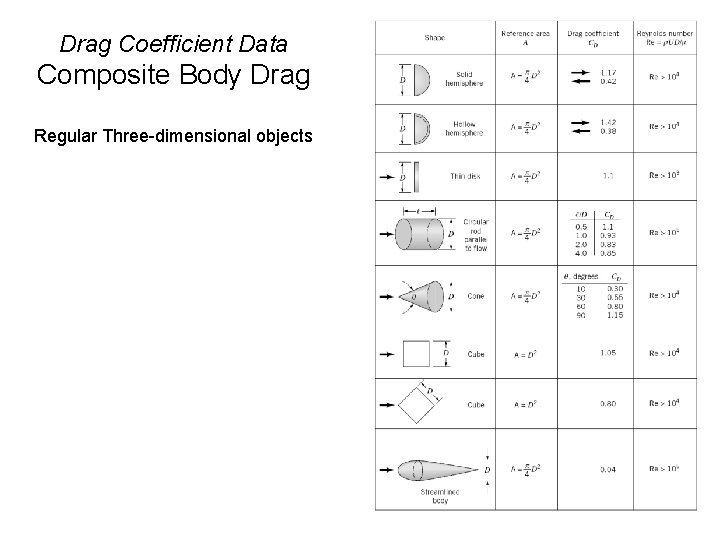
Drag Coefficient Data Composite Body Drag Regular Three-dimensional objects
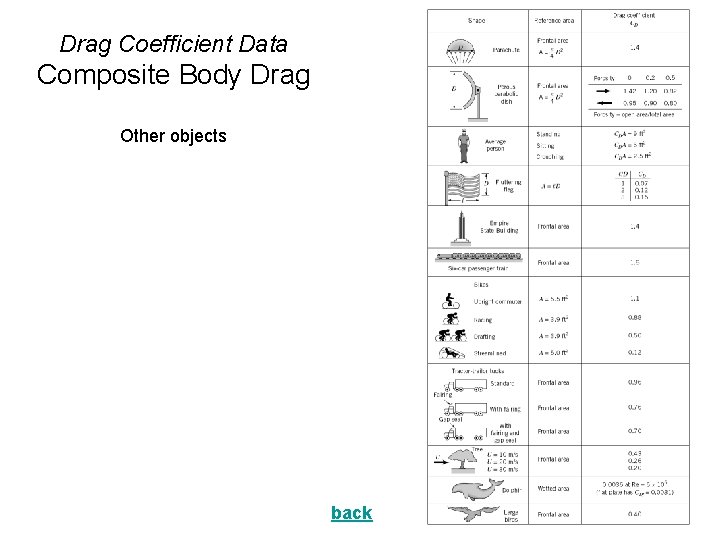
Drag Coefficient Data Composite Body Drag Other objects back
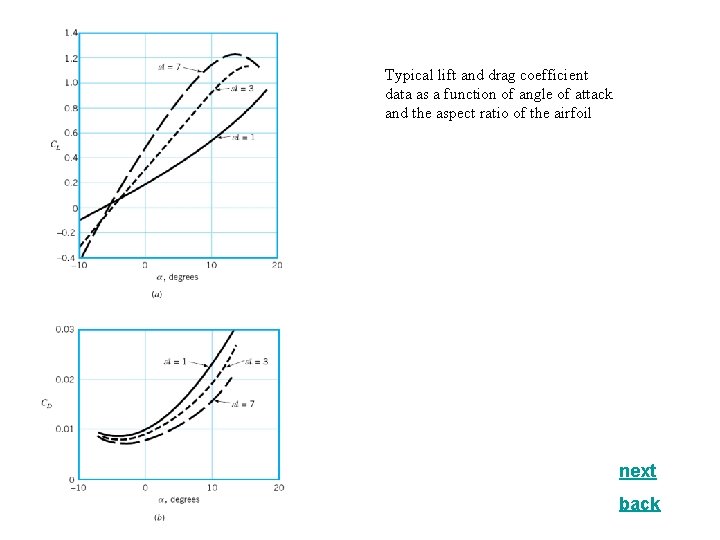
Typical lift and drag coefficient data as a function of angle of attack and the aspect ratio of the airfoil next back
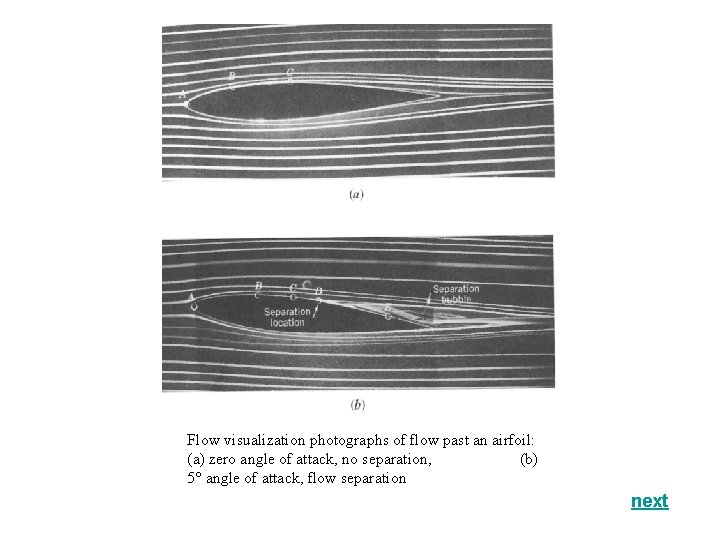
Flow visualization photographs of flow past an airfoil: (a) zero angle of attack, no separation, (b) 5° angle of attack, flow separation next
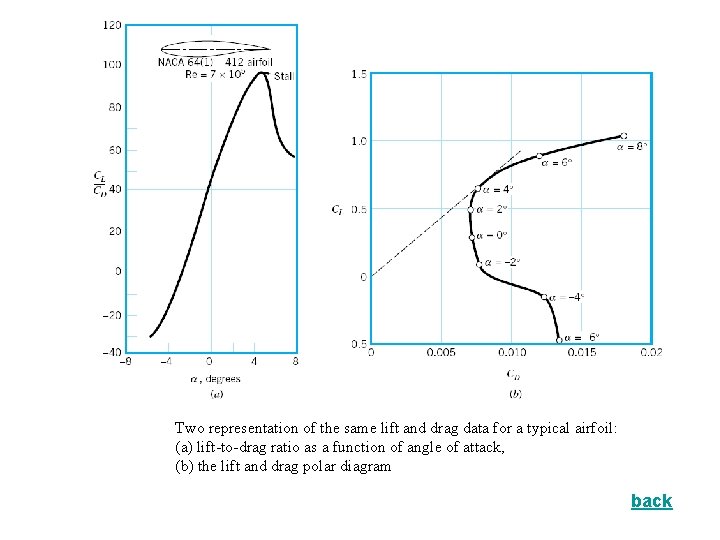
Two representation of the same lift and drag data for a typical airfoil: (a) lift-to-drag ratio as a function of angle of attack, (b) the lift and drag polar diagram back
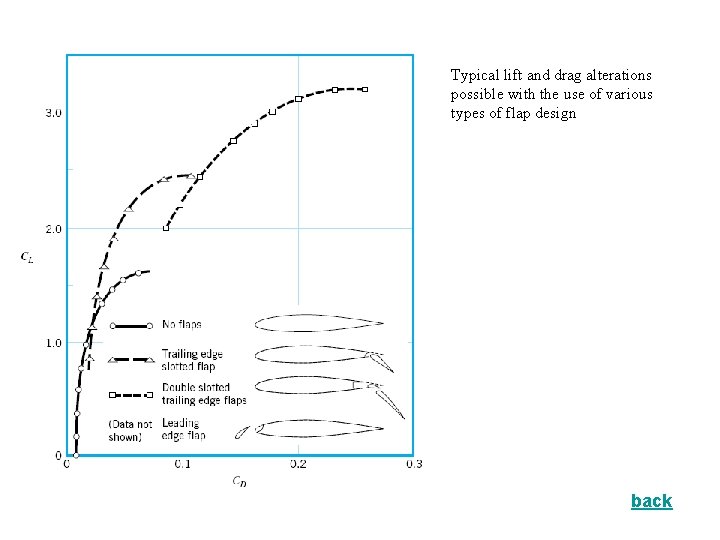
Typical lift and drag alterations possible with the use of various types of flap design back

Momentum-Integral Boundary Layer Method Assume (guess) velocity profile in the boundary layer Obtain equation for from Calculate shear stress from Calculate drag from Even crude guess at the velocity profile gives reasonable drag and shear stress
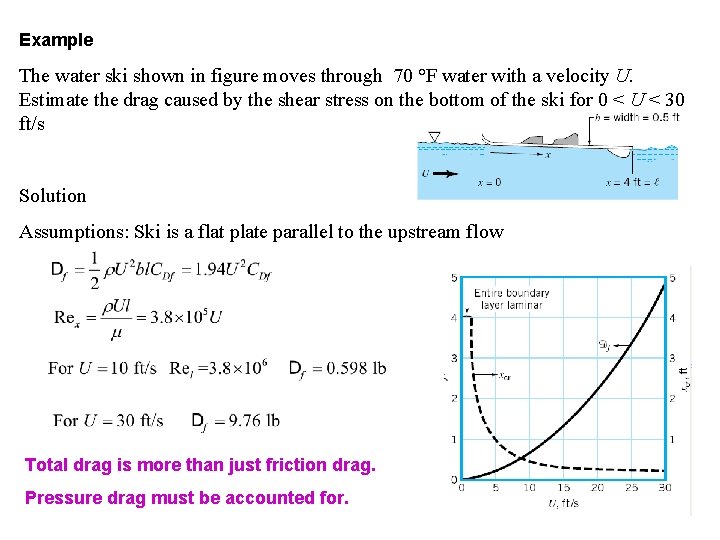
Example The water ski shown in figure moves through 70 °F water with a velocity U. Estimate the drag caused by the shear stress on the bottom of the ski for 0 < U < 30 ft/s Solution Assumptions: Ski is a flat plate parallel to the upstream flow Total drag is more than just friction drag. Pressure drag must be accounted for.

Momentum-Integral Boundary Layer Equation with Nonzero Pressure Gradient Pressure gradient effects can be included in the momentum integral equation Free-stream velocity is not constant along the curved body Total pressure is constant along the streamlines outside the boundary layer Pressure gradient Momentum integral equation with pressure gradient: This equation represents a balance between viscous forces, pressure forces and the fluid momentum
- Slides: 120