Flow Networks ChingChen Huang HsiYue Hsiao CONTENTS n

Flow Networks Ching-Chen Huang Hsi-Yue Hsiao

CONTENTS n Network flows on directed acyclic graphs n Ford-fulkerson Algorithms -Residual networks

Network flows on directed acyclic graphs n n DAG is a directed graph with no cycles. Flow network: a flow network G = (V, E) is a directed graph in which each edge (u, v) ∈ E has a nonnegative capacity c(u, v) >= 0. if (u, v) ∉ E , we assume that c(u, v) = 0. We distinguish two vertices in flow network , source s and sink t. The source produces the material at a steady rate. The sink consumes the material at a steady rate. Objective : how much of material can be imposed through the network that it can handle.

n n n Flow: A flow in G is a real-valued function f : V × V → R that satisfies three properties: 1. Capacity constraint : For all u, v ∈ V, we require f(u, v) ≤ c(u, v). The net flow from one vertex to another must not exceed the given capacity. n 2. Skew symmetry : For all u, v ∈ V, we require f(u, v) = -f(v, u). The net flow from a vertex u to a vertex v is the negative of the net flow in the n 3. Flow conservation : For all u ∈ V - {s, t}, we require ∑ f(u, v) = 0. n v∈V The quantity f(u, v), which can be positive or negative , is called the net flow from vertex u to v. The value of the flow is defined as | f | = ∑ f(s, v) that is the totat net v∈V Flow out of the source.

Residual Capacity n n n Given a flow f in network G = (V, E). Consider a pair of vertices u, v ∈ V. Residual capacity: ¨ The amount of additional flow we can push directly from u to v. ¨ cf (u, v) = c(u, v) f (u, v) ≥ 0 (since f (u, v) ≤ c(u, v)) n Example: ¨ c(u, v) = 16, f(u, v) = 5 cf (u, v) = 11

Residual Network Residual network: Gf = (V, Ef ), Ef = {(u, v) ∈ V × V : cf (u, v) > 0}. n Each edge of the residual network can admit a positive flow. n Given flows f 1 and f 2, the flow sum f 1 + f 2 is n ¨ (f 1 + f 2)(u, v) = f 1(u, v) + f 2(u, v) for all u, v ∈ V.

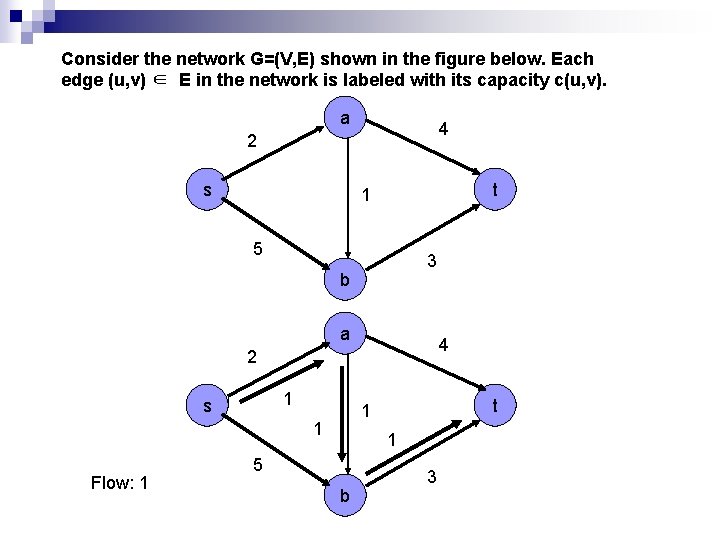
Consider the network G=(V, E) shown in the figure below. Each edge (u, v) ∈ E in the network is labeled with its capacity c(u, v). a 4 2 s t 1 5 3 b a 4 2 1 s 1 Flow: 1 t 1 1 5 b 3

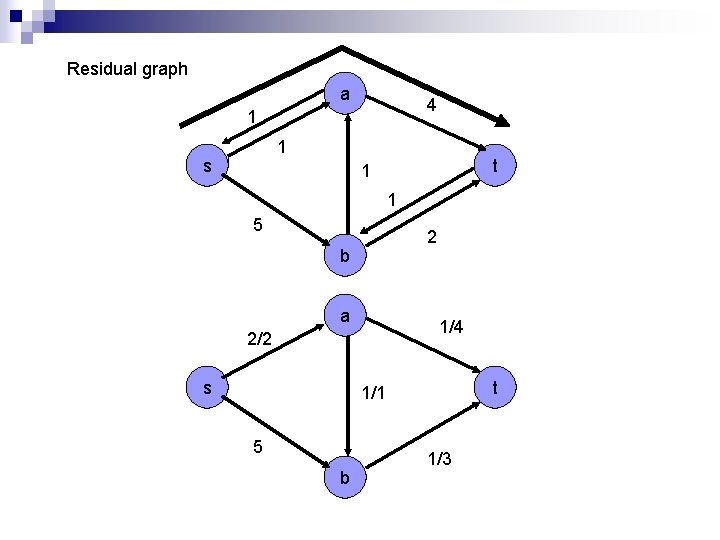
Residual graph a 4 1 1 s t 1 1 5 2 b a 1/4 2/2 s t 1/1 5 b 1/3

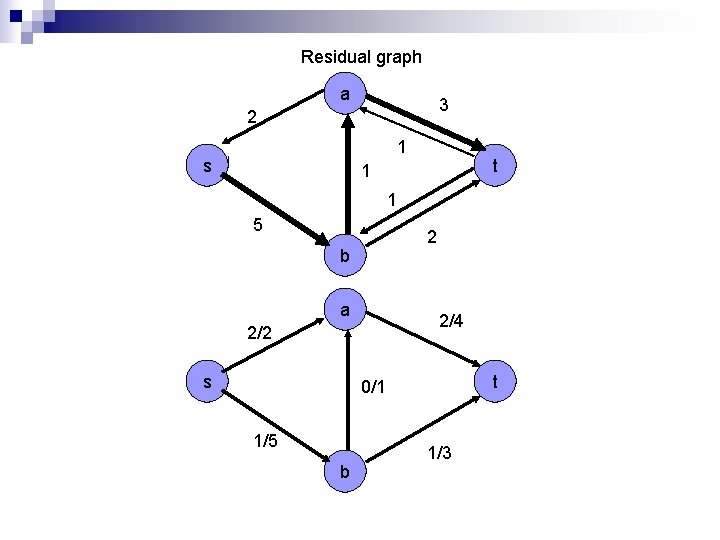
Residual graph a 3 2 1 s t 1 1 5 2 b a 2/4 2/2 s t 0/1 1/5 b 1/3

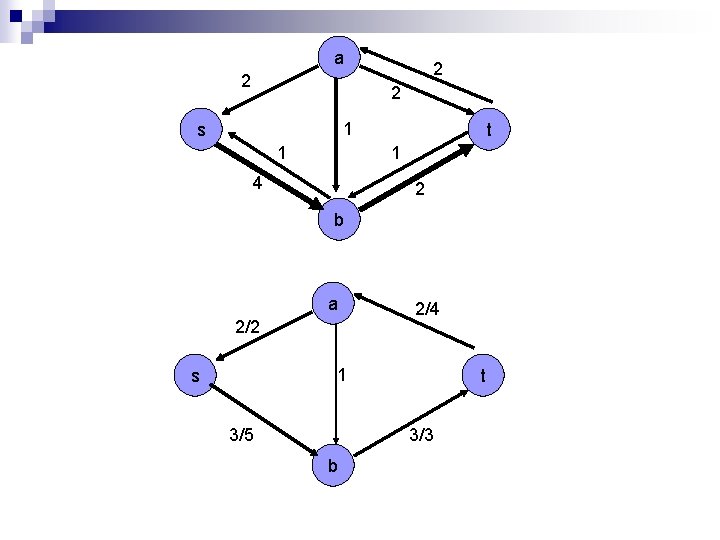
a 2 2 2 1 s 1 t 1 4 2 b a 2/2 2/4 1 s 3/5 t 3/3 b

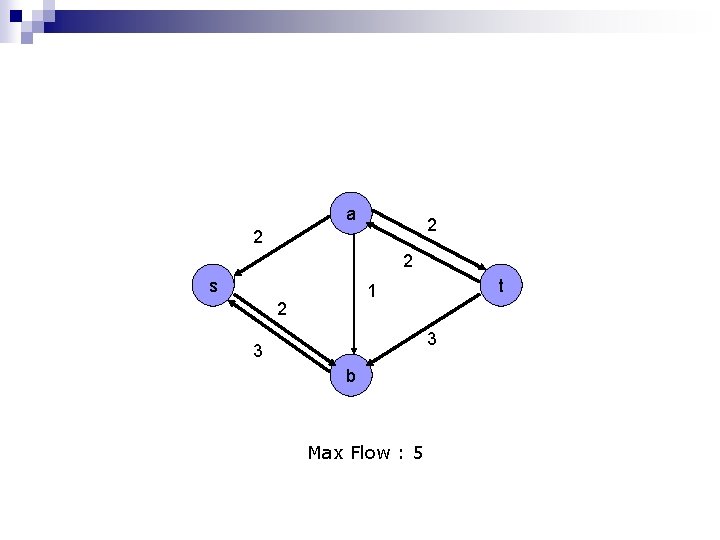
a 2 2 2 s t 1 2 3 3 b Max Flow : 5

Ford-Fulkerson Algorithm n The Ford_Fulkerson method is iterative, n Starts with f(u, v) for (u, v) ∈ V, initial flow of value 0. n The method is based on the augmenting path which is n defined as a path from s to t along which we can push n more flow and then augment flow along this path.

n Procedure Ford_Fulkerson_method(G, s, t): For each edge (u, v) ∈ E[G] do f[u, v] 0 f[v, u] 0 While there exists a path p from s to t in the residual network G 1 do c 1(p) min{ c 1(u, v): (u, v) is in p} for each edge (u, v) in p do f[u, v] + c 1(p) f[u, v] -f[u, v]

n Running time for this algorithms is O(E * |f*|) where f* is the maximum flow found by algorithm. n First three Lines take time θ(E). n The while loop of last five lines is executed at most |f*| times, since the flow value increases by at least one unit in each iteration.

Ford-Fulkerson Algorithm Ford-Fulkerson(G, s, t) ; G = (V, E) 1 for each edge (u, v) in E 2 f(u, v) = f(v, u) = 0 3 while exists path p from s to t in residual network Gf 4 do cf (p) = min{cf (u, v) : (u, v) is in p} 5 for each edge (u, v) on p 6 f(u, v) = f(u, v) + cf (p) 7 f(v, u) = -f(u, v)

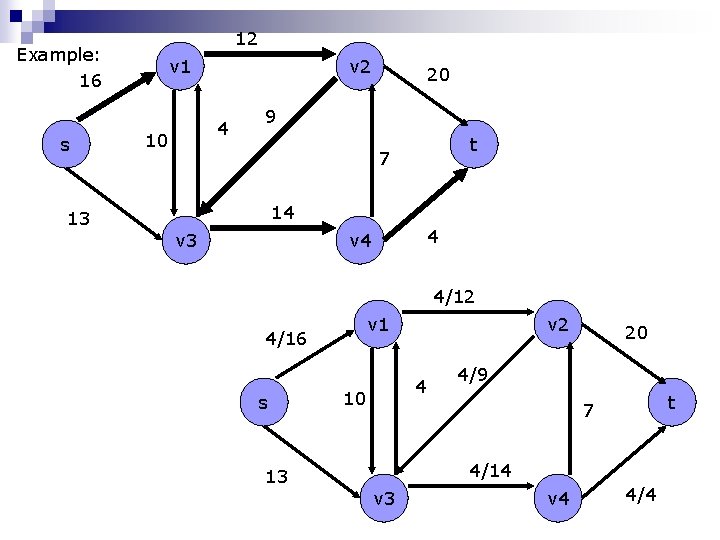
12 Example: 16 s 13 v 1 v 2 4 10 20 9 t 7 14 v 3 4 v 4 4/12 v 1 4/16 s 13 v 2 4 10 20 4/9 t 7 4/14 v 3 v 4 4/4

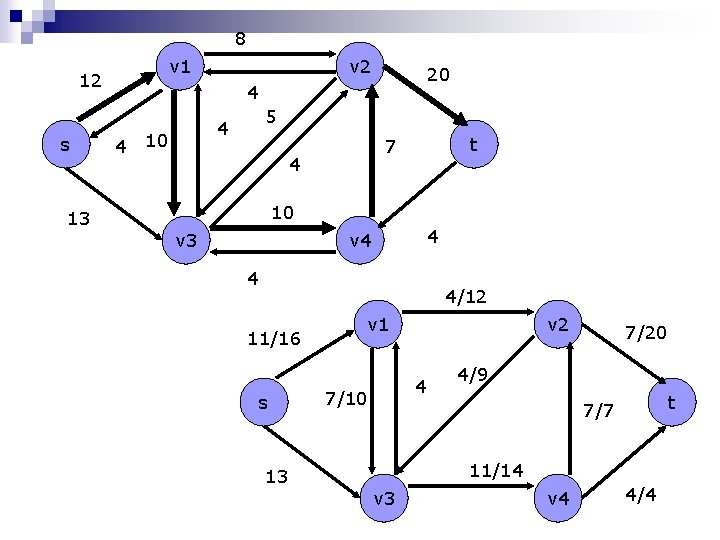
8 v 1 12 s 13 v 2 20 4 4 5 4 10 t 7 4 10 v 3 4 v 4 4 4/12 11/16 s 13 v 1 v 2 4 7/10 7/20 4/9 t 7/7 11/14 v 3 v 4 4/4

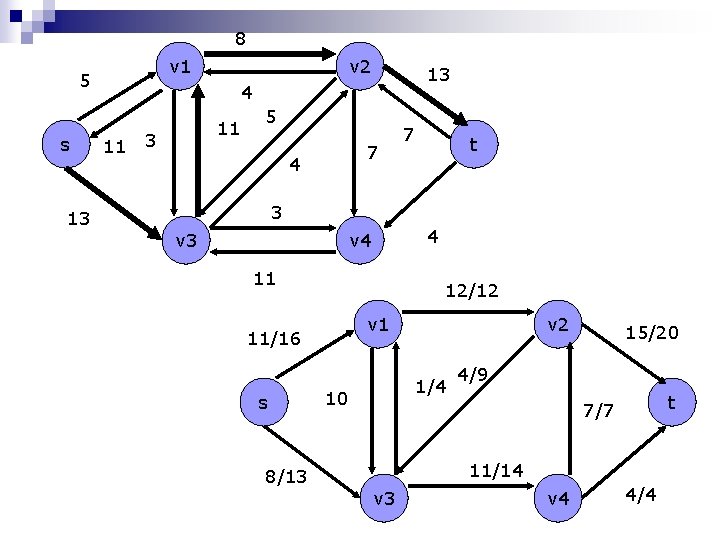
8 v 1 5 s 13 v 2 13 4 11 11 3 5 7 4 7 t 3 v 3 4 v 4 11 12/12 v 1 11/16 s 8/13 v 2 1/4 10 15/20 4/9 t 7/7 11/14 v 3 v 4 4/4

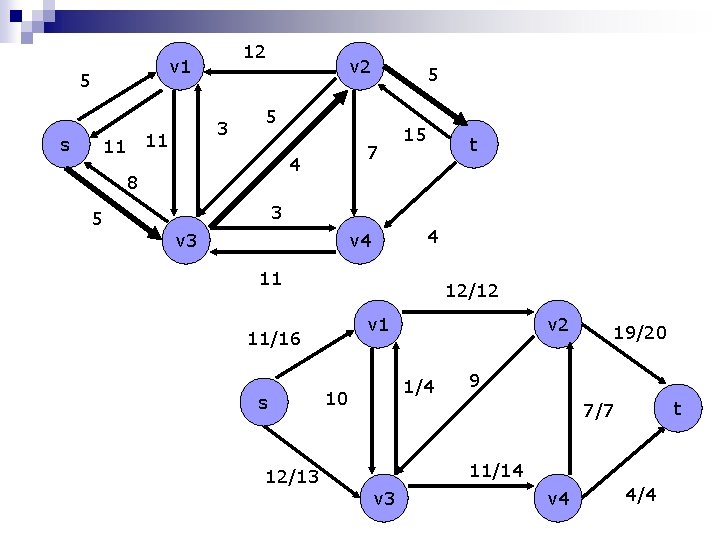
12 v 1 5 s 3 11 11 v 2 5 7 4 8 5 5 15 t 3 v 3 4 v 4 11 12/12 v 1 11/16 s 12/13 v 2 1/4 10 19/20 9 t 7/7 11/14 v 3 v 4 4/4

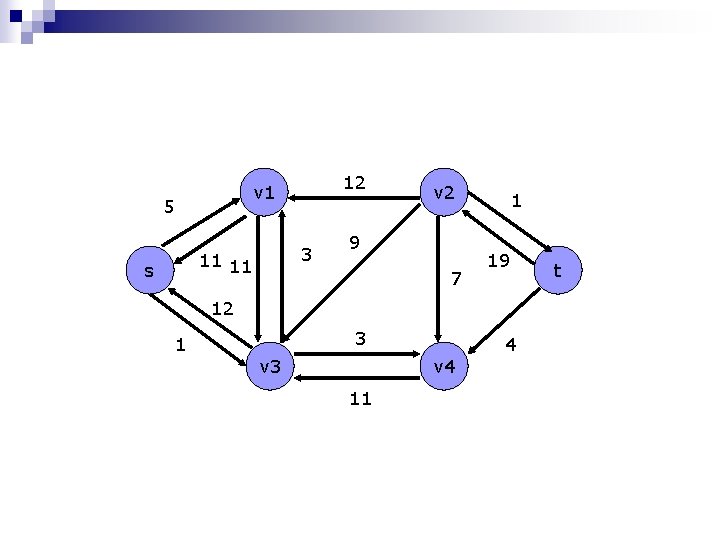
12 v 1 5 3 11 11 s v 2 9 7 1 19 12 1 3 v 4 11 4 t

Reference Class Notes from Dr. Istvan Jonyer of Oklahoma State University n Class Notes from CSE 5311 of 2004, made by Hiren Patel, Ujjval Patel n