FLOW NETS Techniques for Finding Solutions to Groundwater



























- Slides: 30

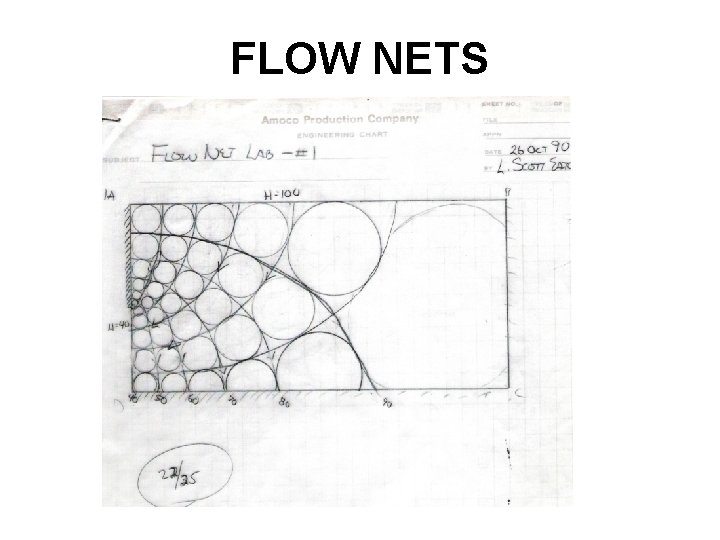
FLOW NETS

Techniques for Finding “Solutions” to Groundwater Flow”

Techniques for Finding “Solutions” to Groundwater Flow” • Inspection (intuition) • Graphical Techniques

Techniques for Finding “Solutions” to Groundwater Flow” • Inspection (intuition) • Graphical Techniques • Analog Models

Techniques for Finding “Solutions” to Groundwater Flow” • • Inspection (intuition) Graphical Techniques Analog Models Analytical Mathematical Techniques (Calculus)

Techniques for Finding “Solutions” to Groundwater Flow” • • • Inspection (intuition) Graphical Techniques Analog Models Analytical Mathematical Techniques (Calculus) Numerical Mathematical Techniques (Computers)

I. Introduction A. Overview

I. Introduction A. Overview • one of the most powerful tools for the analysis of groundwater flow.

I. Introduction A. Overview • one of the most powerful tools for the analysis of groundwater flow. • provides a solution to La. Places Equation for 2 -D, steady state, boundary value problem.

I. Introduction A. Overview • one of the most powerful tools for the analysis of groundwater flow. • provides a solution to La. Places Equation for 2 -D, steady state, boundary value problem. • To solve, need to know:

I. Introduction A. Overview • one of the most powerful tools for the analysis of groundwater flow. • provides a solution to La. Places Equation for 2 -D, steady state, boundary value problem. • To solve, need to know: – have knowledge of the region of flow

I. Introduction A. Overview • one of the most powerful tools for the analysis of groundwater flow. • provides a solution to La. Places Equation for 2 -D, steady state, boundary value problem. • To solve, need to know: – – have knowledge of the region of flow boundary conditions along the perimeter of the region

• To solve, need to know: – – – have knowledge of the region of flow boundary conditions along the perimeter of the region spatial distribution of hydraulic head in region.

• Composed of 2 sets of lines – – equipotential lines (connect points of equal hydraulic head) flow lines (pathways of water as it moves through the aquifer.

• Composed of 2 sets of lines – – d 2 h dx 2 equipotential lines (connect points of equal hydraulic head) flow lines (pathways of water as it moves through the aquifer. + d 2 h = dy 2 0 gives the rate of change of h in 2 dimensions

II. Assumptions Needed For Flow Net Construction

II. • • Assumptions Needed For Flow Net Construction Aquifer is homogeneous, isotropic Aquifer is saturated

II. • • • Assumptions Needed For Flow Net Construction Aquifer is homogeneous, isotropic Aquifer is saturated There is no change in head with time

II. • • Assumptions Needed For Flow Net Construction Aquifer is homogeneous, isotropic Aquifer is saturated There is no change in head with time Soil and water are incompressible

II. • • • Assumptions Needed For Flow Net Construction Aquifer is homogeneous, isotropic Aquifer is saturated there is no change in head with time soil and water are incompressible Flow is laminar, and Darcys Law is valid

II. • • • Assumptions Needed For Flow Net Construction Aquifer is homogeneous, isotropic Aquifer is saturated there is no change in head with time soil and water are incompressible flow is laminar, and Darcys Law is valid All boundary conditions are known.

III. Boundaries

III. Boundaries A. Types

III. Boundaries A. Types 1. Impermeable 2. Constant Head 3. Water Table

III. Boundaries A. Types 1. Impermeable 2. Constant Head 3. Water Table

III. Boundaries B. Calculating Discharge Using Flow Nets Q’ = Kph f Where: Q’ = Discharge per unit depth of flow net (L 3/t/L) K = Hydraulic Conductivity (L/t) p = number of flow tubes h = head loss (L) f = number of equipotential drops

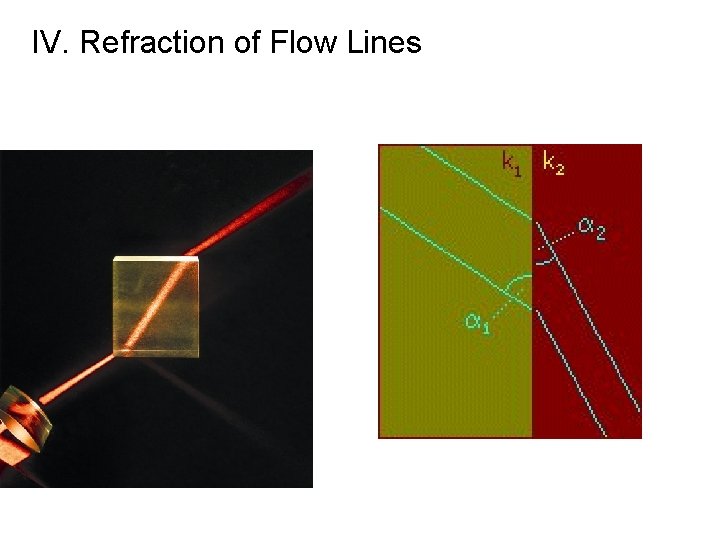
IV. Refraction of Flow Lines

IV. Refraction of Flow Lines A. The derivation B. The general relationships C. An example problem

IV. Flow Nets: Isotropic, Heterogeneous Types A. “Reminder” of the conditions needed to draw a flow net for homogeneous, isotropic conditions B. An Example of Iso, Hetero
