Flow Nets Graphical representation of the steadystate velocity










- Slides: 12

Flow Nets • Graphical representation of the steady-state velocity potential and stream function. – Used to determine flow velocities, flow paths, and travel times. • Approach is general and can be applied to a variety of fluid problems including compressible, and incompressible ideal flows. • In porous media, the velocity potential is related to the head and the stream function is related to the path. 1

Velocity Potential • The velocity potential is given by the head or fluid pressure. • The gradient of the velocity potential function is used to recover the velocity value at a point in the flow field. • The velocity potential satisfies the governing mass balance equation for steady-incompressible flow. 2

Streamline • A streamline is defined as a line that is tangent to the velocity vector in a flow field. y u v dy dx streamline x • Tangent means: 3

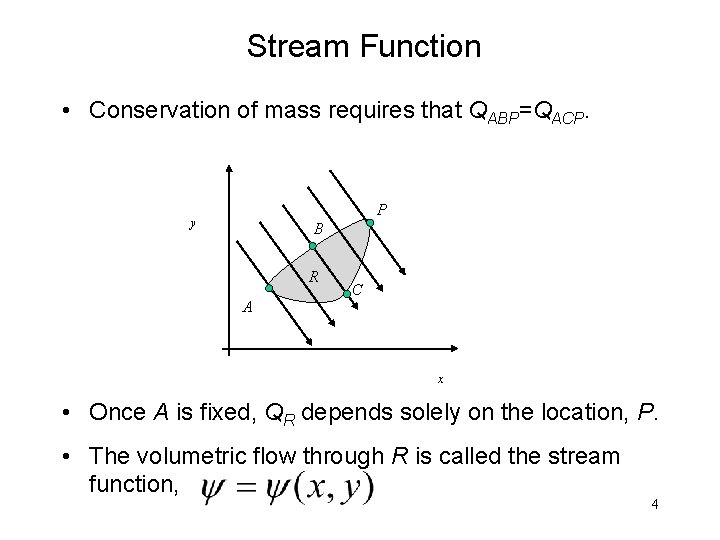
Stream Function • Conservation of mass requires that QABP=QACP. P y B R A C x • Once A is fixed, QR depends solely on the location, P. • The volumetric flow through R is called the stream function, 4

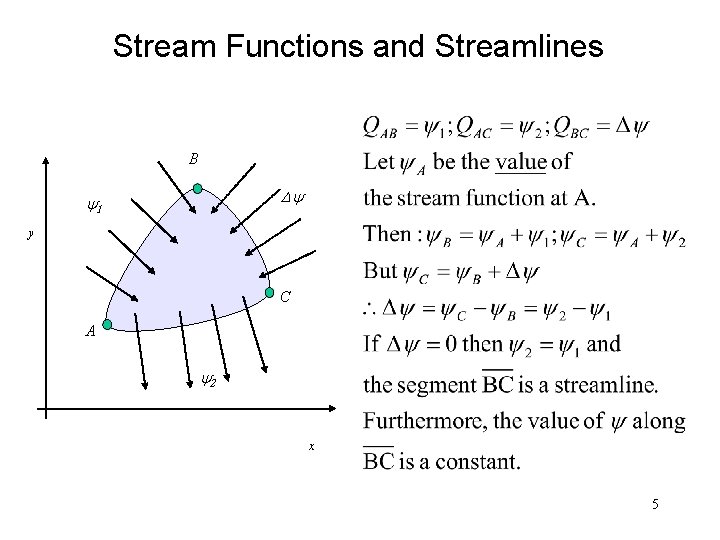
Stream Functions and Streamlines B Dy y 1 y C A y 2 x 5

Potential and Stream Function Relationships • (1) The velocity is given by the gradient of the velocity potential. • (2) Streamlines are tangent to velocity. • (3) Lines of constant y are streamlines. 6

Flow Net Mathematics • The last two relations supply the rules to construct a flow net. • Since both equations equal the same constant, then the partial derivatives in each term must be equal. 7

Cauchy-Riemann Conditions • These equalities are called the Cauchy-Riemann Conditions for Ideal Flow. They are further expanded using Darcy’s Law as: • Or: 8

Streamtubes • Flow bounded by two streamlines is called a streamtube. Y 1 P 1 y DQ Y 2 P 2 A x • Discharge in a streamtube is the difference in the values of the bounding stream functions. 9

Irrotational Flow • Irrotational flow means that: • Substitute Cauchy-Reimann conditions to obtain • Or, in compact notation: 10

Results • Compare to the steady groundwater flow equation. • These two PDEs are the basis of numerical generation of flow nets. 11

Application • Numerical generation of flow nets is accomplished by – Generating discrete distributions of potential and stream functions over the entire problem domain – Contouring the results to create a picture of the flow net. • Practical aspects: – Both governing PDEs are La. Place equations. Thus a tool that solves La. Place problems will suffice for both equations (although boundary conditions will be different) 12
 Steady state error in control system
Steady state error in control system Control system type 0 1 2
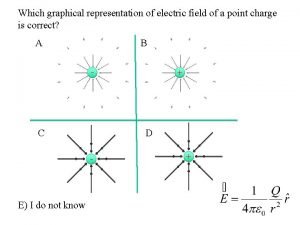
Control system type 0 1 2 It provides a graphical representation of an electric field
It provides a graphical representation of an electric field Ellingham diagram is a graphical representation of
Ellingham diagram is a graphical representation of Hyetograph
Hyetograph Boyle's law graphical representation
Boyle's law graphical representation Is a graphical representation of an algorithm
Is a graphical representation of an algorithm A histogram is a graphical representation of the:
A histogram is a graphical representation of the: Graphical representation
Graphical representation Maximum speed of simple harmonic oscillator
Maximum speed of simple harmonic oscillator Graphical representation of shm
Graphical representation of shm Limit of economic haul
Limit of economic haul Third angle projection method
Third angle projection method