FloatingPoint Reuse in an FPGA Implementation of a

Floating-Point Reuse in an FPGA Implementation of a Ray-Triangle Intersection Algorithm Craig Ulmer cdulmer@sandia. gov June 27, 2006 Adrian Javelo Craig Ulmer UCLA Sandia National Laboratories/CA Sandia is a multiprogram laboratory operated by Sandia Corporation, a Lockheed Martin Company, for the United States Department of Energy’s National Nuclear Security Administration under contract DE-AC 04 -94 AL 85000.

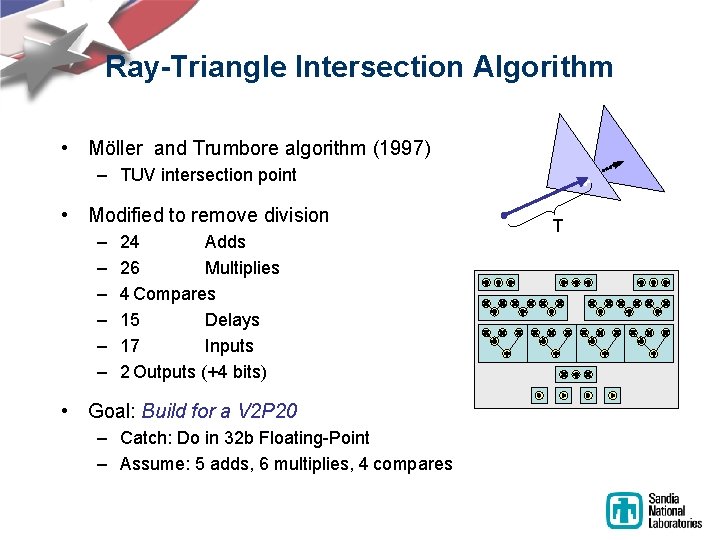
Ray-Triangle Intersection Algorithm • Möller and Trumbore algorithm (1997) – TUV intersection point • Modified to remove division – – – 24 Adds 26 Multiplies 4 Compares 15 Delays 17 Inputs 2 Outputs (+4 bits) • Goal: Build for a V 2 P 20 – Catch: Do in 32 b Floating-Point – Assume: 5 adds, 6 multiplies, 4 compares + T

Outline • Overview – Reusing floating-point hardware • Adapting the Algorithm – Operation Scheduling – Mapping Operations to Units – Intermediate Data Values • Performance Observations – Ongoing Work: Automation • Summary

Floating-Point and FPGAs • Floating-Point has been weakness for FPGA • Recent high-quality FP libraries – SNL: Keith Underwood & K. Scott Hemmert – USC, ENS Lyon, Nallatech, SRC, Xilinx • FP units still challenging to work with – Deeply pipelined – Require sizable resources Single-Precision Function Stages Max in V 2 P 20 Add 10 14 Multiply 11 18 Multiply (no denormals) 6 22 Divide 31 4

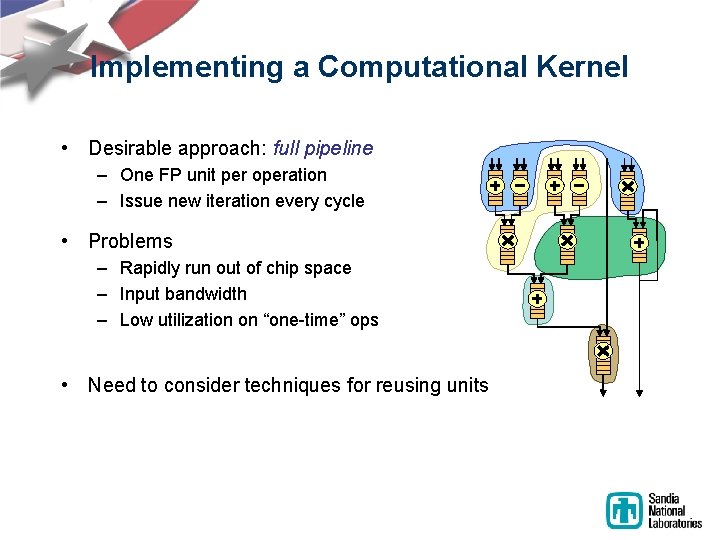
Implementing a Computational Kernel • Desirable approach: full pipeline – One FP unit per operation – Issue new iteration every cycle • Problems – Rapidly run out of chip space – Input bandwidth – Low utilization on “one-time” ops • Need to consider techniques for reusing units

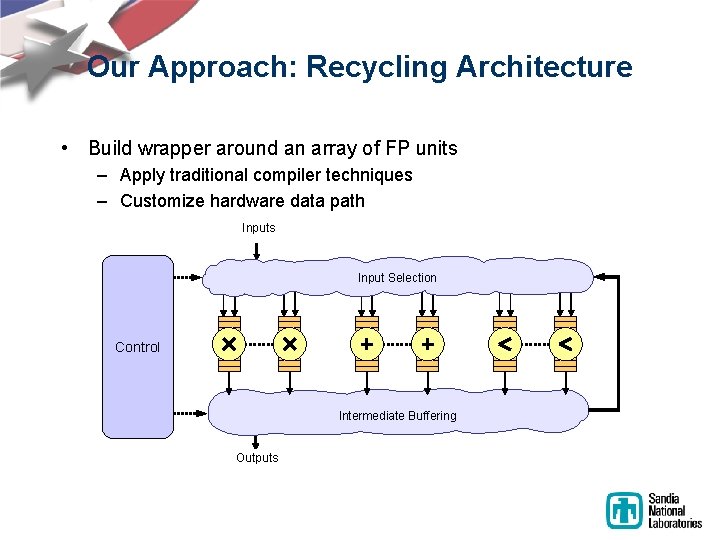
Our Approach: Recycling Architecture • Build wrapper around an array of FP units – Apply traditional compiler techniques – Customize hardware data path Inputs Input Selection Control Intermediate Buffering Outputs

Outline • Overview – Reusing floating-point hardware • Adapting the Algorithm – Operation Scheduling – Mapping Operations to Units – Intermediate Data Values • Performance Observations – Ongoing Work: Automation • Summary

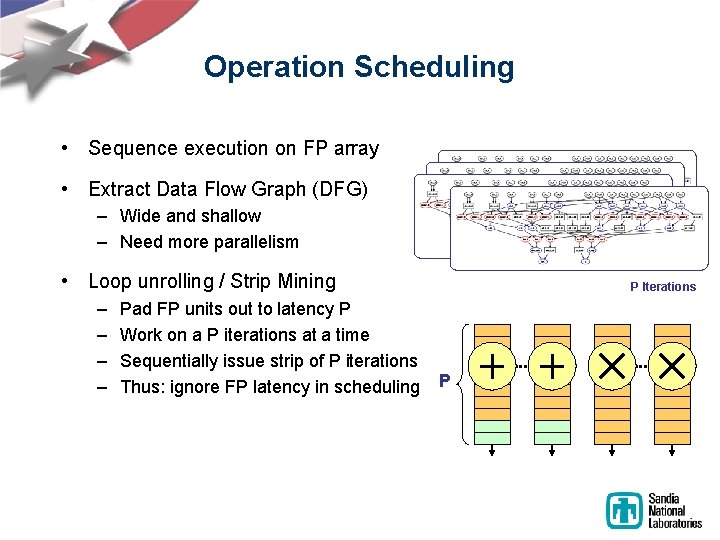
Operation Scheduling • Sequence execution on FP array • Extract Data Flow Graph (DFG) – Wide and shallow – Need more parallelism • Loop unrolling / Strip Mining – – Pad FP units out to latency P Work on a P iterations at a time Sequentially issue strip of P iterations Thus: ignore FP latency in scheduling P Iterations P

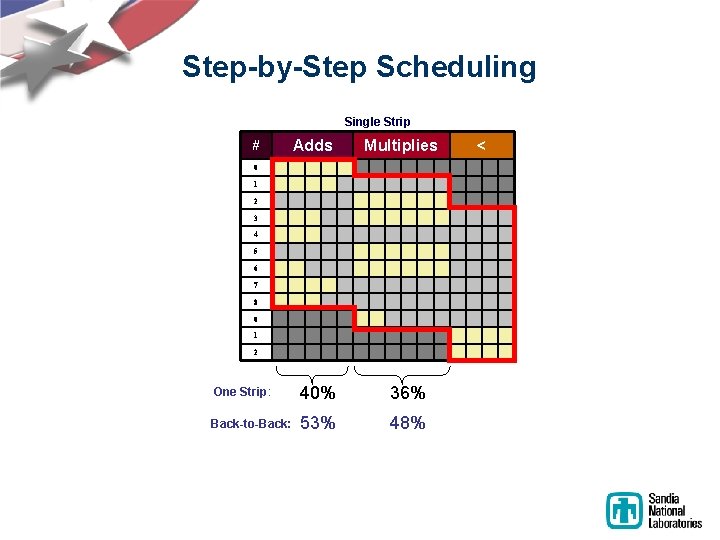
Step-by-Step Scheduling Single Strip # Adds Multiplies 0 1 2 3 4 5 6 7 8 0 1 2 One Strip: 40% 36% Back-to-Back: 53% 48% <

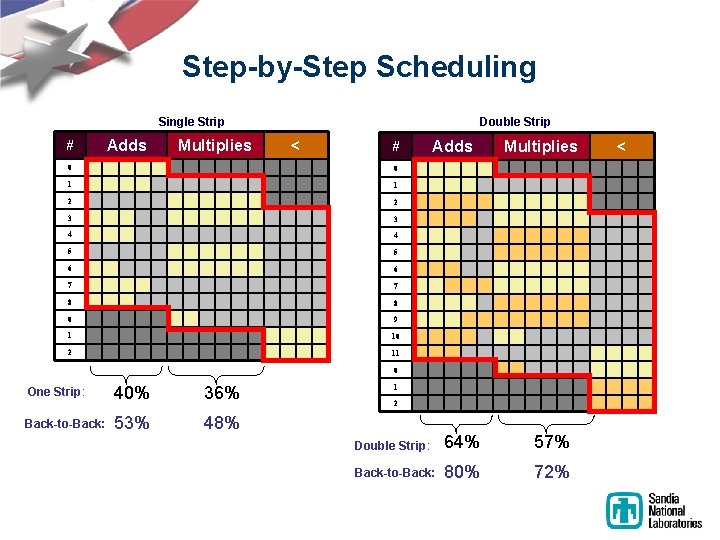
Step-by-Step Scheduling Single Strip # Adds Multiplies Double Strip < # 0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 0 9 1 10 2 11 Adds Multiplies 0 One Strip: Back-to-Back: 40% 36% 53% 48% 1 2 Double Strip: 64% 57% Back-to-Back: 80% 72% <

Outline • Overview – Reusing floating-point hardware • Adapting the Algorithm – Operation Scheduling – Mapping Operations to Units – Intermediate Data Values • Performance Observations – Ongoing Work: Automation • Summary

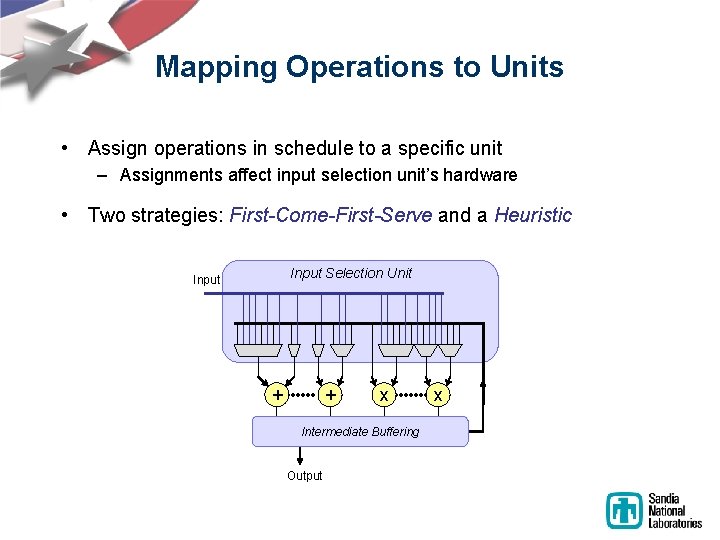
Mapping Operations to Units • Assign operations in schedule to a specific unit – Assignments affect input selection unit’s hardware • Two strategies: First-Come-First-Serve and a Heuristic Input Selection Unit Input + + x Intermediate Buffering Output x

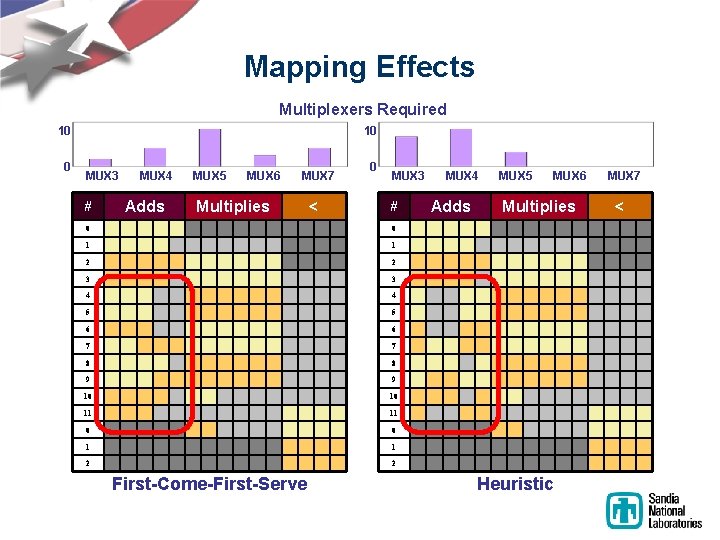
Mapping Effects Multiplexers Required 10 0 10 MUX 3 # MUX 4 Adds MUX 5 MUX 6 MUX 7 Multiplies < 0 MUX 3 # 0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 10 11 11 0 0 1 1 2 2 First-Come-First-Serve MUX 4 Adds MUX 5 MUX 6 Multiplies Heuristic MUX 7 <

Outline • Overview – Reusing floating-point hardware • Adapting the Algorithm – Operation Scheduling – Mapping Operations to Units – Intermediate Data Values • Performance Observations – Ongoing Work: Automation • Summary

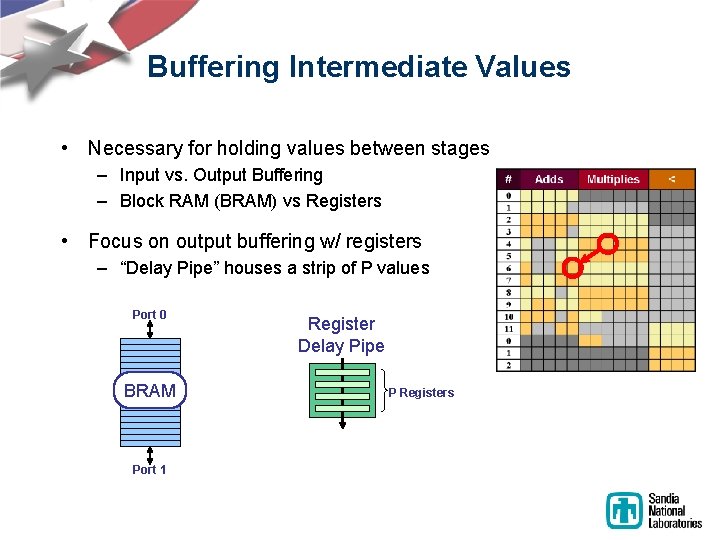
Buffering Intermediate Values • Necessary for holding values between stages – Input vs. Output Buffering – Block RAM (BRAM) vs Registers • Focus on output buffering w/ registers – “Delay Pipe” houses a strip of P values Port 0 BRAM Port 1 Register Delay Pipe P Registers

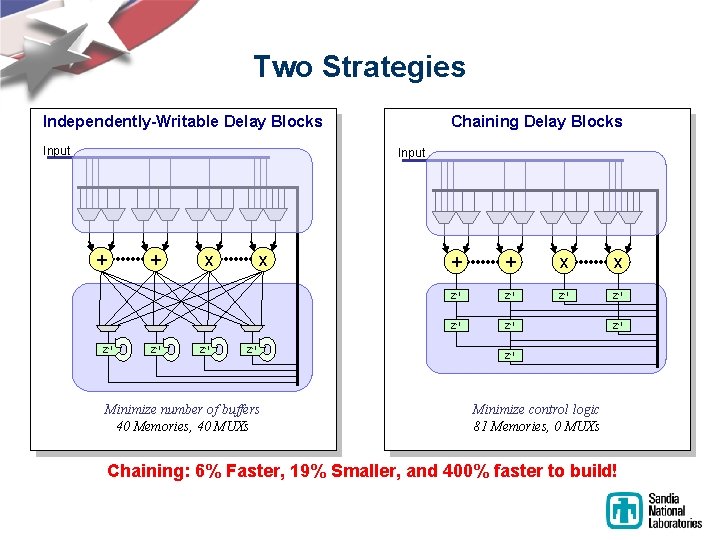
Two Strategies Independently-Writable Delay Blocks Input Chaining Delay Blocks Input + + Z-1 x Z-1 Minimize number of buffers 40 Memories, 40 MUXs + + x x Z-1 Z-1 Minimize control logic 81 Memories, 0 MUXs Chaining: 6% Faster, 19% Smaller, and 400% faster to build!

Outline • Overview – Reusing floating-point hardware • Adapting the Algorithm – Operation Scheduling – Mapping Operations to Units – Intermediate Data Values • Performance Observations – Ongoing Work: Automation • Summary

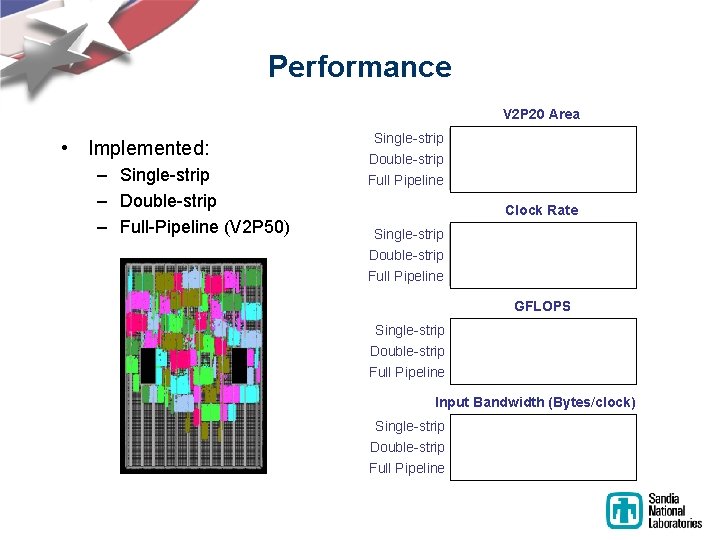
Performance V 2 P 20 Area • Implemented: – Single-strip – Double-strip – Full-Pipeline (V 2 P 50) Single-strip Double-strip 70% 79% 199% Full Pipeline Clock Rate Single-strip 155 MHz Double-strip Full Pipeline 148 MHz 142 MHz GFLOPS Single-strip Double-strip Full Pipeline 0. 9 1. 2 7. 1 Input Bandwidth (Bytes/clock) Single-strip Double-strip Full Pipeline 7. 6 11. 3 68

Ongoing Work: Automation • Natural fit for automation – Built our own tools – DFG analysis tools – VHDL generation • Experiment – – No strip mining Change # of FP units Change # Iterations Find # clocks for 128 iterations

Concluding Remarks • Reusing FP units enables FPGAs to process larger kernels – Apply traditional scheduling tricks to increase utilization – Algorithm shape affects performance – Simplicity wins • Simple DFG tools go a long ways – Easy to adjust parameters, generate hardware – Focus on kernels instead of complete systems