Floating Pointer Operation Floating number representation IEEE 754

Floating Pointer Operation § Floating number representation IEEE 754 standard § Floating point operations Addition, multiplications § FPU Organization § MIPS floating instructions § Accuracy of floating point operation Based on Chapter 4. 8 Floating Point, [Hennessy and Patterson] 9/19/2021 CMPUT 229 1

Floating Representation § Three components Sign • Identified the number • positive or negative Mantissa (fraction, significand) Exponent § Follows IEEE 754 standard 9/19/2021 CMPUT 229 2

$IEEE 754 Floating Number S exponent 1 N = -1 8 S 9/19/2021 fraction$

IEEE 754 Floating Number S exponent 1 N = -1 8 S 9/19/2021 fraction (precision) significand 23 x 1. Fraction x 2 CMPUT 229 exponent – 127 3

Floating point double precision A floating number of 64 bits S exponent 1 11 significand 20 32 N = -1 S 9/19/2021 x 1. significand x 2 CMPUT 229 exponent – 1023 4

Floating Point Operations § Float point addition 1 Consider 9. 888 X 10 + 1. 610 * 10 1 = = = -1 -1 9. 888 X 10 + 0. 016 * 10 -1 1 9. 888 X 10 + 0. 016 * 10 1 10. 015 * 10 1. 002 * 10 2 9/19/2021 CMPUT 229 5

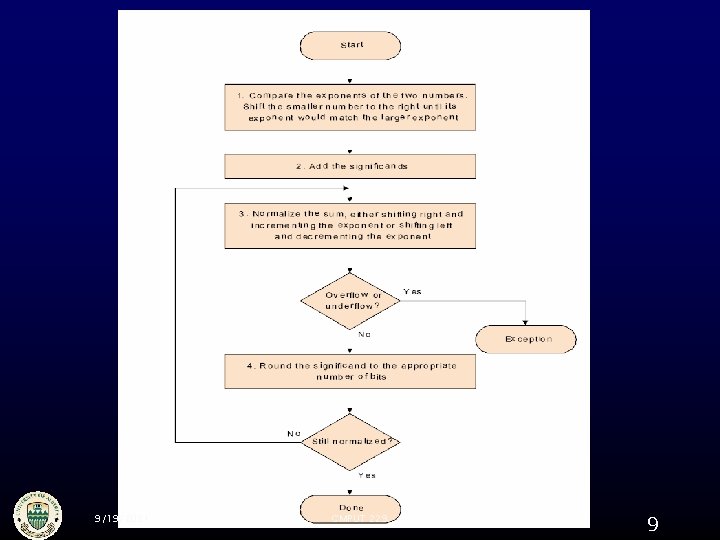
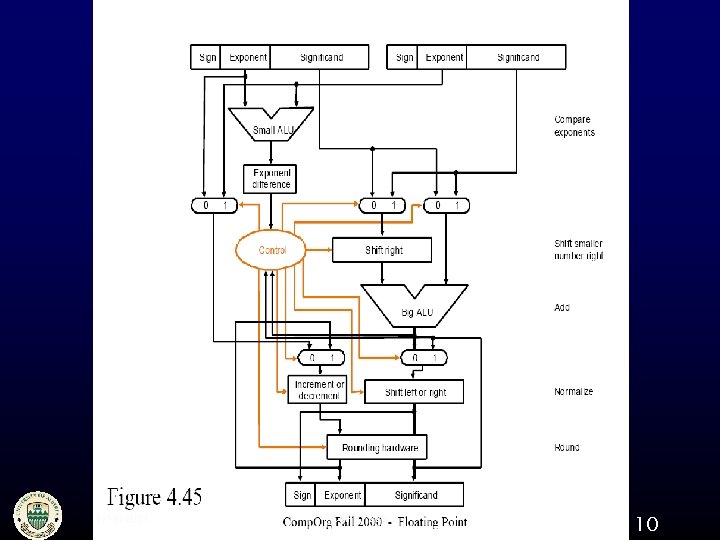
Floating point addition § Line up the binary points Shift one of the numbers § Add significands using integer addition § Normalize the result § Might need to round the result 9/19/2021 CMPUT 229 6

§ Rounding Intermediate results (in the middle of multiplication or addition operations) might not fit The internal representation of intermediate values uses 2 extra bits • Round and guard 9/19/2021 CMPUT 229 7

9/19/2021 CMPUT 229 8

9/19/2021 CMPUT 229 9

9/19/2021 CMPUT 229 10

Floating point multiplication 3 1. 3 x 10 times 3. 0 x 10 1 = 3. 9 * 10 9/19/2021 CMPUT 229 1 11

§ Floating Point Multiplication Add exponents Multiply significands Normalize result 9/19/2021 CMPUT 229 12

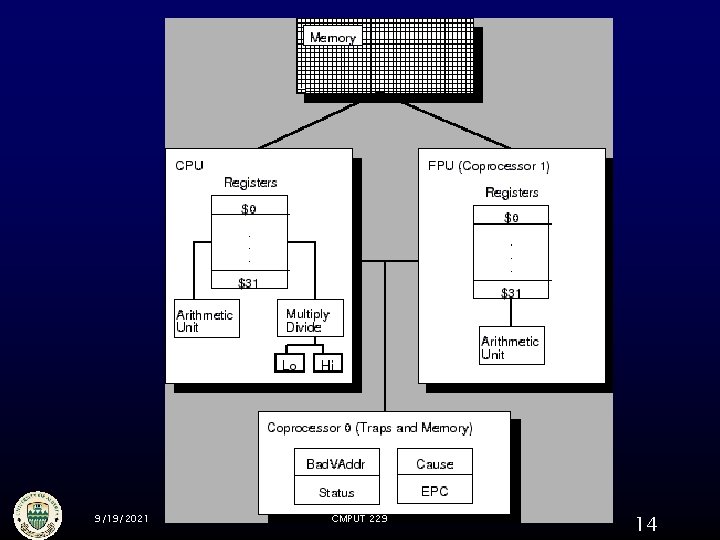
FPU Organization § 32 floating registers $f 0, $f 1, …, $f 31 May be used in pairs for double precision numbers 9/19/2021 CMPUT 229 13

9/19/2021 CMPUT 229 14

MIPS Floating Point Instructions § add. d FRdest, FRsrc 1, FRsrc 2 Floating Point Addition Double § add. s FRdest, FRsrc 1, FRsrc 2 Floating Point Addition Single Compute the sum of the floating float doubles (singles) in registers FRsrc 1 and FRsrc 2 and put it in register FRdest. 9/19/2021 CMPUT 229 15

§ mul. d FRdest, FRsrc 1, FRsrc 2 Floating Point Multiply Double § mul. s FRdest, FRsrc 1, FRsrc 2 Floating Point Multiply Single Compute the product of the floating float doubles (singles) in registers FRsrc 1 and FRsrc 2 and put it in register FRdest. 9/19/2021 CMPUT 229 16

§ div. d FRdest, FRsrc 1, FRsrc 2 Floating Point Divide Double § div. s FRdest, FRsrc 1, FRsrc 2 Floating Point Divide Single Compute the quotient of the floating float doubles (singles) in registers FRsrc 1 and FRsrc 2 and put it in register FRdest. 9/19/2021 CMPUT 229 17

§ sub. d FRdest, FRsrc 1, FRsrc 2 Floating Point Subtract Double § sub. s FRdest, FRsrc 1, FRsrc 2 Floating Point Subtract Single Compute the difference of the floating float doubles (singles) in registers FRsrc 1 and FRsrc 2 and put it in register FRdest. 9/19/2021 CMPUT 229 18

§ mov. d FRdest, FRsrc Move Floating Point Double § mov. s FRdest, FRsrc Move Floating Point Single Move the floating float double (single) from register FRsrc to register FRdest. 9/19/2021 CMPUT 229 19

§ Accuracy Double can represent many more integers exactly. In fact, everything int can represent, double can represent, exactly. Every result that integer arithmetic can compute correctly and exactly, double arithmetic can compute correctly and exactly. Largest power of ten: a 64 -bit double can represent all integers exactly, up to: 1, 000, 000 (actually 2^53. . . +2^53). 9/19/2021 CMPUT 229 20