Floating Point Representation Fixed Point Notation The decimal

Floating Point Representation

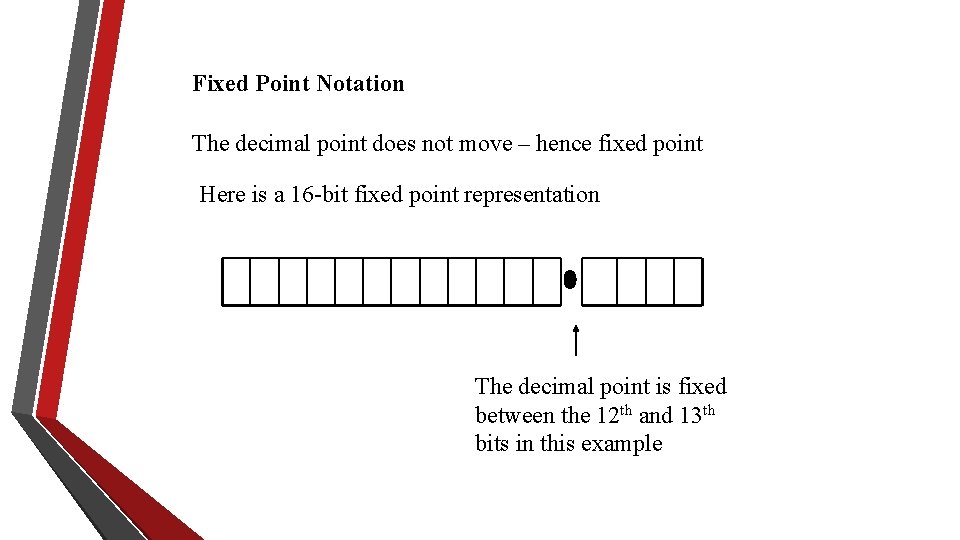
Fixed Point Notation The decimal point does not move – hence fixed point Here is a 16 -bit fixed point representation The decimal point is fixed between the 12 th and 13 th bits in this example

Fixed Point Notation For Example…. 0 0 0 0 1 1 The value of this number would be…. 1 1 0 0

Fixed Point Notation For Example…. 2 0 4 8 0 1 0 2 4 0 5 2 1 6 3 1 8 4 2 1 1 5 2 4 2 6 8 0 0 0 1 1 The value of this number would be…. ½ ¼ 1 1 / / 8 1 6 1 1 0 0

Fixed Point Notation For Example…. 2 0 4 8 0 1 0 2 4 0 5 2 1 6 3 1 8 4 2 1 1 5 2 4 2 6 8 0 0 0 1 1 ½ ¼ 1 1 / / 8 1 6 1 1 0 0 = 8+4+2+1+ ½ + ¼ = 15 ¾

Fixed Point Notation Advantage. Stores the number accurately Disadvantage. Can not represent a wide range of numbers. E. g 4000 0 r 0. 0001 This disadvantage can be solved by introducing a floating point All real numbers in computer systems are stored using floating point notation

Floating Point Notation In standard notation we represent numbers like this. . 2. 56 x 104 = 2 5 6 0 0. 0 The 4 here determines the position of the decimal point

Floating Point Notation In floating point notation it’s the same principle just in base 2. . 0. 1110010 x 24 = 0 1 1 1 0. 0 16 0 8 1 = 14. 25 4 1 2 1 1 0 ½ 0 ¼ 1 1/8 0

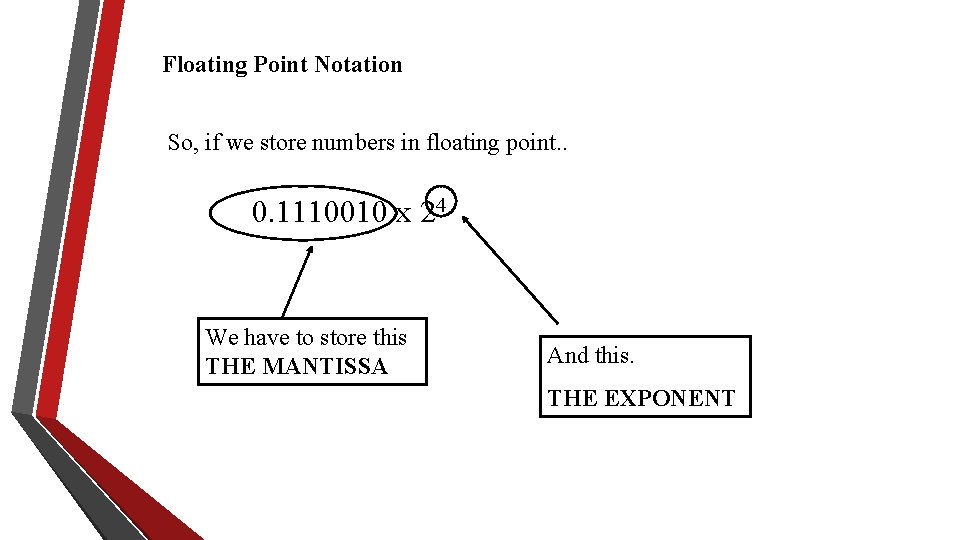
Floating Point Notation So, if we store numbers in floating point. . 0. 1110010 x 24 We have to store this THE MANTISSA And this. THE EXPONENT

Imagine a 12 bit number with 8 bit mantissa and 4 bit exponent 01 1 1 0 0 0 0 Mantissa – holds the precision 0 0 1 1 Exponent – holds the power of 2 the mantissa should be multiplied by

Imagine a 12 bit number with 8 bit mantissa and 4 bit exponent 4 2 1 01 1 1 0 0 0 0 The decimal point always starts Between the first two digits Multiplying by 23 will have the effect of floating the decimal point 3 places to the right so…. 0 0 1 1 Calculate the exponent. In this case 3 so. . x 23

Imagine a 12 bit number with 8 bit mantissa and 4 bit exponent 4 2 1 01 1 1 0 0 0 0 1 Multiplying by 23 will have the effect of floating the decimal point 3 places to the right so…. 0 0 1 1

Imagine a 12 bit number with 8 bit mantissa and 4 bit exponent 4 2 1 01 1 1 0 0 0 0 1 2 Multiplying by 23 will have the effect of floating the decimal point 3 places to the right so…. 0 0 1 1

Imagine a 12 bit number with 8 bit mantissa and 4 bit exponent 4 2 1 01 1 1 0 0 0 0 1 2 3 Multiplying by 23 will have the effect of floating the decimal point 3 places to the right so…. 0 0 1 1

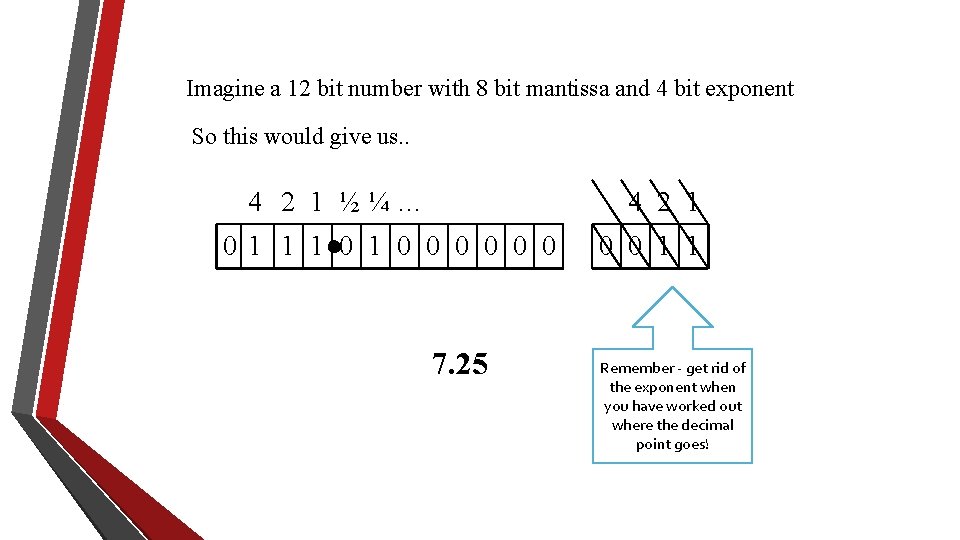
Imagine a 12 bit number with 8 bit mantissa and 4 bit exponent So this would give us. . 4 2 1 ½¼… 4 2 1 01 1 1 0 0 0 0 7. 25 0 0 1 1 Remember - get rid of the exponent when you have worked out where the decimal point goes!

Positive Mantissa and Negative exponent Both the mantissa and exponent are represented in twos complement. Imagine this 12 bit number with 8 bit mantissa and 4 bit exponent -8 4 2 1 0 0 0 0 The decimal point always starts Between the first two digits 2 -3 Multiplying by means floating the decimal point 3 places left so. . 1 1 0 1 Calculate the exponent. – 8 + 4 + 1 = -3 So 2 -3

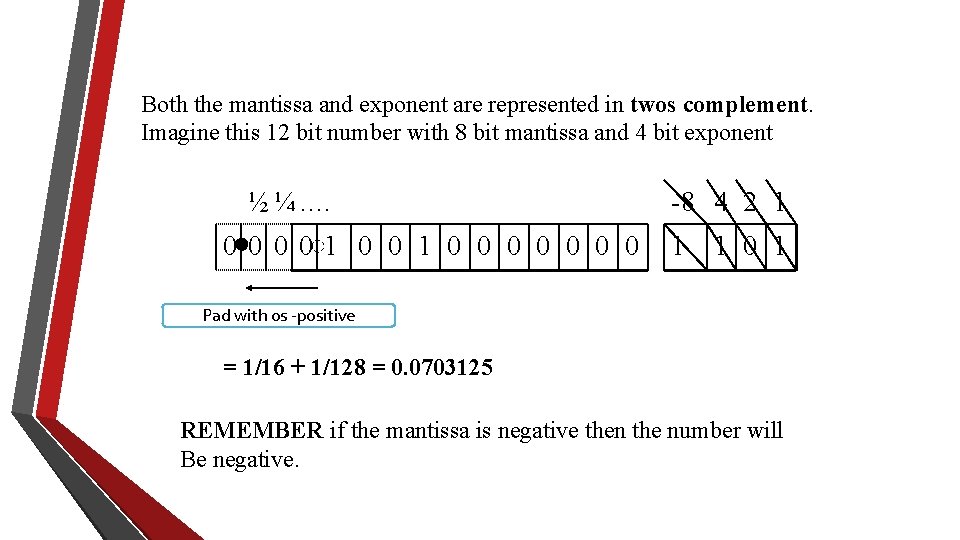
Both the mantissa and exponent are represented in twos complement. Imagine this 12 bit number with 8 bit mantissa and 4 bit exponent ½ ¼ …. 0 0 1 0 0 0 0 0 -8 4 2 1 1 1 0 1 Pad with 0 s -positive = 1/16 + 1/128 = 0. 0703125 REMEMBER if the mantissa is negative then the number will Be negative.

Negative mantissa and Positive exponent Both the mantissa and exponent are represented in twos complement. Imagine this 12 bit number with 8 bit mantissa and 4 bit exponent 1 0 1 1 1 0 0 0 0 8 4 2 1 0 0 1 1 3 -8 4 2 1 1/2 1 0 1 1 1 -8+2+1+0. 5= -4. 5

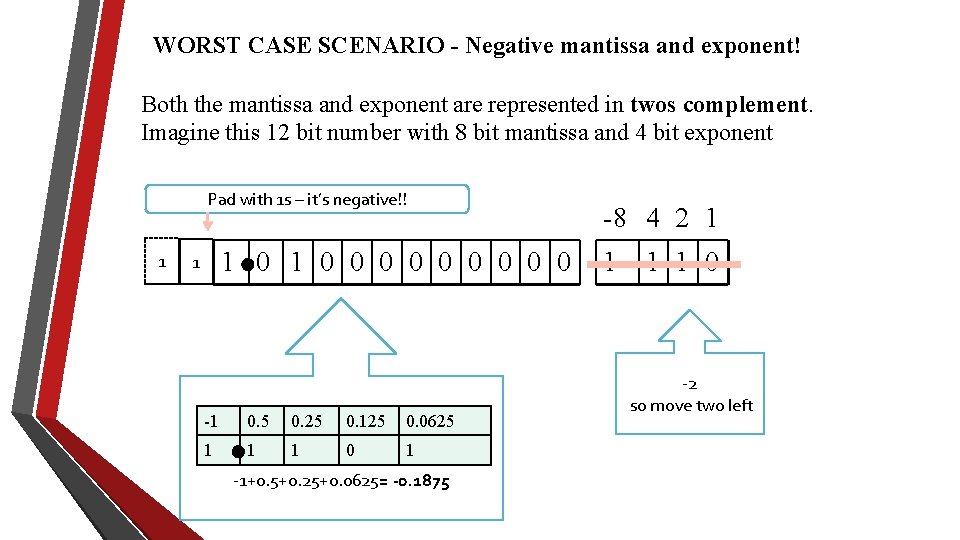
WORST CASE SCENARIO - Negative mantissa and exponent! Both the mantissa and exponent are represented in twos complement. Imagine this 12 bit number with 8 bit mantissa and 4 bit exponent Pad with 1 s – it’s negative!! 1 1 0 0 0 0 0 1 -1 0. 5 0. 25 0. 125 0. 0625 1 1 1 0 1 -1+0. 5+0. 25+0. 0625= -0. 1875 -8 4 2 1 1 0 -2 so move two left

Floating Point Notation Advantage. Being able to move the decimal point allows us to represent a much greater range of numbers Disadvantage. Some loss of precision because some bits have to be used to hold the exponent (where the decimal point should be)

Normalisation. Imagine these 12 bit numbers with 8 bit mantissa and 4 bit exponent 0011000000 0010 0110000000 0001 Work out their values. What do you notice? 0000110000 0100 Yes – its the same number 1. 5! We normalise floating point numbers to ensure the most efficient standard representation.

Floating Point Notation Normalisation. • This ensures a floating point number is held in the most efficient way possible in order to maximise precision. • It also ensures all floating point numbers are held in the same way.

Floating Point Notation Normalisation. Positive Mantissa must begin 01 Negative Mantissa must be begin 10

Floating Point Notation Normalisation. Positive Mantissa must begin 01 Negative Mantissa must begin 10 When we adjust the mantissa we must change the exponent.

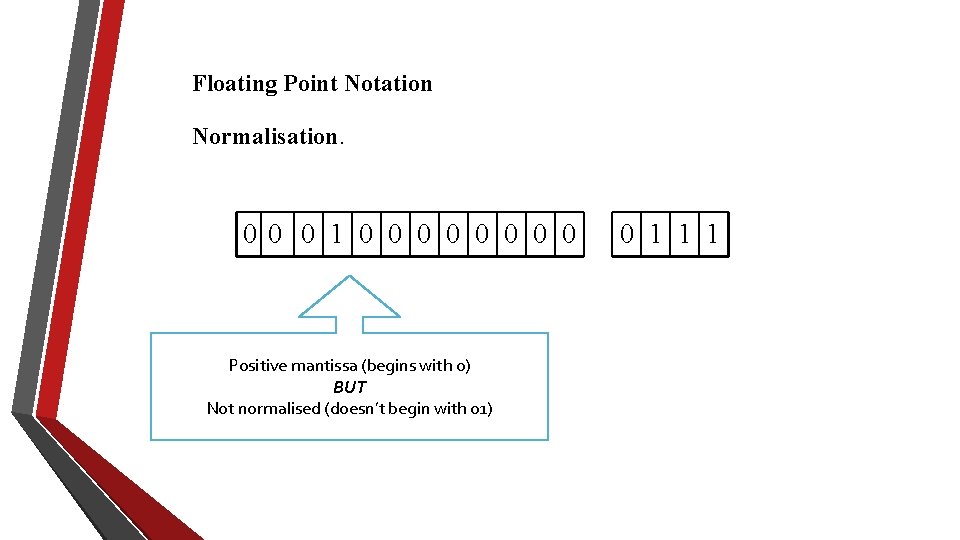
Floating Point Notation Normalisation. 00 0 1 0 0 0 0 Positive mantissa (begins with 0) BUT Not normalised (doesn’t begin with 01) 0 1 1 1

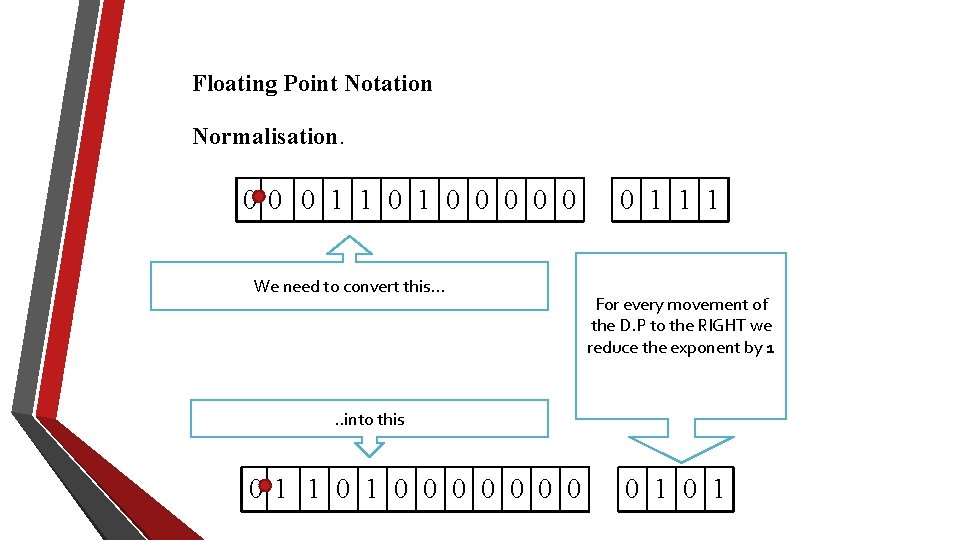
Floating Point Notation Normalisation. 00 0 1 1 0 0 0 We need to convert this. . . 0 1 1 1 For every movement of the D. P to the RIGHT we reduce the exponent by 1 . . into this 01 1 0 0 0 0 0 1

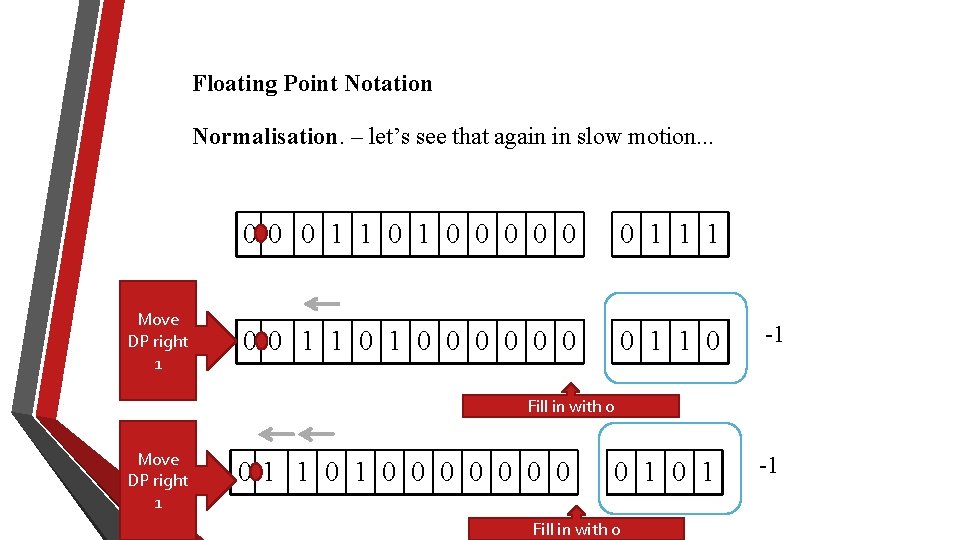
Floating Point Notation Normalisation. – let’s see that again in slow motion. . . Move DP right 1 00 0 1 1 0 0 0 0 1 1 1 00 1 1 0 0 0 0 1 1 0 -1 0 1 -1 Fill in with 0 Move DP right 1 01 1 0 0 0 0 Fill in with 0

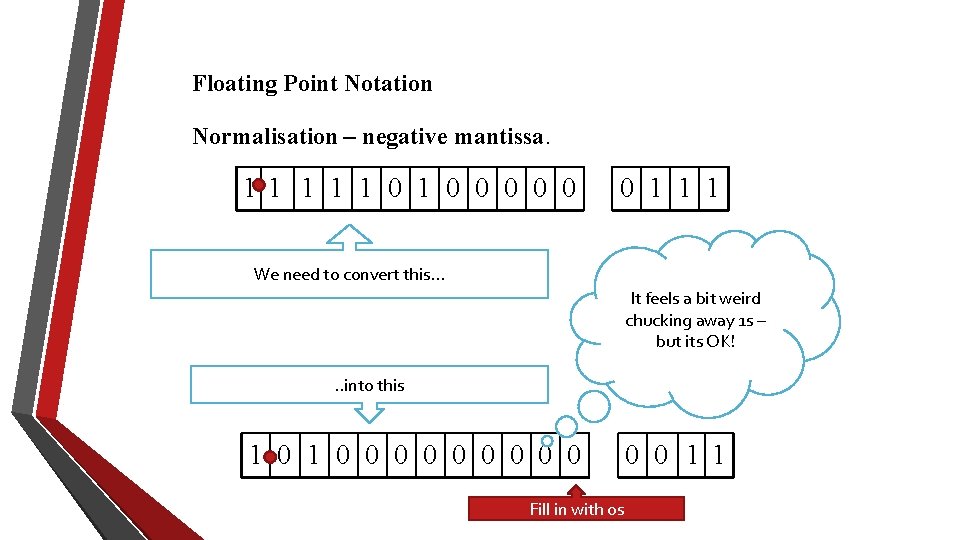
Floating Point Notation Normalisation – negative mantissa. 11 1 0 1 0 0 0 1 1 1 We need to convert this. . . It feels a bit weird chucking away 1 s – but its OK!. . into this 1 0 0 0 0 0 Fill in with 0 s 0 0 1 1

Converting Real numbers to floating point 1. Get the number 11. 25 2. Work out its fixed point binary representation Its POSITIVE so make sure there’s a 0 on the front! 01011. 01 3. Move the decimal point into the normalised position (between the first 0 and 1) 0. 101101 That needed 4 steps to the left so the exponent is +4 0100

Converting Real numbers to floating point 4. Check your answer!! 0. 1011010 0100 0. 1011010 x 24 01011. 010 =11. 25 CORRECT!

TRY THESE – They get harder!! (use 8 bit mantissa and 4 bit exponent) 5. 75 0. 125 (1/8 TH) 01011100 0011 01100000 01000000 1110 -8. 5 -0. 0625 (- 1/16 TH) 10111100 0100 10000000 1100

Floating Point – Things to remember 1. The decimal point always starts between the first two digits of the mantissa. 2. Positive mantissa = positive number 3. Negative mantissa = negative number 4. Positive exponent = number is going to be 1 or bigger (bigger than -1 if negative) 5. Negative exponent = number is going to be smaller than 0. 5. (-0. 5 if negative) 6. Pad negative mantissas with 1 s at the front 0 s at the back 7. Pad positive mantissas with 0 s at the front 0 s at the back 8. Normalised positive numbers’ mantissa must start 01 9. Normalised negative numbers’ mantissa must start 10.

Floating Point Errors Precision Errors – number gets chopped because it wont fit in available number of bits. Rounding Error – number gets rounded to fit into the available number of bits absolute – difference between the number you wanted and the number actually stored. relative – the percentage difference. Cancellation Errors – Adding a small number to a big number may cause us to lose the small number. Overflow – A number too big too be stored in the allocated space Underflow – A number too small to be stored in the allocated space

What type of error maybe generated? Storing an irrational number e. g. pi Precision/Rounding Multiplying two very large numbers Overflow Dividing a large number by a very small number Overflow Dividing a very small number by a very large number Underflow Adding a very small number to a very large number Cancellation

Assuming you wanted to store the number 3. 6 but the closest representation in floating point you could manage was 3. 5 What is the absolute rounding error? 0. 1 abs(3. 6 – 3. 5) What is the relative rounding error? 0. 28 absolute error number wanted 0. 1 3. 6