Flexures for Optics Outline n Brief overviews of

Flexures for Optics

Outline n Brief overviews of micro flexures n Focus on macro flexures in this tutorial n Beam bending n Symmetry -> precision n Degree of freedom (DOF) n Applications

Micro Flexures Comb drive Tip-tilt mirrors discrete vs analog

Optical MEMS devices Resonant frequency of the comb drive depends on the ions hitting the pads Analog tip-tilt mirror

Motivation n Need nanometer precision to manipulate light. n “Stage” and “driving mechanism”. n Sticktion is a problem encountered with screw-type driving mechanisms. n Use piezoelectric, capacitive, magnetic, photon, … to drive the “stage”.

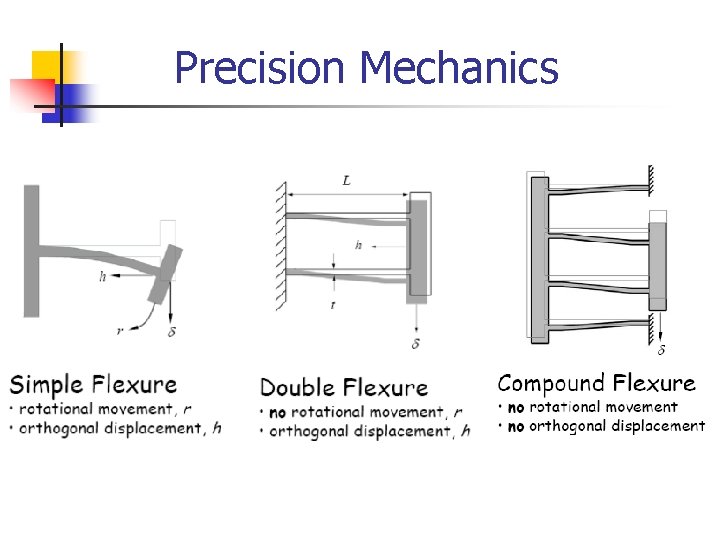
Precision Mechanics

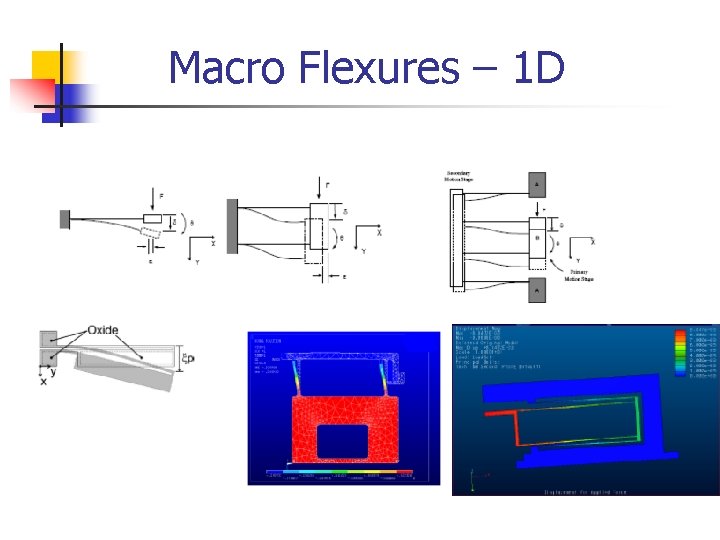
Macro Flexures – 1 D

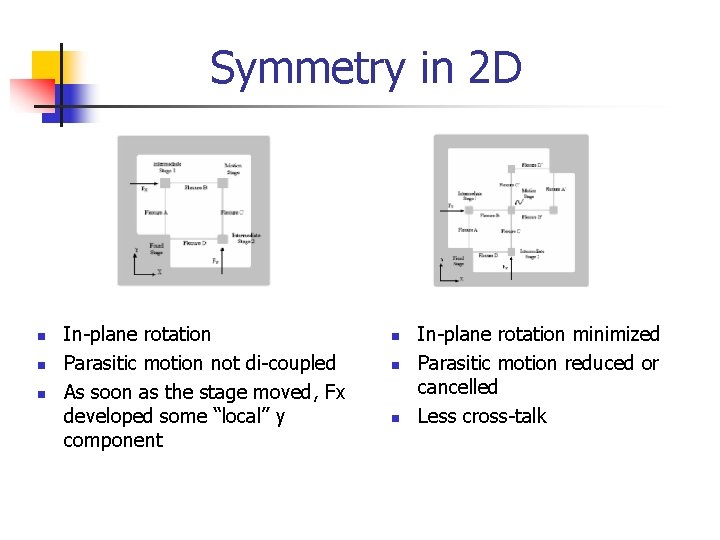
Symmetry in 2 D n n n In-plane rotation Parasitic motion not di-coupled As soon as the stage moved, Fx developed some “local” y component n n n In-plane rotation minimized Parasitic motion reduced or cancelled Less cross-talk

Parallelogram n n n In-plane rotation constrained Parasitic motion reduced As soon as the stage moved, Fx developed some “local” y component n n n In-plane rotation constrained Parasitic motion further reduced or cancelled Less cross-talk

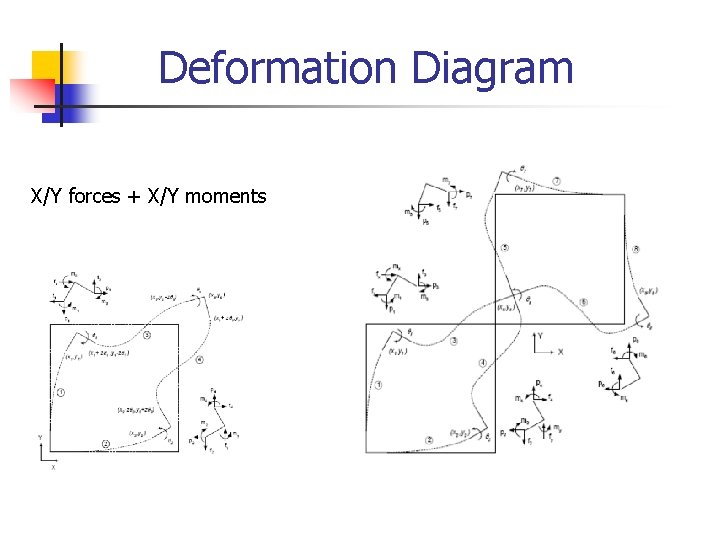
Deformation Diagram X/Y forces + X/Y moments

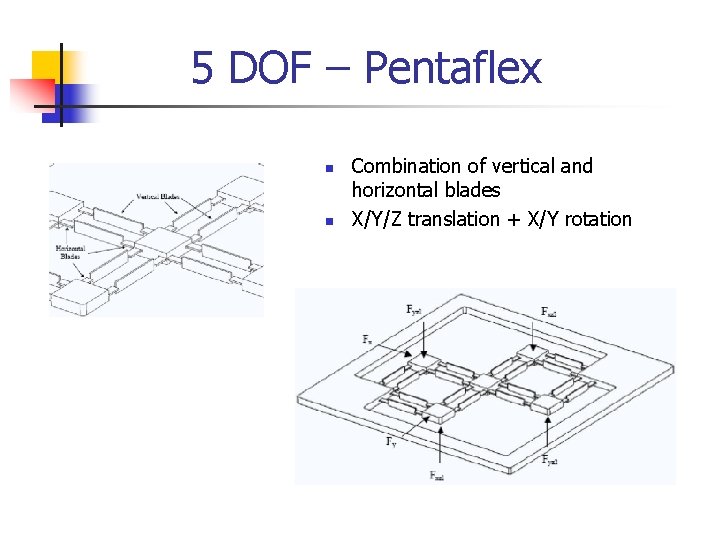
5 DOF – Pentaflex n n Combination of vertical and horizontal blades X/Y/Z translation + X/Y rotation

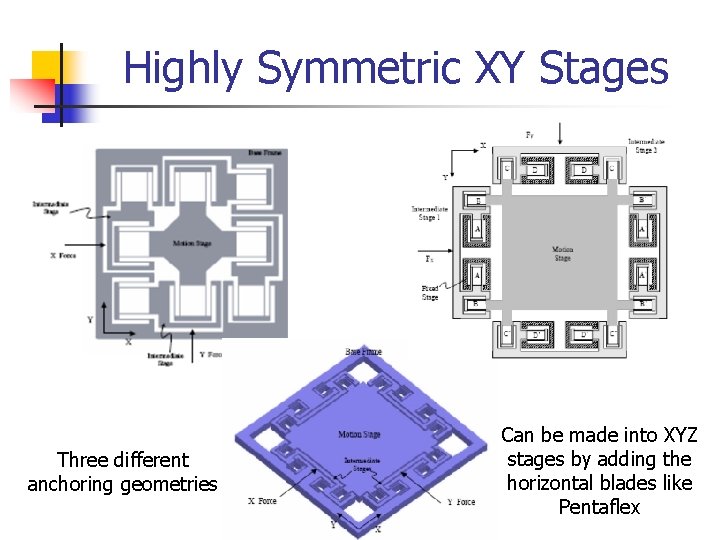
Highly Symmetric XY Stages Three different anchoring geometries Can be made into XYZ stages by adding the horizontal blades like Pentaflex

Diaphragm Flexures Provide out-of-plane (z, f, g) motions Constrain the other in-plane (x, y, q) motions (Voice-coil, pressure sensor, flow control, MEMS devices)

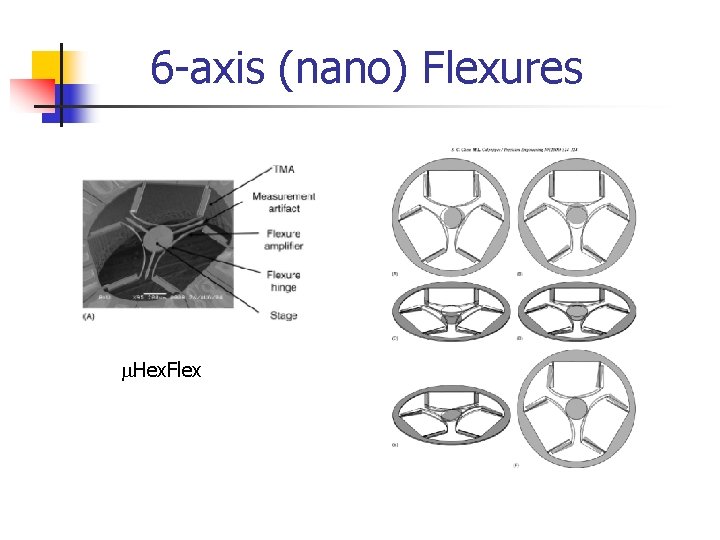
6 -axis (nano) Flexures m. Hex. Flex

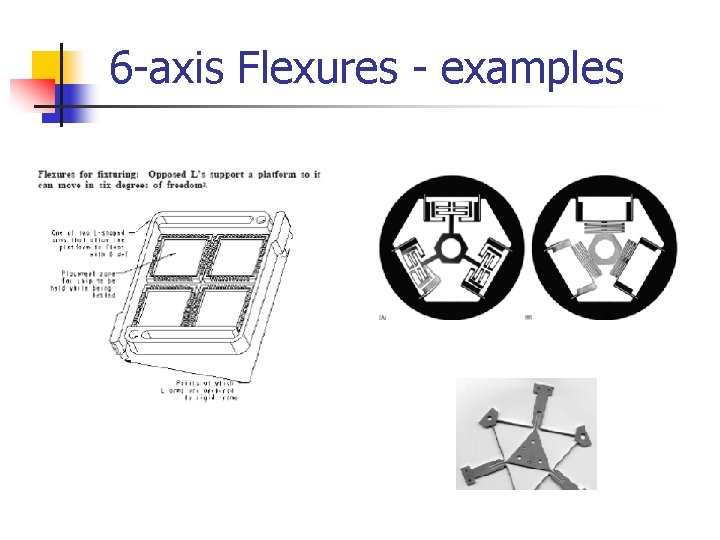
6 -axis Flexures - examples

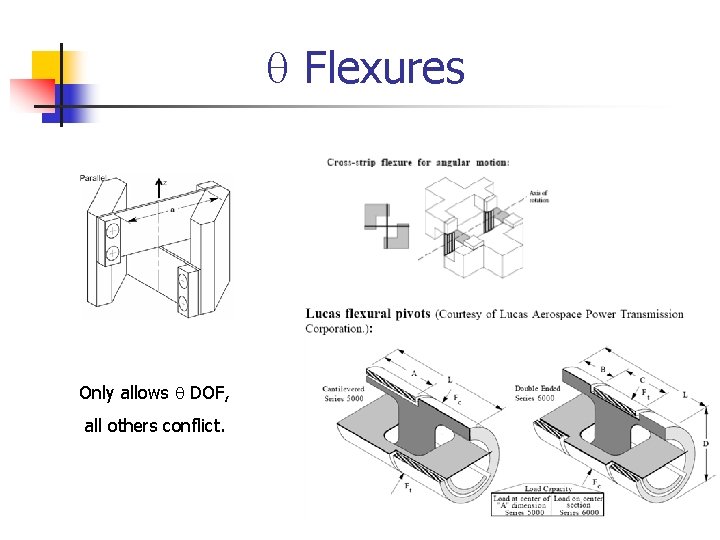
q Flexures Only allows q DOF, all others conflict.

Tip-tilt Flexures Remove axial misalignment between two parts (shear), but does not remove torque/moment.

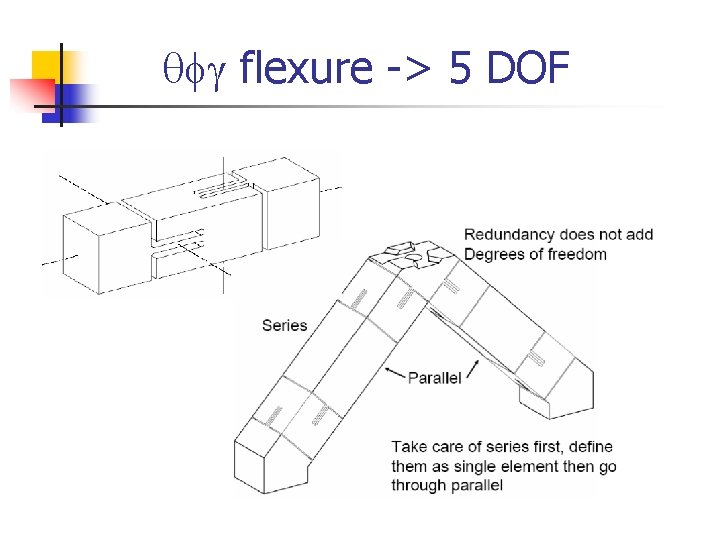
qfg flexure -> 5 DOF

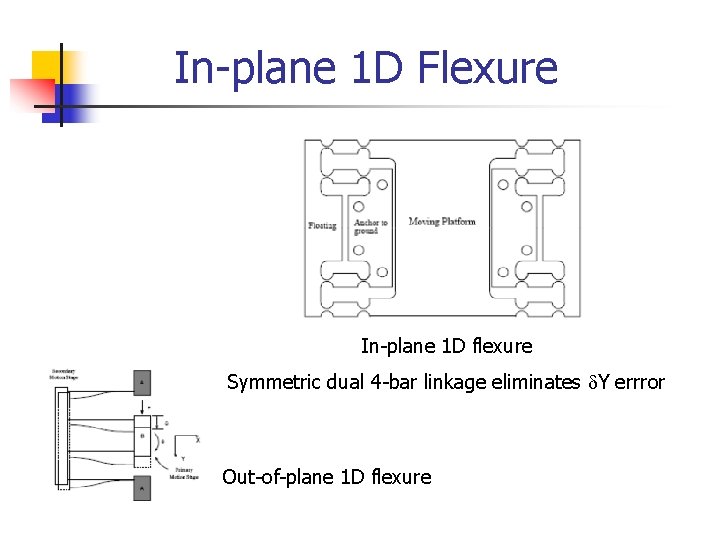
In-plane 1 D Flexure In-plane 1 D flexure Symmetric dual 4 -bar linkage eliminates d. Y errror Out-of-plane 1 D flexure

Uniform Shaft Loading

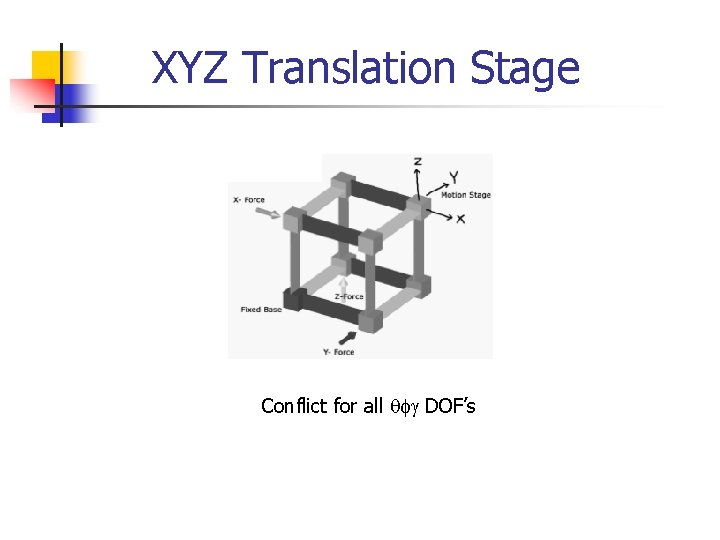
XYZ Translation Stage Conflict for all qfg DOF’s

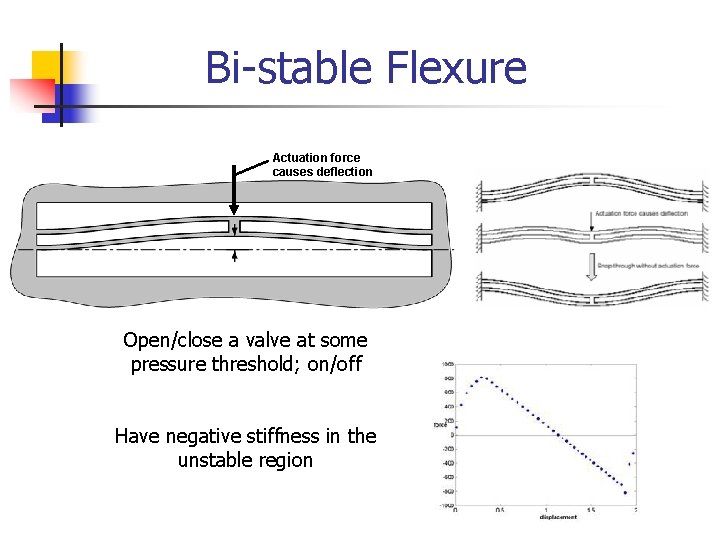
Bi-stable Flexure Actuation force causes deflection Open/close a valve at some pressure threshold; on/off Have negative stiffness in the unstable region

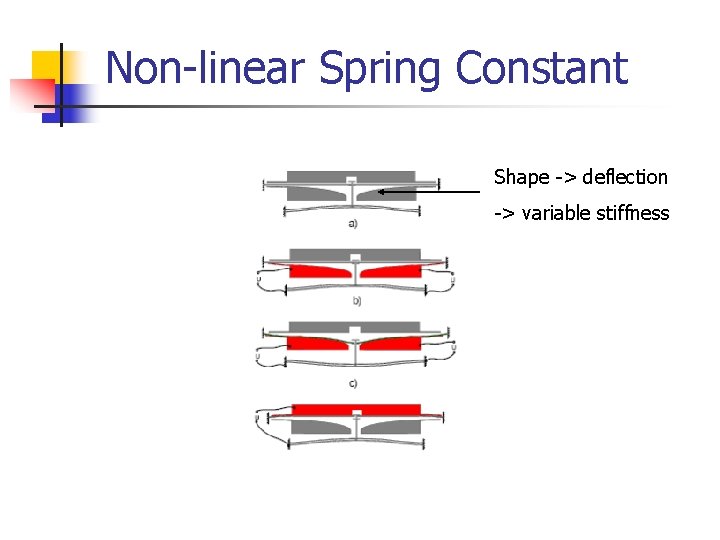
Non-linear Spring Constant Shape -> deflection -> variable stiffness

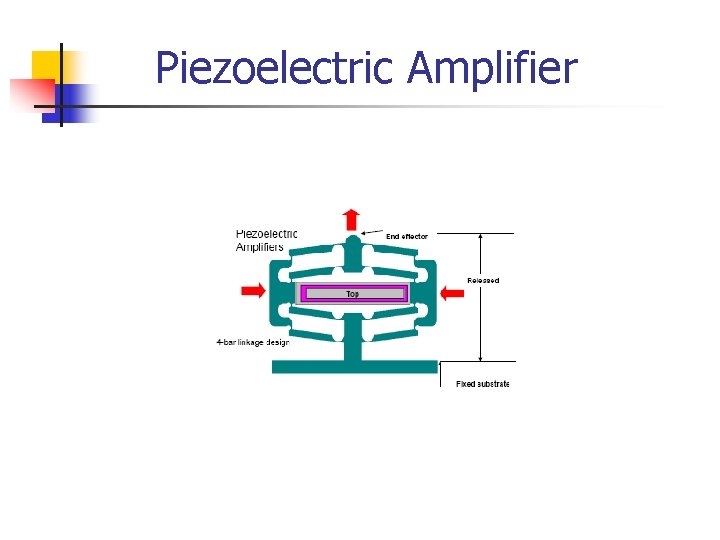
Piezoelectric Amplifier

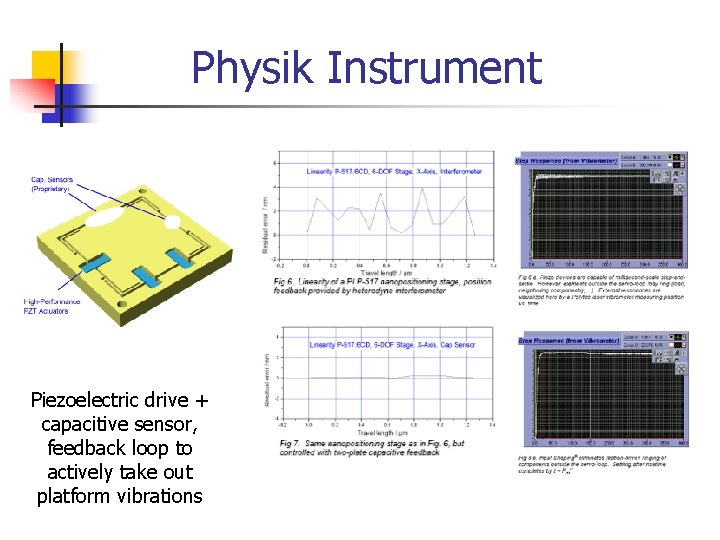
Physik Instrument Piezoelectric drive + capacitive sensor, feedback loop to actively take out platform vibrations

Conclusion n n n Use flexure to avoid sticksion. Use symmetry to cancel/de-couple motions. In-plane vs out-of-plane configurations Flexures for translation, rotation, and any combination of DOF (1 -6 DOF). Dynamic range and linearity. Soft flexure -> low resonant frequency, stiff flexure -> high actuation force. References: see Flexure. For. Optics. doc