Flashback 10 8 12 In the figure below

Flashback 10 -8 -12 • In the figure below, points A and B are on opposite banks of a small stream. Point C is on the same bank of the stream as point Band approximately 18 meters from B. The measure of CBA is 45°, and the measure of BCA is 60°. • Which of the following expressions gives the approximate distance, in meters, between point A and point B ? (Note: For PQR, where p, q, and r are the lengths of the sides opposite P, Q, and R, respectively, . ) A. B. C. D. E.

Joke of the day What do you call more than one L?

A Parallel

Average rate of change • A rock breaks loose from the top of a tall cliff. What is its average speed during the first 2 seconds of fall? • Y= 16 t 2 • Average rate of change is Δy/ Δx (ex. 1 and 2)

Instantaneous rate of change • Find the speed of the rock at the instant t=2 • Δy/ Δx = 16(2 + h)2 - 16(2)2 h • Simplify • (Ex. 3 and 4)

• Graph [sin(x)]/x. • What is the limit at x=0? • Not all functions can be simplified like the previous examples, so we must define a limit and use properties of limits to find it.

The Definition of Limit at a Point Karl Weierstrass (1815 – 1897)

Properties of Limits • Sum: limit of the sum of 2 functions is the sum of their limits • Difference: limit of the difference of 2 functions is the difference of their limits • Product: limit of the product of 2 functions is the product of their limits • Constant multiple: limit of a constant times a function is the constant times the limit of the function. • Quotient: limit of the quotient of 2 functions is the quotient of their limits provided the limit of the denominator is not zero. • Power: limit of a rational power of a function is the power of the limit of the function provided the limit of the function is a real number.

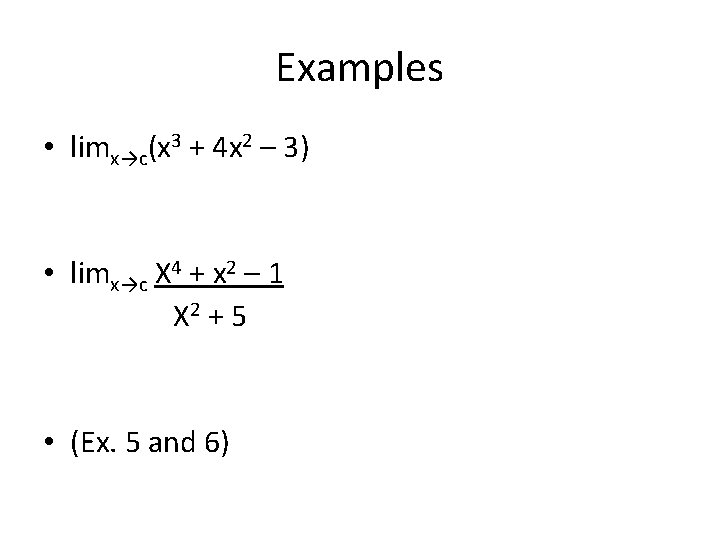
Examples • limx→c(x 3 + 4 x 2 – 3) • limx→c X 4 + x 2 – 1 X 2 + 5 • (Ex. 5 and 6)

Assignment • P. 66 Exercises 1 -6

Exit Slip 1. What do you know about limits?