Fizyka statystyczna Statistical Physics Ryszard Wojciechowski Wydzia Fizyki














![Równanie Liouville’a gdzie [ ] oznacza nawias Poissona. Ostatecznie otrzymujemy: 15 Równanie Liouville’a gdzie [ ] oznacza nawias Poissona. Ostatecznie otrzymujemy: 15](https://slidetodoc.com/presentation_image_h/fa6832bc4976189558ef37213dae7cfd/image-15.jpg)



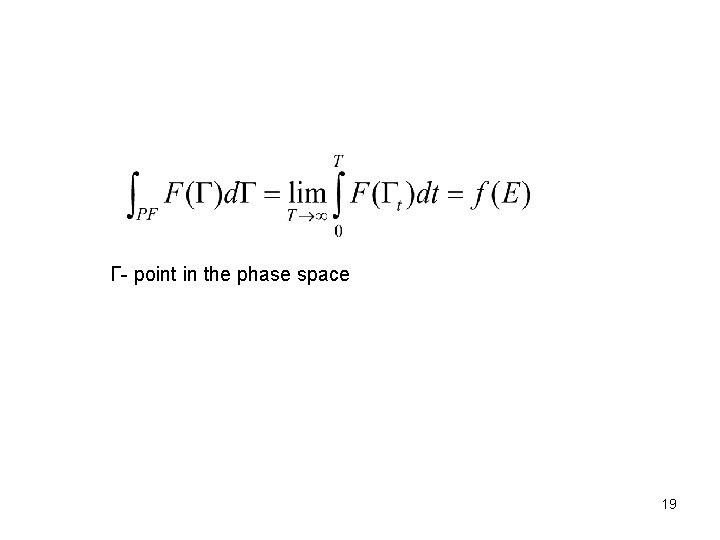



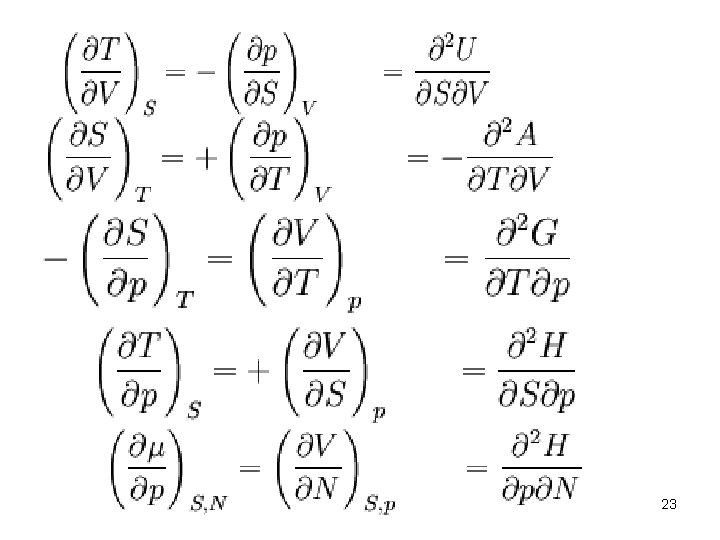


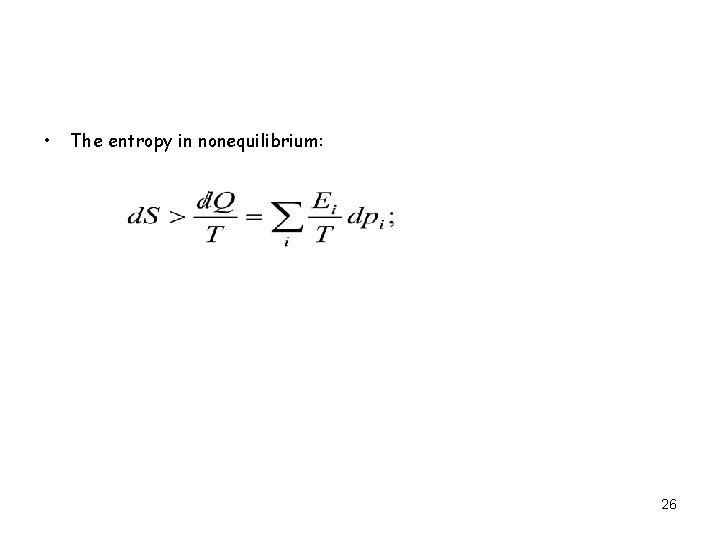










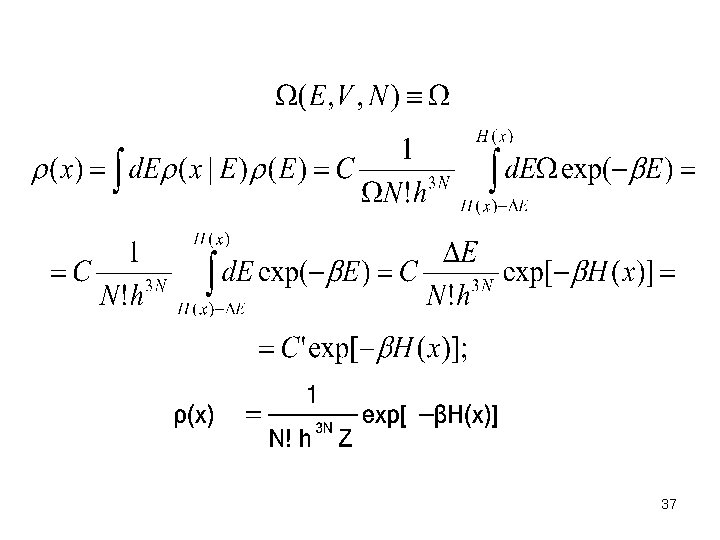


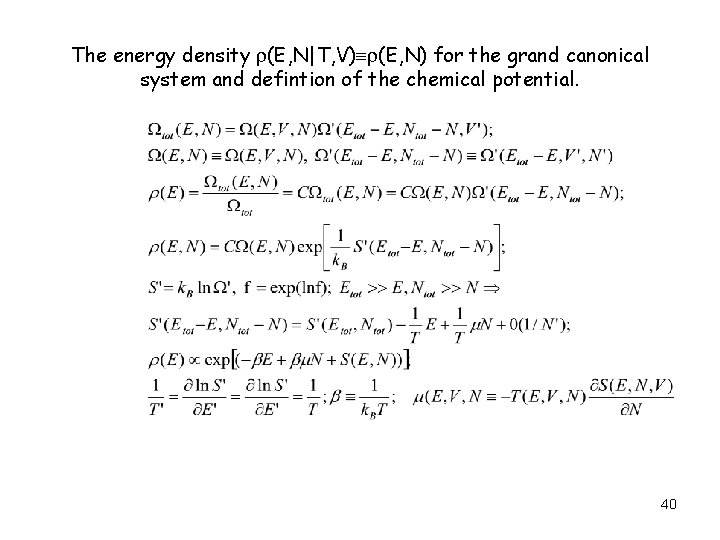





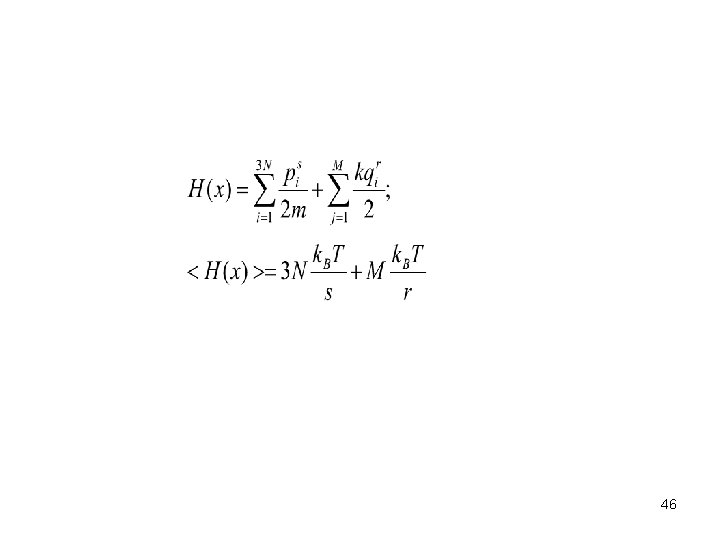



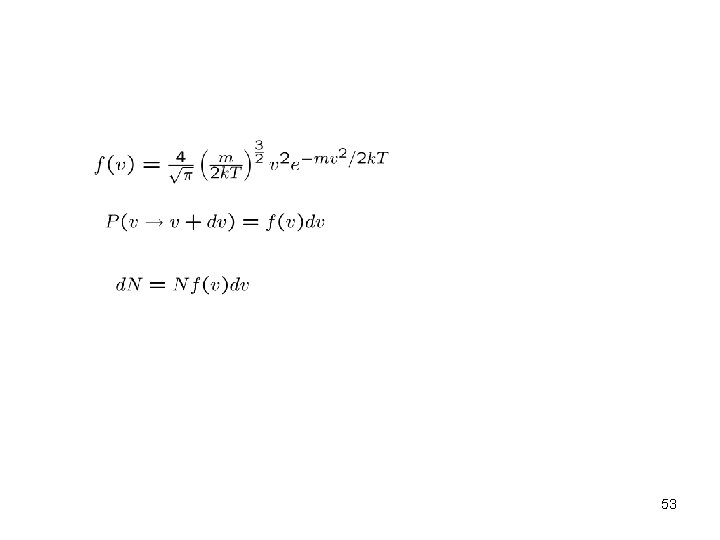











![Przykładowe temperatury degeneracji kwantowej Układ Gęstość[cm 3] T 0[K] gazowy H 2 ciekły 4 Przykładowe temperatury degeneracji kwantowej Układ Gęstość[cm 3] T 0[K] gazowy H 2 ciekły 4](https://slidetodoc.com/presentation_image_h/fa6832bc4976189558ef37213dae7cfd/image-69.jpg)







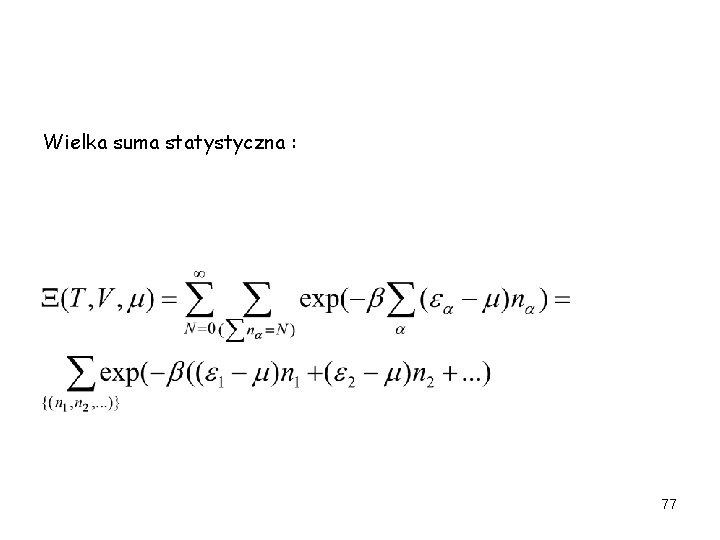

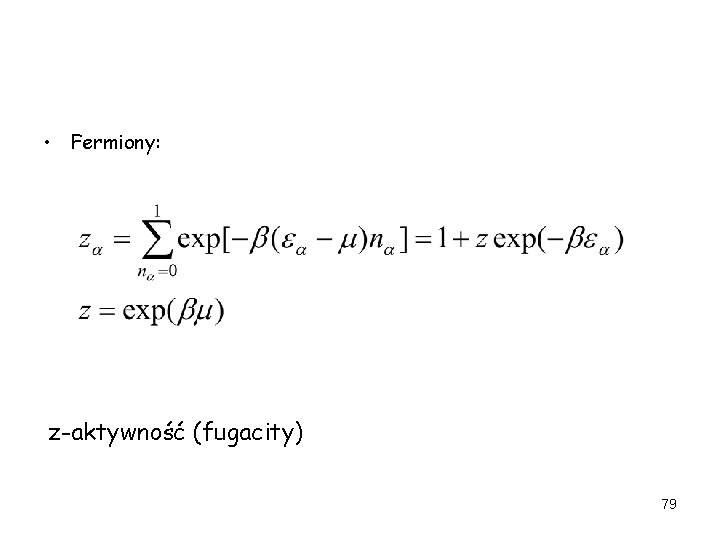






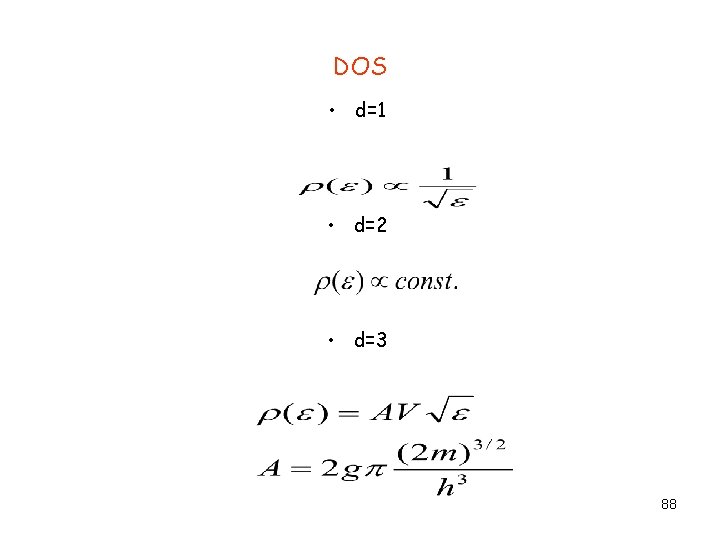




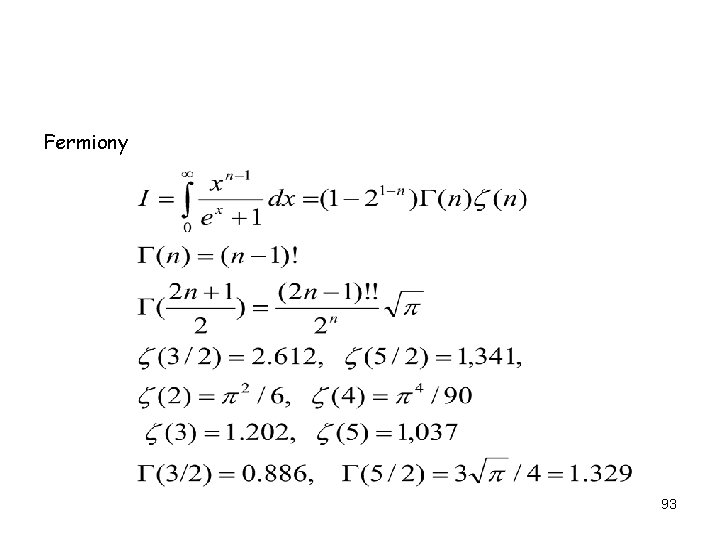





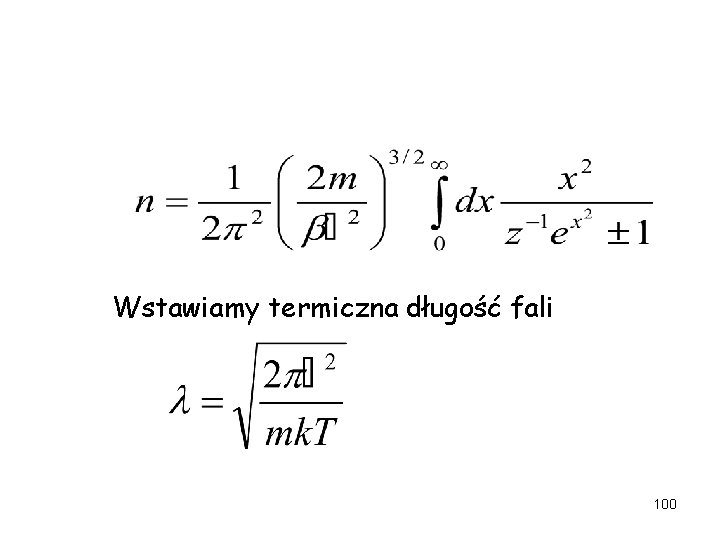
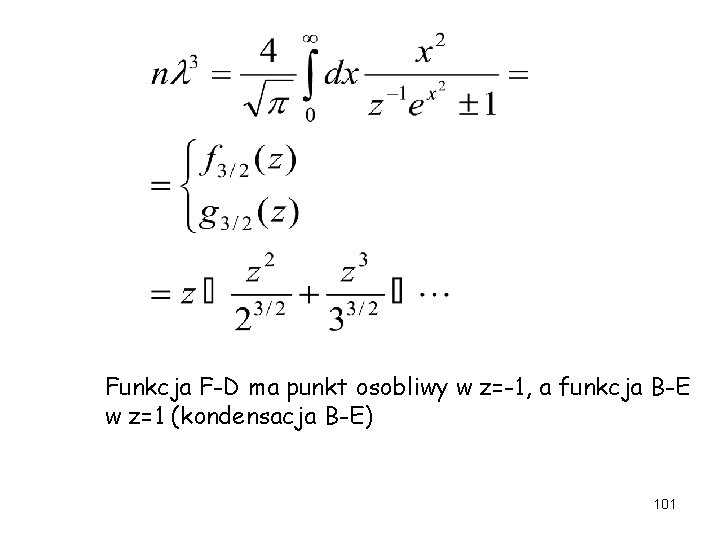

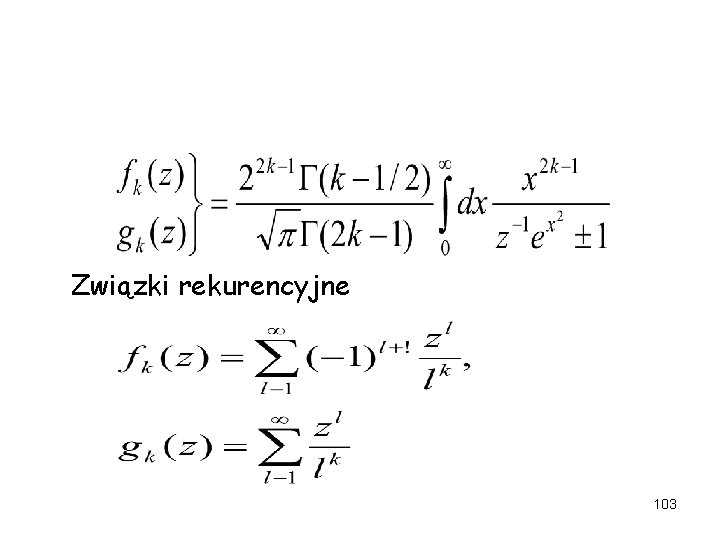
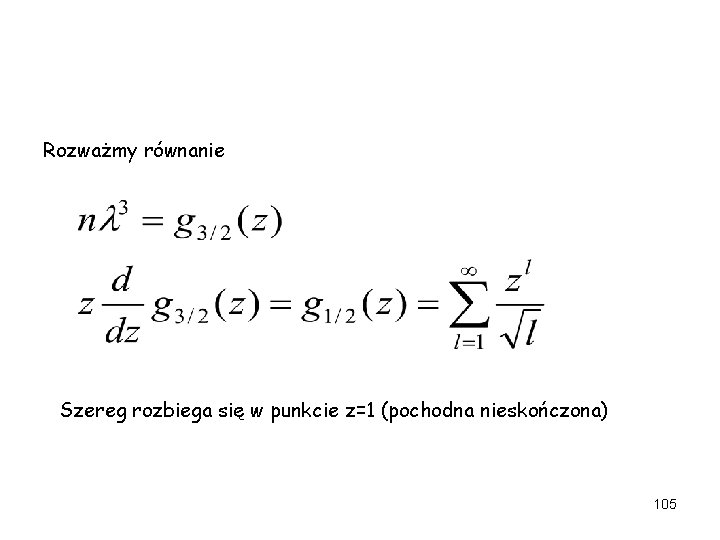



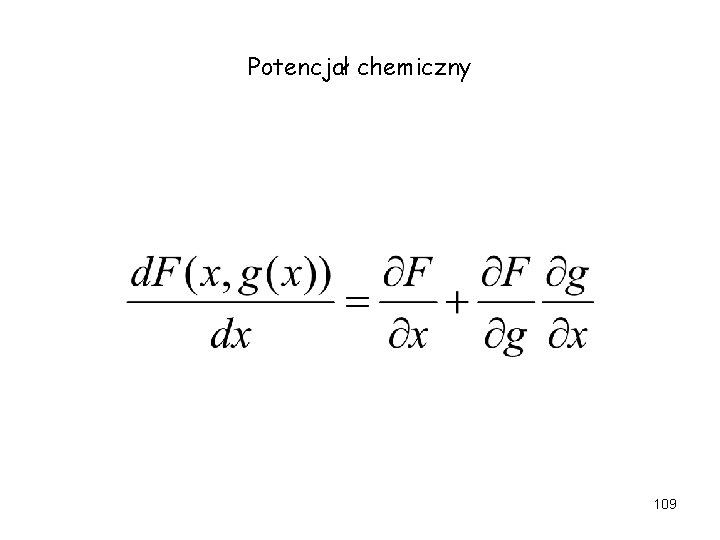












- Slides: 124

Fizyka statystyczna Statistical Physics Ryszard Wojciechowski Wydział Fizyki, UAM (2008/2009) 1

Równanie Liouville’a Twierdzenie o zachowaniu objętości fazowej (tw. Liouville’a) Stan klasyczny: punkt w 6 N wymiarowej przestrzeni fazowej. Dla układu zachowawczego: równania ruchu to równania Lagrange’a: qi- współrzędna uogólniona N punktów materialnych (cząstek) 2

L=K-U- funkcja Lagrange’a; Kenergia kinetyczna; U- energia potencjalna układu. R. ruchu w formie hamiltonowskiej: H- funkcja Hamiltona (Hamiltonian) (q 1, q 2, …, q 3 N, p 1, p 2, …, p 3 N)=(X)- zbiór zmiennych kanonicznych 3

Opis statystyczny układu mechanicznego • Stan ‘mechaniczny’ jest całkowicie zdeterminowany przez (x)mikrostan; • Stan makroskopowy określony jest przez mierzalne makroskopowo parametry (wielkości fizyczne) będące funkcjami zmiennych kanonicznych: Fk nie wyznacza wszystkich (X)→ opis statystyczny 4

• Fazowa gęstość (rozkład) prawdopodobieństwa ρ(X. t). Odpowiada ona warunkom w jakich znajduje się układ oraz uwzględnia symetrię układu. (założenie o równych prawdopodobieństwach a priori) • Prawdopodobieństwo dla objętości G: Warunek unormowania: Średnia wartość wielkości fizycznej F(X): 5

• Odchylenie standardowe: 6

• Zespół fazowy: zbiór punktów fazowych, odpowiadający wszystkim możliwym stanom (mikrostanom) danego układu; • Statystyczny zespół fazowy: zbiór stanów z przypisanym im prawdopodobieństwem (fazowa gęstość prawdopodobieństwa) → każdy punkt zespołu fazowego staje się zmienną losową. • Ruch zespołu fazowego można traktować jako ruch cieczy fazowej. • Dla układów hamiltonowskich (spełnione są r. Hamiltona) ciecz fazowa jest nieściśliwa. 7

Równanie ciagłości Dla cieczy nieściśliwej ρ=0 8

Dla cieczy w przestrzeni 6 N wymiarowej Wynika to z równań Hamiltona 9

• Twierdzenie Liouville’a o zachowaniu objętości fazowej mówi, że zachowana jest objętość dowolnej części 6 N wymiarowej przestrzeni fazowej, ograniczonej zamkniętą hiperpowierzchnią określoną przez punkty w przestrzeni fazowej, przedstawiające stany układu 10

Równanie ruchu zespołu fazowego Szukamy równania ruchu (ewolucji) dla fazowej gęstości prawdopodobieństwa w ρ(X, t) tzn. chcemy znaleźć ρ(X, t) z ρ(X, t=t 0). Niech G 0 będzie objętością fazową w chwili t 0. W chwili t G 0 przejdzie (zgodnie z r. Hamiltona) w objętość Gt i G 0= Gt. Z twierdzenia Liouville’a otrzymujemy: ρ(X(t), t)= ρ(X(t 0) , t 0), Gdzie X(t) i X(t 0) są współrzędnymi w przestrzeni fazowej związane równaniami Hamiltona. Wynika to z wzajemnej jednoznacznej odpowiedniości wszystkich punktów zawartych w objętości G 0 z wszystkimi punktami zawartymi w objętości Gt prawdopodobieństwo znajdowanie się układu w obszarze o objętości G 0 w chwili t 0 jest równe prawdopodobieństwu jego znajdowania w obszarze o objętości Gt w chwili t, pod warunkiem, że nie ingerowano w układ (np. poprzez dokonanie pomiaru) aby spowodować zmiany prawdopodobieństw. 11

Gęstość prawdopodobieństwa znajdowania się układu w obszarze o objętości Gt nie zmienia się w czasie: Z uogólnionego tw. Ostrogradzkiego: 12

Ostatni wzór wynika z uogólnienia następującego wzoru na przypadek 6 N wymiarowy: 13

Całka równa się zero dla dowolnego obszaru całkowania Gt: Korzystając z równań Hamiltona i warunku na nieściśliwość cieczy fazowej otrzymujemy 14
![Równanie Liouvillea gdzie oznacza nawias Poissona Ostatecznie otrzymujemy 15 Równanie Liouville’a gdzie [ ] oznacza nawias Poissona. Ostatecznie otrzymujemy: 15](https://slidetodoc.com/presentation_image_h/fa6832bc4976189558ef37213dae7cfd/image-15.jpg)
Równanie Liouville’a gdzie [ ] oznacza nawias Poissona. Ostatecznie otrzymujemy: 15

W przypadku kwantowym jest równanie von Neumanna, w którym zamiast nawiasu Poissona występuje komutator [ , ]/iћ W równowadze termodynamicznej 16

Z mechaniki wiemy, że dla N>3 ruch jest zazwyczaj chaotyczny, tzn. że dwa punkty bliskie sobie w chwili początkowej rozbiegają się wykładniczo w czasie. Jeżeli po ‘długim czasie trajektoria w przestrzeni fazowej pokryje całą podprzestrzeń o danej energii to mówimy, że układ jest ergodyczny. Nie ma pewności, że tak się stanie. 17

Układy ergodyczne (Ergodic systems) Można pokazać, że istnieją układy mechaniczne, których zachowanie zdeterminowane jest przez jedna całkę ruchu, a mianowicie energię (np. Birkhoff i Kołmogorow ). Są to tzw. Układy ergodyczne. Bardziej formalnie: układy metrycznie nierozkładalne tzn. takie, dla których przestrzeni fazowej nie można podzielić na dwa obszary tak, aby punkt fazowy pozostawał cały czas w jednym obszarze i nie mógł przejść do drugiego obszaru. Dla układów ergodycznych dostępne są wszystkie punkty podprzestrzeni fazowej odpowiadającej danej energii. (punkt fazowy może przebiegać dowolnie blisko podprzestrzeni danej energii). Można pokazać, że dla układów ergodycznych średnia czasowa wielkości mechanicznej (fizycznej) F(X) dla nieskończonego długiego czasu jest funkcja jedynie energii i nie zależy od innych całek ruchu. Oczywiście istnieją układy nieergodyczne np. . szkła, szkła spinowe) Hipoteza ergodyczna Zakładamy, że układ jest ergodyczny tzn. , że jego średnia czasowa jest równa średniej fazowej po zespole mikrokanonicznym (Boltzmann): 18
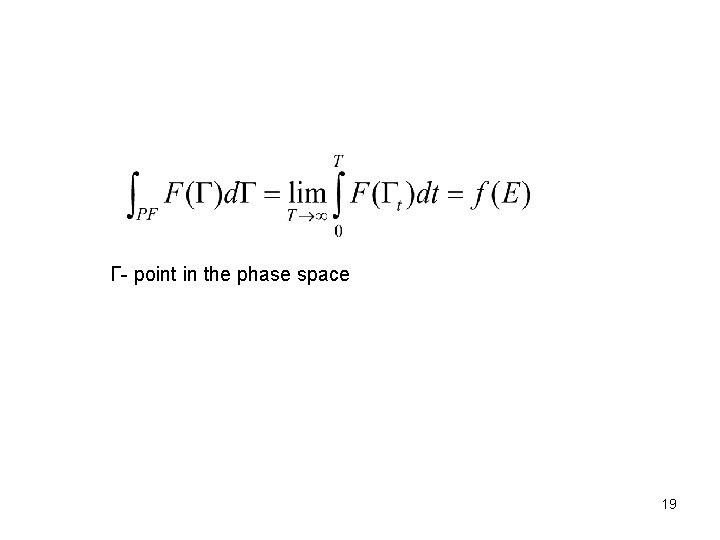
Γ- point in the phase space 19

Potencjały termodynamiczne i transformacja Legendre’a Thermodynamical potentials and the Legendre transform • • • Huan, p. 36, honer. P. 45 Potencjały Relacje Maxwella Różniczki zupełne i niezupełne Warunki stabilności 20

Maxwell relations The relations folow from the analitical properties of th thermodynamic potentials as functions of their natural variables (including the number of) particles) that is the symmetry of the second derivatives. 21

Can be obtained from: 22
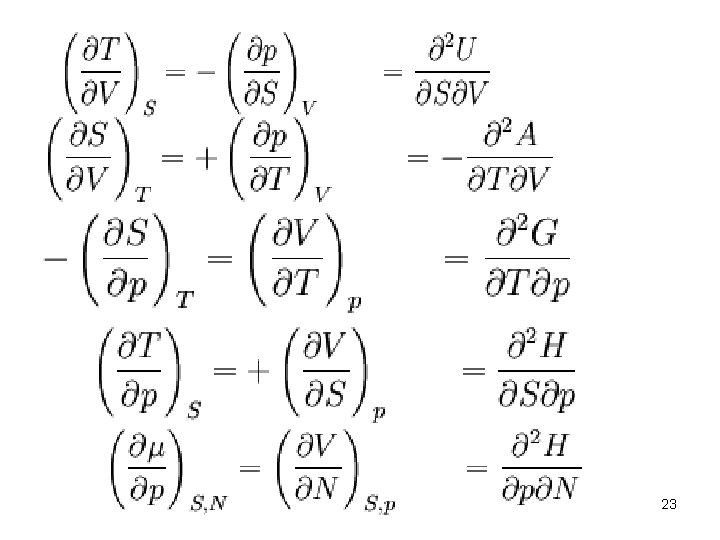
23

Zespoły kanoniczne Gibbsa i odpowiadajace im rozkłady prawdopodobieństwa • Zespół mikrokanoniczny (microcanonical ensemble): izolowany, stała objętość V i liczba cząstek N; Gęstość prawdopodobieństwa: ρ(p, q|E, V. N)= ρ(p, q) • Zespół kanoniczny (canonical ensemble): kontakt cieplny (średnia energia), stała objętość V i liczba cząstek N; Gęstość prawdopodobieństwa: ρ(p, q|V. N)=ρ(p, q) • Zespół wielki kanoniczny (grand canonical ensemble): wymiana energii i cząstek (układy otwarte) z otoczeniem, stała objętość; Gęstość prawdopodobieństwa: ρ(p, q|V)=ρ(p, q) 24

Changes of external conditions • The internal energy (heat and work are energy contributions which the system exchanges with its environment: • The entropy in equilibrium: 25
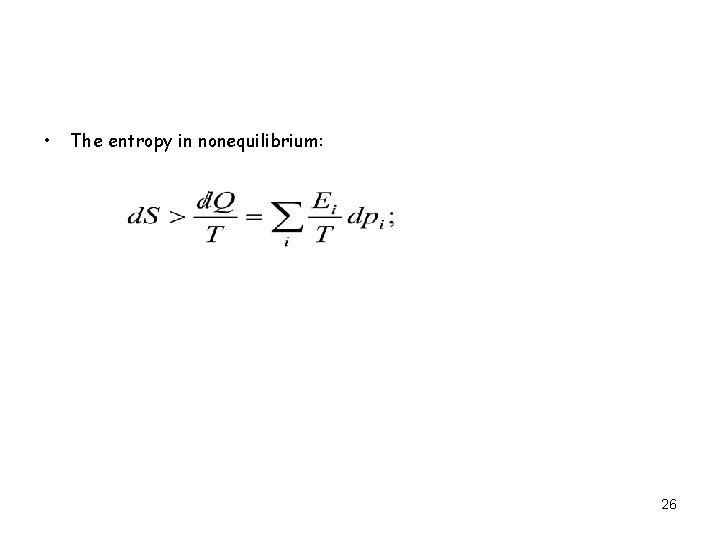
• The entropy in nonequilibrium: 26

The microcanonical systems • • H(x)=E. More realistic: E≤H(x)≤E+ΔE. The probability density: • The probability of finding the system in the microstate i: N!h 3 N-the natural volume in phase space for a microstate. • The entropy: 27

• Normalization: 28

• The microcanonical ensemble average of the observable A: 29

• The density of ststaes N(E, V, N) ( N(E)) is equal to the number of cells i. e. the number of microstates in the interval (E, E+ΔE): • Example: The integral over the momenta is equal to the volume of sphere in 3 N Dimensional space with radious (2 m. E)1/2 and is giwne by: 30

31

• The entropy with the indistinguishability of particle (N!) : For fixed volume and energy per particle the entropy is proportional to the number of particle N, as should be. Without the indistinguishability of particle (Nln. N would be missing) the entropy per particle would increase with N (for N infinite S is infinite!) in contradiction with the laws of classical thermodynamics. This is so called the Gibbs paradox. 32

The canonical system (ensemble): the system in thermal contact. • Two systems: (1): H(p, q) and H’(p’, q’) (thermostat, thermal, bath) in thermal contact i. e. we allow an exchange of energy (V, N, V’N’constants), while the total system: Etot =H’(p’, q’)+H(p, q) remains closed (we have to wait until the total system is in a stationary equlibrium state. How to get the probability density (E) for the energy of the system (1)? . The number of microstates of the total system in which the first system has the energy E: 33

• The number of microsttses (E) is a rapidly increasing function of the energy. Thus, (E) ’(Etot-E) has a very sharp maximum for macroscopic systems (N-very large). ln( (E) ’(Etot-E)) exhibits a maximum for the same value of the energy. 34

The energy density (E|T, V. N) (E) for the canonical system and defintion of the temperature. 35

The Boltzmann density (canonical density) (x|T, V, N) (x). • The conditional probability: P(A|B)-the probability of A when B is given; • The joint probability: P(A B)-the prob. For the occurrence of A and B; • P(A B)=P(A|B)P(B)=P(B|A)P(A); • Independence of random variables A and B: P(A B)=P(A)P(B); • A disjoint, complete partition of : the union- i. Bi= , Bi B= ; 36
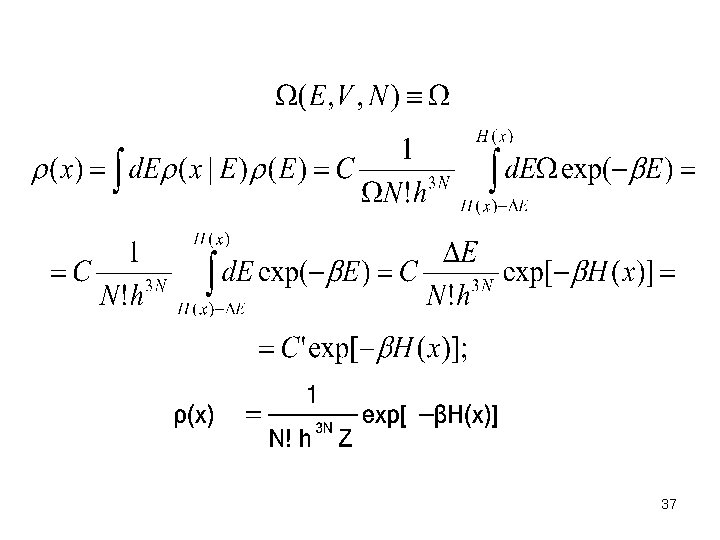
37

The partition function (the statistical sum) Z. The normalization condition, the free enrgy. 38

The grand canonical system (ensemble): the system in thermal contact. • Two systems: (1): H(p, q) and H’(p’, q’) (thermostat, thermal, bath) in thermal contact and with exchange of particles (V, , V’-constants), while the total system: Etot =H’(p’, q’)+H(p, q) remains closed (we have to wait until the total system is in a stationary equlibrium state. How to get the probability density (E, N) for the energy E and the number of particles N of the system (1)? . The number of microstates of the total system in which the first system has the energy E and the number of particles N: 39
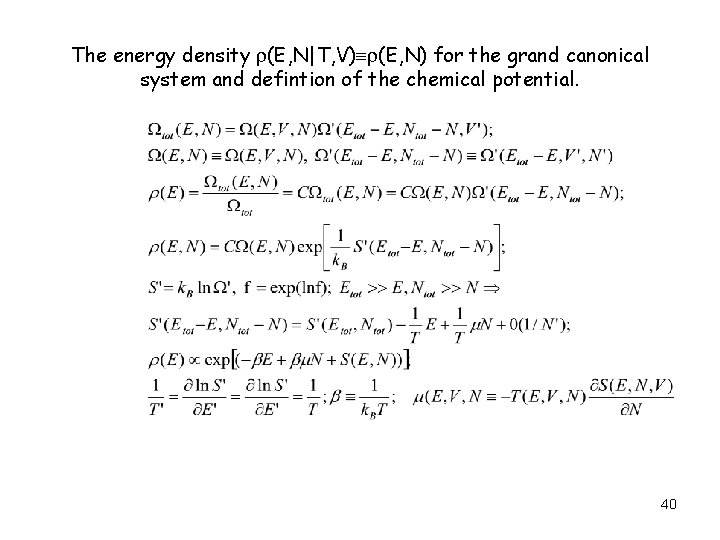
The energy density (E, N|T, V) (E, N) for the grand canonical system and defintion of the chemical potential. 40

• • The chemical potential is an intensive variable. For two systems in thermal contact and with an exchange of the particvles (V-const. ), the chemical potentials become equal in stationary equlibrium. Until the equlibrium state is reached, there is a flow of particles from the system with higher chemical potential to the system with lower chemical potential. Two systems with slightly different temperature and chemical potential: a quantity of energy d. E and a quantity of particles d. N flow into one system. Thus the change of the entropy for this system equals: 41

• The density for a microstate x=(p, q) of an N-particle system where N can vary from 0 to infinite: the grand or macrocanonical density. The grand canonical partition function Y and grand canonical potential: 42

Klasyczne gazy idealnerozkład Maxwella-Boltzmanna • • Fluktuacje w rozkładach kanonicznych Związek z entropią (maksymalizacja) Czynnik Boltzmanna Twierdzenie o ekwipartycji energii Rozkład szybkości Maxwella Ciepło właściwe (pojemność cieplna) Paradoks Gibbsa 43

The equipartition theorem A system of N classical particles: x (p 1, …p 3 N, q 1, …q 3 N). If the internal energy H(x) 0, x→ , then for arbitry polynomial function f(x): 44

The equipartition theorem: examples. The number of degrees of fredom f=3 N. 45
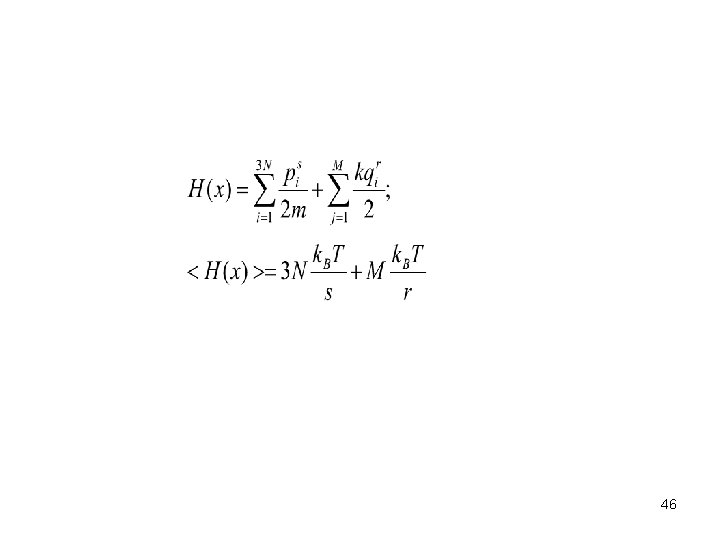
46

• Pojemności cieplne (heat capacities) • Funkcje reakcji (response functions) 47

1) Magnetic susceptibility: (R. M. Wilcox, Phys. Rev 174(2), 624(1968): Isothermal, adiabatic, , and isolated static susceptibility tensors; 2) Isothermal and adiabatic compressibilities: Isobaric Expansivity and Isochoric Tension: 48

49

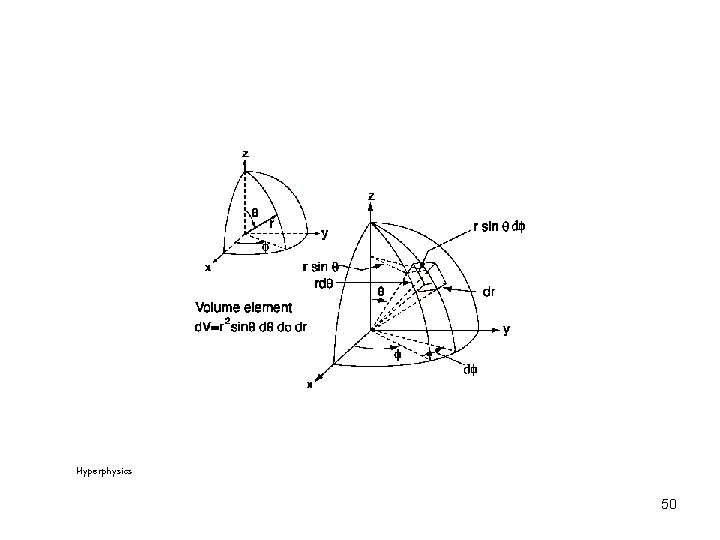
Hyperphysics 50

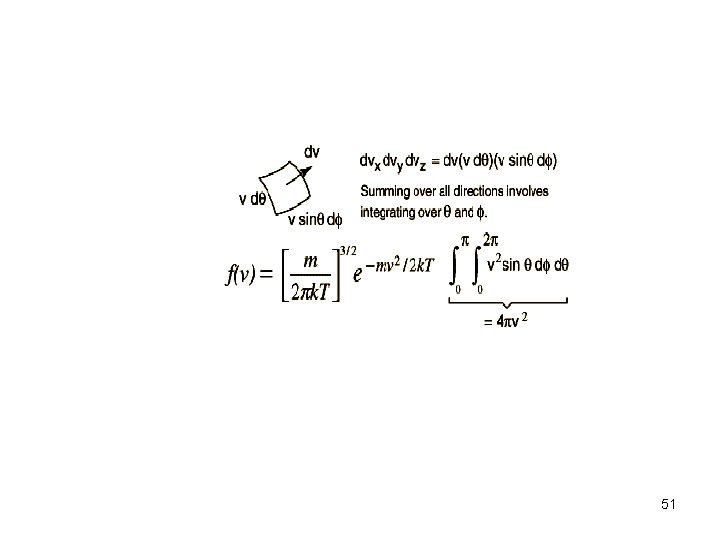
51

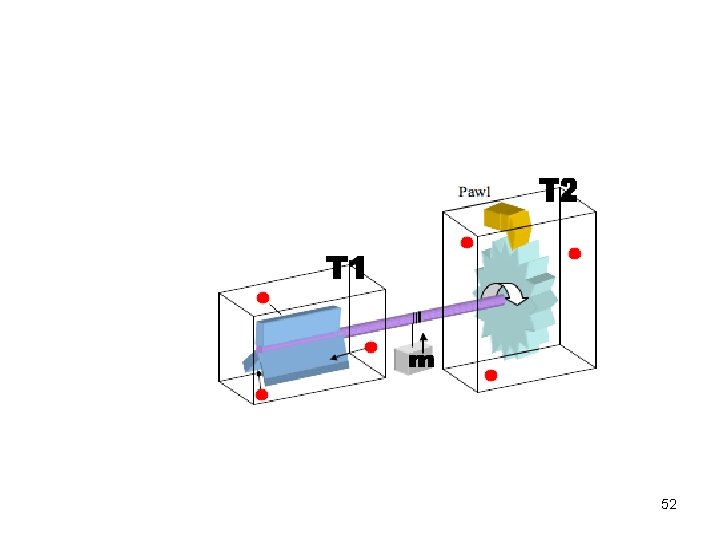
52
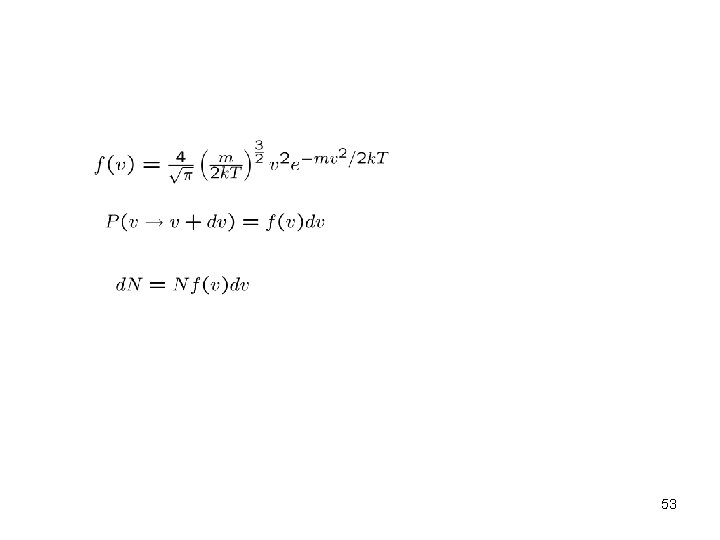
53

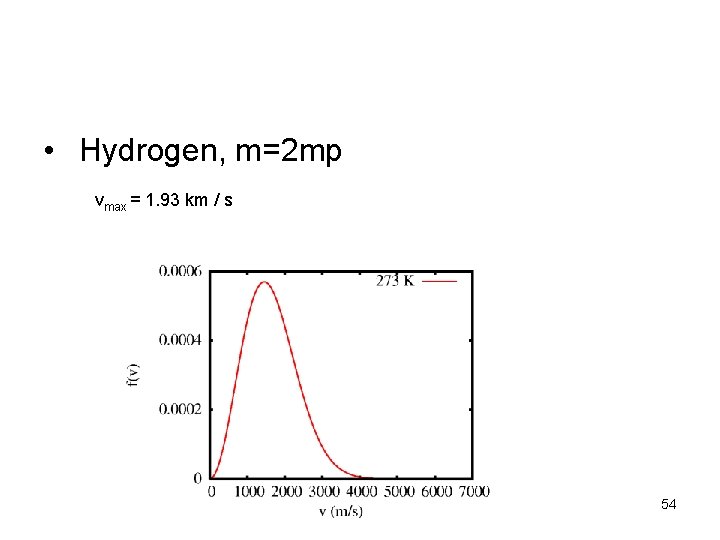
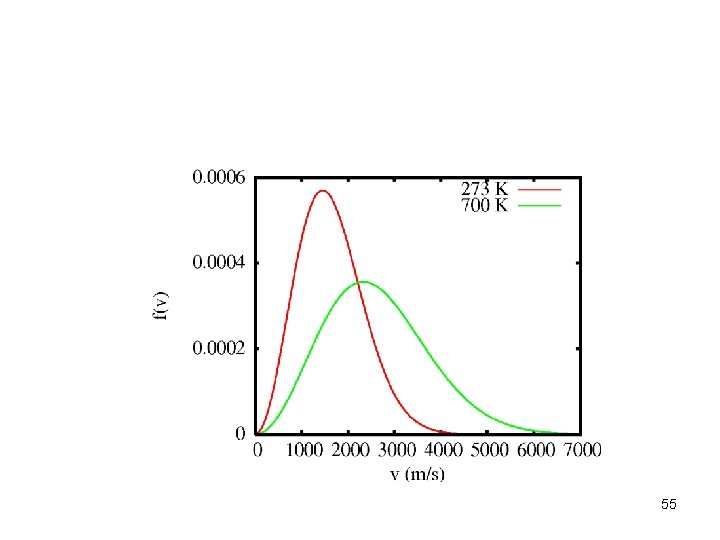
• Hydrogen, m=2 mp vmax = 1. 93 km / s 54

55

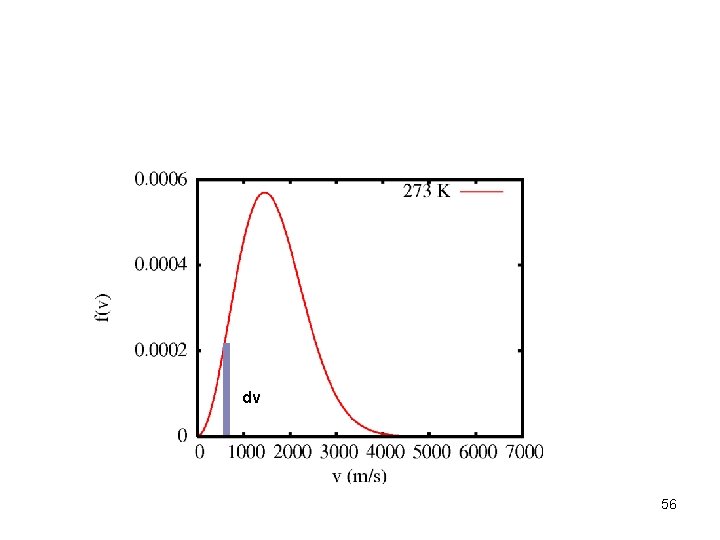
dv 56

Maxwell’s Demon 57

Stany czyste i stany mieszane (Pure and mixed states) Fizyka klasyczna: mikrostany układu to punkty x=(p, q) w 6 N wymiarowej przestrzeni fazowej, a wielkości mierzalne (obserwable) np. energia H(x), to funkcje na przestrzeni fazowej. Zbiór punktów fazowych układu z przypisanymi im prawdopodobieństwami tworzy statystyczny zespół fazowy, dla którego możemy wyznaczyć odpowiednie gęstości prawdopodobieństwa. Mechanika kwantowa: musimy rozróżnić stan układu ( wektor w przestrzeni Hilberta) czy funkcję falową będącą rzutem wektora stanu na odpowiednią bazę, od możliwych wyników pomiaru. 58

Quantum-mechanical description of the statistical systems. We have to distinguish between the state of the system: a vector in a Hilbert space |F> and the components of this vector with respect to some basis are the wavefunctions F(x), F(p), F(E): x, p, E form a complete set of quanyum numbers for a complete system of commuting observables→self-adjoint operators in the hlbert space, and their spectrum represents the possible results of measurement: positions, momenta, energies etc. 59

The density operator (density matrix) A pure state: if the system is in a definite state |Ψ(i’)> then p(i’)=1 and p(i)=0 otherwise. The statistical expectation value of A (<A>): 60

Properties of density operators. • • • Trρ=1; (A=1). The density opertor is hermitian. For every state |Ψ> in the Hilbert space - <Ψ|ρ|Ψ>≥ 0 since • The density operator satisfies Tr(ρ2)≤ 1, and Tr(ρ2)=1, if and only if ρ represents a pure state. 61

The entropy of a density operator. 62

Równanie von Neumanna (przybliżenie RPA (Random Phase Approximation 63

Identyczne cząstki kwantowe- statystyki kwantowe -Paczka falowa ma rozmiar przestrzenny: λ=h/p (de Broglie) -gaz w równowadze (ekwipartycja energii): p 2/2 m=3/2 k. T Stąd: λ=h/(3 mk. T)1/2. Termiczna długość fali pozwala oszacować rozmiar lokalizacji paczki falowej (ΔxΔp~ћ). • Szacowanie granica klasycznej i termicznej długości fali: Def. Używana w fizyce. statystycznej różni się o stałą: 64

65

• Układ klasyczny: λ<<średnia odległość międzycząstkowa~n 1/3 1. Opis klasyczny: 1. Opis kwantowy: 66

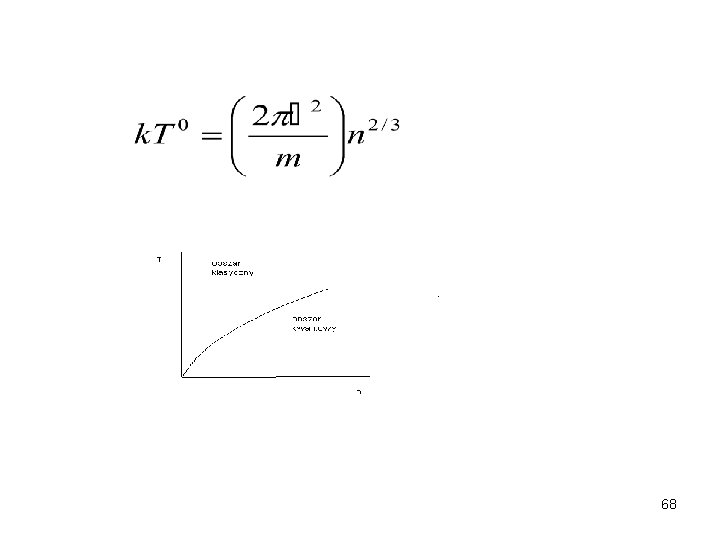
• Temperatura zwyrodnienia, to temparatura poniżej której istotne są efekty kwantowe → 67

68
![Przykładowe temperatury degeneracji kwantowej Układ Gęstośćcm 3 T 0K gazowy H 2 ciekły 4 Przykładowe temperatury degeneracji kwantowej Układ Gęstość[cm 3] T 0[K] gazowy H 2 ciekły 4](https://slidetodoc.com/presentation_image_h/fa6832bc4976189558ef37213dae7cfd/image-69.jpg)
Przykładowe temperatury degeneracji kwantowej Układ Gęstość[cm 3] T 0[K] gazowy H 2 ciekły 4 He el. w metalach 2 *1019 2*1022 5 *10 -2 2 104 69

Nierozróżnialność cząstek • • Hamiltonian układu czastek jest niezmienniczy względem permutacji P tzn. [P, H]=0 (PHP-1=H). Działanie P na stan (np. dwie cząstki): C=1 -bozony (symetryczna funkcja falowa C=-1 -fermiony (antysymetryczna funkcja falowa 70

C=1 -bozony (symetryczna funkcja falowa (statystyka Bosego_Einsteina), spin całkowity. C=-1 -fermiony (antysymetryczna funkcja falowa (statystyka Fermiego-Diraca), spin połówkowy. Orbitalny moment pędu cząstek nie zmienia statystyki. Dlaczego? 71

Reprezentacja liczby obsadzeń (the occupation number represemtation) • • Dla dowolnej liczby cząstek N funkcja falowa jest zdeterminowana odpowiednią kombinacją liniową iloczynów stanów jednocząstkowych: może być parzysta (dla bozonów) 72

• może być nieparzysta (dla fermionów) Wyznacznik Slatera: zapewnia zakaz Pauliego- ui (r)=u i(r) 73

Idealne układy kwantowe (Ideal quantum systems) (kolejność nieistotna) to znaczy, że wystarczy podać liczbę cząstek w stanie α: nα. Liczbę tę nazywamy liczbą obsady (obsadzenia) stanu jednocząstkowego α. Stan układu N cząstek może być określony przez podanie liczby cząstek nα, które znajdują się w stanie |α> Wartości liczby obsady dla bozonów i fermionów: • Funkcja falowa N cząstek jest numerowana zbiorem {α 1, …, αN} 74

• Fotony i fonony: ich liczba N w równowadze w zamknietej wnęce (krysztale) o objętości V i temperaturze T nie może być dowolna (ale mogą znikać i powstawać), jak w przypadku gazów cząsteczkowych, ale jest określona przez V i T. N jest określone z warunku minimum energii swobodnej F tzn. : µ-potencjał chemiczny 75

Suma stanów dla układu złożonego z N cząstek: Dla fotonów i fononów nie ma ograniczenia na N (µ=0). Jak można ominąć ograniczenie wynikające z liczby cząstek N i sumowania po stanach jednocząstkowych? Wprowadzamy wielki zespół kanoniczny, a stąd potencjał chemiczny, rezygnując z stałej liczby cząstek. Możemy to zrobić, ponieważ potencjał chemiczny możemy wyznaczyć z średniej liczby cząstek, którą za chwile obliczymy. Teraz enrgie jednoczastkowe liczone są względem potencjału chemicznego: εα->εα-µ. 76
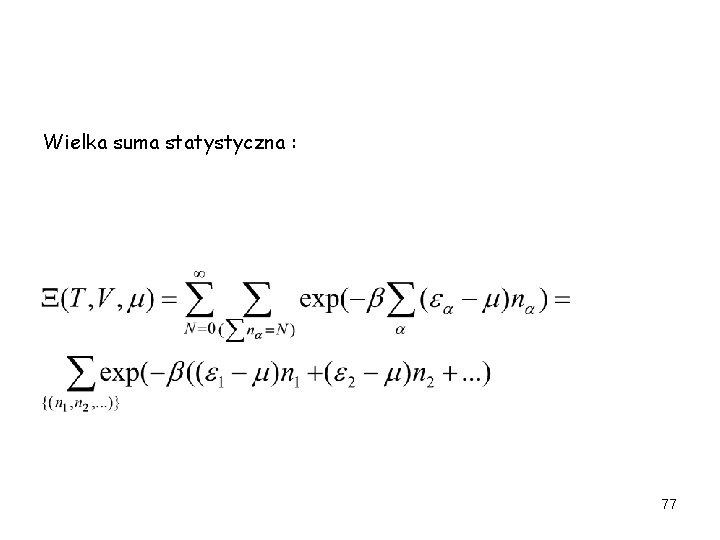
Wielka suma statystyczna : 77

Po przegrupowaniu zα-suma stanów dla stanu α; cząstki obsadzają każdy Stan α niezależnie. 78
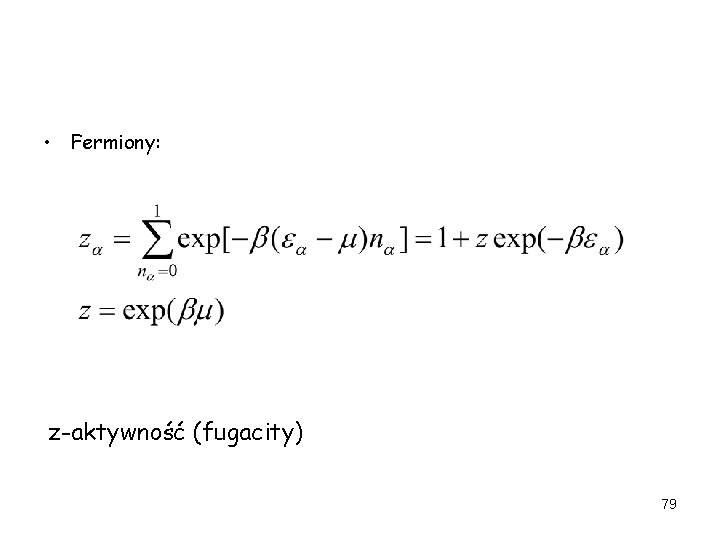
• Fermiony: z-aktywność (fugacity) 79

• Bozony: Dla bozonów µ<0 80

Średnia liczba cząstek w stanie α: Bozony-rozkład Bosego-Einsteina Fermiony- rozkład Fermiego-Diraca 81

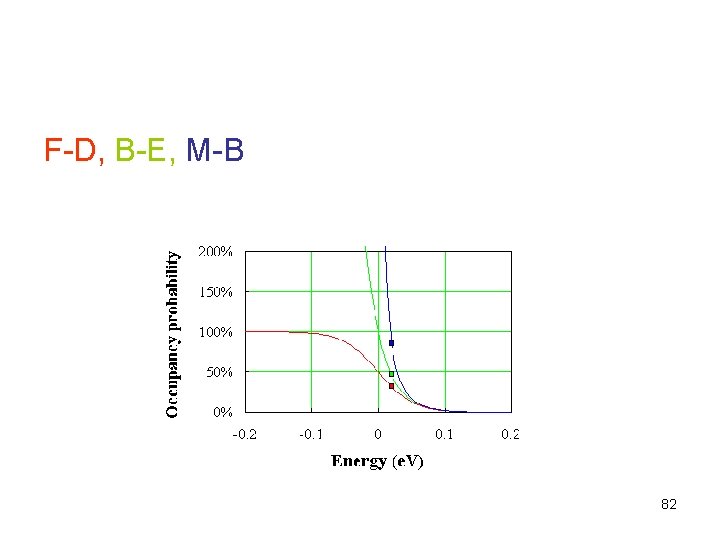
F-D, B-E, M-B 82

83

Wielka suma statystyczna Fermiony-znak górny; bozony- znak dolny Wielki potencjał termodynamiczny (potencjał termodynamiczny) 84

Granica klasyczna- rozkład Maxwella-boltzmanna Mała gęstośc cząstek: nα<<1 →z<<1→ można zaniedbac ± 1 w mianowniku: 85

Wartości średnie 86

Gazy doskonałe Stany jednoczastkowe |α>=|k, m>; m=1/2 lub -1/2 ( w jednostkach ћ) , a k jest wektorem falowym. Czynnik degeneracji g=2. ki=niπ/L (L-rozmiar układu w kierunku i-x, y, z) Suma po ki to suma po ni=ki. L/π=1, 2, … ρ- gęstośc stanów (DOS-Density of States) 87
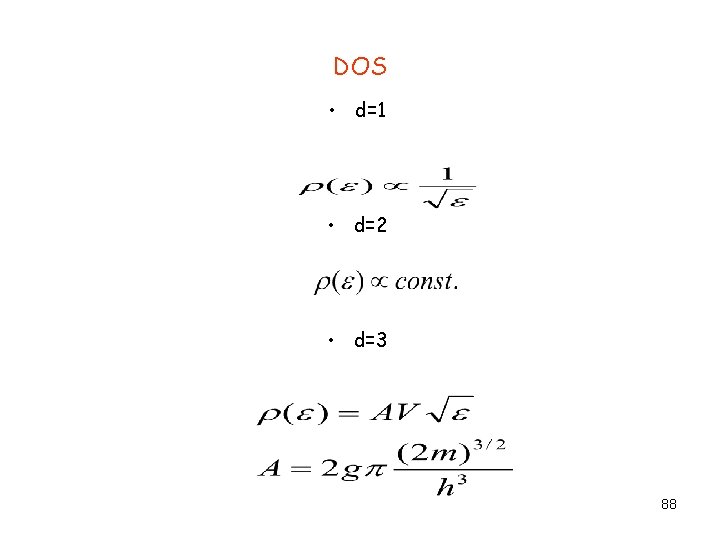
DOS • d=1 • d=2 • d=3 88

Po całkowaniu przez części 89

Fermiony stan podstawowy (T=0) µ(T=0)=EF • Energia • Liczba cząstek • Energia Fermiego 90

• Ciśnienie Dla fermionów ciśnienie w T=O jest różne od zera, ponieważ tylko dwa fermiony mogą miec zerowy pęd. Przykład: el. w metalu n=1022 cm-3 91

Bozony: Przydatne całki 92
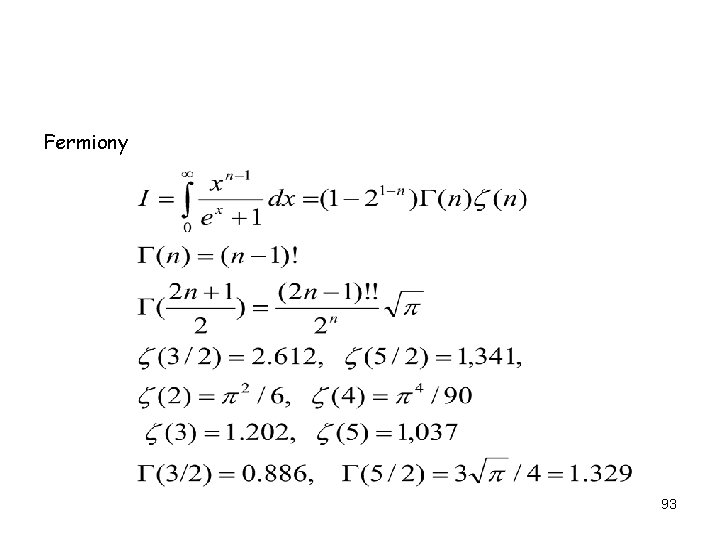
Fermiony 93

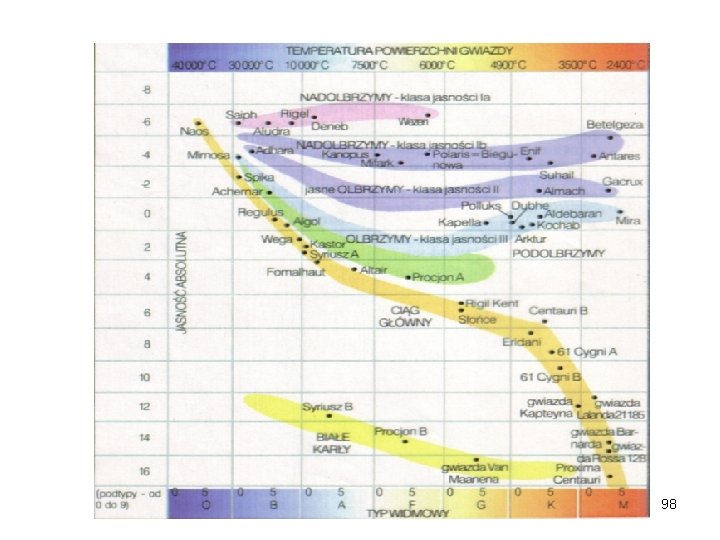
Przykłady zdegenerowanych układów fermionowych • Elektrony w metalach n=N/V=(1 -10)x 1022 cm-3, εF=(2 -8)e. V, TF=(2 -8)x 105. W temperaturze pokojowej T<<TF- elektrony tworzą silnie zdegnerowany gaz. • Białe karły (white dwarf stars) Masa porównywalna z masa Słońca, a promień rzędu promienia ziemi. Przykład: Syriusz B (towarzysz Syriusza) 94

Jeden atom wodoru zajmuje objętość 10 -10 m=0. 01Å. → atomy są zupełnie zjonizowane i elektrony tworzą gaz. Czy gaz ten jest zdegenerowany. W porównaniu z elektronami w metalu n jest 108 razy większe, a εF n 2/3~105 razy tzn. 95

Z obserwacji wiadomo, że temperatura wewnątrz Syriusza B wynosi T=107 K <<TF. Ciśnienie Pualiego elektronów nie kompensuje siły grawitacji→ grawitacyjne zapadanie (gravitational collapse) jeżeli przekroczona jest ranica Chandrasekhara: M gwiazdy>1. 4 M Słońca. Jądra (protony) w białych karłach nie tworzą gazu zdegenerowanego (m protonu wynosi w przyblizeniu 2000 masy elektronu). 96

• Gwiazdy neutronowe (neutron stars) W tych warunkach również jądra tworza gaz zdegenerowany 97

98

Statystyki Fermiego-Diraca i Bosego-Einsteina (c. d. ) Gęstość cząstek 99
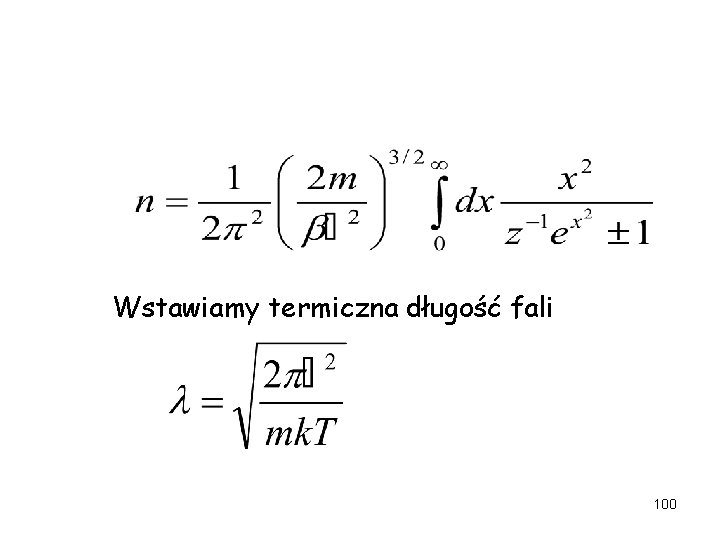
Wstawiamy termiczna długość fali 100
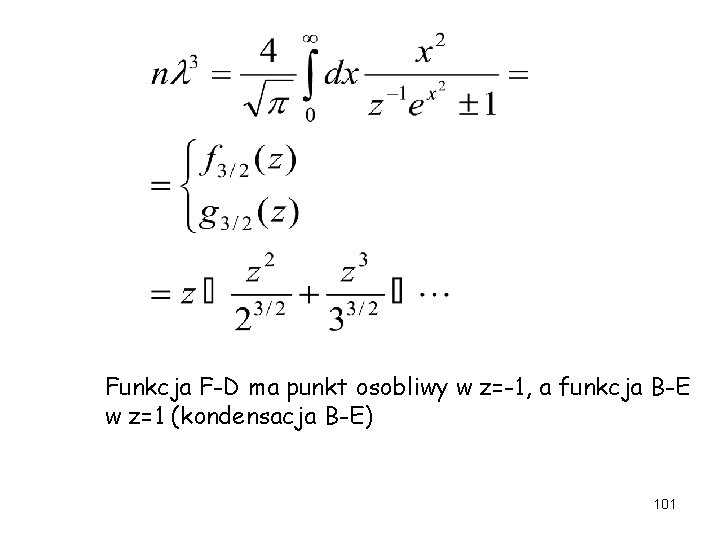
Funkcja F-D ma punkt osobliwy w z=-1, a funkcja B-E w z=1 (kondensacja B-E) 101

Przydatne funkcje i relacje 102
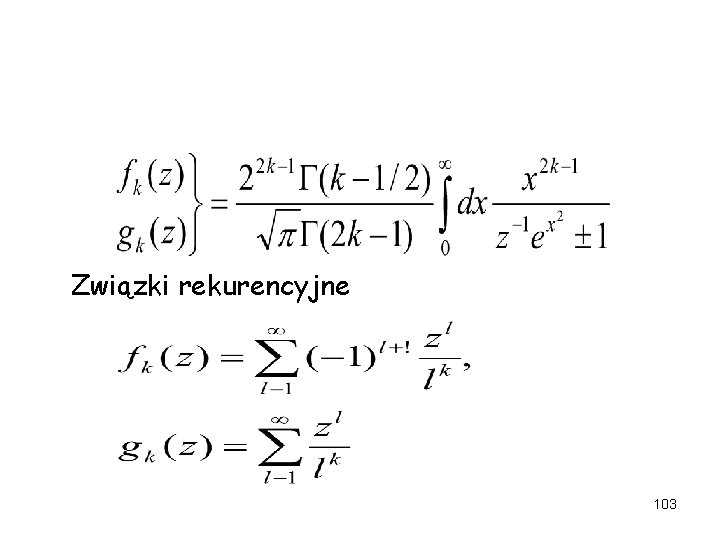
Związki rekurencyjne 103

Kondensacja Bosego-Einsteina Bose-Einstein condensation 104
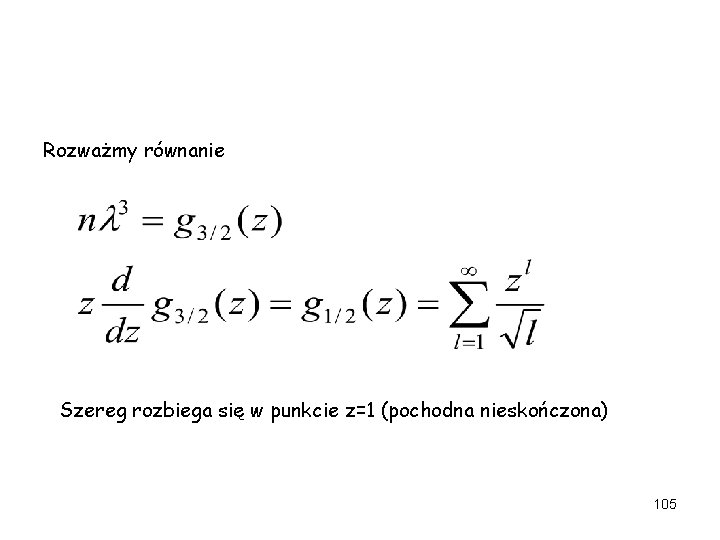
Rozważmy równanie Szereg rozbiega się w punkcie z=1 (pochodna nieskończona) 105

Górne ograniczenie na g 3/2 Gdy nλ 3 osiąga tę wartość, cząstki przechodzą do stanu o zerowym pędzie (energii). Prowadzi to kondensacji B-E. Kondensat składa się z cząstek ozerowym pędzie. Podczas kondensacji aktywność jest Równa 1 (µ=0). 106

Granica pomiędzy faza gazową a skondensowaną 107

Temperatura i gęstość krytyczna 108
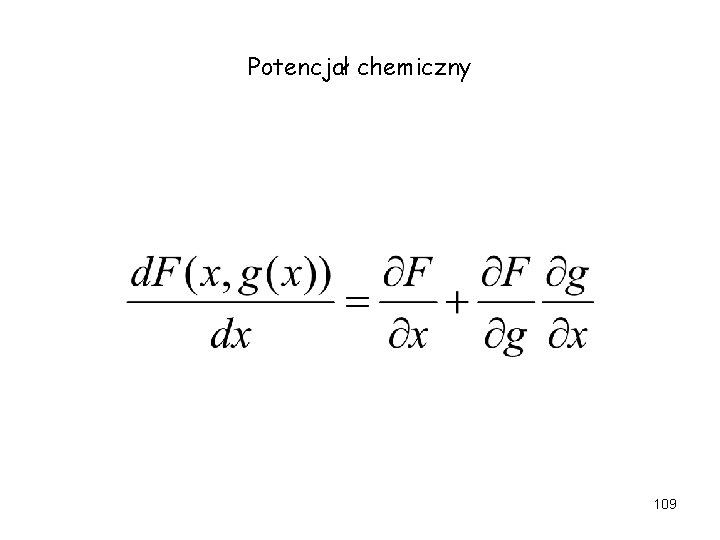
Potencjał chemiczny 109

b-e-cond 2. pdf 110

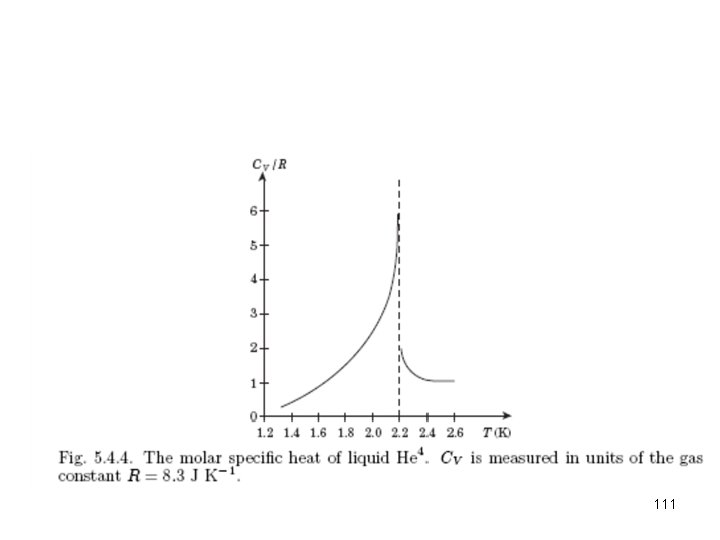
111

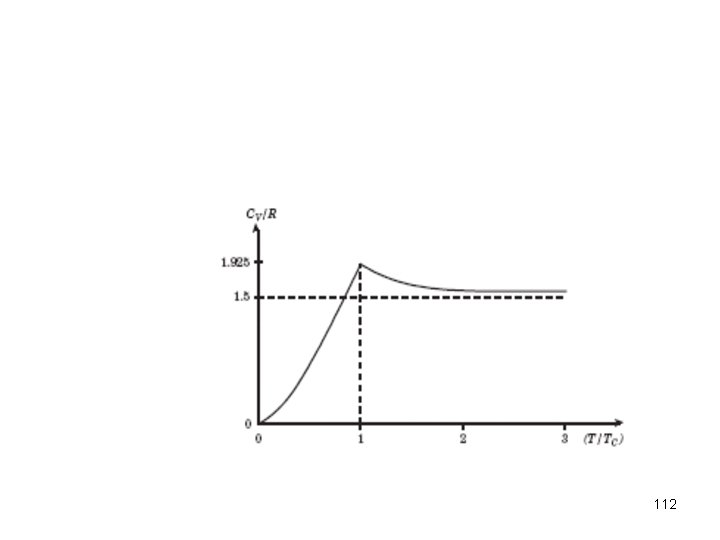
112

Przejścia fazowe: fiz-stat-phase-transit 1 113

Przejścia fazowe • Przejścia fazowe nieciągłe (pierwszego rodzaju): gaz-ciecz • Przejścia ciągłe (drugiego rodzaju): ferrro-paramagneyk, nadprzewodnikstan normalny, gaz-ciecz w punkcie krytycznym) 114

• Równanie stanu jest funkcją regularną (analityczną) w każdej fazie: ciągłą o ciągłych pochodnych. Przy przejściu z jednej fazy do drugiej równanie stanu przechodzi (w różny sposób dla przejść ciągłych i nieciągłych) w inną regularną funkcję. Przejścia nieciągłe: pierwsza pochodna potencjału (Gibbsa) jest nieciągła na granicy pomiędzy fazami 115

Przejścia nieciągłe: pierwsza pochodna potencjału G (Gibbsa) jest nieciągła na granicy pomiędzy fazami →np. nieciągłość gęstości i entropii (patrz r. Maxwella: ) • Ciepło utajone (ciepło przemiany): współistniejące fazy mają różne entropie → układ musi pochłaniać lub oddawać ciepło podczas przemiany fazowej Q=T 0(S 2 -S 1), T 0 -temperatura, w której współistnieją fazy, S 1(2) entropia 1(2) fazy; • Punkt krytyczny: w punkcie krytycznym gęstość i entropia gazu i cieczy są jednakowe → przejście fazowe ciągłe (drugiego rodzaju) • Punkt potrójny: punkt współistnienie trzech faz: ciekłej, gazowej, stałej. 116

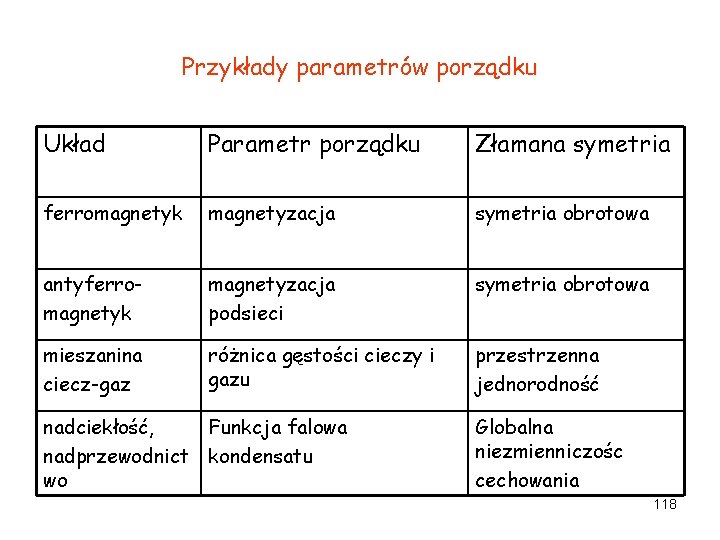
pierwsze pochodne potencjału na granicy faz są ciągłe, a drugie pochodne są nieciągłe Przejścia ciągłe: • Parametr porządku: wielkość, która równa się zero powyżej temperatury Tc krytycznej i jest różna od zero poniżej Tc. Przejście ciągłe, to przejście łamiące symetrię. Przykłady parametru porządku: 117

Przykłady parametrów porządku Układ Parametr porządku Złamana symetria ferromagnetyk magnetyzacja symetria obrotowa antyferromagnetyk magnetyzacja podsieci symetria obrotowa mieszanina ciecz-gaz różnica gęstości cieczy i gazu przestrzenna jednorodność nadciekłość, Funkcja falowa nadprzewodnict kondensatu wo Globalna niezmienniczośc cechowania 118

Spontaniczne łamanie symetrii • Fizyczna przyczyna: oddziaływanie np. w ferromagnetykupowoduje równoległe ustawienie spinów (złamana symetria rotacyjna hamiltonianu) obniżające energię wewnętrzna układu U. Przeciwdziałają temu fluktuacje termiczne, które zwiększają entropię układu S. Prowadzi to do zerowania (minimalizacji) energii swobodnej F=U-TS. • Na ogół w niskich temperaturach materia ma inną symetrię niż tworzące je składniki (np. atomy w kryształach, gdzie złamana niezmienniczość translacyjna hamiltonianu wynikająca z jednorodności przestrzennej). • Gdy hamiltonian jest niezmienniczy ze względu na pewne operacje symetrii, a stan podstawowy nie jest niezmienniczy, to mówimy, że symetria została złamana spontanicznie 119

Zmiana stanu |ψ> pod wpływem operacji symetrii P H |ψ> =E |ψ> ; niezmienniczość [H, P]=0, P-1 HP=H. Z tego wynika, że P-1 HP |ψ> =E |ψ> oraz HP |ψ> =E P|ψ> Wniosek: Jeżeli P|ψ> jest innym stanem niż |ψ>, to obydwa stany są Równoprawnymi stanami podstawowymi, a to oznacza, ze jeżeli symetria jest złamana (spontanicznie), to stan podstawowy jest zdegenerowany. W ferromagnetyku degeneracja może by nieskończona. Przejście od jednej konfiguracji do drugiej wymaga energii (występuje bariera energetyczna). W miarę zbliżania się do punktu krytycznego obszary uporządkowane rozrastają się (rośnie promień korelacji; w TC jest nieskończony) i coraz dłużej trwa odwrócenie konfiguracji (krytyczne spowolnienie ang. critical slowing down→ dynamiczny indeks krytyczny z). Układ przestaje być ergodyczny (nie są dostępne wszystkie punkty przestrzeni spinów (przestrzeni fazowej); separowalnośc metryczna przestrzeni fazowej. 120

Model Isinga Energia E konfiguracji {s} w polu magnetycznym h: S=± 1, w D wymiarowej przestrzeni; (i, j)- para najbliższych sąsiadów; {s}={s 1, s 2, …, s. N}- konfiguracja N spinów; J- stała oddziaływania (całka (parametr) wymiany) 121

Magnetyzacja M(h) (parametr porządku) (β=1/k. T) Dla h=0 E{s}=E{-s} i M(0)=-M(0), a to znaczy M(0)=0 → paradoks: brak magnetyzacji. Wyjaśnienie paradoksu: W granicy termodynamicznej: N→∞ (N/V=constans) i Dostatecznie niskich T układ nie może przejść w skończonym czasie przez wszystkie dostępne konfiguracje oznacza to że: 122

Granice N→∞ i h→ 0 nie komutują tzn. : Druga granica prowadzi do spontanicznego złamania symetrii 123

Hipoteza skalowania Widoma i Kadanoffa • Zachowanie układu w pobliżu punktu krytycznego (w obszarze krytycznym) nie zalaży od mikroskopowych własności układu (np. oddziaływania), ale od wymiaru układu i wymiaru parametru porządku 124
 Prawdopodobieństwo termodynamiczne
Prawdopodobieństwo termodynamiczne Generalizacja statystyczna
Generalizacja statystyczna Statystyczna karta wypadku doc
Statystyczna karta wypadku doc Shutter
Shutter Katedra fizyki prz
Katedra fizyki prz Praw fizyki pan nie zmienisz
Praw fizyki pan nie zmienisz Strefa otwartej nauki pwr
Strefa otwartej nauki pwr Zakład fizyki nanostruktur i nanotechnologii uj
Zakład fizyki nanostruktur i nanotechnologii uj Instytut fizyki umk
Instytut fizyki umk Koszykowa 75 warszawa
Koszykowa 75 warszawa Maszyny proste przykłady
Maszyny proste przykłady The talent show by susan wojciechowski
The talent show by susan wojciechowski The talent show by susan wojciechowski
The talent show by susan wojciechowski Piotr wojciechowski pwr
Piotr wojciechowski pwr Statistical physics
Statistical physics Statistical physics quiz
Statistical physics quiz Fizyka
Fizyka Fizyka
Fizyka Umk fizyka
Umk fizyka Obrazy w soczewkach prezentacja
Obrazy w soczewkach prezentacja Fizyka techniczna pk
Fizyka techniczna pk Mikrofale fizyka
Mikrofale fizyka Sylwester kalinowski fizyka
Sylwester kalinowski fizyka Jednostki fizyka
Jednostki fizyka Jednostka kąta bryłowego
Jednostka kąta bryłowego Fizyka
Fizyka Fizyka
Fizyka Praca moc energia prezentacja
Praca moc energia prezentacja Zuzanna majewska
Zuzanna majewska Fizyka kwantowa podstawy
Fizyka kwantowa podstawy Wzór einsteina millikana
Wzór einsteina millikana Moc jednostka
Moc jednostka Podstawa programowa fizyka
Podstawa programowa fizyka Mgcosa
Mgcosa Zachodzące w powietrzu otaczającym kulę ziemską
Zachodzące w powietrzu otaczającym kulę ziemską Praca jednostka fizyka
Praca jednostka fizyka Energia potencjalna
Energia potencjalna Obraz pozorny
Obraz pozorny Masa w układzie si
Masa w układzie si Zastosowanie zjawiska fotoelektrycznego zewnętrznego
Zastosowanie zjawiska fotoelektrycznego zewnętrznego Dziekuje za uwage fizyka
Dziekuje za uwage fizyka Fizyka
Fizyka Fizyka atomowa
Fizyka atomowa Budowa mikrofonu fizyka
Budowa mikrofonu fizyka 2 zasada dynamiki
2 zasada dynamiki I zasada termodynamiki
I zasada termodynamiki Obrazy tworzone przez soczewki
Obrazy tworzone przez soczewki Silniki cieplne
Silniki cieplne Umk fizyka
Umk fizyka Opory ruchu fizyka
Opory ruchu fizyka Ryszard bugajski
Ryszard bugajski Ryszard walkowiak
Ryszard walkowiak „polska” – ryszard przymus.
„polska” – ryszard przymus. Piotr pietraszek pwr
Piotr pietraszek pwr Ośrodek mowy w mózgu
Ośrodek mowy w mózgu Ostatni hippis naszych czasów
Ostatni hippis naszych czasów Ryszard dobrołowicz
Ryszard dobrołowicz Ryszard jadach
Ryszard jadach Pozycja średnia klappa
Pozycja średnia klappa Małgorzata pol
Małgorzata pol Pozycja wykroczna
Pozycja wykroczna Ryszard szarfenberg
Ryszard szarfenberg Ryszard siwiec
Ryszard siwiec Kartodiagram słupkowy
Kartodiagram słupkowy Pregiel
Pregiel Ryszard przymus wikipedia
Ryszard przymus wikipedia Emmanuelle walkowiak
Emmanuelle walkowiak Ib physics doc
Ib physics doc Why does it happen
Why does it happen University physics with modern physics fifteenth edition
University physics with modern physics fifteenth edition Statistical inference
Statistical inference 20%ของ300
20%ของ300 Chebyshev's inequality
Chebyshev's inequality Dulong petit law
Dulong petit law Misleading graphs
Misleading graphs Statistical business register
Statistical business register Statistical graphics
Statistical graphics Generating alpha meaning
Generating alpha meaning Statistical parametric mapping software
Statistical parametric mapping software Stat
Stat Statistical forecasting models
Statistical forecasting models Statistical displays
Statistical displays Jmp vs spss
Jmp vs spss Features of quantitative research
Features of quantitative research Mssc introduction to spc
Mssc introduction to spc Statistical techniques in robotics
Statistical techniques in robotics Statistical average crossword
Statistical average crossword Null hypothesis example
Null hypothesis example Gsi
Gsi Partition function in statistical mechanics
Partition function in statistical mechanics Evaluation of statistical infrequency
Evaluation of statistical infrequency Six sigma statistical tools
Six sigma statistical tools Gibbs free energy
Gibbs free energy Statistical forecasting techniques
Statistical forecasting techniques Statistical model for crd
Statistical model for crd Statistical jargon
Statistical jargon Statistical package for the social sciences
Statistical package for the social sciences Statistical investigation examples
Statistical investigation examples Introduction to quantum statistical mechanics
Introduction to quantum statistical mechanics Statistical pattern recognition a review
Statistical pattern recognition a review Retire statistical significance
Retire statistical significance What is microcanonical ensemble
What is microcanonical ensemble Statistical data warehouse
Statistical data warehouse Gdp expenditure approach formula
Gdp expenditure approach formula Characteristics of statistical unit
Characteristics of statistical unit Testing of hypothesis
Testing of hypothesis Statistical language models for information retrieval
Statistical language models for information retrieval Advanced and multivariate statistical methods
Advanced and multivariate statistical methods Multilevel multiplexing
Multilevel multiplexing Statistical mechanics
Statistical mechanics Statistical investigation process
Statistical investigation process Statistical process control tutorial
Statistical process control tutorial Statistical process control
Statistical process control 12000x12
12000x12 Bp statistical review of world energy 2009
Bp statistical review of world energy 2009 Evan miller calculator
Evan miller calculator Primer statistical software
Primer statistical software Rafael perera
Rafael perera Statistical symbols and meanings
Statistical symbols and meanings Strengths and weaknesses of statistical infrequency
Strengths and weaknesses of statistical infrequency Statistical business analysis
Statistical business analysis Generic statistical business process model
Generic statistical business process model Statistical language models for information retrieval
Statistical language models for information retrieval Statistical quality control in operations management
Statistical quality control in operations management Statistical based ids
Statistical based ids