FIZIKAnauka o najoptijim svojstvima i formama kretanja materije

FIZIKA-nauka o najopštijim svojstvima i formama kretanja materije Prof. Dr Slavoljub Mijović Prirodno-matematički fakultet Podgorica e-mail: slavom@ucg. ac. me smijovic@yahoo. com 069374734

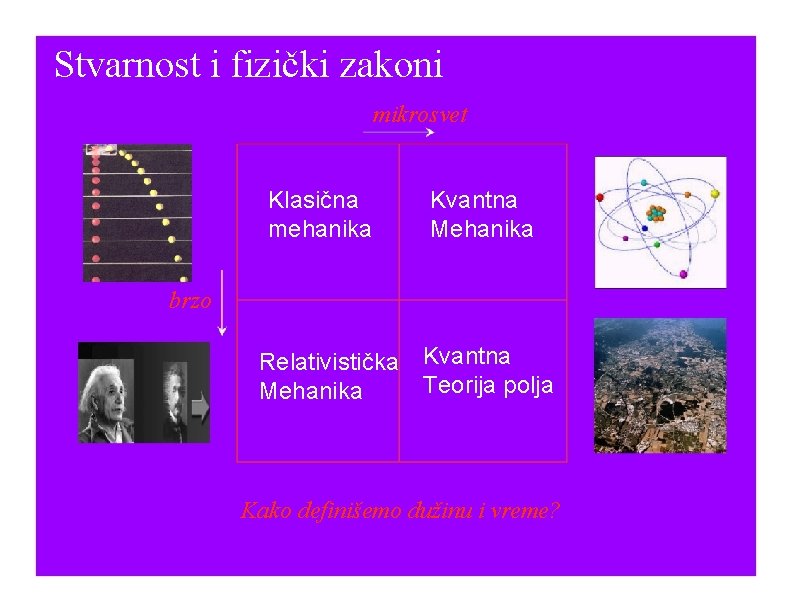
Stvarnost i fizički zakoni mikrosvet Klasična mehanika Kvantna Mehanika brzo Relativistička Mehanika Kvantna Teorija polja Kako definišemo dužinu i vreme?

Mehanika • Mehaničko kretanje je najprostije kretanje materije, koje se sastoji u premeštanju tela ili njihovih delova jedno u odnosu na drugo. • Mehanički sistemukupnost tela izdvojenih za razmatranje • Referentni sistem je ukupnost medjusobno nepokretnih tela u odnosu na koja se razmatra kretanje i odgovarajućeg časovnika uprošćavanje, elastično ili tvrdo telo, materijalna tačka!

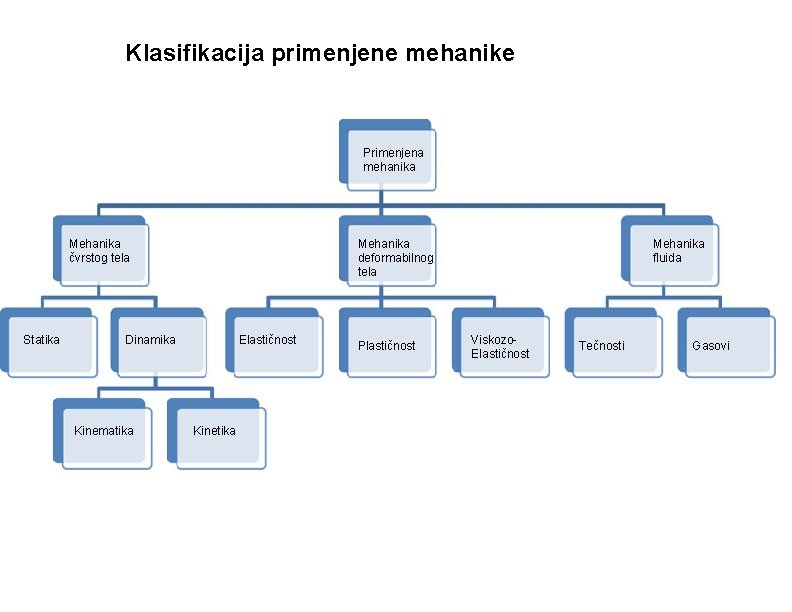
Klasifikacija primenjene mehanike Primenjena mehanika Mehanika čvrstog tela Statika Mehanika deformabilnog tela Dinamika Kinematika Elastičnost Kinetika Plastičnost Mehanika fluida Viskozo. Elastičnost Tečnosti Gasovi

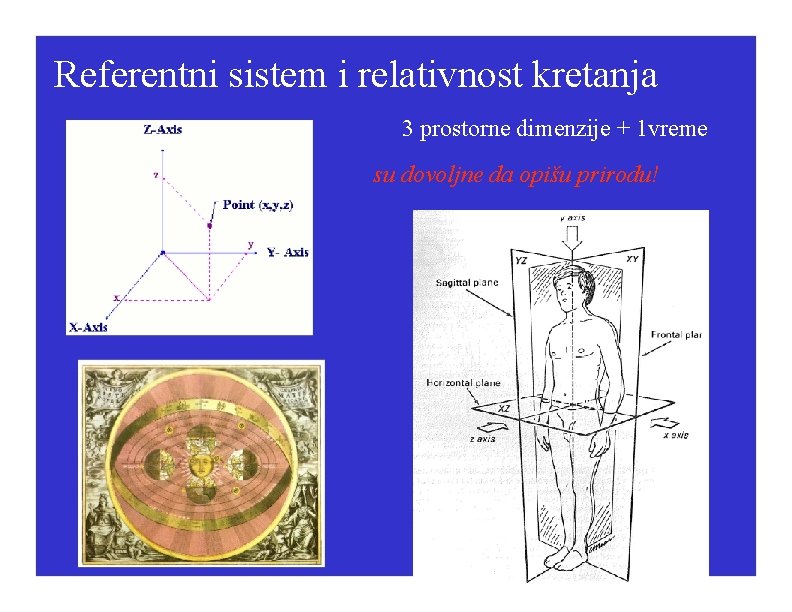
Referentni sistem i relativnost kretanja 3 prostorne dimenzije + 1 vreme su dovoljne da opišu prirodu!

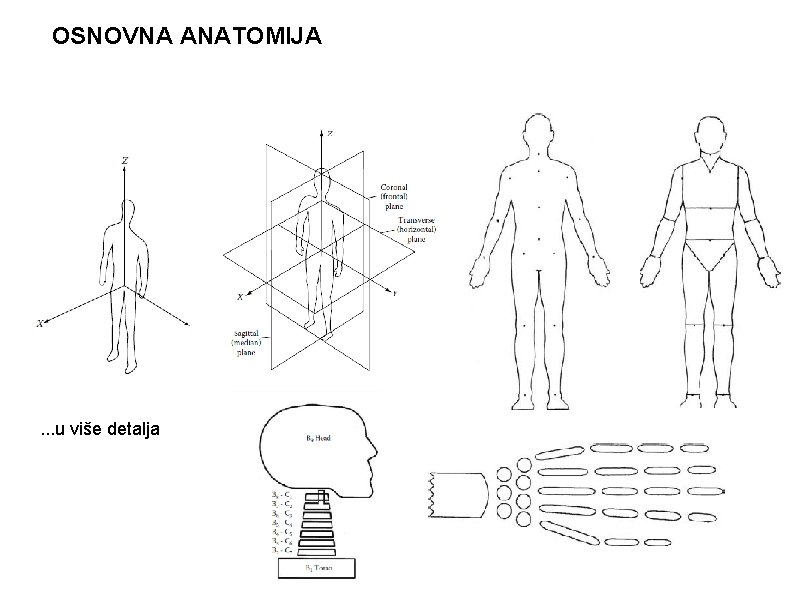
OSNOVNA ANATOMIJA . . . u više detalja

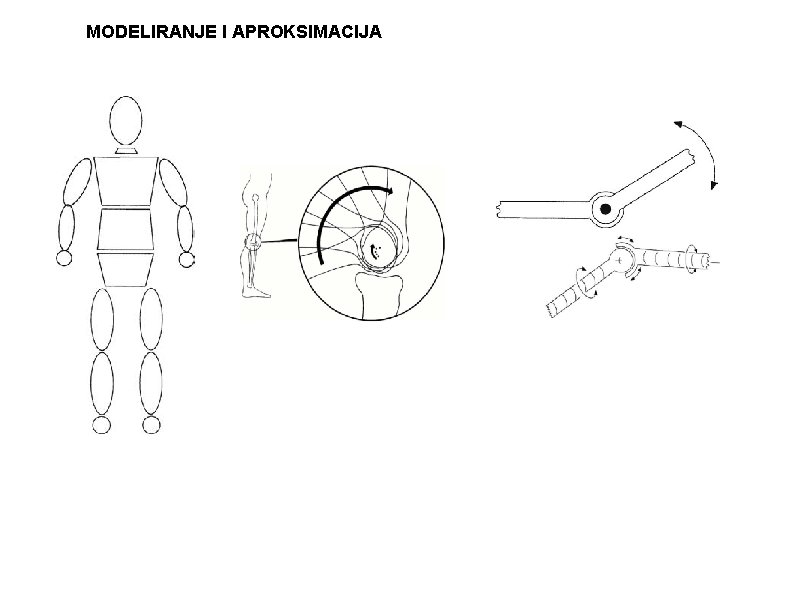
MODELIRANJE I APROKSIMACIJA

MODELIRANJE I APROKSIMACIJA

Ali. . . postoji li još prostornih dimenzija? U našem svakidašnjem svetu ona je nepotrebna!

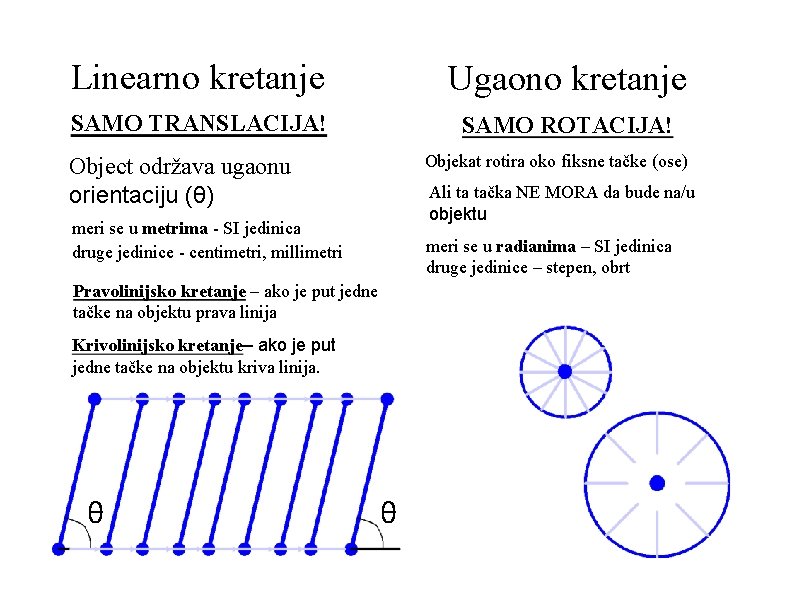
Linearno kretanje Ugaono kretanje SAMO TRANSLACIJA! SAMO ROTACIJA! Objekat rotira oko fiksne tačke (ose) Object održava ugaonu orientaciju (θ) Ali ta tačka NE MORA da bude na/u objektu meri se u metrima - SI jedinica druge jedinice - centimetri, millimetri meri se u radianima – SI jedinica druge jedinice – stepen, obrt Pravolinijsko kretanje – ako je put jedne tačke na objektu prava linija Krivolinijsko kretanje– ako je put jedne tačke na objektu kriva linija. θ θ

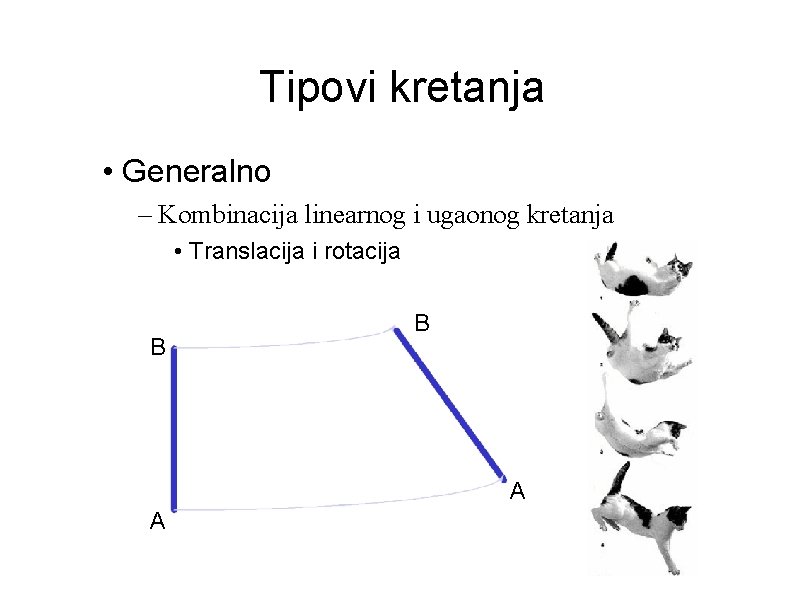
Tipovi kretanja • Generalno – Kombinacija linearnog i ugaonog kretanja • Translacija i rotacija B B A A

Stepeni slobode Jedan objekat u prostoru ima šest stepeni slobode kretanja. • Translacija – kretanje duž X, Y, i Z osa (tri stepena slobode) • Rotacija – rotira oko X, Y, i Z osa (tri stepeba slobode)

Stepeni slobode Ravan (2 D) mehanizam Stepeni slobode– broj nezavisnih koordinata potrebnih za kompletno određivanje pozicije objekta. Tri nezavisne kordinate su potrebne za određivanje lokacije objekta. AB, x. A, y. A, i ugao θ Nefiksirani objekat u ravni ima tri stepena slobode a i mehanizam povezan sa njim imaće takođe tri stepena slobode objekat

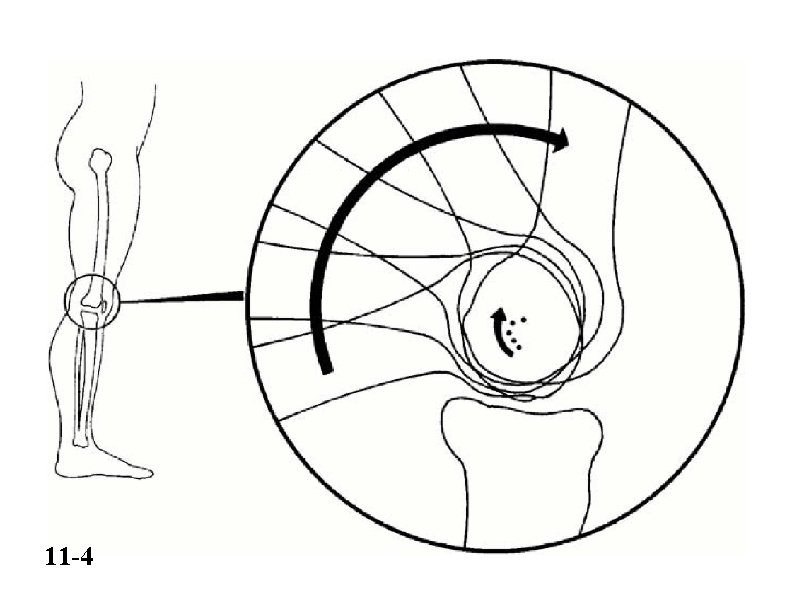
11 -4

Fizika & Kinematika • Veličine • Brzina • Jedinice • Ubrzanje (akceleracija) • Vektori • Kinematika • Pomeraj • Grafici kretanja u 1 -D (dimenziji)

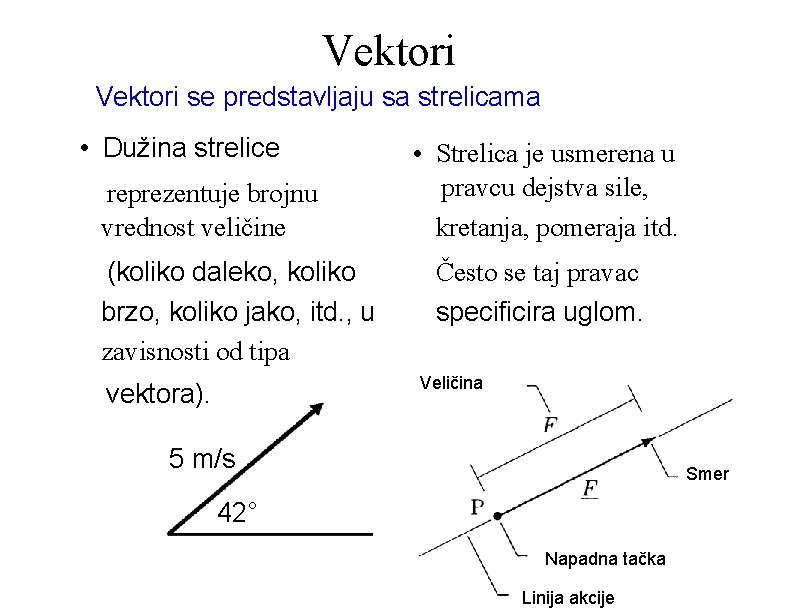
Neke fizičke veličine Vektor – veličina sa tri karakteristike: brojna vrednost, pravac i smer; Skalar – veličina koja se karakteriše samo sa brojnom vrednošću Merljive i objektivne! Vektori: • Pomeraj • Brzina • Ubrzanje • Impuls • Sila Skalari: • Rastojanje • Masa • Vreme • Enegija • Temperatura

Masa nasuprot gravitacije i težine Masa • Skalar (nema pravca) • Meri količinu materije u nekom objektu Gravitacija • Vektor (usmeren ka centru Zemlje) • Sila gravitacije na nekom objektu Težina • Sila kojom objekat pritiska podlogu Na Mesecu, tvoja masa će biti ista ali će mesečeva gravitacija biti manja i samim tvoja težina takođe.

Vektori se predstavljaju sa strelicama • Dužina strelice reprezentuje brojnu vrednost veličine (koliko daleko, koliko brzo, koliko jako, itd. , u zavisnosti od tipa • Strelica je usmerena u pravcu dejstva sile, kretanja, pomeraja itd. Često se taj pravac specificira uglom. Veličina vektora). 5 m/s Smer 42° Napadna tačka Linija akcije

Jedinice nisu isto što i veličine! Veličina. . . Jedinica (simbol) • Pomeraj & Rastojanje. . . metar (m) • Vreme. . . sekunda (s) • Brzina. . . (m/s) • Ubrzanje. . . (m/s 2) • Masa. . . kilogram (kg) • Impuls. . . (kg·m/s) • Sila. . . Njutn (Newton) (N) • Energija. . . Džul (Joule) (J)

Jedinice rotacionog kretanja • Pun ugao (krug) je 2πrad • 360 stepeni je jedan obrt • Radijan: ugao koji uključuje luk kružnice koji je jednak poluprečniku iste te kružnice • 1 obrt = 360 stepeni = 2 π radijana • 1 Radijan = 57. 3 stepeni • Konverzija iz stepena u rad – pomnožiti sa π/180 • Konverzija iz rad u stepen – pomnožiti sa 180/ π

SI Prefiksi Mali Veliki pico p 10 -12 nano 10 -9 10 -6 giga G 10 -3 tera T 10 -2 n micro µ milli m centi c kilo mega k M 10 3 10 6 10 9 10 12

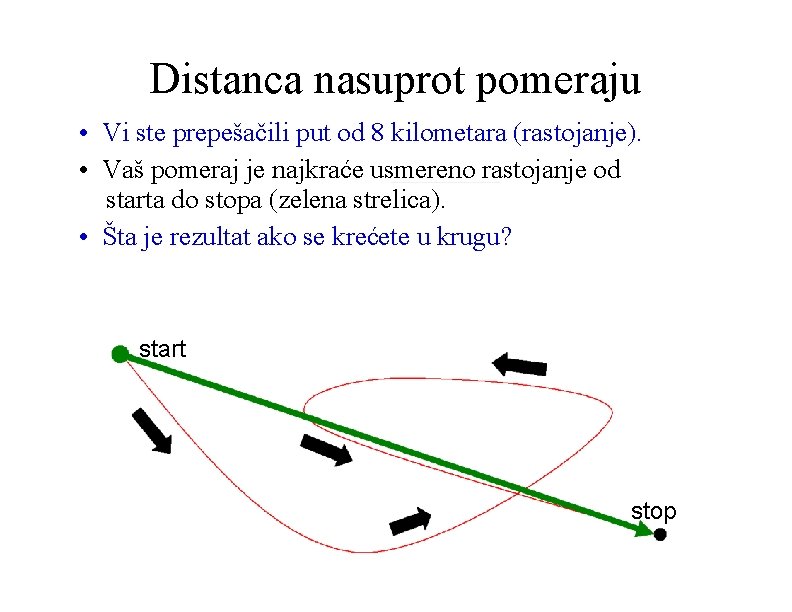
Kinematske definicije • Kinematika – grana fizike; izučavanje kretanja; • Pozicija (x) – gde se nalazi objekat; • Distanca (rastojanje) (d ) – koliko si putovao, nezavisno od pravca; • Pomeraj (∆x) – gde si u odnosu na start.

Distanca nasuprot pomeraju • Vi ste prepešačili put od 8 kilometara (rastojanje). • Vaš pomeraj je najkraće usmereno rastojanje od starta do stopa (zelena strelica). • Šta je rezultat ako se krećete u krugu? start stop

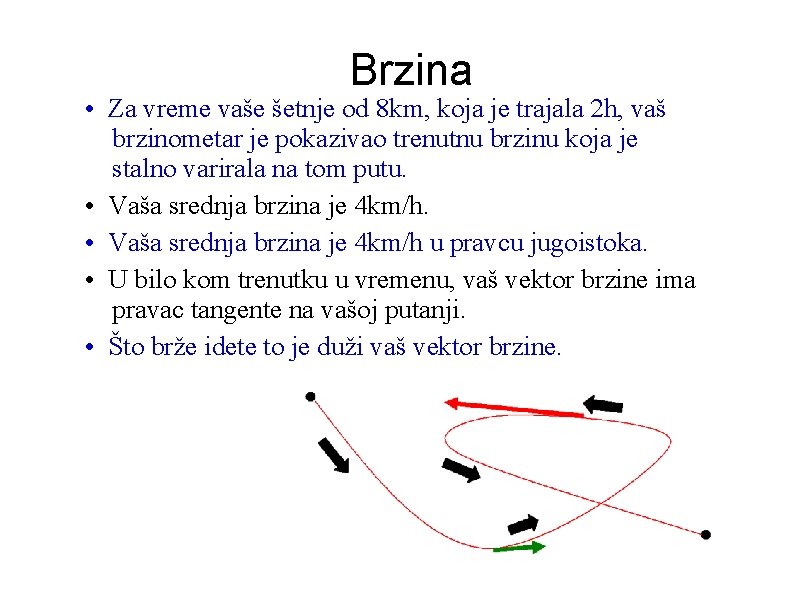
Brzina & Ubrzanje Brzina (v) – koliko brzo i kojim putem; mera za promenu pozicije objekta • Srednja brzina ( v ) – rastojanje/vreme • Ubrzanje (a) –kako se brzina uvećava, smanjuje ili menja pravac; odslikava brzinu promene brzine!

Moduo brzine • (koliko brzo se kreće neki objekat nezavisno od pravca i smera). Npr: v = 20 km/h • Moduo brzine je njena vrednost. • Brzina je vektor! Npr: v = 20 km/h i 15° jugozapadno. • Simbol za moduo brzine je Iv. I ili prosto v. Simbol za brzinu kao vektor je boldovano v ili sa strelicom iznad v

Brzina • Za vreme vaše šetnje od 8 km, koja je trajala 2 h, vaš brzinometar je pokazivao trenutnu brzinu koja je stalno varirala na tom putu. • Vaša srednja brzina je 4 km/h u pravcu jugoistoka. • U bilo kom trenutku u vremenu, vaš vektor brzine ima pravac tangente na vašoj putanji. • Što brže idete to je duži vaš vektor brzine.

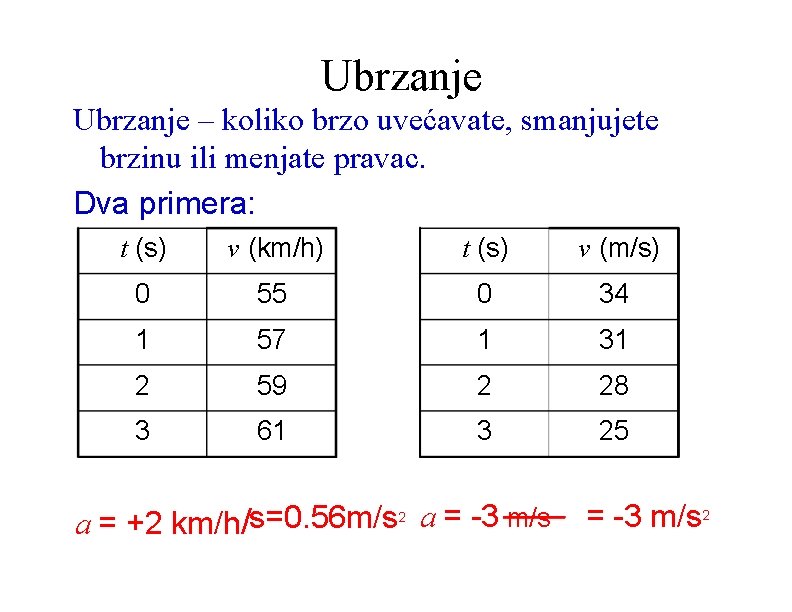
Ubrzanje – koliko brzo uvećavate, smanjujete brzinu ili menjate pravac. Dva primera: t (s) v (km/h) t (s) v (m/s) 0 55 0 34 1 57 1 31 2 59 2 28 3 61 3 25 a = +2 km/h/s=0. 56 m/s 2 a = -3 m/s 2

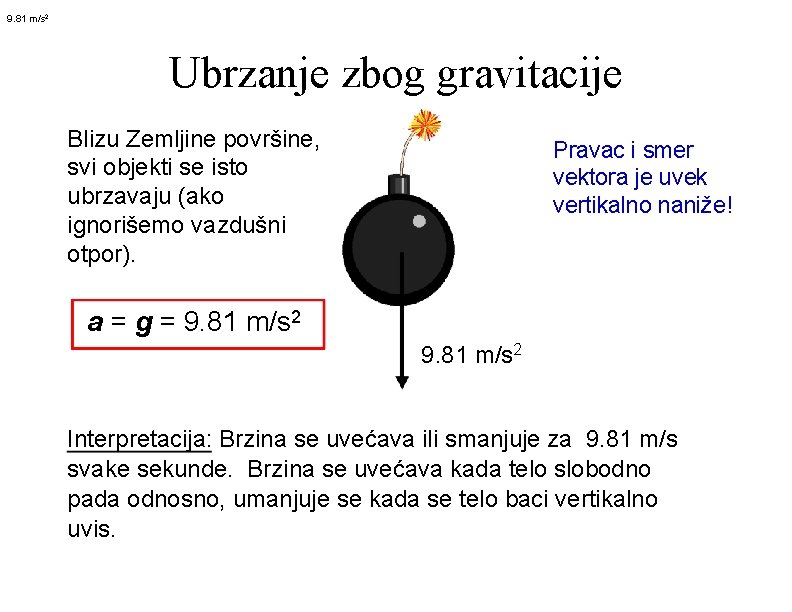
9. 81 m/s 2 Ubrzanje zbog gravitacije Blizu Zemljine površine, svi objekti se isto ubrzavaju (ako ignorišemo vazdušni otpor). Pravac i smer vektora je uvek vertikalno naniže! a = g = 9. 81 m/s 2 Interpretacija: Brzina se uvećava ili smanjuje za 9. 81 m/s svake sekunde. Brzina se uvećava kada telo slobodno pada odnosno, umanjuje se kada se telo baci vertikalno uvis.

Kinematske formule translatornog jednako ubrzanog kretanja Za 1 -D kretanje sa konstantnim ubrzanjem: • v k = v 0 + at v 0 vk x • v = (v 0 + v k)/2 • ∆x = v 0 t + ½ 1 2 at 2 • v k 2 – v 02 = 2 a x (izvođenja slede)

Izvođenja u kinematici a = v / t (definicija) a = (vk – v 0)/ t vk = v 0 + a t v vk v v 0 t v = (v 0 + vk )/2 dokazaćemo sa grafika. avg ∆x = v t = ½ (v 0 + vk) t = ½ (v 0 + a t) t x = v 0 t + 1 a t 2 2 (nastavak

Kinematska izvođenja (nast. ) ⇒ vk = v 0 + a t x = v 0 t + 1 at 2 2 t = (vk – v 0)/ a ⇒ x = v 0 [(vk – v 0)/ a] +1 a [(vk – v 0)/ a] 2 2 ⇒ vk 2 – v 02 = 2 a x Notirati da je jednačina na vrhu rešena po t i tada se izraz za t zamenio dvaput (u crvenom) u jednačini za x. Sve algebarske operacije treba izvršiti da bi se dobio finalni rezultat!. . I Domaći

Ako želite znati rastojanje koje ste prešli Distanca Brzina = Vreme Vi možete transformisati gornju jednačinu kao: Distanca = Brzina ⋅Vreme

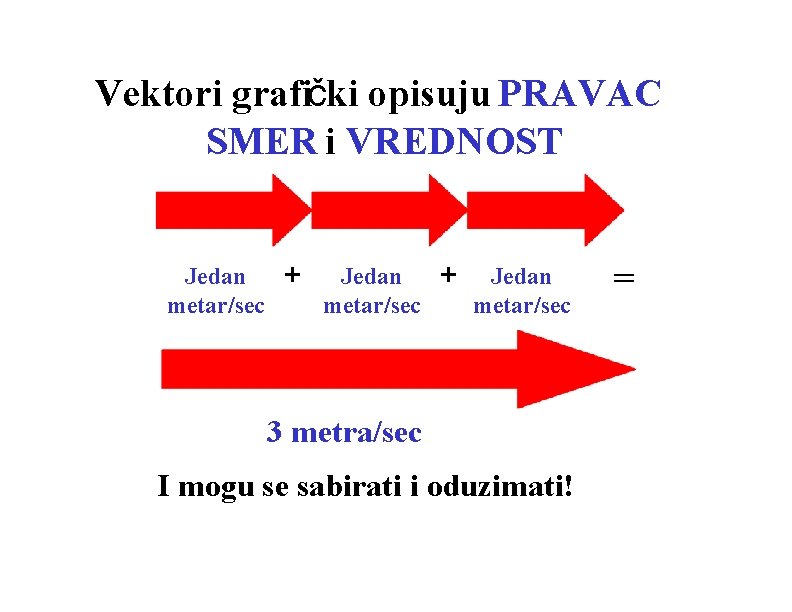
Vektori grafički opisuju PRAVAC SMER i VREDNOST Jedan metar/sec + Jedan metar/sec 3 metra/sec I mogu se sabirati i oduzimati! =

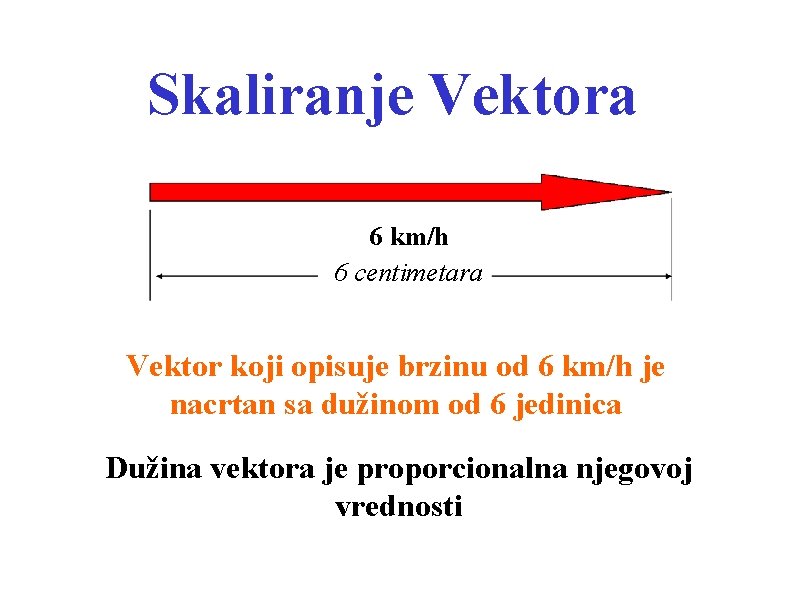
Skaliranje Vektora 6 km/h 6 centimetara Vektor koji opisuje brzinu od 6 km/h je nacrtan sa dužinom od 6 jedinica Dužina vektora je proporcionalna njegovoj vrednosti

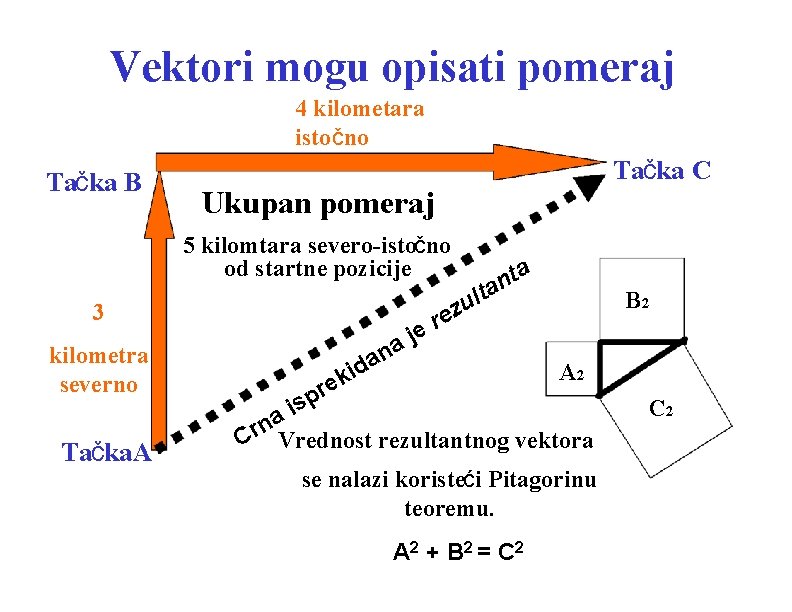
Vektori mogu opisati pomeraj 4 kilometara istočno Tačka B Tačka C Ukupan pomeraj 5 kilomtara severo-istočno od startne pozicije 3 kilometra severno Tačka. A e j a n ul z re ta n ta a d i k re B 2 A 2 sp i na r C Vrednost rezultantnog vektora se nalazi koristeći Pitagorinu teoremu. A 2 + B 2 = C 2

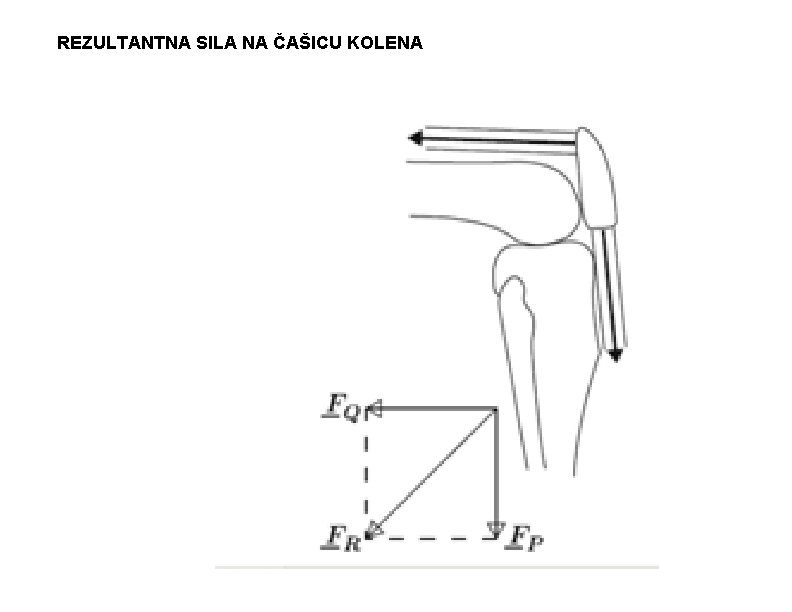
REZULTANTNA SILA NA ČAŠICU KOLENA

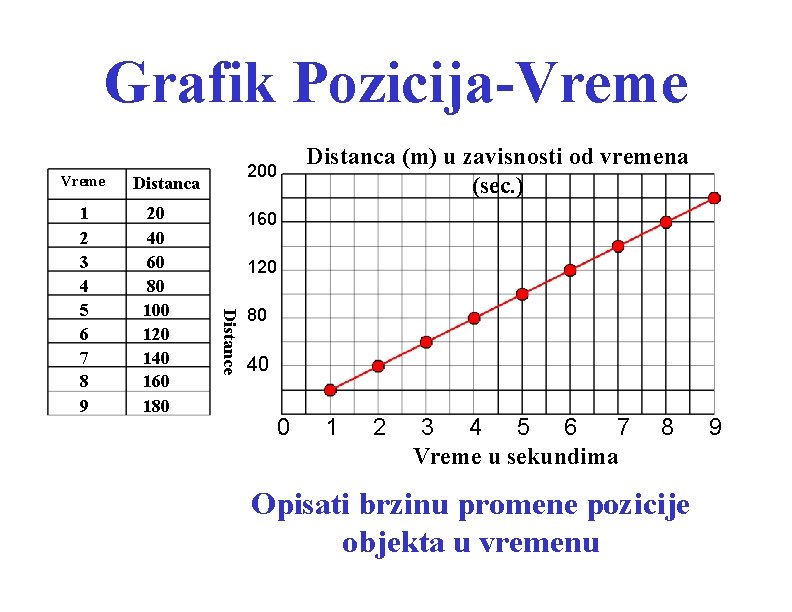
Grafik Pozicija-Vreme Distanca 20 40 60 80 100 120 140 160 180 Distanca (m) u zavisnosti od vremena (sec. ) 160 120 Distance 1 2 3 4 5 6 7 8 9 200 80 40 0 1 2 3 4 5 6 7 Vreme u sekundima 8 Opisati brzinu promene pozicije objekta u vremenu 9

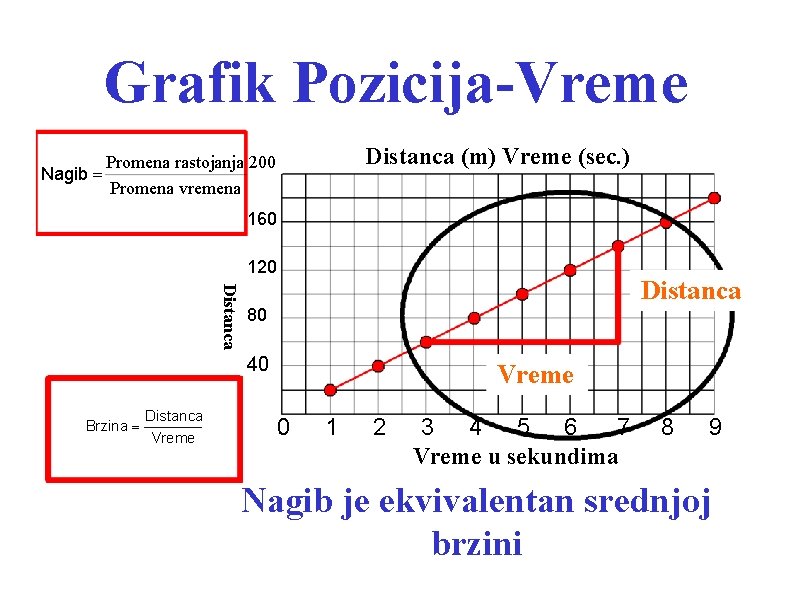
Grafik Pozicija-Vreme Nagib = Distanca (m) Vreme (sec. ) Promena rastojanja 200 Promena vremena 160 120 Distanca 80 40 Brzina = Distanca Vreme 0 1 2 3 4 5 6 7 Vreme u sekundima 8 9 Nagib je ekvivalentan srednjoj brzini

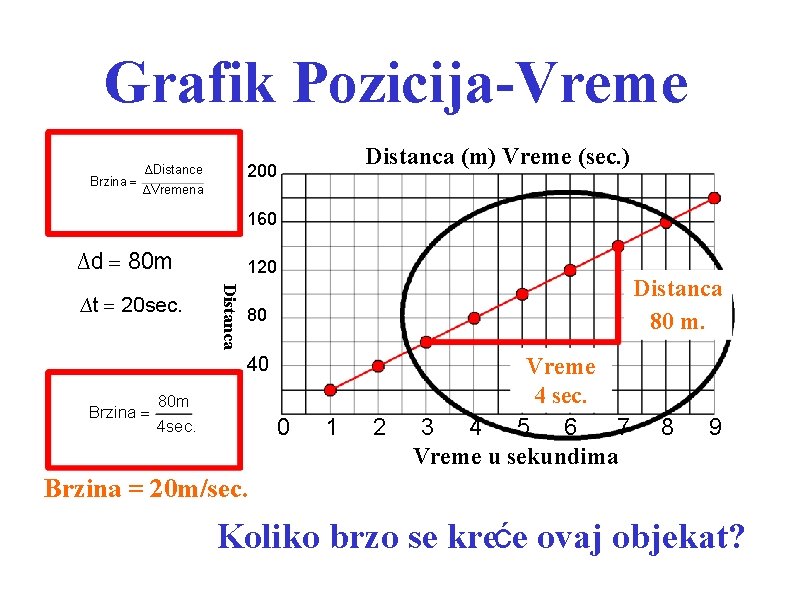
Grafik Pozicija-Vreme Brzina = Distanca (m) Vreme (sec. ) 200 ∆Distance ∆Vremena 160 ∆d = 80 m Distanca ∆t = 20 sec. 120 Distanca 80 m. 80 40 Brzina = 80 m 4 sec. 0 1 2 Vreme 4 sec. 3 4 5 6 7 Vreme u sekundima 8 9 Brzina = 20 m/sec. Koliko brzo se kreće ovaj objekat?

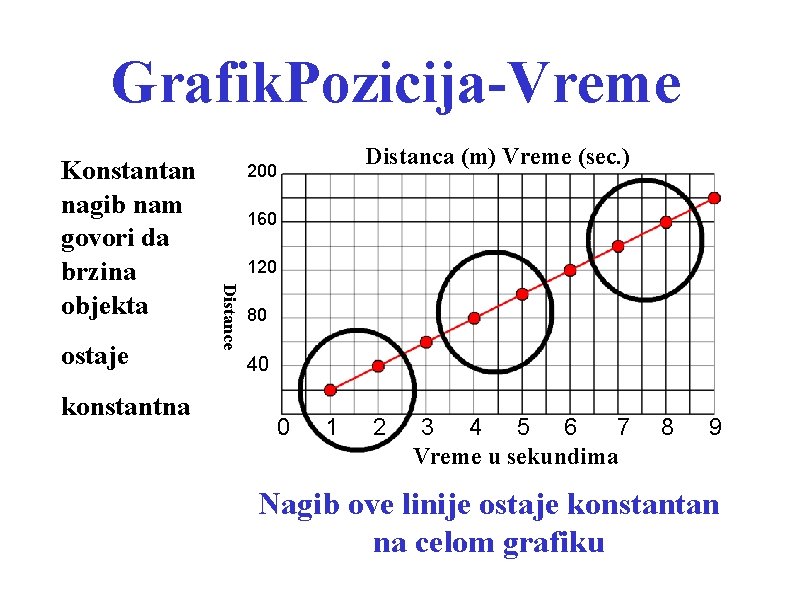
Grafik. Pozicija-Vreme ostaje konstantna Distanca (m) Vreme (sec. ) 200 160 120 Distance Konstantan nagib nam govori da brzina objekta 80 40 0 1 2 3 4 5 6 7 Vreme u sekundima 8 9 Nagib ove linije ostaje konstantan na celom grafiku

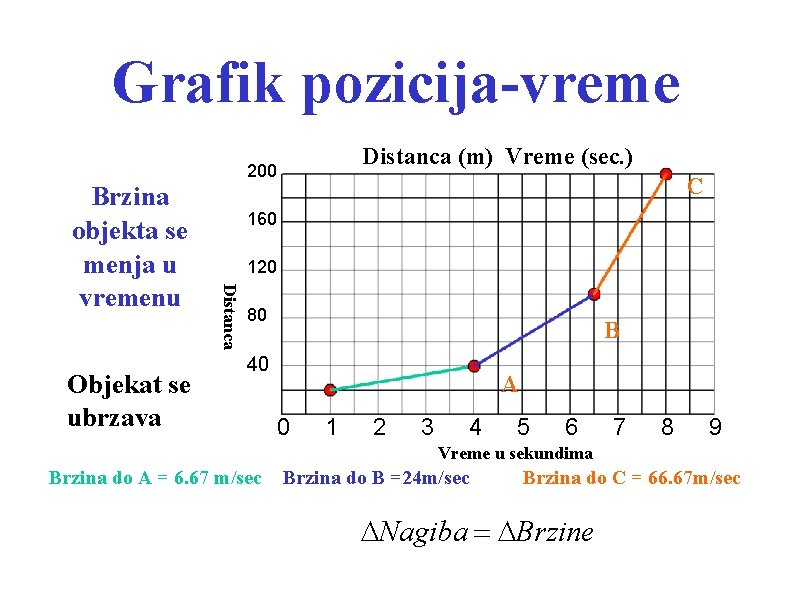
Grafik pozicija-vreme Distanca (m) Vreme (sec. ) 200 Objekat se ubrzava C 160 120 Distanca Brzina objekta se menja u vremenu 80 B 40 A 0 1 2 3 4 5 6 7 8 9 Vreme u sekundima Brzina do A = 6. 67 m/sec Brzina do B =24 m/sec Brzina do C = 66. 67 m/sec Nagiba = Brzine

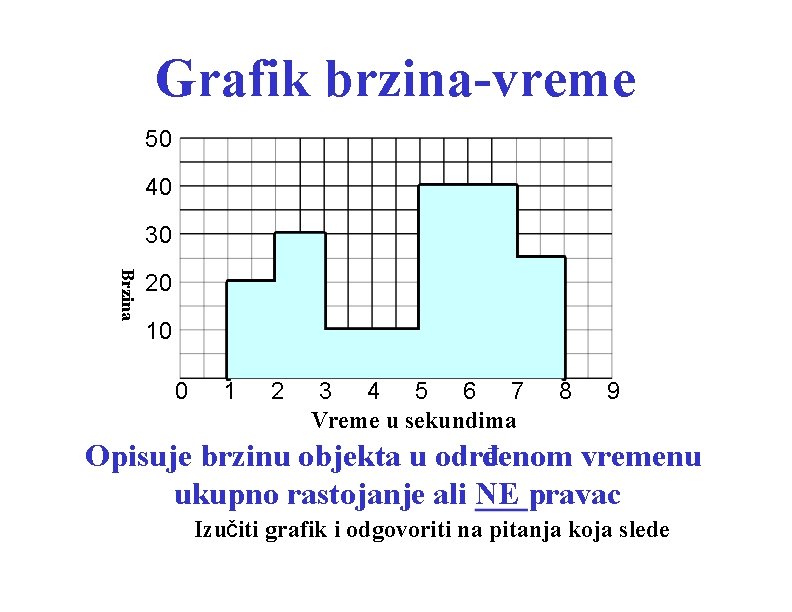
Grafik brzina-vreme 50 40 30 Brzina 20 10 0 1 2 3 4 5 6 7 Vreme u sekundima 8 9 Opisuje brzinu objekta u određenom vremenu ukupno rastojanje ali NE pravac Izučiti grafik i odgovoriti na pitanja koja slede

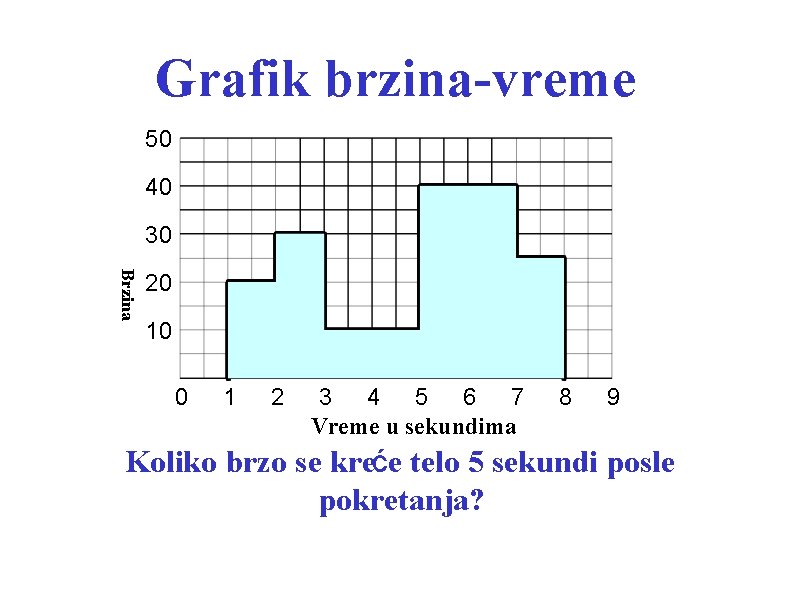
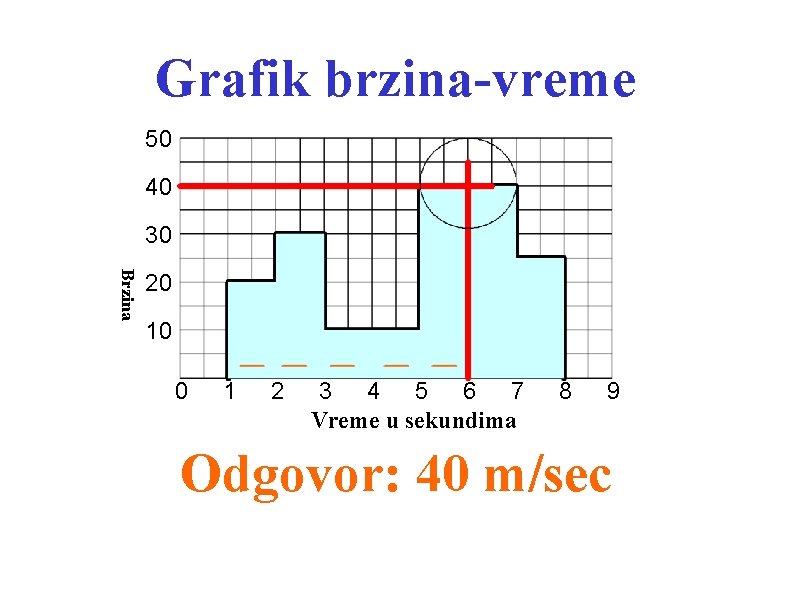
Grafik brzina-vreme 50 40 30 Brzina 20 10 0 1 2 3 4 5 6 7 Vreme u sekundima 8 9 Koliko brzo se kreće telo 5 sekundi posle pokretanja?

Grafik brzina-vreme 50 40 30 Brzina 20 10 0 1 2 3 4 5 6 7 Vreme u sekundima 8 9 Odgovor: 40 m/sec

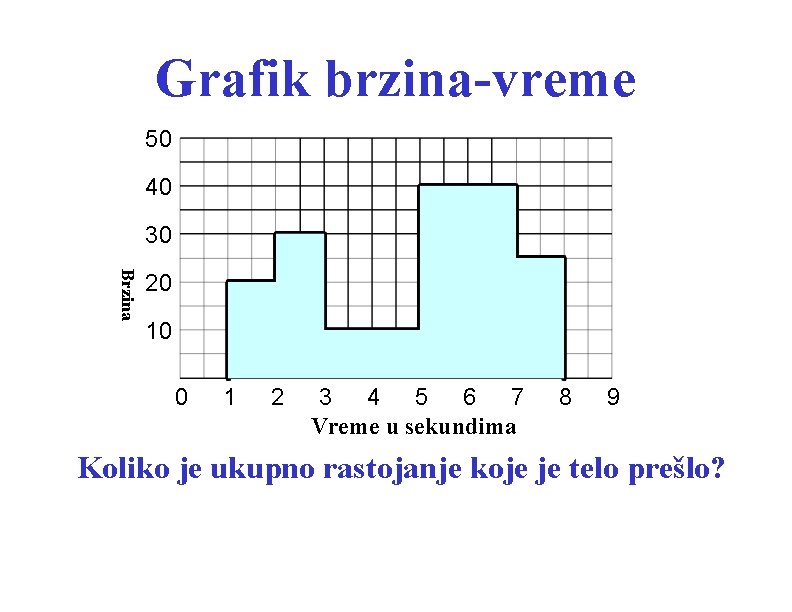
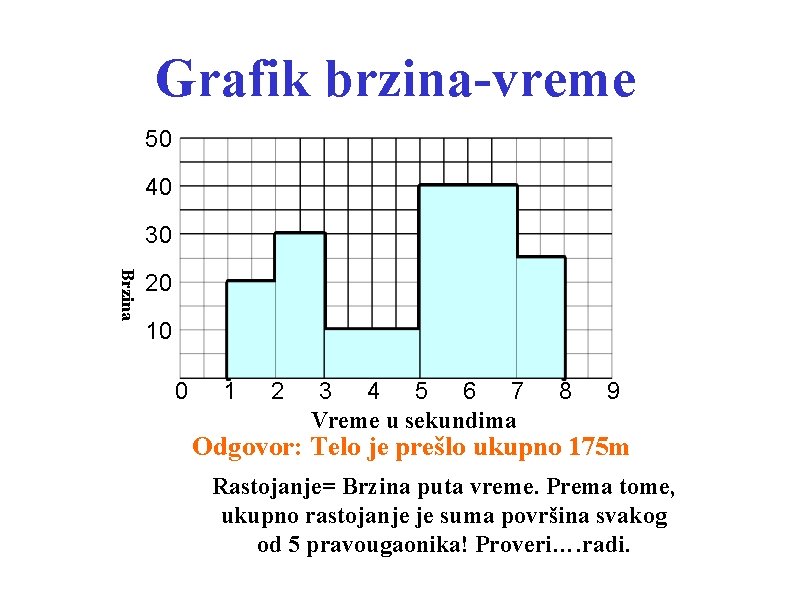
Grafik brzina-vreme 50 40 30 Brzina 20 10 0 1 2 3 4 5 6 7 Vreme u sekundima 8 9 Koliko je ukupno rastojanje koje je telo prešlo?

Grafik brzina-vreme 50 40 30 Brzina 20 10 0 1 2 3 4 5 6 7 Vreme u sekundima 8 9 Odgovor: Telo je prešlo ukupno 175 m Rastojanje= Brzina puta vreme. Prema tome, ukupno rastojanje je suma površina svakog od 5 pravougaonika! Proveri…. radi.