Fizikai kmia 2 Reakcikinetika Szmolsi gyakorlat Szmolsi gyakorlat

Fizikai kémia 2 – Reakciókinetika Számolási gyakorlat

Számolási gyakorlat • Házi feladatok, vetített diasorok, házi feladatok és zárthelyik eredményei: – samuviktor. web. elte. hu/Reakciokinetika_16_17_1 • Házi feladatok: – összesen kb. 10 -12 feladat, beadható papír alapon, illetve e-mail formájában (rkinhazi@gmail. com) is – beküldési határidő a feladatnál jelzett péntek 10: 00! • Konzultáció: – lesz kitűzött időpont – samuviktor@caesar. elte. hu

Ütközési elmélet, átmenetiállapot-elmélet 1. gyakorlat

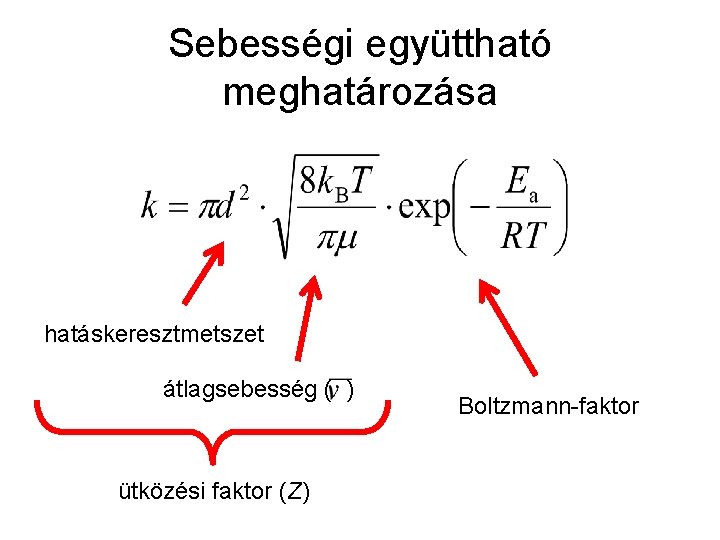
Ütközési elmélet • Feltétel: merev gömbök ütközése • Sebességi együttható számítása: • • • k: sebességi együttható d: gömbszerű részecskék (A és B) sugarának összege T: hőmérséklet μ: redukált tömeg Ea: aktiválási energia

Sebességi együttható meghatározása hatáskeresztmetszet átlagsebesség ( ) ütközési faktor (Z) Boltzmann-faktor

Ütközések száma • Az ütközések száma: • NA: az A részecskék száma egységnyi térfogatban

Ütközési elmélet • 1. feladat: a) Számítsuk ki az A és B molekulák közötti ütközések számát, ha mind az A, mind a B molekula parciális nyomása 100 torr 300 K hőmérsékleten, az A molekula átmérője 0, 3 nm, a B molekuláé 0, 4 nm, a részecskék átlagos sebessége pedig 5∙ 102 m/s ezen a hőmérsékleten. b) A ütközések hányad része történik elegendő energiával ahhoz, hogy végbemenjen a reakció az adott hőmérsékleten, ha az aktiválási energia 40 k. J/mol? c) Határozzuk meg a reakció sebességi együtthatóját!

Ütközési elmélet • 1. feladat: a) Számítsuk ki A és B molekula között az ütközések számát, ha mind az A, mind a B parciális nyomása 100 torr 300 K hőmérsékleten, az A molekula átmérője 0, 3 nm, B molekuláé 0, 4 nm, a részecskék átlagos sebessége pedig 5∙ 102 m/s ezen a hőmérsékleten.

Ütközési elmélet • 1. feladat: a)

Ütközési elmélet • 1. feladat: b) A ütközések hányad része történik elegendő energiával ahhoz, hogy végbemenjen a reakció az adott hőmérsékleten, ha az aktiválási energia 40 k. J/mol?

Ütközési elmélet • 1. feladat: c) Határozzuk meg a reakció sebességi együtthatóját!

Átmenetiállapot-elmélet (TST) • A termékek egy átmeneti állapoton keresztül keletkeznek – Unimolekulás reakció: A A termékek – Bimolekulás reakció: A + B AB termékek • Az egyensúlyi állandók kanonikus kifejezése: • : i-edik anyagfajta molekuláris állapotösszege standard állapotban • : i-edik anyagfajta sztöchiometriai száma • : reakció energiaváltozása 0 K-en

Egyensúlyi állandók meghatározása • Ideális gázokban a molekuláris állapotösszegek felbonthatóak négy komponensre: – transzlációs – forgási – rezgési – elektronikus

Transzlációs állapotösszeg • Dobozba zárt részecskének megszámolva az állapotait:

Forgási állapotösszeg • Lineáris molekula esetén: ahol B a forgási állandó • Egyéb esetben bonyolultabb formula:

Rezgési állapotösszeg • Harmonikus rezgés esetén: ahol ν a harmonikus rezgés frekvenciája • Több rezgés esetén a különböző rezgések állapotösszegeit össze kell szorozni a molekuláris rezgési állapotösszeg kifejezéséhez

Elektronikus állapotösszeg • Szobahőmérsékleten ritka, hogy elektronikusan gerjesztődjön egy molekula, de lehet degenerált az alapállapot: ahol ge a degenerációfok • Amennyiben van elérhető gerjesztett szint:

Sebességi együttható számítása átmenetiállapot-elmélet alapján • Sebességi együttható kanonikus sokaságon: – Unimolekulás reakcióra: reaktáns molekuláris állapotösszege standard állapot esetén – Bimolekulás reakcióra: átmeneti állapot standard molekuláris állapotösszege, a reakciókoordináta menti rezgés nélkül reaktáns(ok) és az átmeneti állapot közötti energiakülönbség 0 K-en

Átmenetiállapot-elmélet • 2. feladat: Határozzuk meg a reakció sebességi együtthatóját 300 K hőmérsékleten és 1 bar nyomáson, amennyiben ismert a I 2 -molekula rezgési frekvencia hullámszámban ( = 213, 54 cm− 1) és forgási állandója (B = 0, 0373 cm− 1), az átmeneti állapot forgási állandója (B = 0, 0364 cm− 1) és a reaktáns és az átmeneti állapot közötti energiakülönbség 0 K-en ( 205 k. J/mol).

Átmenetiállapot-elmélet • 2. feladat: Nem érdemes külön-külön kiszámolni az egyes állapotösszegeket, helyette számítsuk ki azok arányait! – transzlációs állapotösszeg: – forgási állapotösszeg:

Átmenetiállapot-elmélet • 2. feladat: – rezgési állapotösszeg: az átmeneti állapot elveszíti a reakciókoordináta menti rezgési szabadsági fokát, ezért lesz a számláló értéke 1 – elektronikus állapotösszeg:

Átmenetiállapot-elmélet • 2. feladat:

Köszönöm a figyelmet!