Fizika rettsgi felkszt MECHANIKA I Lszl Jzsef Bolyai

Fizika érettségi felkészítő MECHANIKA I. László József Bolyai Farkas Elméleti Líceum 2020

I. Kinematika

1. Az egyenesvonalú egyenletes mozgás • Jellemzése: • Az egyenesvonalú egyenletes mozgástörvénye: O xo(to) x(t) x , ha to = 0 s to – kezdeti pillanat; xo – kezdeti koordináta t – végső pillanat; x – végső koordináta vx – a sebességvektor vetülete az Ox tengelyre vx = +v, ha és vx = -v, ha x O O x

2. Az egyenesvonalú egyenletesen változó mozgás • Jellemzése: – a mozgás gyorsuló, ha a sebességvektor és a gyorsulásvektor irányítása megegyezik O x – a mozgás lassuló (fékezett), ha a sebességvektor és a gyorsulásvektor irányítása ellentétes O x

• Az egyenesvonalú egyenletesen változó mozgás törvényei: O O Legyen to = 0 s a) A mozgástörvény: b) A sebességtörvény: c) Galilei-képlete: xo(to) x(t) x x

3. Szabad mozgások nehézségi (gravitációs) térben 3. 1. A szabadesés y – nehézségi gyorsulás yo(to) • A szabadesés törvényei: y(t) Legyen to = 0 s a) Mozgástörvény: O b) Sebességtörvény: c) Galilei-képlete:

3. 2. A függőleges hajítás y y ymax yo y • A függőleges hajítás törvényei: yo Legyen to = 0 s y a) Mozgástörvény: b) Sebességtörvény: O O c) Galilei-képlete: lefele felfele

Feladatok 1. Egy vonat útjának felét 72 km/h sebességgel, a másik felét pedig 30 m/s sebességgel teszi meg. A vonat teljes útra számított átlagsebessége: a) 24 m/s b) 25 m/s c) 51 m/s d) 102 m/s Megoldás: O x d (t ) Algebrai megoldás Számérték:

2. Egy vonat a mozgásidő felét v 1 sebességgel, a másik felét pedig v 2 sebességgel teszi meg. A vonat teljes útra számított átlagsebessége: a) Megoldás: b) c) d) O x d (t ) Algebrai megoldás

v(m/s) 3. A mellékelt ábrán egy mozgó test sebességének idő szerinti változását ábrázoltuk. Az átlagsebesség értéke a mozgás egészére számítva: 8 5 t(s) 4 a) 3, 25 m/s b) 6, 50 m/s c) 7, 50 m/s 8 d) 13, 50 m/s Megoldás: A két mozgási szakaszban a test egyenesvonalú egyenletes mozgást végez , illetve sebességgel. A grafikonon megfigyelhető, hogy a két szakasz időtartama megegyezik: . A helyes megoldás megfelel az előző feladat megoldásának: Más megoldás: Számítsuk a grafikon alatti területet és osszuk el a teljes időtartammal. A grafikon alatti terület egyenlő a teljes úttal: Tehát:

4. Egy mozgó test sebességének idő szerinti változását a mellékelt grafikon ábrázolja. A 0 és 2 t 0 időpillanatok között a test által megtett távolság: a) 2 v 0 t 0 b) v 0 t 0 c) v 0 t 0/2 Megoldás: A grafikon értelmezése: Az előző feladat második (területes) megoldása alapján: d) v 0 t 0/4 vx v 0 t 0 2 t 0

II. Dinamika

1. Newton törvényei 1. 1. Newton első törvénye (A tehetetlenség elve) • Egy test megtartja egyenesvonalú egyenletes mozgását, vagy megmarad viszonylagos nyugalmi állapotában mindaddig, amíg a környezet nem hat rá, vagy a környezet összhatása nulla. – A testek tehetetlenek, a tehetetlenség mértéke a tömeg (m). A tömeg mértékegyesége:

1. 2. Newton második törvénye (A dinamika alapelve) – A testek közti kölcsönhatás mértéke az erő – Az eredő erő a testre ható erőrendszer vektoriális összege • Egy test gyorsulása egyenesen arányos a testre ható eredő erővel és fordítottan arányos a test tömegével. Az erő mértékegyesége:

A dinamika alaptörvényének másik megfogalmazása – Egy test mozgásállapotának mértéke az impulzus (lendület). Értelmezés szerint: – Az impulzus mértékegysége: – Ha egy test mozgásállapota stabil (transzlációs egyensúly), impulzusvektora állandó, egyenes vonalú egyenletes mozgást végez, vagy nyugalomban van. – A testre ható eredő erő megváltoztatja a test mozgásállapotát, impulzusváltozást okoz. • Egy testre ható eredő erő egyenlő a test impulzusváltozásának sebességével.

1. 2. Newton harmadik törvénye (A hatás-visszahatás elve) • Ha egy test hat egy másikra egy erővel, az utóbbi visszahat az előzőre egy ugyanakkora moduluszú, azonos irányú, és ellentétes irányítású erővel.

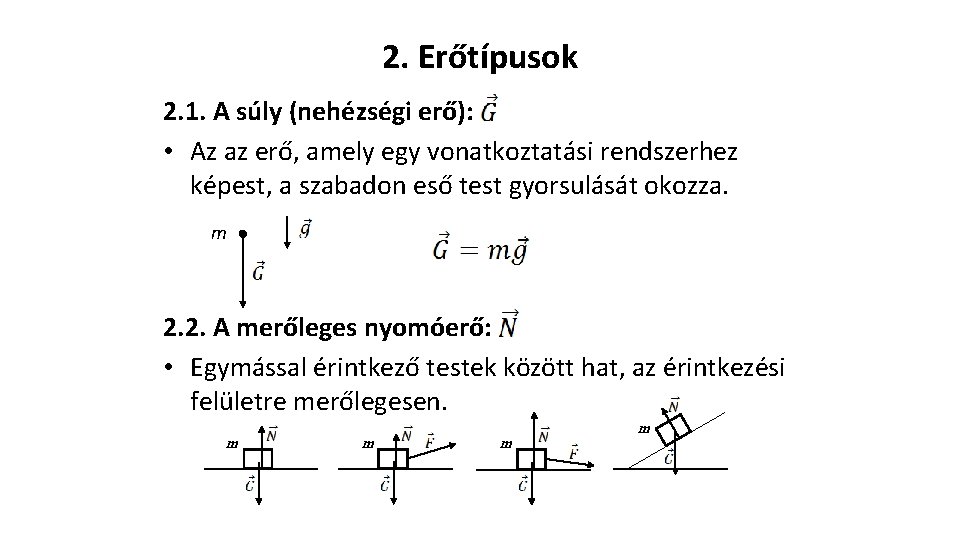
2. Erőtípusok 2. 1. A súly (nehézségi erő): • Az az erő, amely egy vonatkoztatási rendszerhez képest, a szabadon eső test gyorsulását okozza. m 2. 2. A merőleges nyomóerő: • Egymással érintkező testek között hat, az érintkezési felületre merőlegesen. m m

2. 3. A súrlódási erő: • Egymással érintkező testek között hat, az érintkezési felülethez viszonyítva érintőlegesen. Irányítása a tanulmányozott test viszonylagos elmozdulásával, vagy lehetséges elmozdulásával ellentétes. • Modulusza: , ahol a súrlódási együttható. A súrlódási erő modulusza nem függ az érintkezési felület nagyságától. • Okai: az érintkező felületek egyenetlenségei, valamint anyagaik molekuláris kölcsönhatása (tapadása). • Típusai: – sztatikus súrlódási erő; – kinetikus, vagy csúszási súrlódási erő.

• A súrlódási erő és a húzóerő viszonya: m m sztatikus kinetikus – nem függ a húzóerőtől • A csúszási (kinetikus) súrlódási együttható mérése tribométerrel. A súrlódási szög: tribométer = változtatható szögű lejtő m – súrlódási szög

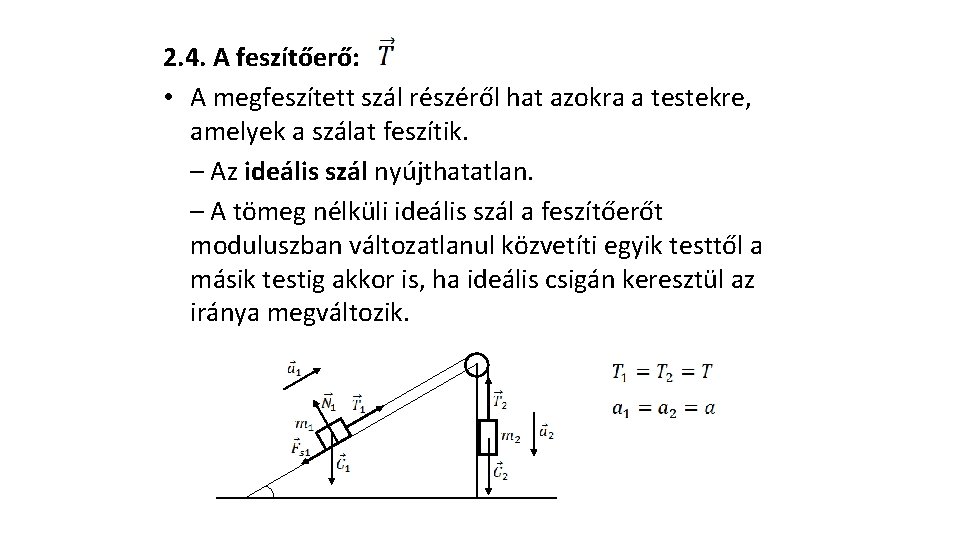
2. 4. A feszítőerő: • A megfeszített szál részéről hat azokra a testekre, amelyek a szálat feszítik. – Az ideális szál nyújthatatlan. – A tömeg nélküli ideális szál a feszítőerőt moduluszban változatlanul közvetíti egyik testtől a másik testig akkor is, ha ideális csigán keresztül az iránya megváltozik.

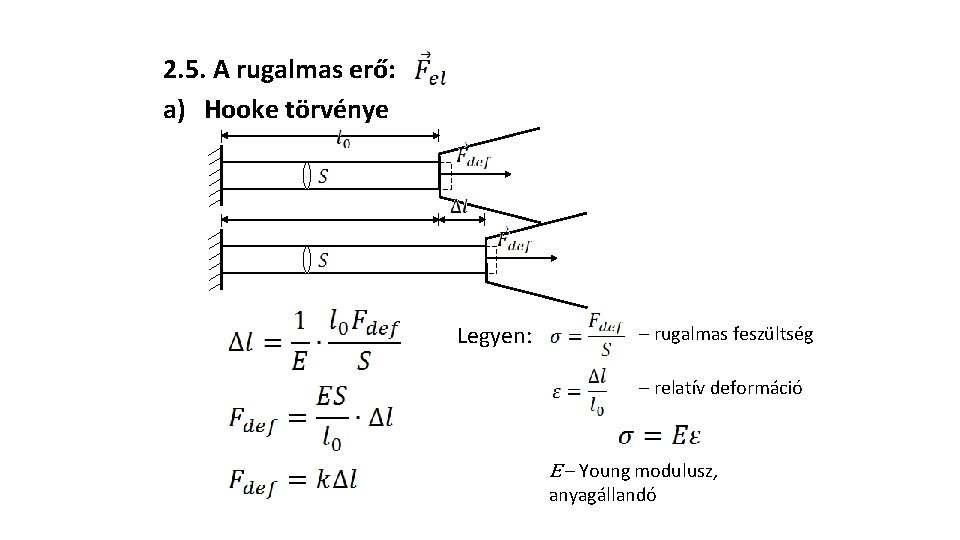
2. 5. A rugalmas erő: a) Hooke törvénye Legyen: – rugalmas feszültség – relatív deformáció E – Young modulusz, anyagállandó

b) A rugalmas erő: • Az az erő, amely a deformált rugó részéről hat azokra a testekre, amelyek a rugót deformálják. – Az ideális rugó tökéletesen rugalmas – A tömeg nélküli ideális rugó a rugalmas erőt moduluszban változatlanul közvetíti egyik testtől a másik testig. O x k – rugóállandó

Feladatok 1. Egy testre egy erő hat és a 1 gyorsulást okoz. Ugyanaz az erő egy másik test esetén a 2 gyorsulást eredményez. Ha ugyanazzal az erővel hatunk a két test összeragasztásával létrejött testre, az így okozott gyorsulás: a) b) c) d) Megoldás: Tehát:

2. Egy ember egy olyan liftben áll, amely a=2 m/s 2 függőlegesen lefele irányuló gyorsulással ereszkedik le. Az ember súlya és a lift padlójára általa gyakorolt nyomóerő aránya: a) 1 b) 1, 25 c) 1, 50 d) 1, 75 Megoldás: O Az ember gyorsulása megegyezik a lift gyorsulásával. A hatás- visszahatás elve alapján az ember által a liftre gyakorolt nyomóerő moduluszban egyenlő a lift által az emberre gyakorolt nyomóerővel (N). A dinamika alaptörvénye az emberre megfogalmazva az Oy tengely szerint: m y

3. Az m tömegű könyvet, a mellékelt ábra szerint az F erő segítségével, felefelé toljuk egy függőleges falon. Az erő a függőlegessel os szöget zár be. Tudva, hogy a könyv és a fal között a csúszási súrlódási együttható értéke , ahhoz, hogy a könyv állandó sebességgel mozogjon a falon fölfelé, az F erő értéke: a) Megoldás: b) c) y x d)

Köszönöm a figyelmet! Kérdéseket várunk a fizika. erettsegizoknek@gmail. com címre.