Fizika I Dr Gugolya Zoltn egyetemi docens Pannon

Fizika I. Dr. Gugolya Zoltán egyetemi docens Pannon Egyetem Fizika Intézet N. ép. II. em. 232. szoba E-mail: gug 006@almos. vein. hu Tel: 88/624 -783

Fizika I. Ajánlott irodalom: • Vonderviszt-Németh-Szalai: Fizika I. Veszprémi Egyetemi Kiadó 2003. • Budó Ágoston: Kísérleti fizika I. Tankönyvkiadó Budapest • Feynman: Mai fizika, Műszaki Könyvkiadó, Budapest • Középiskolás fizika tankönyvek

Fizika I. TÉTELSOR 1. 2. 3. 4. Koordinátarendszerek, helyvektor, út, elmozdulás, sebesség, gyorsulás. Egyenes vonalú mozgások, hajítás. Körmozgás, harmonikus rezgőmozgás. Dinamika, Newton törvényei. Tömeg, impulzus, erőtörvények. Mozgásegyenlet. 5. Kényszermozgások, lejtő, súrlódás. 6. A gravitáció. Bolygók mozgása, Kepler törvényei. Az általános tömegvonzás törvénye. 7. Munka, energia, teljesítmény. A kinetikus energia tétele. Konzervatív erőterek. A mechanikai energia megmaradása. 8. Harmonikus rezgőmozgás dinamikája 9. Pontrendszerek mechanikája, tömegközéppont és impulzustétel. 10. Ütközések. Impulzusmomentum, impulzusmomentum-tétel. 11. A merev test mechanikája. Tehetetlenségi nyomaték, a forgó mozgás alapegyenlete 12. Hullámok

Vizsgaidőpontok 2009. 12. 15. 9: 00 2009. 12. 17. 9: 00 2010. 01. 04. 9: 00 2010. 01. 06. 9: 00 2010. 01. 08. 9: 00 2010. 01. 12. 9: 00 2010. 01. 14. 9: 00 2010. 01. 18. 9: 00 2010. 01. 20. 9: 00 2010. 01. 21. 9: 00

A FIZIKA tárgya: - állandóan változik felosztása: mechanika, hangtan, hőtan, fénytan, elektromosság…. . (pl. régebben az érzékszervekre gyakorolt hatás alapján történt) A megfigyelések a tudatos kísérletezéseken keresztül olyan elméletek felállításához vezettek, amelyek a természeti jelenségeket ellentmondásmentesen írják le. Az elméletekben nagy mennyiségű kísérleti tapasztalat összegződik! Egy elmélet nem biztos, hogy egyetemes igazságot fejez ki, bármikor előkerülhet egy olyan kísérlet melynek eredménye ellentmond az elméletnek. Ilyenkor finomítani, módosítani kell az elméletet, vagy gyökeresen új elmélet kerül a régi helyére.

Mechanika Kinematika A kinematika feladata egy tömegpont, vagy részecske mozgásának leírása. A tömegpont (anyagi pont) olyan test, amelynek méretei a vizsgált esetben elhanyagolhatóak. • A kinematika a hol? és a mikor? kérdésekre keresi a választ. A fizikai jelenségek térben és időben játszódnak le. • A kinematika leírásokhoz a Newton féle tér és idő fogalmát használjuk, ami mindennapi tapasztalatainkból fokozatosan fejlődött ki.

• A teret – homogénnek (a tér tulajdonságai nem függnek a helytől) és – izotropnak tekintjük (a tér tulajdonságai nem függnek az iránytól). • Minden test a tér egy adott helyén tartózkodik, és az idő múlásával változtatja helyzetét. Egy kiválasztott test helyzetét a térben egy rögzített vonatkoztatási rendszerhez képest adhatjuk meg. • Az idő Newton szerint szintén abszolút, abban az értelemben, hogy egyenletesen telik.

A teret és az időt mérhetjük: Mérés: összehasonlítani egységgel • A hosszúság alapegysége a méter (m). A méter az a hosszúság, amelyet a vákuumban terjedő fény 1/299 792 458 másodperc alatt megtesz. • Az időtartam alapegysége a szekundum vagy másodperc(s). A másodperc definíció szerint a cézium 133 -as izotópjának két meghatározott energiaszintje közötti elektronátmenet során kibocsátott sugárzás periódusidejének 9 192 631 770 -szerese.

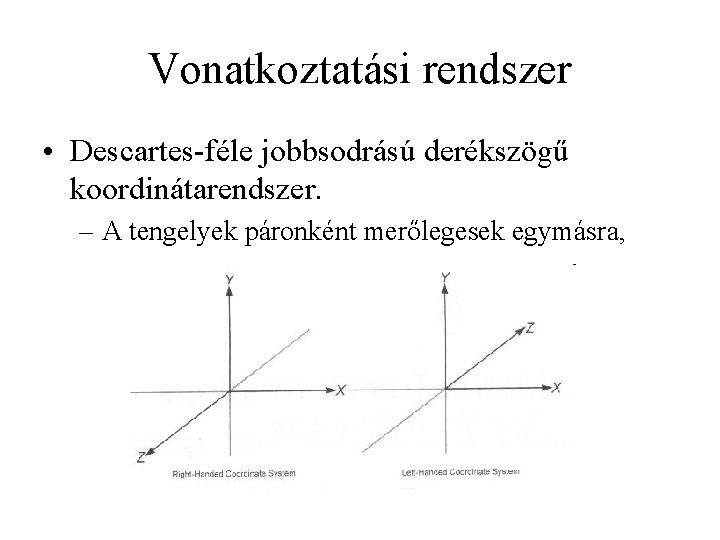
Vonatkoztatási rendszer • Descartes-féle jobbsodrású derékszögű koordinátarendszer. – A tengelyek páronként merőlegesek egymásra,

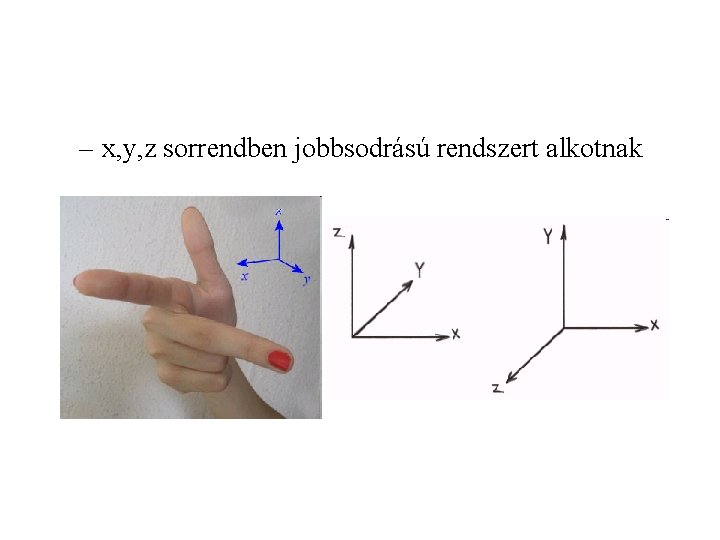
– x, y, z sorrendben jobbsodrású rendszert alkotnak

Tömegpont helyzete síkban A síkbeli Descartes-koordinátarendszerben egy P pont helyzetét az xy síkon az (x, y) koordinátakettőssel adhatjuk meg. A két tengely metszéspontja a koordinátarendszer kezdőpontja vagy origója. • x a P pont előjeles távolsága az y-tengelytől • y a P pont előjeles távolsága az x-tengelytől.

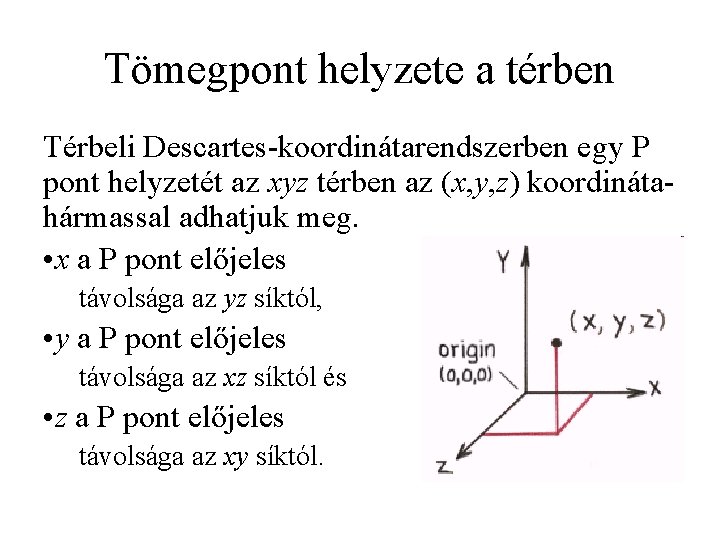
Tömegpont helyzete a térben Térbeli Descartes-koordinátarendszerben egy P pont helyzetét az xyz térben az (x, y, z) koordinátahármassal adhatjuk meg. • x a P pont előjeles távolsága az yz síktól, • y a P pont előjeles távolsága az xz síktól és • z a P pont előjeles távolsága az xy síktól.

Polár koordináták síkban • r a pontnak az origótól való távolsága • f az r és az x tengely által bezárt szög

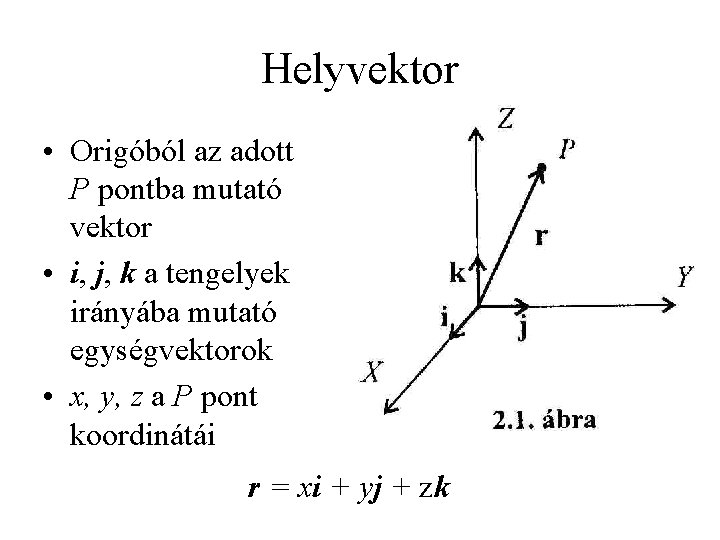
Helyvektor • Origóból az adott P pontba mutató vektor • i, j, k a tengelyek irányába mutató egységvektorok • x, y, z a P pont koordinátái r = xi + yj + zk

Pálya A tömegpont mozgását akkor tekintjük ismertnek, ha meg tudjuk adni a helyét bármely t időpillanatban, azaz ha ismerjük az r(t) függvényt: r(t) = x(t)i + y(t)j + z(t)k Ez egyértelműen meghatározza a tömegpont pályáját, azaz a mozgása során leírt térbeli görbét.

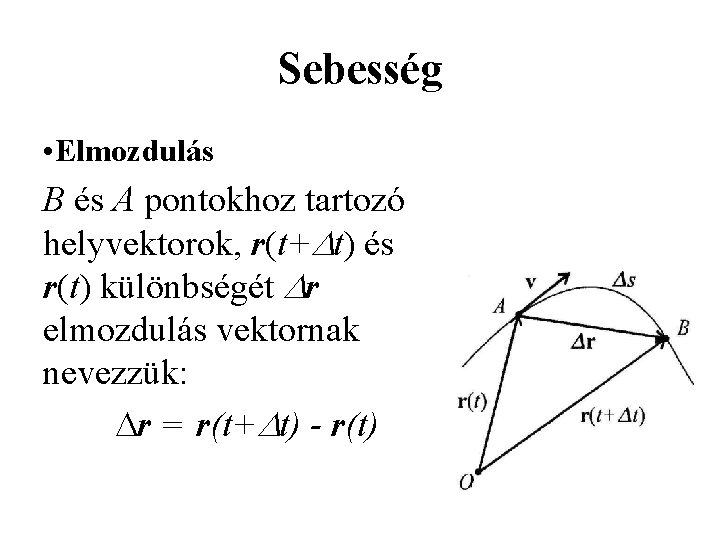
Sebesség • Elmozdulás B és A pontokhoz tartozó helyvektorok, r(t+ t) és r(t) különbségét r elmozdulás vektornak nevezzük: r = r(t+ t) - r(t)

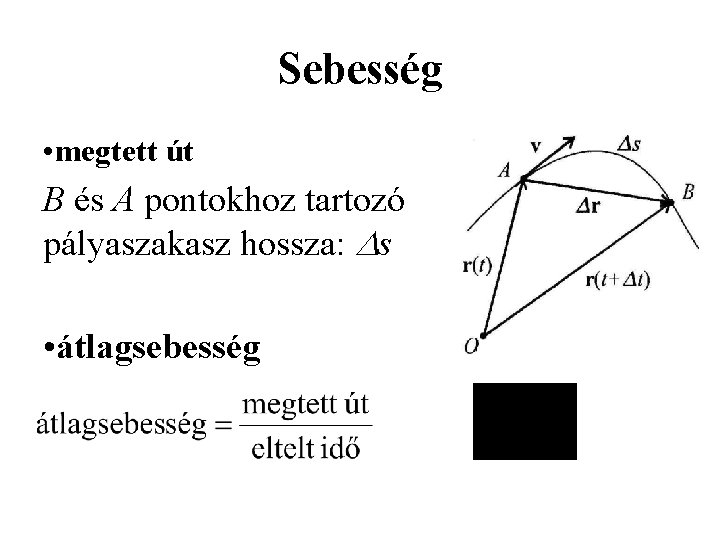
Sebesség • megtett út B és A pontokhoz tartozó pályaszakasz hossza: s • átlagsebesség

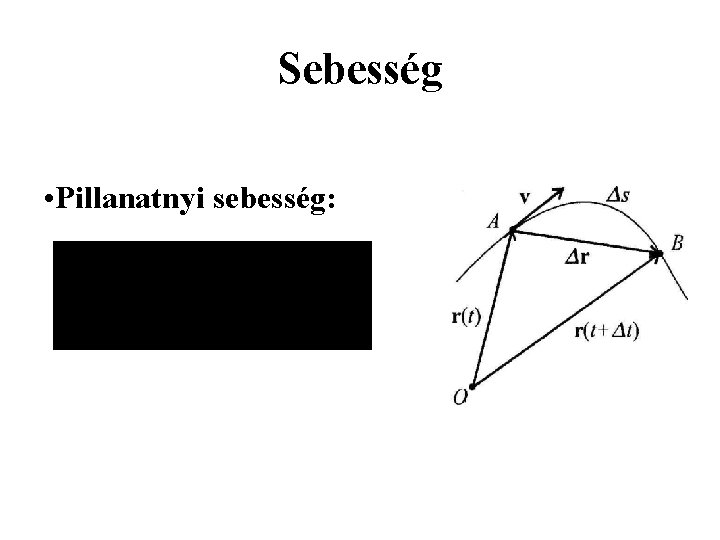
Sebesség • Pillanatnyi sebesség:

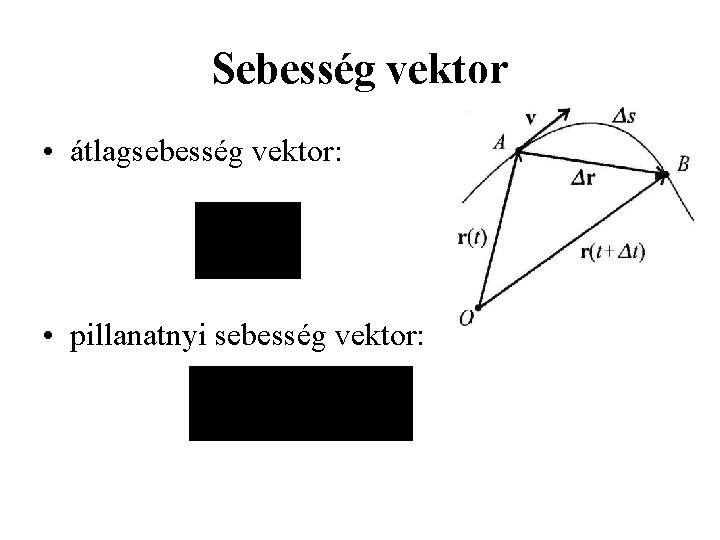
Sebesség vektor • átlagsebesség vektor: • pillanatnyi sebesség vektor:

Sebesség vektor • a sebesség vektor, a helyvektor idő szerinti (első) differenciálhányadosa • mértékegysége: m/s (km/h) • a sebességvektor mindig a pálya érintőjének irányába mutat.

Gyorsulás • A sebesség megváltozása: • A gyorsulás a sebesség idő szerinti első, vagy a helyvektor idő szerinti második differenciálhányadosa • mértékegysége: m/s 2

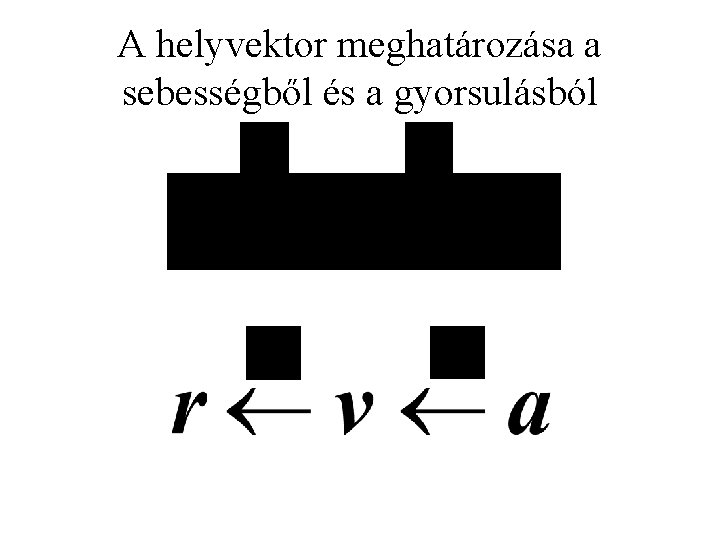
A helyvektor meghatározása a sebességből és a gyorsulásból

A helyvektor meghatározása a sebességből és a gyorsulásból v(t 0) a kezdőfeltétel r(t 0) a kezdőfeltétel

Speciális mozgások • • • Egyenes vonalú egyenletes mozgás Egyenes vonalú egyenletesen változó mozgás Ferde hajítás Körmozgás Harmonikus rezgőmozgás

Egyenes vonalú egyenletes mozgás A pálya egyenes. A mozgás egyenese legyen a koordináta rendszerünk x tengelye. Egyenes vonalú egyenletes a mozgás ha a gyorsulás=0 Þ sebesség = állandó v(t) = v 0 Þ x(t) = v 0 t + x 0

Egyenes vonalú egyenletesen változó mozgás egyenese legyen a koordináta rendszerünk x tengelye Egyenes vonalú egyenletesen változó a mozgás ha a gyorsulás = állandó (a 0 ) Þ v(t) = a 0 t + v 0 Þ x(t) = ½ a 0 t 2 + v 0 t + x 0

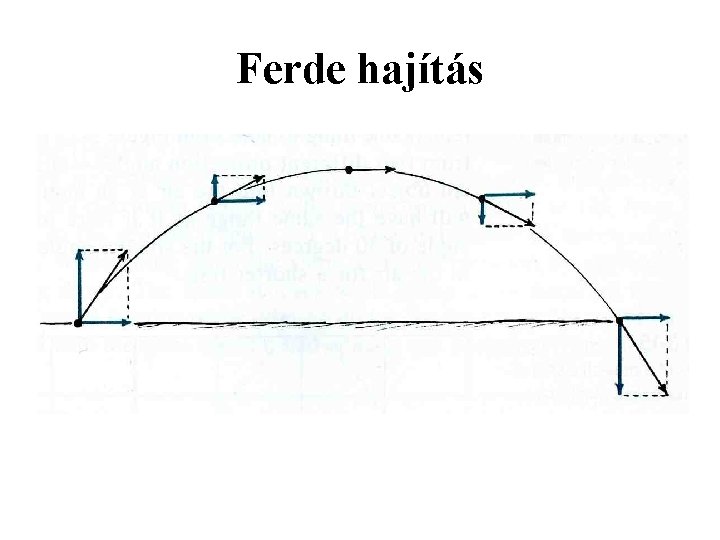
Ferde hajítás

Ferde hajítás • a gyorsulás komponensei: ax= 0 , ay = -g , az = 0 kezdeti feltételek t = 0 -nál: x= x 0 y= y 0 z= z 0 =0; v= v 0 • a sebesség komponensei: vx 0 = v 0 cos ; vy 0 = -gt+v 0 sin ; vz 0 = 0

Ferde hajítás • A helyvektor koordinátafüggvényei:

Ferde hajítás • Pályaegyenlet: parabola pálya • az emelkedés ideje: • a hajítás magassága:

Ferde hajítás • a hajítás távolsága vízszintes talajon:

Körmozgás • Egyenletes körmozgást végez a tömegpont akkor, ha egy körpályán egyenlő időközök alatt, egyenlő utakat tesz meg, mindig ugyanabban a körüljárási irányban. Þ a sebesség nagysága a mozgás során állandó, iránya NEM. szögsebesség:

Szögsebesség, szöggyorsulás Szögsebesség alatt a szögelfordulás idő szerinti differenciálhányadosát értjük: [1/s] A szöggyorsulás a szögsebesség idő szerinti differenciálhányadosa: [1/s 2]

Körmozgás A forgásszög ívmértéke és a kerületen megtett út közti összefüggés: A kerületi sebesség és a kerületi (tangenciális) gyorsulás innen: és a gyorsulás normális komp. :

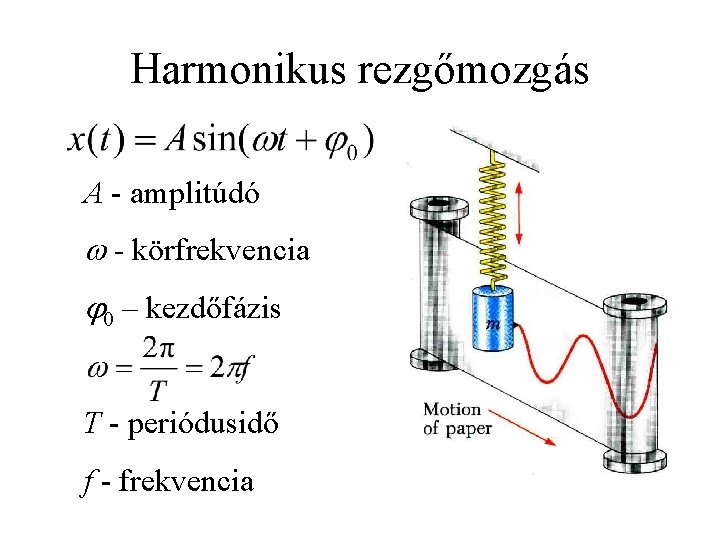
Harmonikus rezgőmozgás A - amplitúdó - körfrekvencia 0 – kezdőfázis T - periódusidő f - frekvencia

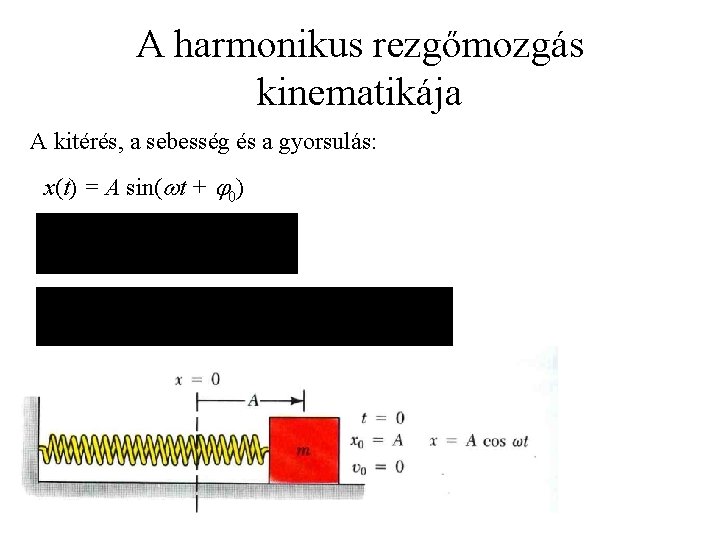
A harmonikus rezgőmozgás kinematikája A kitérés, a sebesség és a gyorsulás: x(t) = A sin( t + 0)

A DINAMIKA ALAPTÖRVÉNYEI Az axiómák közvetlenül nem bizonyítható tételek, noha nyilvánvalóan a bennük megfogalmazott állítások eredendően a tapasztalatban gyökereznek. Igazságukat a belőlük levonható következtetések tapasztalattal való egyezése dönti el. A tapasztalat pedig azt mutatja, hogy a Newton-féle dinamika alapján precízen leírható a mechanikai jelenségek rendkívül széles köre. De mint minden fizikai elméletnek, a newtoni dinamikának is megvannak a maga korlátai: nagyon gyors, a fénysebességet megközelítő mozgások esetén, valamint a mikrorészecskék világában a klasszikus elmélet kiegészítésre szorul.

A dinamika alaptörvényei Elsősorban Galilei korábbi eredményeire alapozva Newton foglalta rendszerbe a dinamika alaptörvényeit, amelyeket Newton axiómáknak nevezünk: Newton I. axiómája Minden test megmarad a nyugalom vagy az egyenes vonalú egyenletes mozgás állapotában, míg más testek hatásai állapotának megváltoztatására nem kényszerítik. (A tehetetlenség „törvénye”) Inerciarendszerben igaz!

A dinamika alaptörvényei • Bizonyos vonatkoztatási rendszerekben a tehetetlenség törvénye nem érvényes. • Newton I. axiómája burkoltan magában foglalja azt az állítást, hogy léteznek olyan vonatkoztatási rendszerek, amelyekben a tehetetlenség törvénye teljesül. Ezeket inerciarendszereknek nevezzük. • Inerciarendszer: idealizáció, ellenőrzés tapasztalatokkal

A dinamika alaptörvényei Newton II. axiómája Egy testre ható eredő erő a test tömegének és gyorsulásának szorzatával egyenlő. (A dinamika alaptörvénye) F=ma m: a tömeg, a testek tehetetlenségének mértéke.

Tömeg Egy ismeretlen test m tömegének meghatározása: alkalmazzunk azonos F erőt az m 0 és m tömegekre és mérjük meg, hogy azok mekkora a 0 illetve a gyorsulásra tesznek szert. F = ma F = m 0 a 0 és Az erők egyenlősége miatt: m 0 a 0 = m a azaz F = m a

Impulzus Az impulzus (lendület, mozgásmennyiség): I = mv [kgm/s] Az erő az impulzusváltozás gyorsasága: (ha m állandó)

A dinamika alaptörvényei Newton III. axiómája Ha egy A testre a B test FAB erőt gyakorol, akkor az A test is hat B-re ugyanolyan nagyságú, de ellentétes irányú erővel. (A hatás-ellenhatás törvénye) FAB = - FBA

A dinamika alaptörvényei Newton III. axiómája Ha az anyagi pontra egyidejűleg több erő hat (F 1, F 2, …), akkor ezek együttes hatása egyenértékű vektori eredőjük hatásával. (Az erőhatások függetlenségének elve)

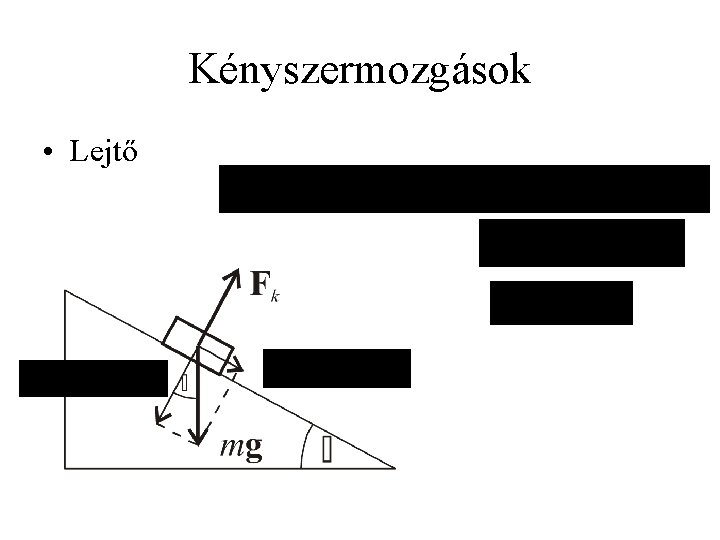
Kényszermozgások Kényszermozgás során a test mozgását valamilyen geometriai feltételek korlátozzák, ami általában abban nyilvánul meg, hogy a mozgás folyamán a testnek egy meghatározott felületen vagy görbén kell maradnia. Az erőt, amely a kényszert biztosítja (pl. adott felületen tartja a testet) kényszererőnek, a geometriai feltételt pedig kényszernek, vagy kényszerfeltételnek nevezzük. A kényszererő iránya merőleges a kényszerfelületre. Ha egy erőről hangsúlyozni akarjuk, hogy nem kényszererő, szabaderőnek nevezzük.

Kényszermozgások • Lejtő

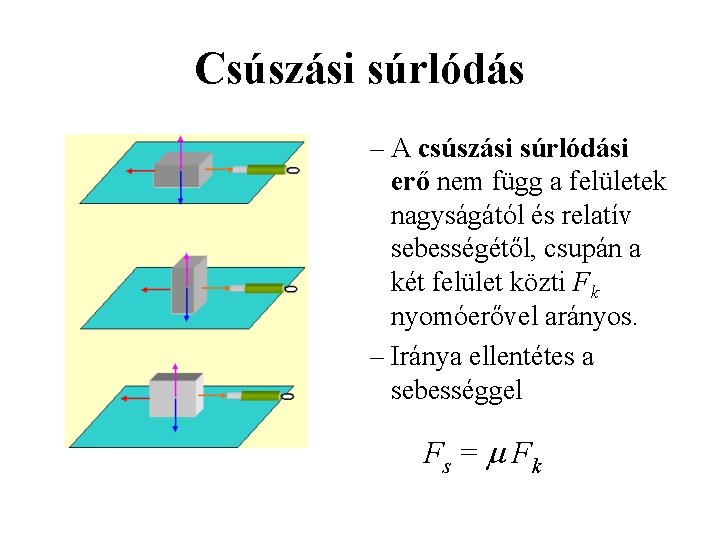
Súrlódás • Mozgást akadályozó erők Ha vízszintes felületen húzunk egy ládát, akkor is erőt kell kifejtenünk. Ha ellökünk egy testet, akkor csúszás közben csökken a sebessége. Tehát a csúszó testekre hat egy fékezőerő.

Csúszási súrlódás – A csúszási súrlódási erő nem függ a felületek nagyságától és relatív sebességétől, csupán a két felület közti Fk nyomóerővel arányos. – Iránya ellentétes a sebességgel Fs = Fk

Tapadási súrlódás • Tapadási súrlódásról akkor beszélünk, ha a testek egymáshoz képest nem mozognak. • Tapasztalat: Ha például egy szekrényt odébb akarok tolni, akkor egy bizonyos nagyságú erőnél nagyobbat kell kifejtenem, különben a szekrény nem mozdul el. Ha a szekrény nem mozdul el, akkor a ráható erők eredője 0. A talajnak olyan erőt kell kifejtenie, amely az általam kifejtett erőt ellensúlyozza, vagyis a talaj vízszintesen ugyanakkora csak ellentétes irányú erővel nyomja a szekrényt, mint én.

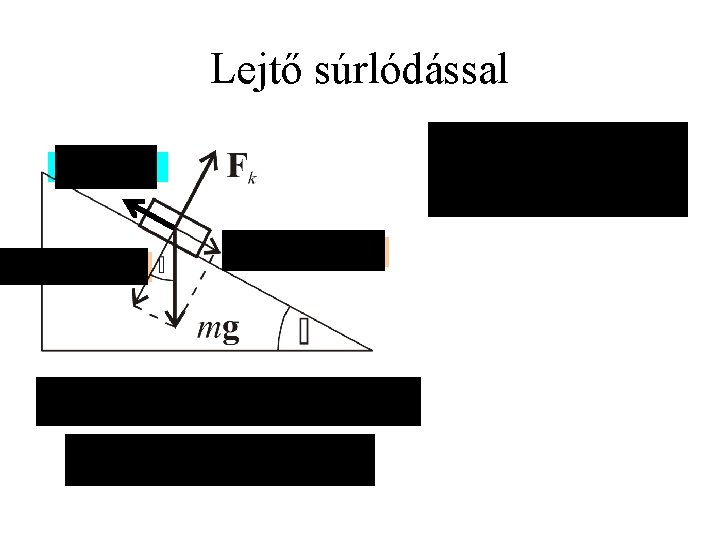
Tapadási súrlódási erő • A vizsgálatok szerint a tapadási súrlódási erő maximális értéke arányos az érintkező felületek között merőlegesen ható nyomóerővel, függ érintkező felületek anyagi minőségtől, de nem függ az érintkező felületek nagyságától: • A tapadási súrlódási együttható mindig nagyobb mint a csúszási súrlódási együttható:

Lejtő súrlódással

A bolygók mozgása A Naprendszerhez tartozó bolygók a Naptól kifelé haladva: Merkúr, Vénusz, Föld, Mars, Jupiter, Szaturnusz, Uránusz, Neptunusz, (a Plútó már csak törpebolygó).

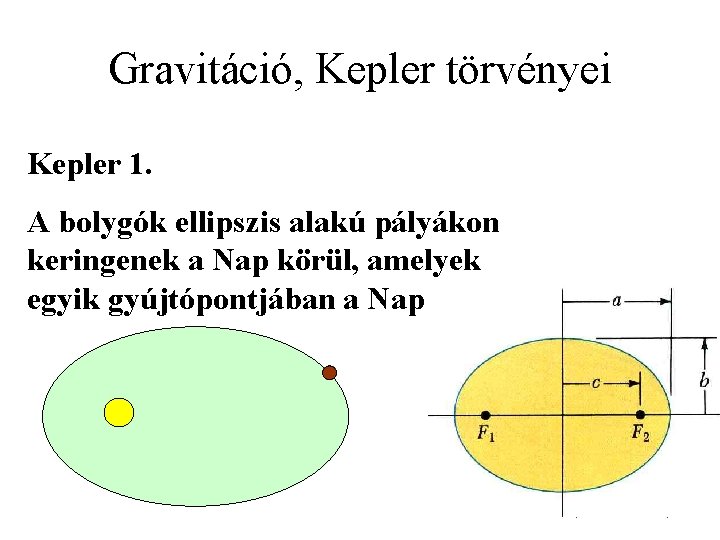
Gravitáció, Kepler törvényei Kepler 1. A bolygók ellipszis alakú pályákon keringenek a Nap körül, amelyek egyik gyújtópontjában a Nap áll. Johannes Kepler (1571 – 1630)

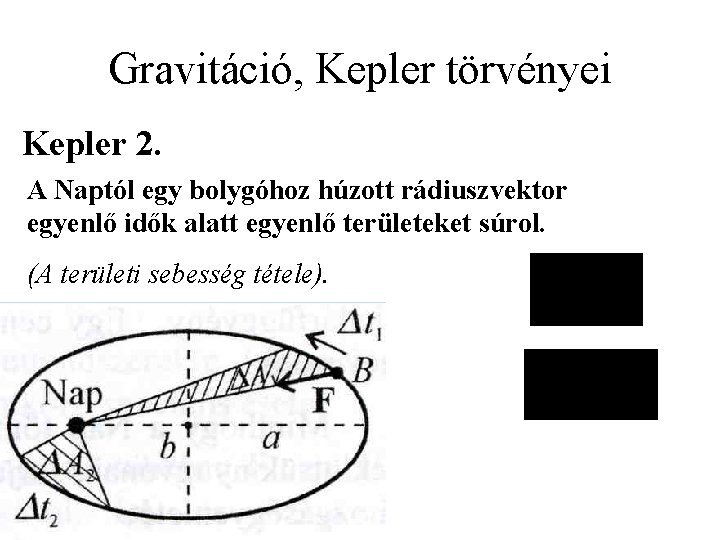
Gravitáció, Kepler törvényei Kepler 2. A Naptól egy bolygóhoz húzott rádiuszvektor egyenlő idők alatt egyenlő területeket súrol. (A területi sebesség tétele).

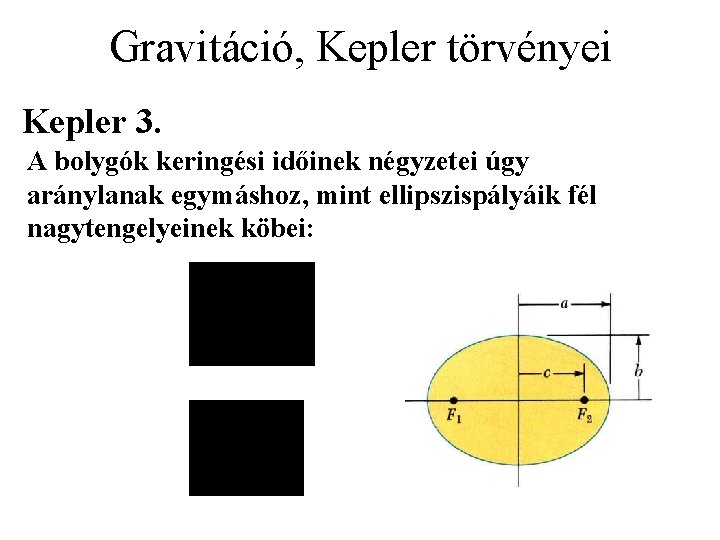
Gravitáció, Kepler törvényei Kepler 3. A bolygók keringési időinek négyzetei úgy aránylanak egymáshoz, mint ellipszispályáik fél nagytengelyeinek köbei:

A bolygók mozgása Kepler III. törvényét felhasználva meghatározhatjuk a Nap által kifejtett erő távolságfüggését. Az egyszerűség kedvéért tekintsünk egy olyan bolygót, pl. a Földet, amelyre az ellipszis pálya jó közelítéssel körnek tekinthető. A Nap által a Földre kifejtett FNF vonzóerő biztosítja az r sugarú egyenletes körmozgáshoz szükséges centripetális erőt:

A bolygók mozgása a Kepler III. alapján: ahol CN minden bolygóra ugyanaz, csak a Nap tulajdonságaitól függő mennyiség A Nap által a Földre kifejtett erő:

A bolygók mozgása Newton. III. tv. szerint, a Föld is ugyanilyen nagyságú, de ellentétes irányú erővel hat a Napra. Ha a Nap által kifejtett erő arányos a Föld tömegével, akkor a szimmetria miatt a Föld által a Napra kifejtett erőnek is arányosnak kell lennie a Nap tömegével (m. N), azaz: ahol sem a bolygó, sem a Nap tömegét nem tartalmazó univerzális állandó.

A bolygók mozgása Így: Általánosan elmondhatjuk, hogy a Nap az egyes bolygókra vonzóerőt fejt ki, amely arányos mind a Nap, mind az adott bolygó tömegével, s fordítottan arányos távolságuk négyzetével:

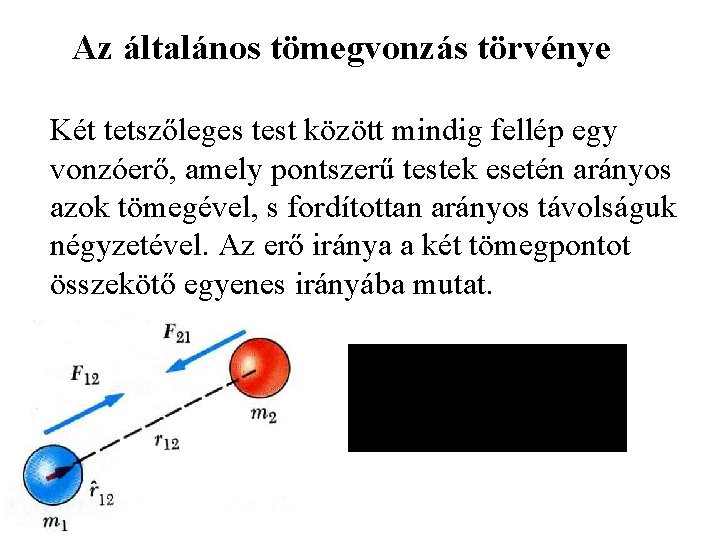
Az általános tömegvonzás törvénye Két tetszőleges test között mindig fellép egy vonzóerő, amely pontszerű testek esetén arányos azok tömegével, s fordítottan arányos távolságuk négyzetével. Az erő iránya a két tömegpontot összekötő egyenes irányába mutat.

Nehézségi gyorsulás A különböző testek anyagi minőségüktől függetlenül azonos g gyorsulással esnek a Föld felé, amelyet nehézségi gyorsulásnak nevezünk. Tekintsünk egy a Föld tömegvonzásának hatására a felszín felett h magasságban g gyorsulással szabadon eső m tömegű testet. A dinamika alapegyenlete szerint: A Föld felszínén h=0, ebből a g:

A tehetetlen és a súlyos tömeg tehetetlen súlyos tömeg („gravitációs töltés”) Tekintsünk két testet, amelyek súlyos és tehetetlen tömegét jelölje ms 1, ms 2 illetve mt 1, mt 2. Ha a Föld felszínének közelében a testek a 1 ill. a 2 gyorsulással szabadesést végeznek a rájuk ható nehézségi erő hatására, akkor felírhatjuk:

A tehetetlen és a súlyos tömeg Amennyiben a 1 = a 2 = g, az egyenletek jobb és baloldalait egymással elosztva kapjuk: Kísérleti igazolása: Eötvös Loránd, rendkívül érzékeny torziós ingájával 1 : 200 000 pontossággal mutatta meg azonosságukat. A tehetetlen és súlyos tömeg egyenlősége teszi lehetővé a súlymérésen alapuló tömegmérést.

Munka, energia