Five criteria for physical implementation of a quantum

Five criteria for physical implementation of a quantum computer 1. Well defined extendible qubit array -stable memory 2. Preparable in the “ 000…” state 3. Long decoherence time (>104 operation time) 4. Universal set of gate operations 5. Single-quantum measurements D. P. Di. Vincenzo, in Mesoscopic Electron Transport, eds. Sohn, Kowenhoven, Schoen (Kluwer 1997), p. 657, cond-mat/9612126; “The Physical Implementation of Quantum Computation, ” Fort. der Physik 48, 771 (2000), quant-ph/0002077.

Five criteria for physical implementation of a quantum computer & quantum communications 1. Well defined extendible qubit array -stable memory 2. Preparable in the “ 000…” state 3. Long decoherence time (>104 operation time) 4. Universal set of gate operations 5. Single-quantum measurements 6. Interconvert stationary and flying qubits 7. Transmit flying qubits from place to place

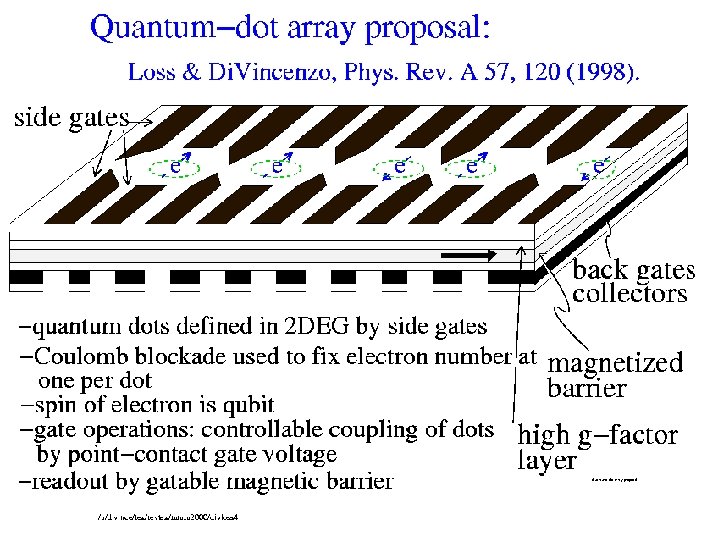
Quantum-dot array proposal

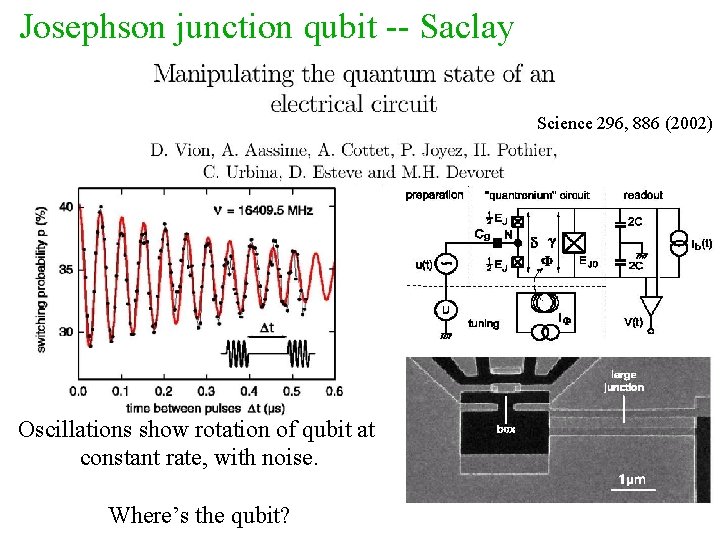
Josephson junction qubit -- Saclay Science 296, 886 (2002) Oscillations show rotation of qubit at constant rate, with noise. Where’s the qubit?

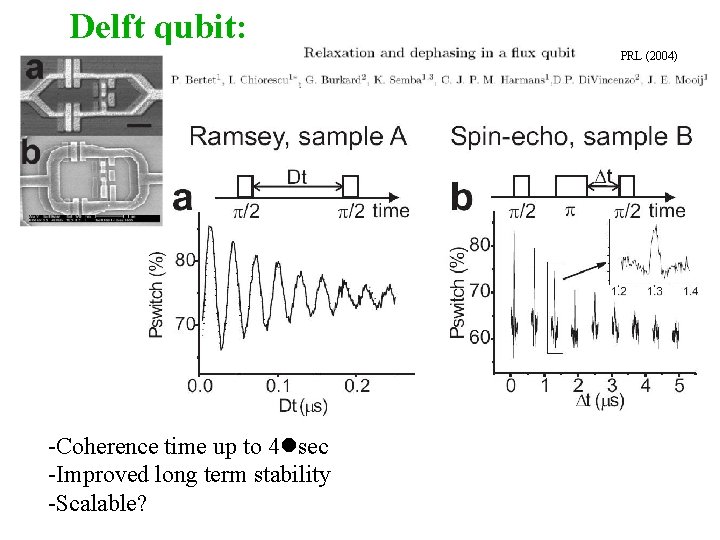
Delft qubit: PRL (2004) small -Coherence time up to 4 lsec -Improved long term stability -Scalable?

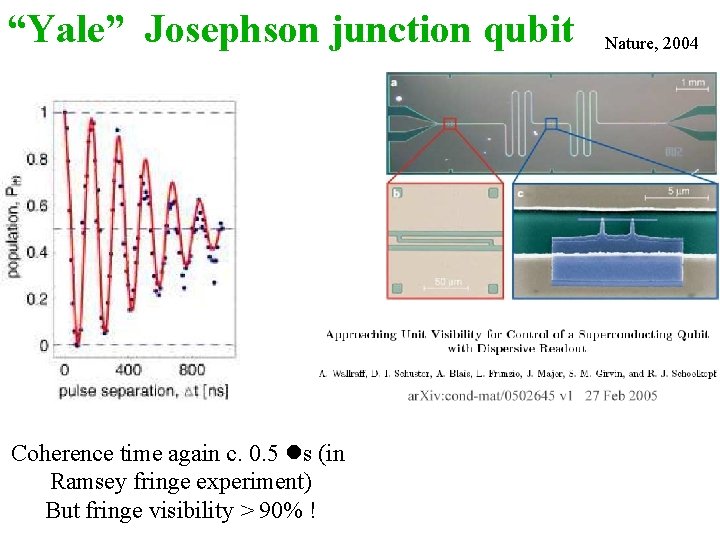
“Yale” Josephson junction qubit Coherence time again c. 0. 5 ls (in Ramsey fringe experiment) But fringe visibility > 90% ! Nature, 2004

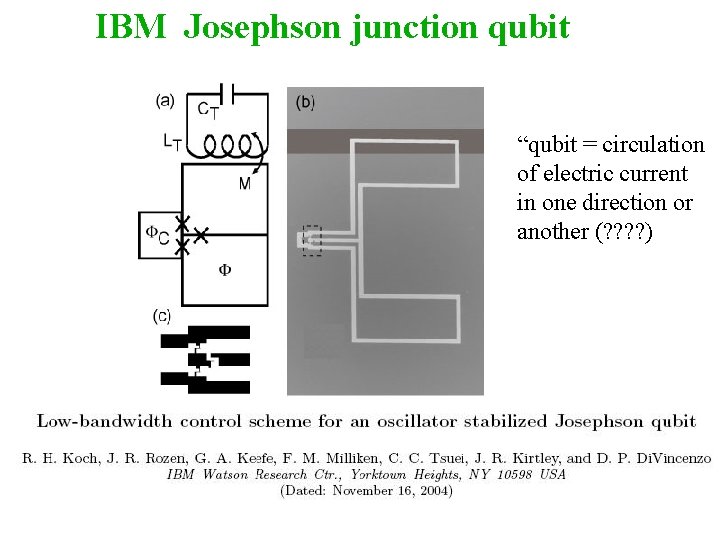
IBM Josephson junction qubit 1 “qubit = circulation of electric current in one direction or another (? ? )

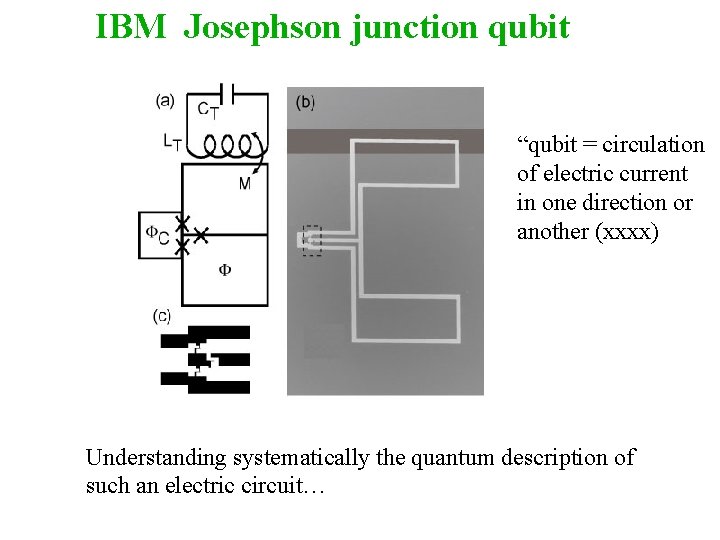
IBM Josephson junction qubit “qubit = circulation of electric current in one direction or another (xxxx) Understanding systematically the quantum description of such an electric circuit…

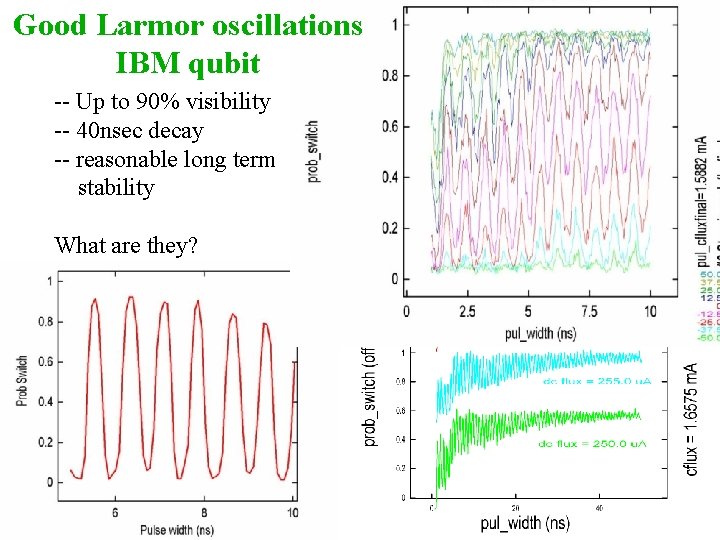
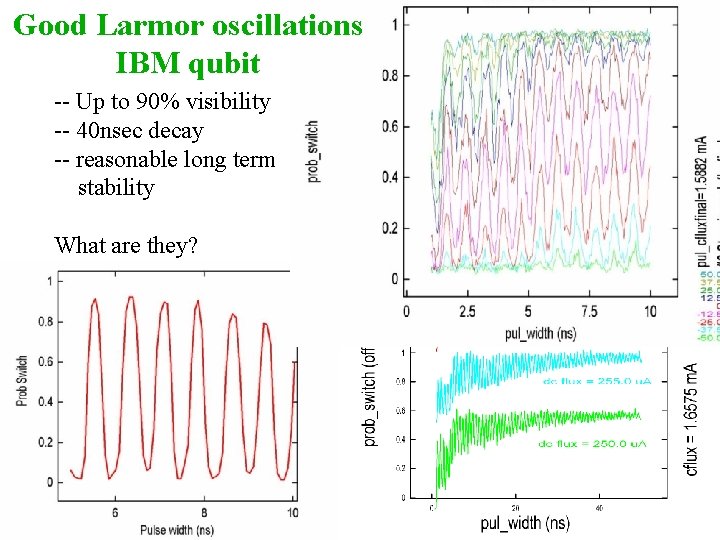
Good Larmor oscillations IBM qubit -- Up to 90% visibility -- 40 nsec decay -- reasonable long term stability What are they? small

small Simple electric circuit… L C harmonic oscillator with resonant frequency Quantum mechanically, like a kind of atom (with harmonic potential): x is any circuit variable (capacitor charge/current/voltage, Inductor flux/current/voltage) That is to say, it is a “macroscopic” variable that is being quantized.

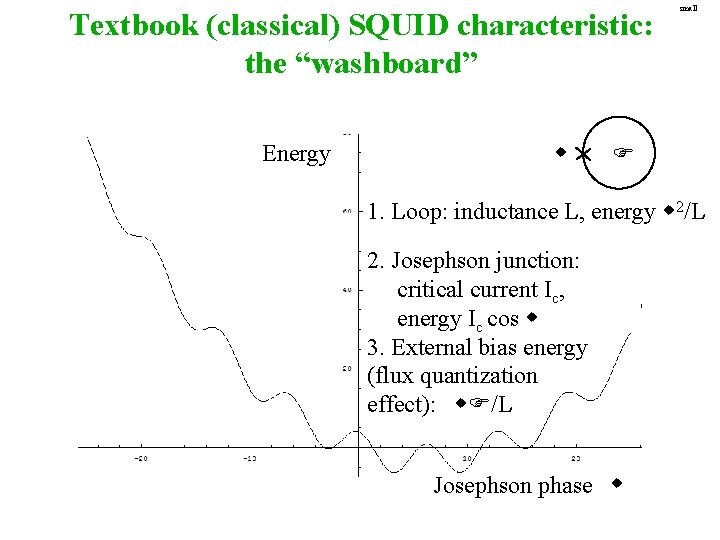
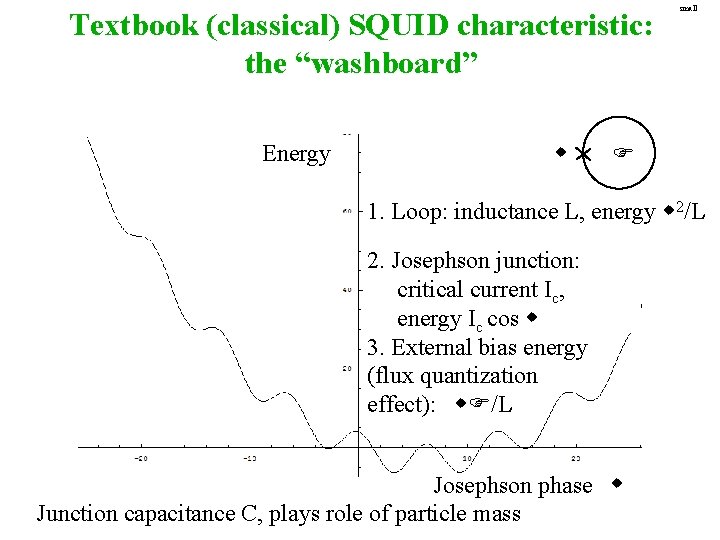
Textbook (classical) SQUID characteristic: the “washboard” Energy w small F 1. Loop: inductance L, energy w 2/L 2. Josephson junction: critical current Ic, energy Ic cos w 3. External bias energy (flux quantization effect): w. F/L Josephson phase w

Textbook (classical) SQUID characteristic: the “washboard” Energy w small F 1. Loop: inductance L, energy w 2/L 2. Josephson junction: critical current Ic, energy Ic cos w 3. External bias energy (flux quantization effect): w. F/L Josephson phase w Junction capacitance C, plays role of particle mass

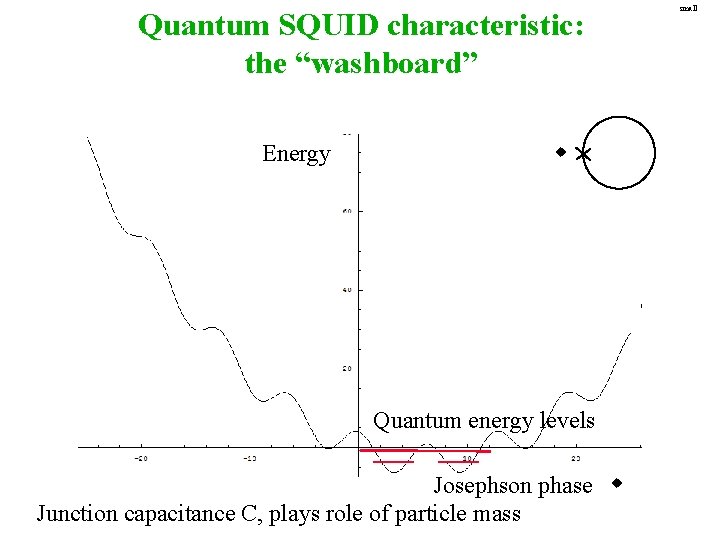
Quantum SQUID characteristic: the “washboard” Energy w Quantum energy levels Josephson phase w Junction capacitance C, plays role of particle mass small

But we will need to learn to deal with… small --Josephson junctions --current sources --resistances and impedances --mutual inductances --non-linear circuit elements? G. Burkard, R. H. Koch, and D. P. Di. Vincenzo, “Multi-level quantum description of decoherence in superconducting flux qubits, ” Phys. Rev. B 69, 064503 (2004); cond-mat/0308025.

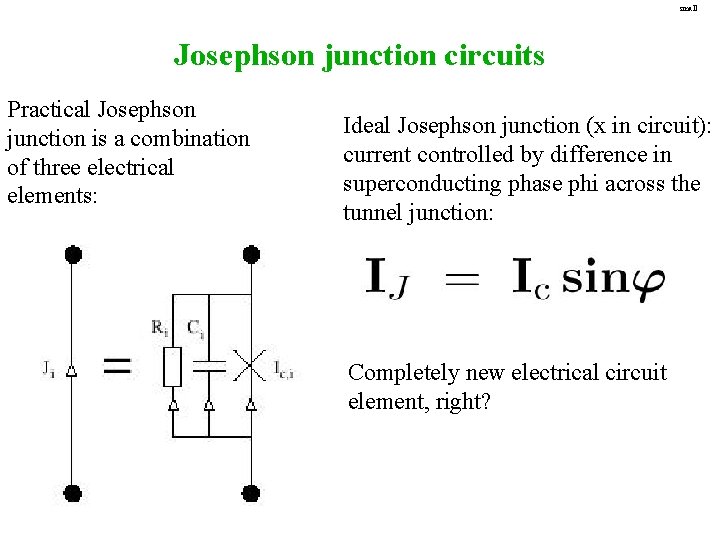
small Josephson junction circuits Practical Josephson junction is a combination of three electrical elements: Ideal Josephson junction (x in circuit): current controlled by difference in superconducting phase phi across the tunnel junction: Completely new electrical circuit element, right?

small not really… What’s an inductor (linear or nonlinear)? (instantaneous) Ideal Josephson junction: is the magnetic flux produced by the inductor is the superconducting phase difference across the barrier (Faraday) (Josephson’s second law) flux quantum

not really… What’s an inductor (linear or nonlinear)? Ideal Josephson junction: is the magnetic flux produced by the inductor is the superconducting phase difference across the barrier (Faraday) (Josephson’s second law) Phenomenologically, Josephson junctions are non-linear inductors. small

small So, we now do the systematic quantum theory

small Strategy: correspondence principle --Write circuit equations of motion: these are equations of classical mechanics --Technical challenge: it is a classical mechanics with constraints; must find the “unconstrained” set of circuit variables --find a Hamiltonian/Lagrangian from which these classical equations of motion arise --then, quantize! NB: no BCS theory, no microscopics – this is “phenomenological”, But based on sound general principles.

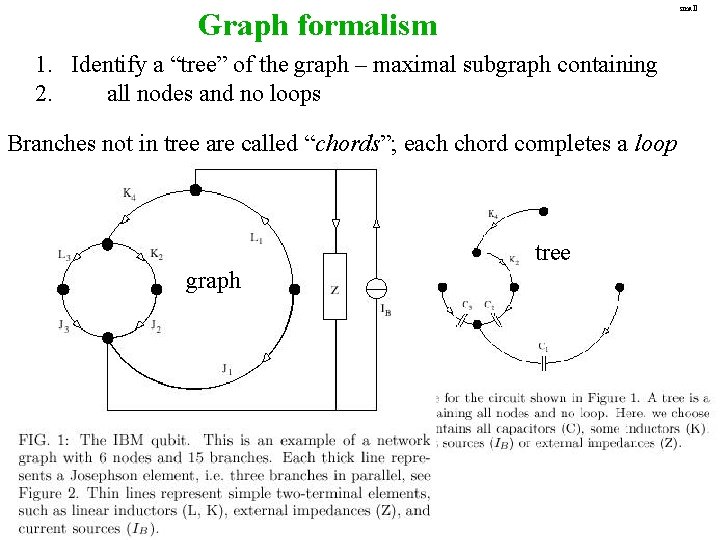
small Graph formalism 1. Identify a “tree” of the graph – maximal subgraph containing 2. all nodes and no loops Branches not in tree are called “chords”; each chord completes a loop tree graph

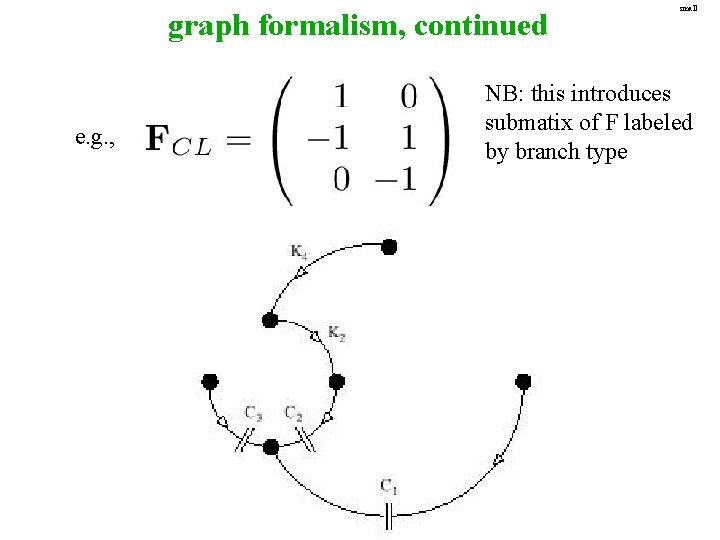
graph formalism, continued e. g. , small NB: this introduces submatix of F labeled by branch type

Circuit equations in the graph formalism: small Kirchhoff’s current laws: V: I: F: Kirchhoff’s voltage laws: branch voltages branch currents external fluxes threading loops

With all this, the equation of motion: small The tricky part: what are the independent degrees of freedom? If there are no capacitor-only loops (i. e. , every loop has an inductance), then the independent variables are just the Josephson phases, and the “capacitor phases” (time integral of the voltage): “just like” the biassed Josephson junction, except…

the equation of motion (continued): All are complicated but straightforward functions of the topology (F matrices) and the inductance matrix small

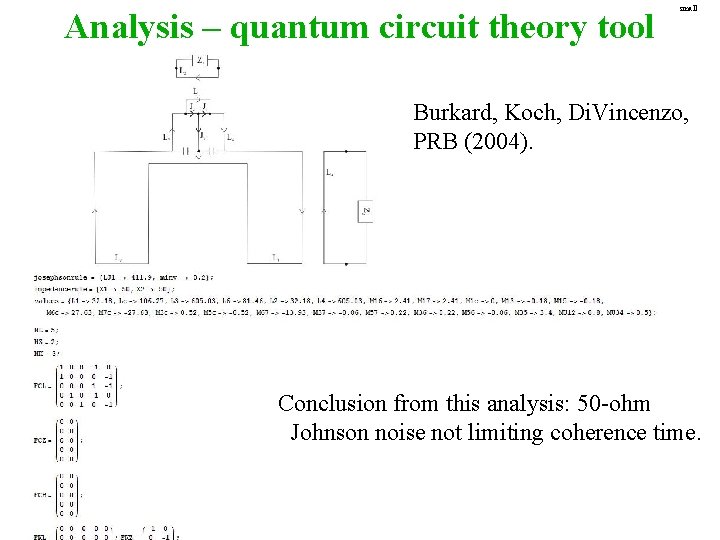
Analysis – quantum circuit theory tool small Burkard, Koch, Di. Vincenzo, PRB (2004). Conclusion from this analysis: 50 -ohm Johnson noise not limiting coherence time.

the equation of motion (continued): small The lossless parts of this equation arise from a simple Hamiltonian: H; U=exp(i. Ht)

the equation of motion (continued): The lossy parts of this equation arise from a bath Hamiltonian, Via a Caldeira-Leggett treatment: small

Connecting Cadeira Leggett to circuit theory: small

Overview of what we’ve accomplished: We have a systematic derivation of a general system-bath Hamiltonian. From this we can proceed to obtain: • system master equation • spin-boson approximation (two level) • Born-Markov approximation -> Bloch Redfield theory • golden rule (decay rates) • leakage rates For example: small

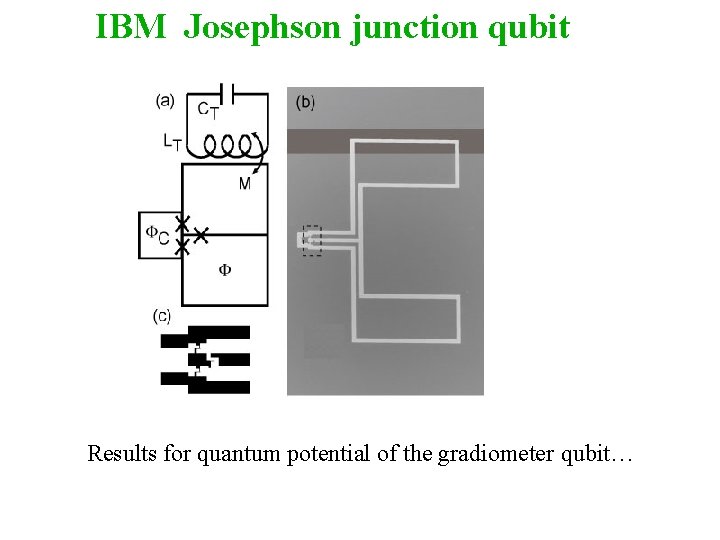
IBM Josephson junction qubit Results for quantum potential of the gradiometer qubit…

IBM Josephson junction qubit: potential landscape --Double minimum evident (red streak) --Third direction very “stiff”

IBM Josephson junction qubit: effective 1 -D potential x --treat two transverse directions (blue) as “fast” coordinates using Born-Oppenheimer

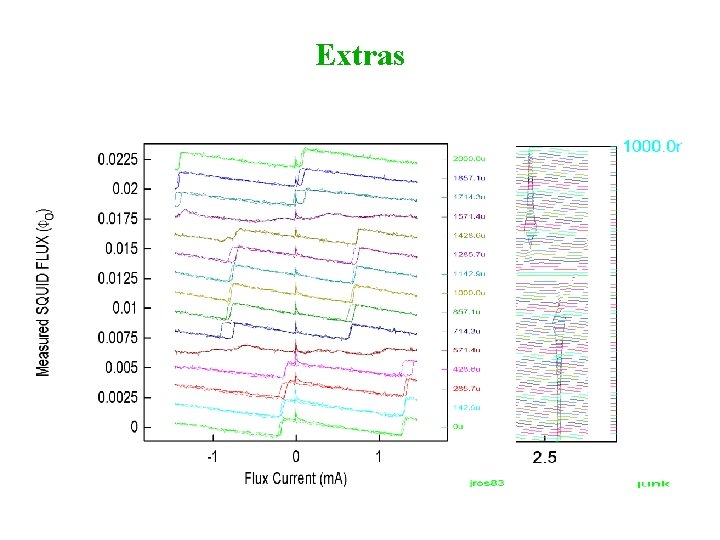
Extras

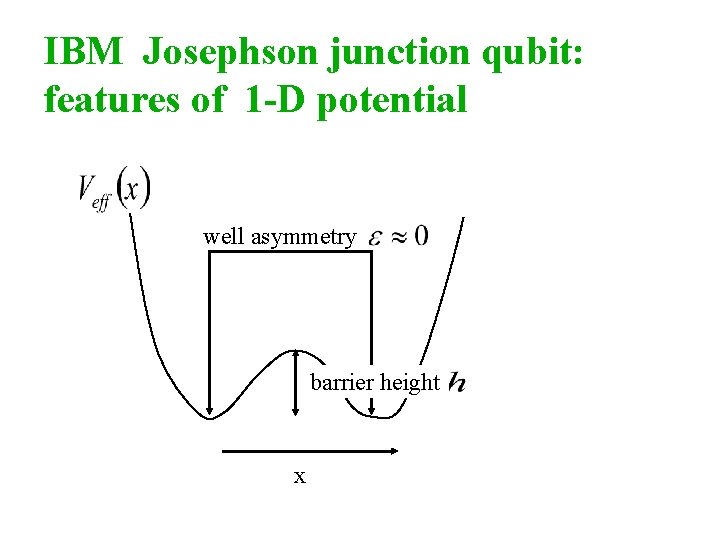
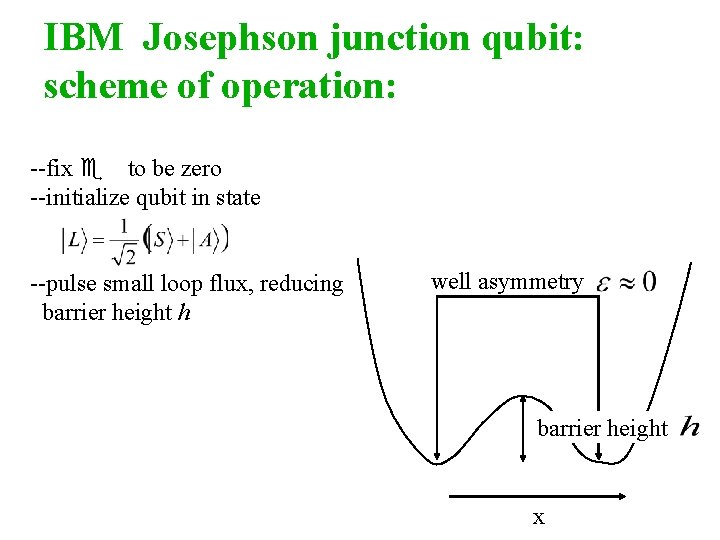
IBM Josephson junction qubit: features of 1 -D potential well asymmetry barrier height x

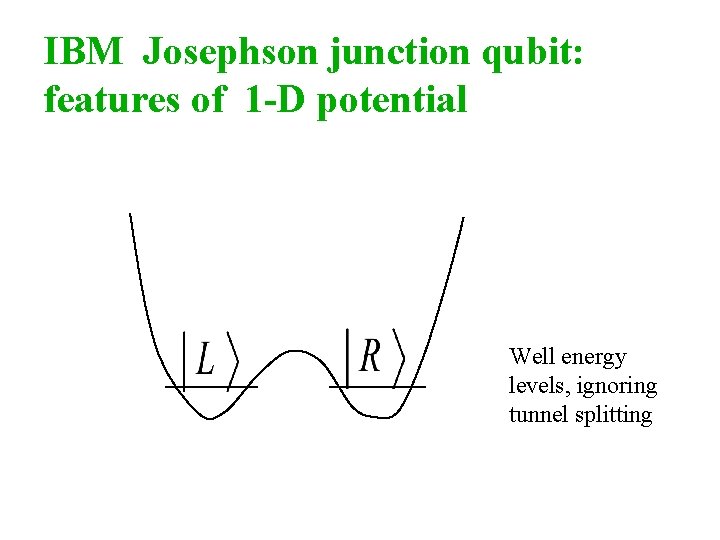
IBM Josephson junction qubit: features of 1 -D potential Well energy levels, ignoring tunnel splitting

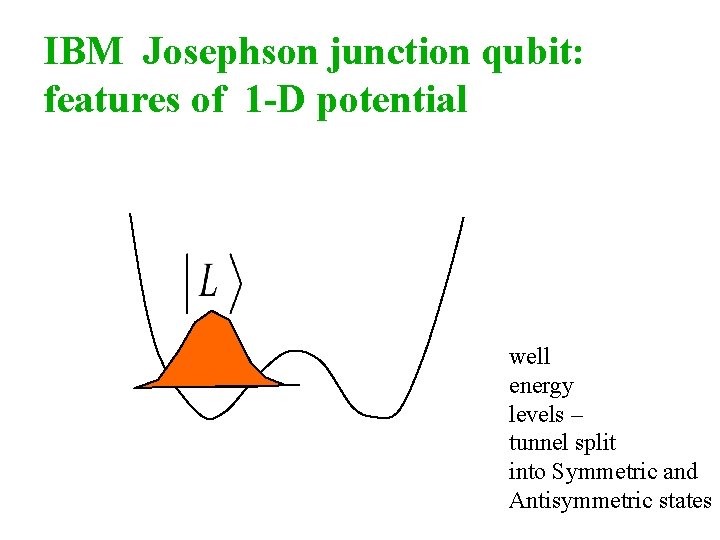
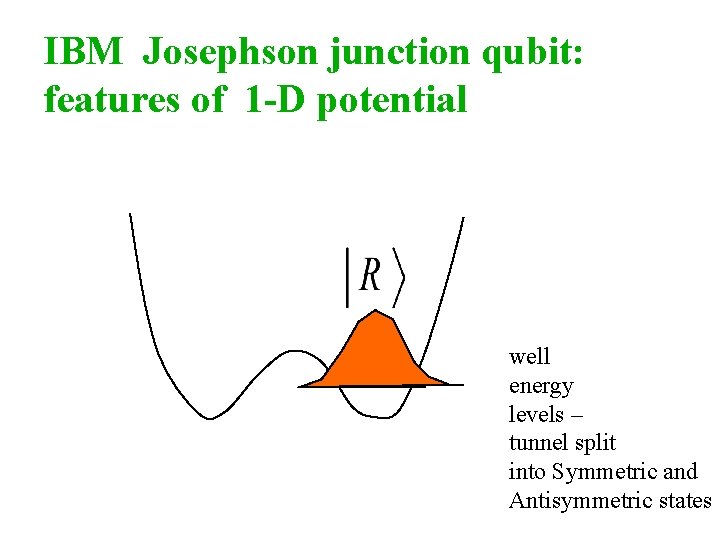
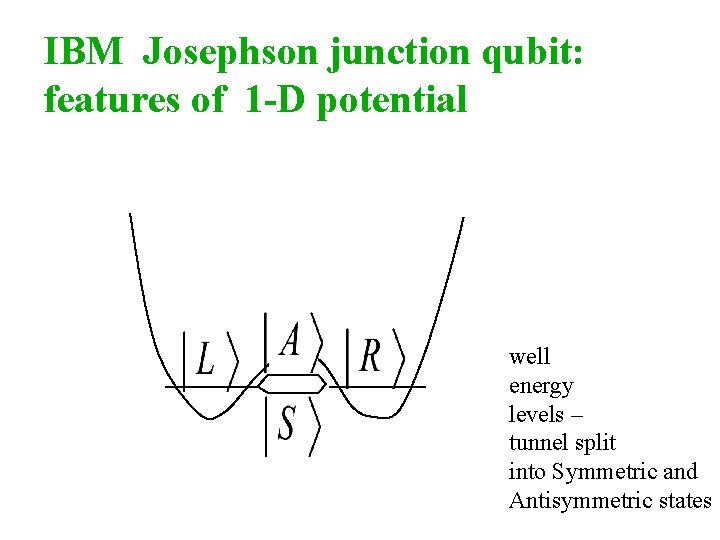
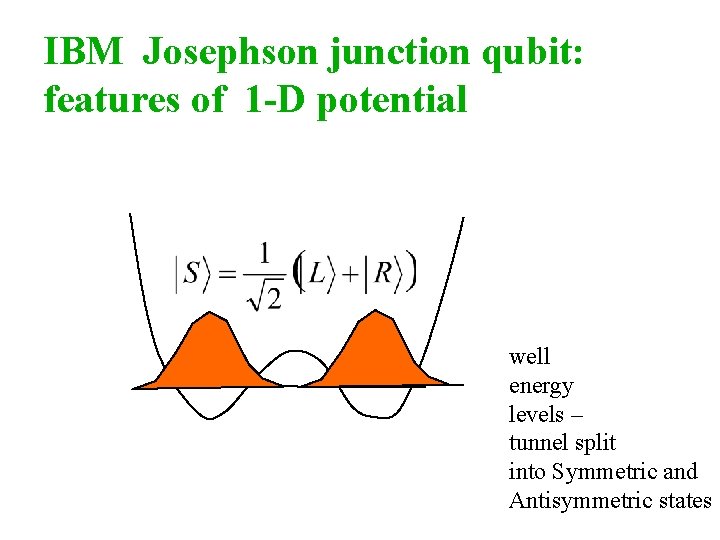
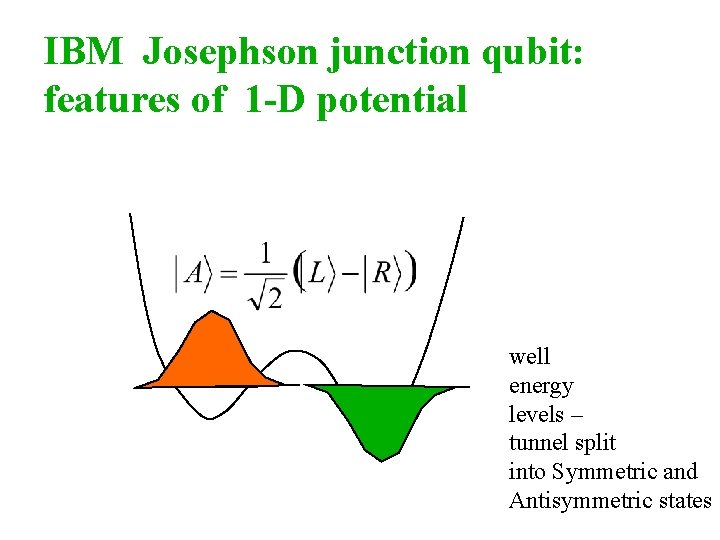
IBM Josephson junction qubit: features of 1 -D potential well energy levels – tunnel split into Symmetric and Antisymmetric states

IBM Josephson junction qubit: features of 1 -D potential well energy levels – tunnel split into Symmetric and Antisymmetric states

IBM Josephson junction qubit: features of 1 -D potential well energy levels – tunnel split into Symmetric and Antisymmetric states

IBM Josephson junction qubit: features of 1 -D potential well energy levels – tunnel split into Symmetric and Antisymmetric states

IBM Josephson junction qubit: features of 1 -D potential well energy levels – tunnel split into Symmetric and Antisymmetric states

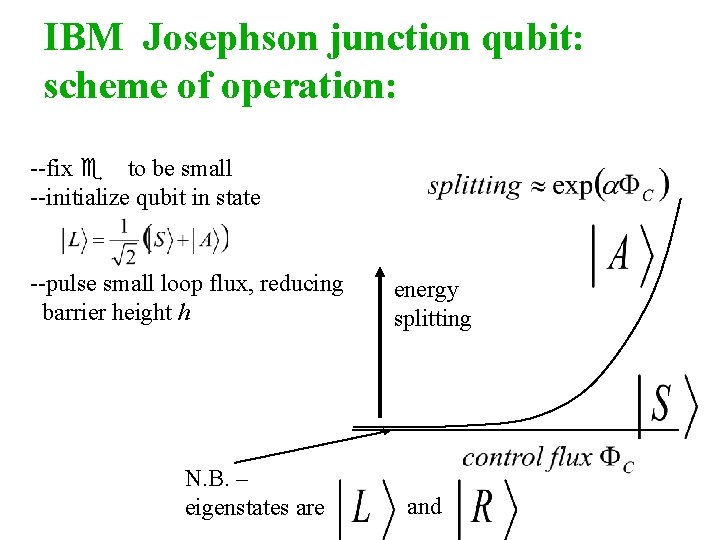
IBM Josephson junction qubit: scheme of operation: --fix e to be zero --initialize qubit in state --pulse small loop flux, reducing barrier height h well asymmetry barrier height x

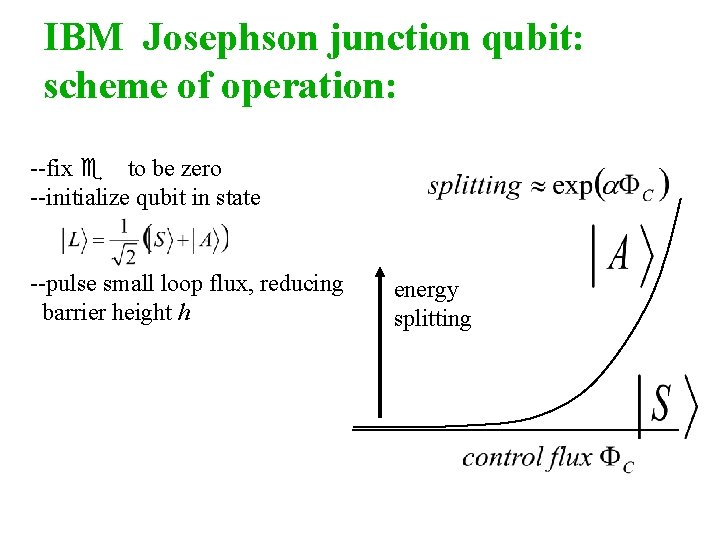
IBM Josephson junction qubit: scheme of operation: --fix e to be zero --initialize qubit in state --pulse small loop flux, reducing barrier height h energy splitting

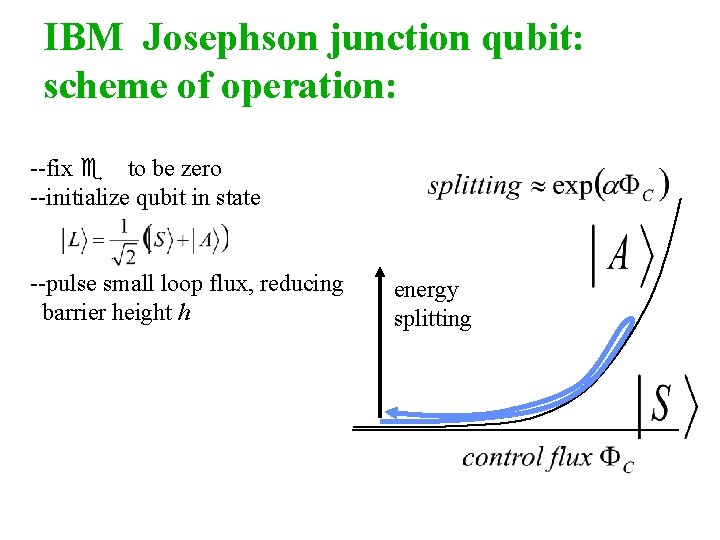
IBM Josephson junction qubit: scheme of operation: --fix e to be zero --initialize qubit in state --pulse small loop flux, reducing barrier height h energy splitting

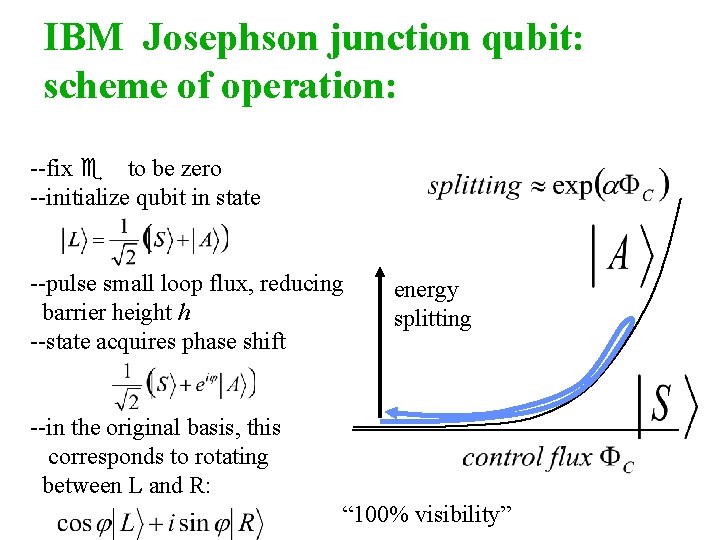
IBM Josephson junction qubit: scheme of operation: --fix e to be zero --initialize qubit in state --pulse small loop flux, reducing barrier height h --state acquires phase shift energy splitting --in the original basis, this corresponds to rotating between L and R: “ 100% visibility”

IBM Josephson junction qubit: scheme of operation: --fix e to be small --initialize qubit in state --pulse small loop flux, reducing barrier height h N. B. – eigenstates are energy splitting and

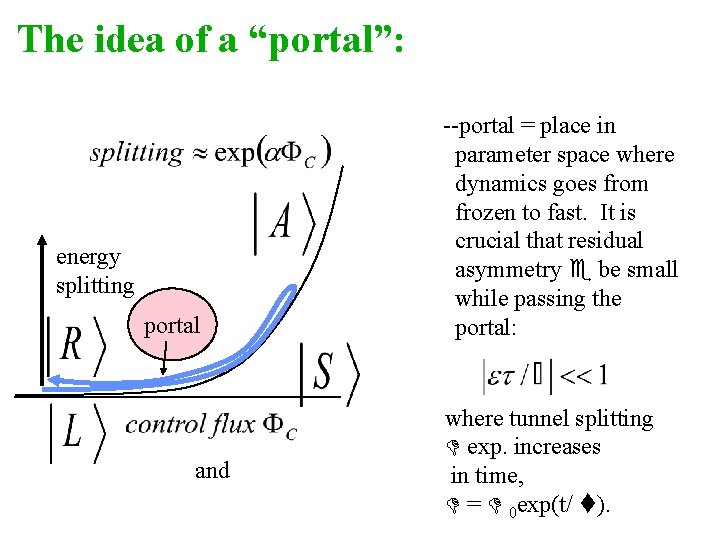
The idea of a “portal”: energy splitting portal and --portal = place in parameter space where dynamics goes from frozen to fast. It is crucial that residual asymmetry e be small while passing the portal: where tunnel splitting D exp. increases in time, D = D 0 exp(t/ t).

IBM Josephson junction qubit: analyzing the “portal” --e cannot be fixed to be exactly zero --full non-adiabatic time evolution of Schrodinger equation with fixed e and tunnel splitting D exponentially increasing in time, D = D 0 exp(t/ t), can be solved exactly … the spinor wavefunction is Which means that the visibility is high so long as

Problem: • Tunnel splitting exponentially sensitive to control flux • Flux noise will seriously impair visiblity • Solution

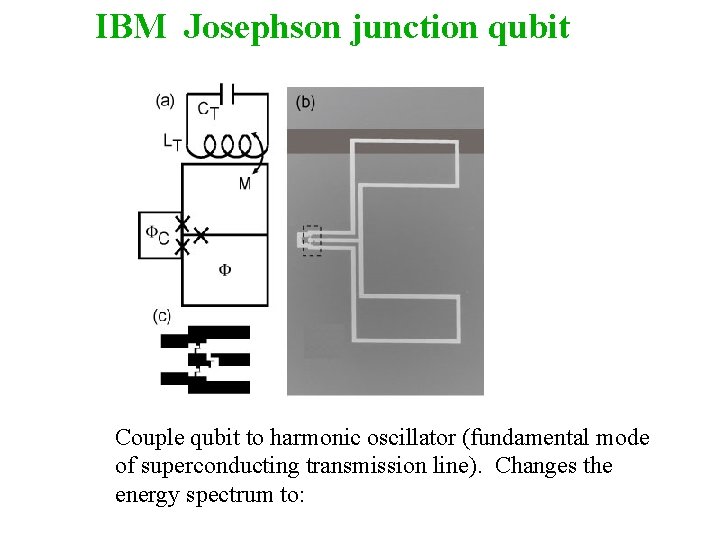
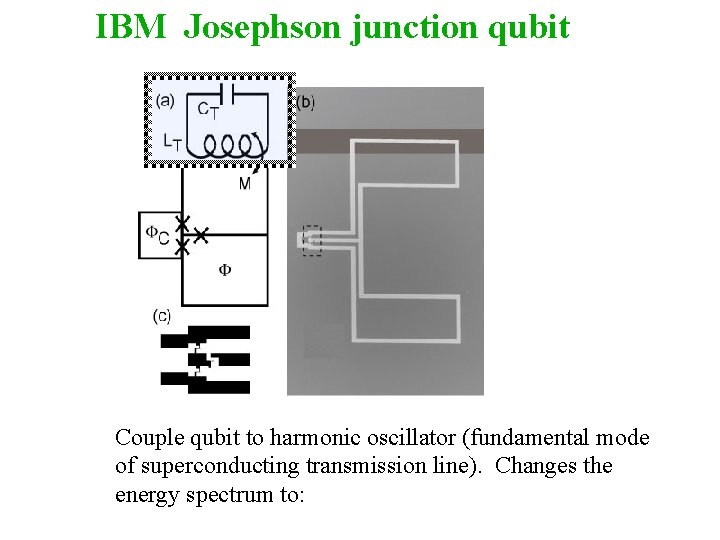
IBM Josephson junction qubit Couple qubit to harmonic oscillator (fundamental mode of superconducting transmission line). Changes the energy spectrum to:

IBM Josephson junction qubit Couple qubit to harmonic oscillator (fundamental mode of superconducting transmission line). Changes the energy spectrum to:

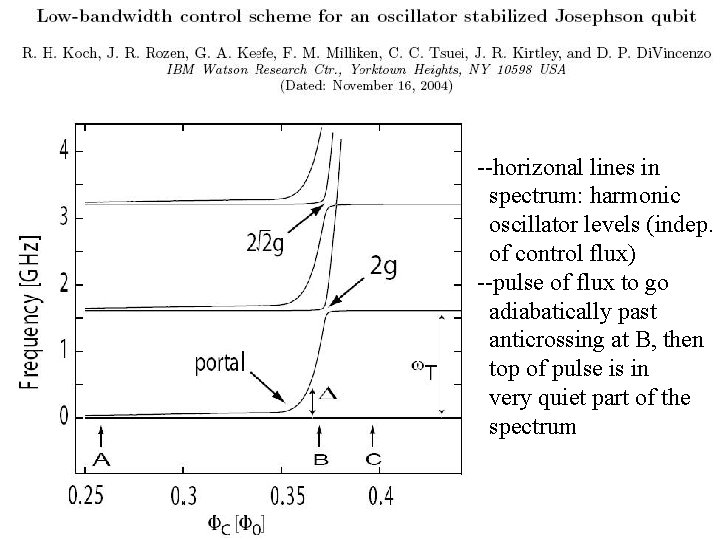
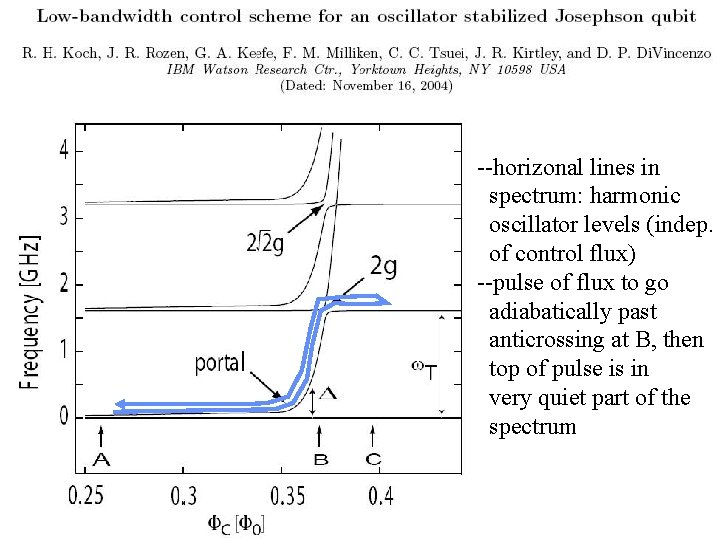
s --horizonal lines in spectrum: harmonic oscillator levels (indep. of control flux) --pulse of flux to go adiabatically past anticrossing at B, then top of pulse is in very quiet part of the spectrum

s --horizonal lines in spectrum: harmonic oscillator levels (indep. of control flux) --pulse of flux to go adiabatically past anticrossing at B, then top of pulse is in very quiet part of the spectrum

Good Larmor oscillations IBM qubit -- Up to 90% visibility -- 40 nsec decay -- reasonable long term stability What are they? small

Overview: small 1. A “user friendly” procedure: automates the assessment of different circuit designs 2. Gives some new views of existing circuits and their analysis 3. A “meta-theory” – aids the development of approximate theories at many levels 4. BUT – it is the “orthodox” theory of decoherence – exotic effects like nuclear-spin dephasing not captured by this analysis.

Adiabatic Q. C. 1. 2. 3. 4. 5. Farhi et al idea Feynmann ’ 84: wavepacket propagation idea Aharonov et al: connection to adiabatic Q. C. 4 -locality, 2 -locality – effective Hamiltonians Problem – polynomial gap… Topological Q. C. 1. 2. 3. 4. Kitaev: toric code Kitaev: anyons: even more complex Hamiltonian… Universality: honeycomb lattice with field Fractional quantum Hall states: 5/2, 13/5 small