Fitting of cooling measurements results Recycler department meeting

Fitting of cooling measurements results Recycler department meeting June 14, 2006 A. Shemyakin, A. Burov, S. Nagaitsev, L. Prost

Outline § Electron beam parameters Ø Model with secondary electrons § Fitting drag rate measurements to formulae § Comparing with cooling rates 2

Electron beam parameters Following electron beam parameters are important for the cooling rate: § Longitudinal temperature § Transverse temperature § Current density 3

Electron beam parameters- longitudinal temperature § The cooling process is determined by an effective energy spread consisting primarily of two components, the electron energy spread at a fixed time and the Pelletron voltage ripple Ø The energy spread is determined by IBS (the main contributor) and by density fluctuations at the cathode. According to simulations, at currents 0. 1 – 0. 5 A the energy spread is 70 – 150 e. V. Ø The Pelletron voltage ripple is 200 - 300 V r. m. s. (probably, fluctuates from day to day). The main frequency is 1. 8 Hz, which is much shorter than a cooling time. Ø Hence, the effective energy spread is equal to these two effects added in quadratures. Ø There is a significant (~50%) inconsistency in present measurements of the HV noise 4

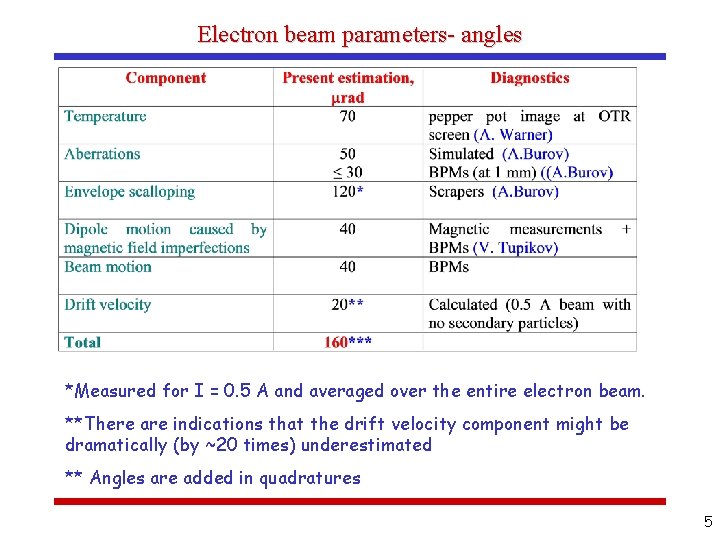
Electron beam parameters- angles *Measured for I = 0. 5 A and averaged over the entire electron beam. **There are indications that the drift velocity component might be dramatically (by ~20 times) underestimated ** Angles are added in quadratures 5

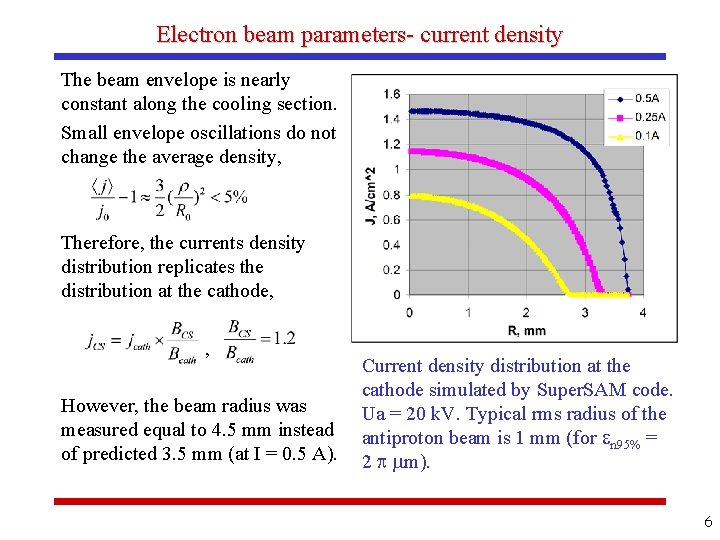
Electron beam parameters- current density The beam envelope is nearly constant along the cooling section. Small envelope oscillations do not change the average density, Therefore, the currents density distribution replicates the distribution at the cathode, , However, the beam radius was measured equal to 4. 5 mm instead of predicted 3. 5 mm (at I = 0. 5 A). Current density distribution at the cathode simulated by Super. SAM code. Ua = 20 k. V. Typical rms radius of the antiproton beam is 1 mm (for n 95% = 2 m). 6

Discrepancy with beam size measurements § Two possible explanations of too large beam size measured in the cooling section with scrapers: Ø a beam halo Ø secondary electrons 7

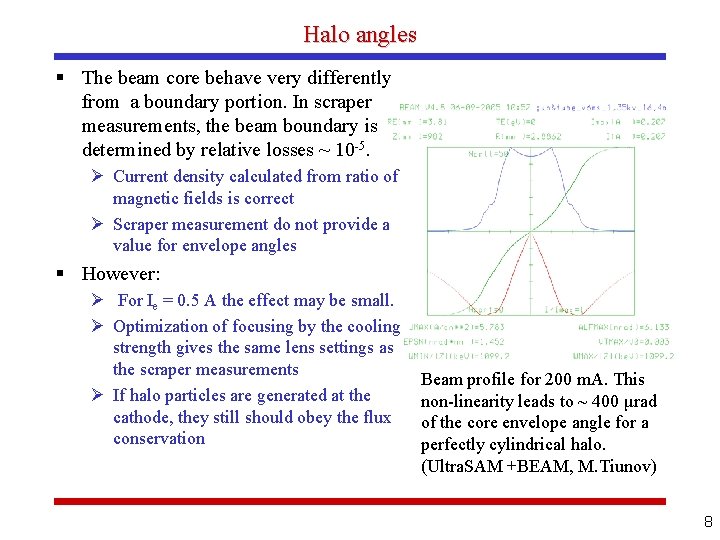
Halo angles § The beam core behave very differently from a boundary portion. In scraper measurements, the beam boundary is determined by relative losses ~ 10 -5. Ø Current density calculated from ratio of magnetic fields is correct Ø Scraper measurement do not provide a value for envelope angles § However: Ø For Ie = 0. 5 A the effect may be small. Ø Optimization of focusing by the cooling strength gives the same lens settings as the scraper measurements Ø If halo particles are generated at the cathode, they still should obey the flux conservation Beam profile for 200 m. A. This non-linearity leads to ~ 400 μrad of the core envelope angle for a perfectly cylindrical halo. (Ultra. SAM +BEAM, M. Tiunov) 8

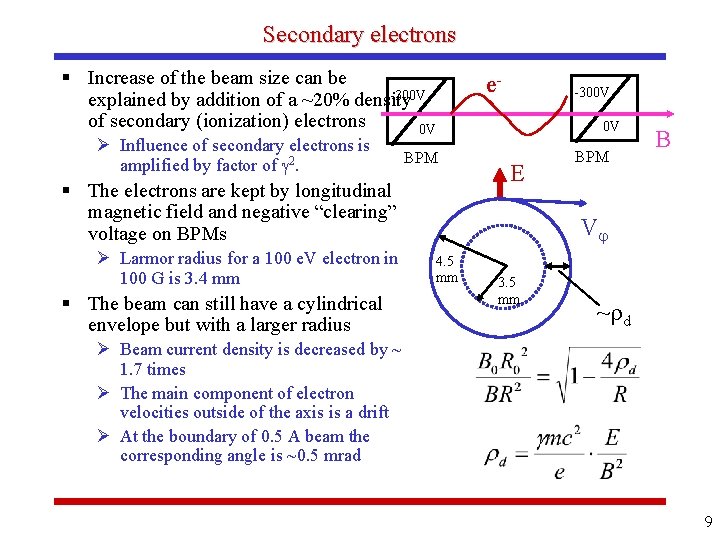
Secondary electrons § Increase of the beam size can be -300 V explained by addition of a ~20% density of secondary (ionization) electrons 0 V Ø Influence of secondary electrons is amplified by factor of 2. BPM § The electrons are kept by longitudinal magnetic field and negative “clearing” voltage on BPMs Ø Larmor radius for a 100 e. V electron in 100 G is 3. 4 mm § The beam can still have a cylindrical envelope but with a larger radius e- -300 V 0 V E BPM B V 4. 5 mm 3. 5 mm ~ d Ø Beam current density is decreased by ~ 1. 7 times Ø The main component of electron velocities outside of the axis is a drift Ø At the boundary of 0. 5 A beam the corresponding angle is ~0. 5 mrad 9

Electron angles in cooling rate measurements § In the cooling rate measurements, a typical antiproton beam size is Rp= 1 mm. Components proportional to radius contribute to the total angle as where 0 is the rms angle on axis. § From the summary table, 0 ~ 90 rad. § For the model with secondary electrons, m ~ 460 rad at Re= 4. 5 mm, and t ~ 110 rad. 10

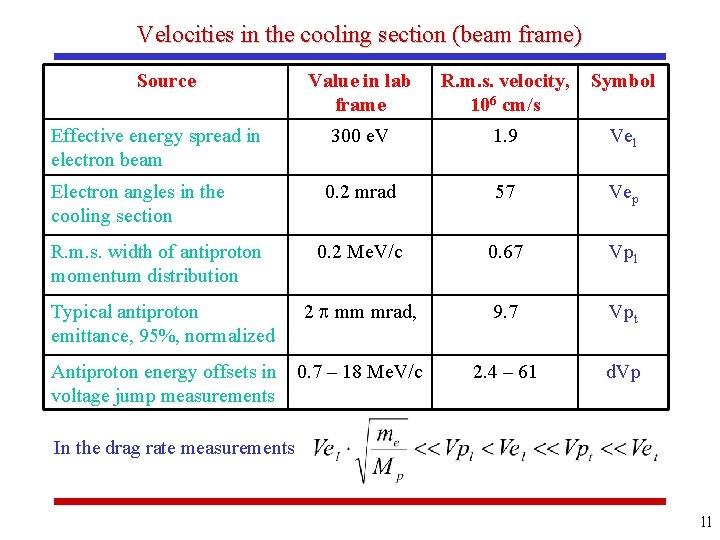
Velocities in the cooling section (beam frame) Source Value in lab frame R. m. s. velocity, 106 cm/s Symbol 300 e. V 1. 9 Vel 0. 2 mrad 57 Vep 0. 2 Me. V/c 0. 67 Vpl Typical antiproton emittance, 95%, normalized 2 mm mrad, 9. 7 Vpt Antiproton energy offsets in voltage jump measurements 0. 7 – 18 Me. V/c 2. 4 – 61 d. Vp Effective energy spread in electron beam Electron angles in the cooling section R. m. s. width of antiproton momentum distribution In the drag rate measurements 11

Measurements of the longitudinal cooling force § Special requirements: Ø Ø § Small number of pbars (1 -5 × 1010) Coasting beam Narrow momentum distribution (< 0. 2 Me. V/c) Low transverse emittances (< 3 mm mrad, 95%, normalized) From equilibrium width (for small momentum offsets) Ø Reach equilibrium with e-cooling Ø Turn off e-cooling and measure the diffusion rate § Voltage jump measurement (for momentum offsets > 1 Me. V/c) Ø Reach equilibrium with electron beam Ø Change electron beam energy Ø Record dynamics of the average pbar momentum 12

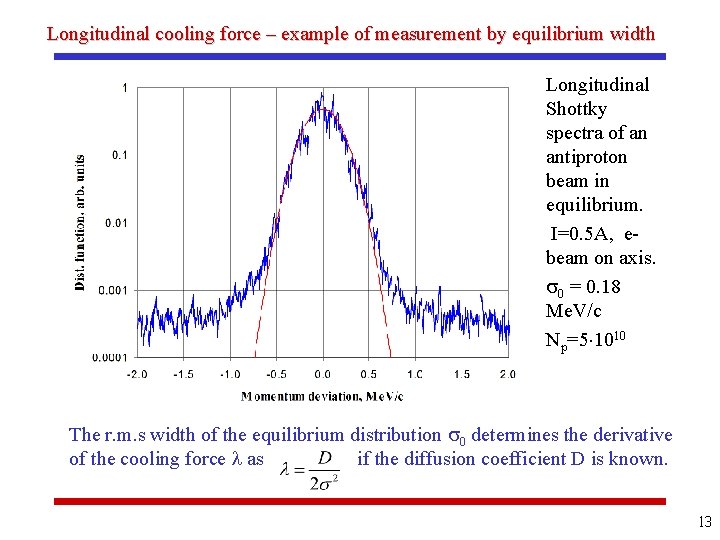
Longitudinal cooling force – example of measurement by equilibrium width Longitudinal Shottky spectra of an antiproton beam in equilibrium. I=0. 5 A, ebeam on axis. 0 = 0. 18 Me. V/c Np=5 1010 The r. m. s width of the equilibrium distribution 0 determines the derivative of the cooling force as if the diffusion coefficient D is known. 13

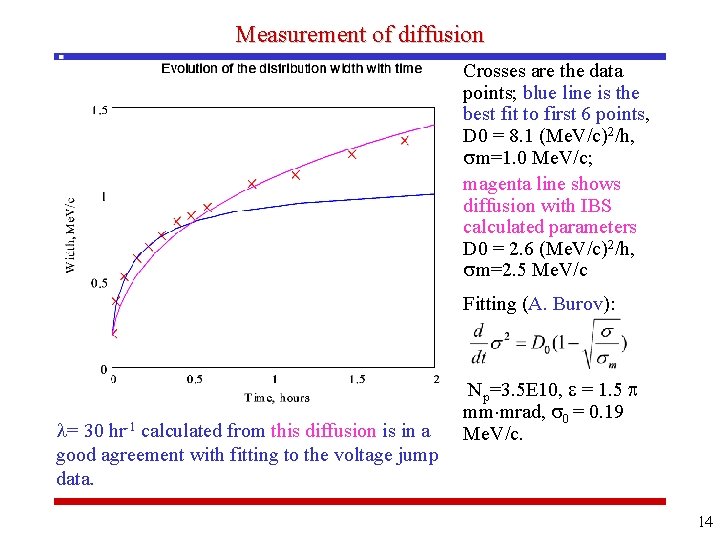
Measurement of diffusion Crosses are the data points; blue line is the best fit to first 6 points, D 0 = 8. 1 (Me. V/c)2/h, m=1. 0 Me. V/c; magenta line shows diffusion with IBS calculated parameters D 0 = 2. 6 (Me. V/c)2/h, m=2. 5 Me. V/c Fitting (A. Burov): = 30 hr-1 calculated from this diffusion is in a good agreement with fitting to the voltage jump data. Np=3. 5 E 10, = 1. 5 mm mrad, 0 = 0. 19 Me. V/c. 14

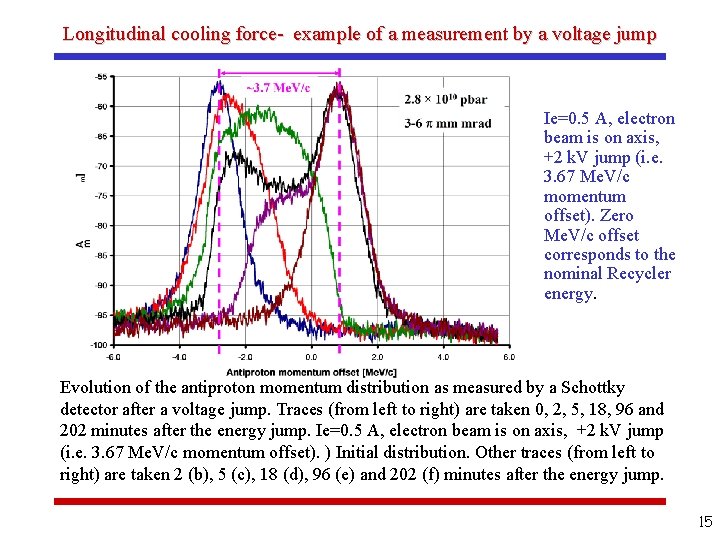
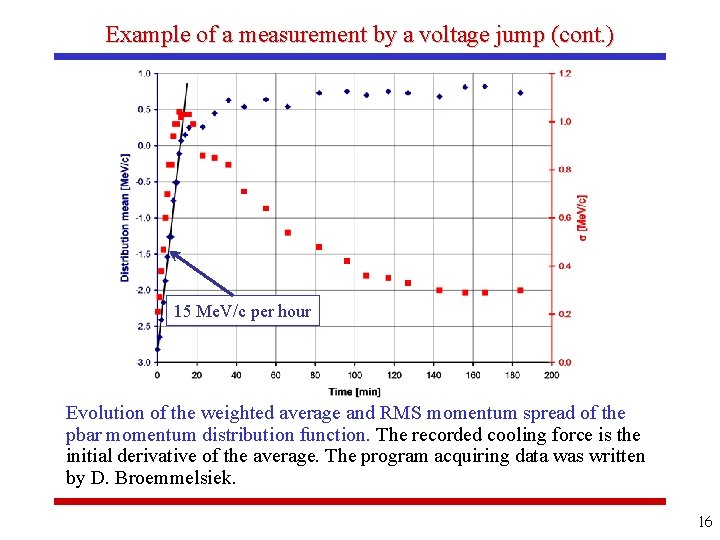
Longitudinal cooling force- example of a measurement by a voltage jump Ie=0. 5 A, electron beam is on axis, +2 k. V jump (i. e. 3. 67 Me. V/c momentum offset). Zero Me. V/c offset corresponds to the nominal Recycler energy. Evolution of the antiproton momentum distribution as measured by a Schottky detector after a voltage jump. Traces (from left to right) are taken 0, 2, 5, 18, 96 and 202 minutes after the energy jump. Ie=0. 5 A, electron beam is on axis, +2 k. V jump (i. e. 3. 67 Me. V/c momentum offset). ) Initial distribution. Other traces (from left to right) are taken 2 (b), 5 (c), 18 (d), 96 (e) and 202 (f) minutes after the energy jump. 15

Example of a measurement by a voltage jump (cont. ) 15 Me. V/c per hour Evolution of the weighted average and RMS momentum spread of the pbar momentum distribution function. The recorded cooling force is the initial derivative of the average. The program acquiring data was written by D. Broemmelsiek. 16

Non-magnetized model Ve, Vp- velocities of an antiproton and electrons, is Coulomb logarithm We assume a Gaussian distribution of the electron velocities with z and z standard deviations, and neglect transverse antiproton velocities. In simulations, the fitted parameters are the current density and r. m. s. values of the electron energy spread angles. Lab frame quantities For calculation of the longitudinal force, the transverse pbar velocities can be neglected. S. Nagaitsev approximated the integral so it can be dealt with in Math. Cad. 17

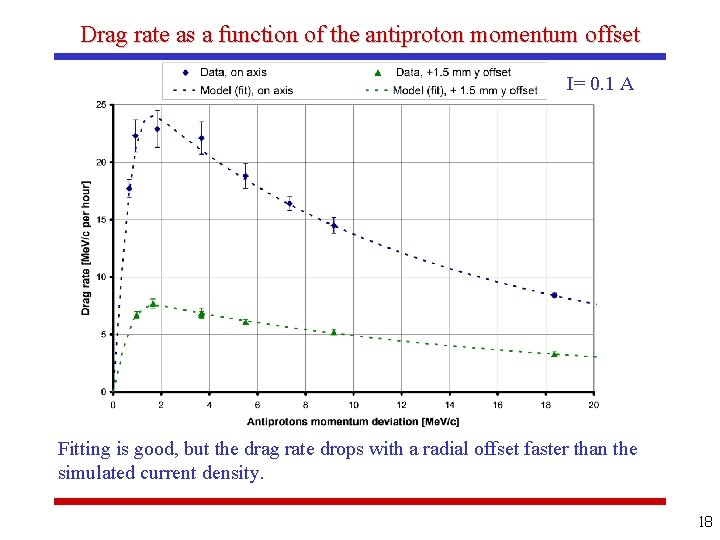
Drag rate as a function of the antiproton momentum offset I= 0. 1 A Fitting is good, but the drag rate drops with a radial offset faster than the simulated current density. 18

Interpretation of the radial dependence in the secondary electron model § A strong radial dependence can be explained in the model, where a large density of secondary electrons results in a drift rotation of the primary beam Ø Model: constant density of secondary electrons • Primary beam’s density profile is proportionally expanded Ø Azimuthal velocity is proportional to radius, Ø Transverse velocities are added in quadratures, § The drag force near maximum depends on density and transverse electron velocities as Ø where radial variation of the electron beam density is extrapolated by a parabola 19

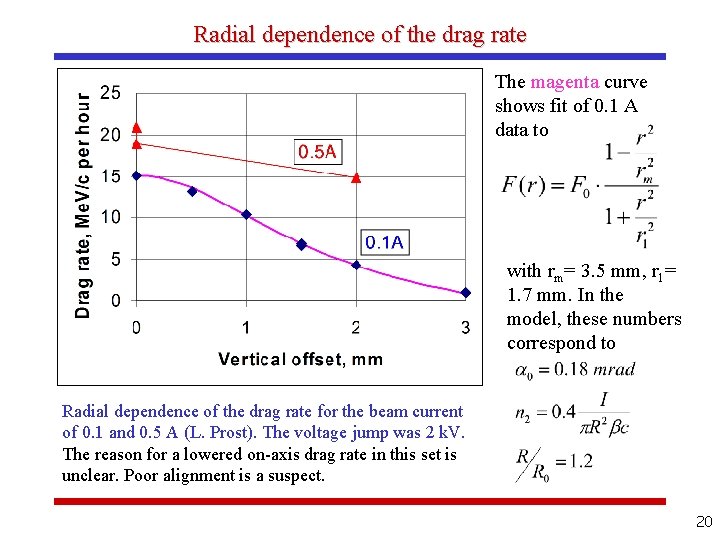
Radial dependence of the drag rate The magenta curve shows fit of 0. 1 A data to with rm= 3. 5 mm, r 1= 1. 7 mm. In the model, these numbers correspond to Radial dependence of the drag rate for the beam current of 0. 1 and 0. 5 A (L. Prost). The voltage jump was 2 k. V. The reason for a lowered on-axis drag rate in this set is unclear. Poor alignment is a suspect. 20

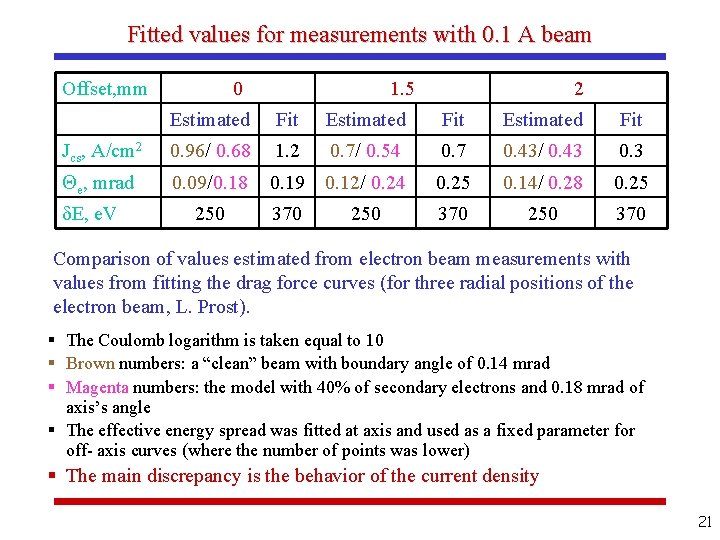
Fitted values for measurements with 0. 1 A beam Offset, mm 0 1. 5 2 Estimated Fit Jcs, A/cm 2 0. 96/ 0. 68 1. 2 0. 7/ 0. 54 0. 7 0. 43/ 0. 43 0. 3 e, mrad 0. 09/0. 18 0. 19 0. 12/ 0. 24 0. 25 0. 14/ 0. 28 0. 25 250 370 E, e. V Comparison of values estimated from electron beam measurements with values from fitting the drag force curves (for three radial positions of the electron beam, L. Prost). § The Coulomb logarithm is taken equal to 10 § Brown numbers: a “clean” beam with boundary angle of 0. 14 mrad § Magenta numbers: the model with 40% of secondary electrons and 0. 18 mrad of axis’s angle § The effective energy spread was fitted at axis and used as a fixed parameter for off- axis curves (where the number of points was lower) § The main discrepancy is the behavior of the current density 21

Antiproton tune shift § Antiproton tune shift on the electron beam : § For Ie= 0. 1 A, Re = 3 mm § For , § While memory tells that such tune shift has been observed, I did not find proofs neither in the log book nor in D 44. § Recent attempt to look at the tunes (S. Pruss) shown no effect, It is a significant contradiction to the model with secondary electrons. 22

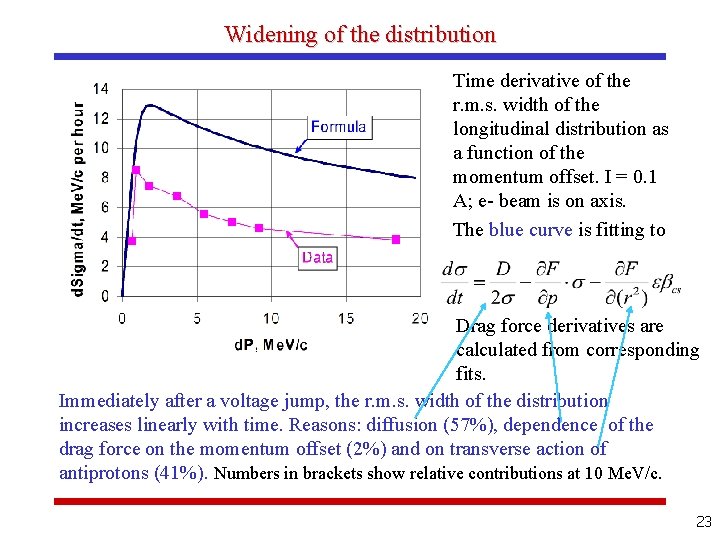
Widening of the distribution Time derivative of the r. m. s. width of the longitudinal distribution as a function of the momentum offset. I = 0. 1 A; e- beam is on axis. The blue curve is fitting to Drag force derivatives are calculated from corresponding fits. Immediately after a voltage jump, the r. m. s. width of the distribution increases linearly with time. Reasons: diffusion (57%), dependence of the drag force on the momentum offset (2%) and on transverse action of antiprotons (41%). Numbers in brackets show relative contributions at 10 Me. V/c. 23

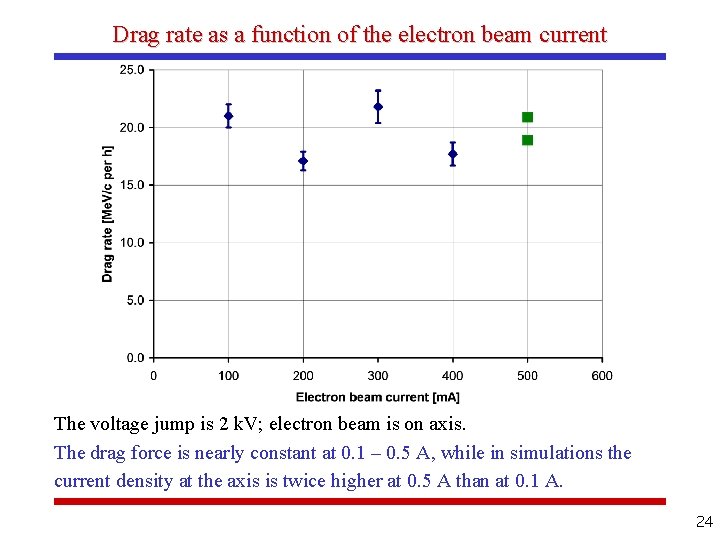
Drag rate as a function of the electron beam current The voltage jump is 2 k. V; electron beam is on axis. The drag force is nearly constant at 0. 1 – 0. 5 A, while in simulations the current density at the axis is twice higher at 0. 5 A than at 0. 1 A. 24

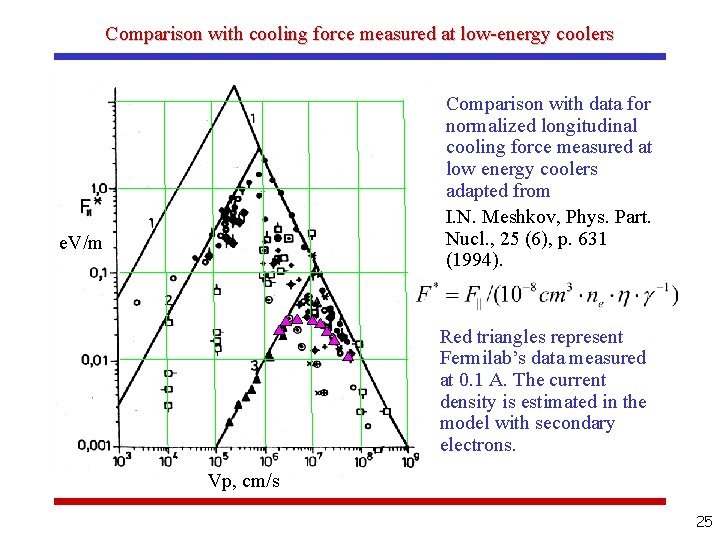
Comparison with cooling force measured at low-energy coolers Comparison with data for normalized longitudinal cooling force measured at low energy coolers adapted from I. N. Meshkov, Phys. Part. Nucl. , 25 (6), p. 631 (1994). e. V/m Red triangles represent Fermilab’s data measured at 0. 1 A. The current density is estimated in the model with secondary electrons. Vp, cm/s 25

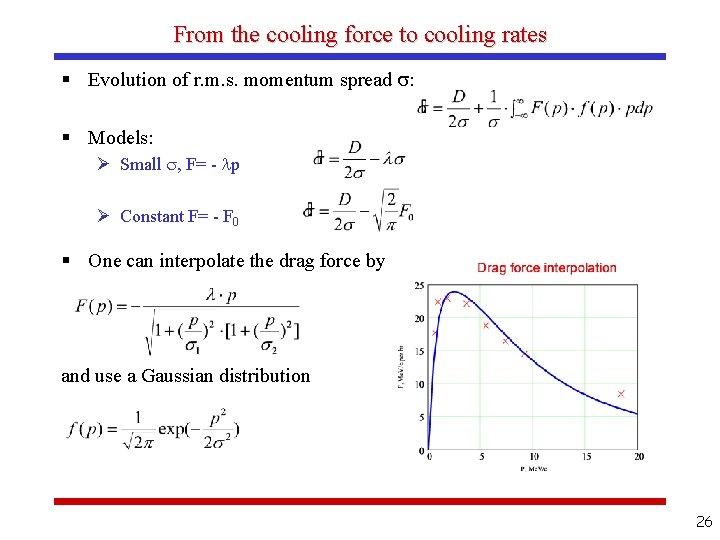
From the cooling force to cooling rates § Evolution of r. m. s. momentum spread : § Models: Ø Small , F= - p Ø Constant F= - F 0 § One can interpolate the drag force by and use a Gaussian distribution 26

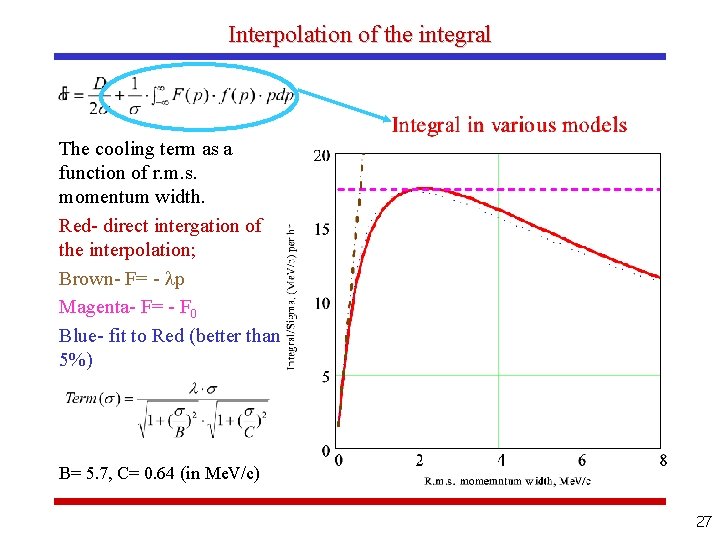
Interpolation of the integral The cooling term as a function of r. m. s. momentum width. Red- direct intergation of the interpolation; Brown- F= - p Magenta- F= - F 0 Blue- fit to Red (better than 5%) B= 5. 7, C= 0. 64 (in Me. V/c) 27

Diffusion by IBS § A. Burov’s approximation with Recycler numbers § Dimensions: Ø Ø Ø D – (Me. V/c)2/hr Np- in 1010 - mm mrad - sec - Me. V/c § Far from equilibrium, the term with the IBS diffusion is negligible. Ø At Np= 200, = 6, = 4 D/(2 )= 0. 7 Me. V/c per hour 28

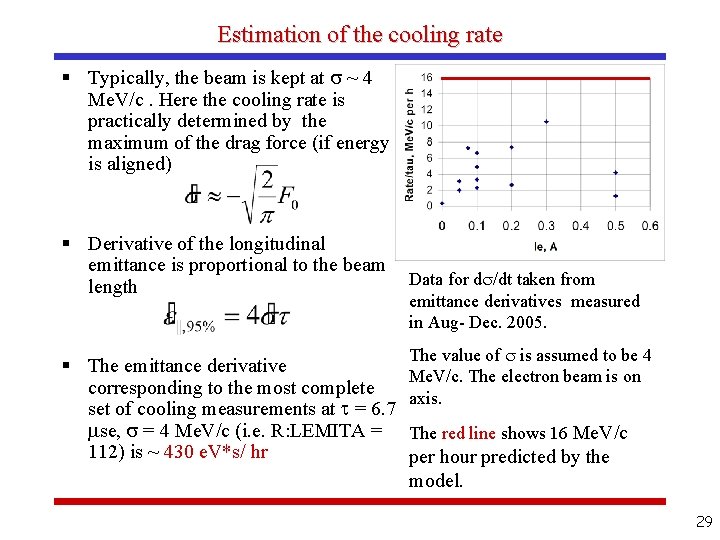
Estimation of the cooling rate § Typically, the beam is kept at ~ 4 Me. V/c. Here the cooling rate is practically determined by the maximum of the drag force (if energy is aligned) § Derivative of the longitudinal emittance is proportional to the beam length § The emittance derivative corresponding to the most complete set of cooling measurements at = 6. 7 se, = 4 Me. V/c (i. e. R: LEMITA = 112) is ~ 430 e. V*s/ hr Data for d /dt taken from emittance derivatives measured in Aug- Dec. 2005. The value of is assumed to be 4 Me. V/c. The electron beam is on axis. The red line shows 16 Me. V/c per hour predicted by the model. 29

Summary § The drag rate data fit satisfactorily to the simulated curve with three fitting parameters (current density, electron angles, and the energy spread). § The fitted parameters agree with the corresponding values estimated from measurements and simulations of the electron beam properties within ~ 50%. The main discrepancy is with fitting of the current density. The secondary electron model doesn’t alleviate the discrepancy. § The cooling rates are ~ 2 times lower than predicted from the drag rate measured on axis 30