Fitting Lines to Data with Outliers and Errors

Fitting Lines to Data with Outliers and Errors in the Variables Nahum Kiryati TAU © Copyrighted material. All rights reserved. Freddy Bruckstein Technion

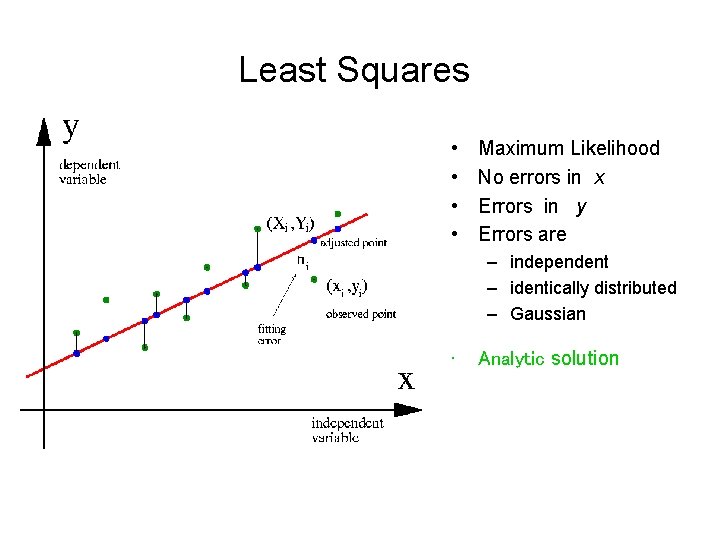
Least Squares • • Maximum Likelihood No errors in x Errors in y Errors are – independent – identically distributed – Gaussian • Analytic solution

From Maximum-Likelihood to Least-Squares (reminder) Maximum Likelihood: Independent Gaussian errors: log is a monotonic function: Identically distributed errors: . . . Least Squares

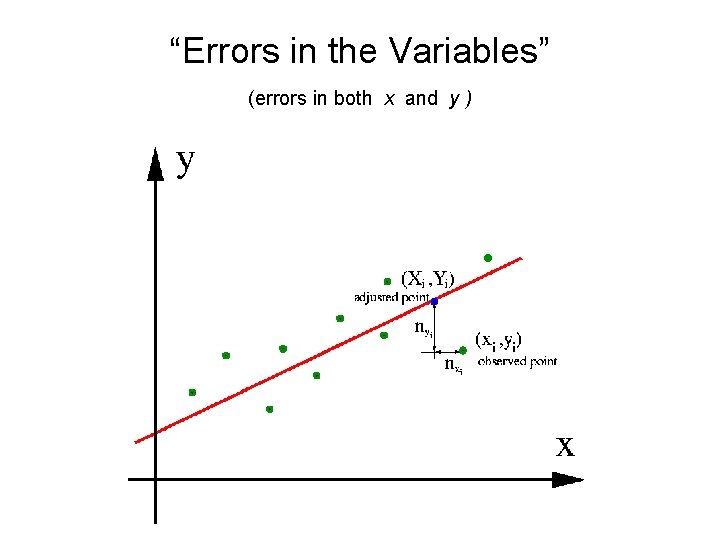
“Errors in the Variables” (errors in both x and y )

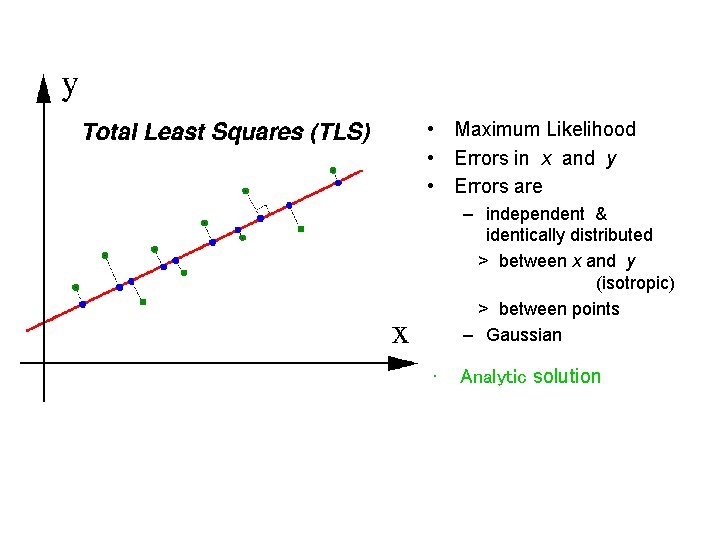
• Maximum Likelihood • Errors in x and y • Errors are – independent & identically distributed > between x and y (isotropic) > between points – Gaussian • Analytic solution

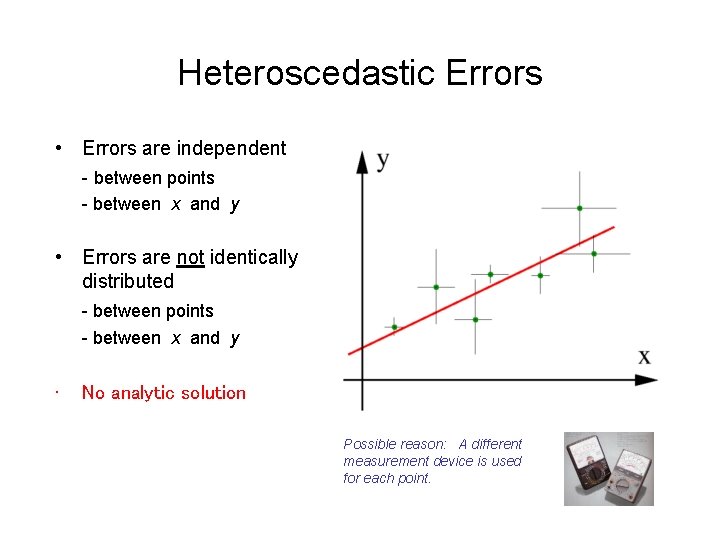
Heteroscedastic Errors • Errors are independent - between points - between x and y • Errors are not identically distributed - between points - between x and y • No analytic solution Possible reason: A different measurement device is used for each point.

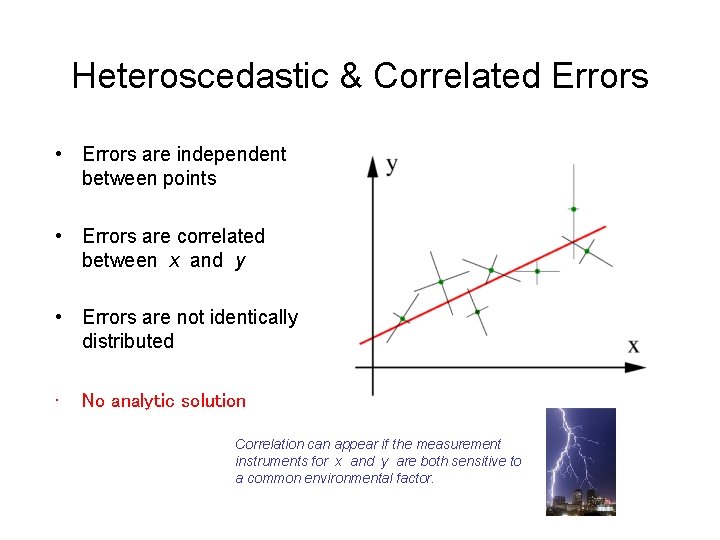
Heteroscedastic & Correlated Errors • Errors are independent between points • Errors are correlated between x and y • Errors are not identically distributed • No analytic solution Correlation can appear if the measurement instruments for x and y are both sensitive to a common environmental factor.

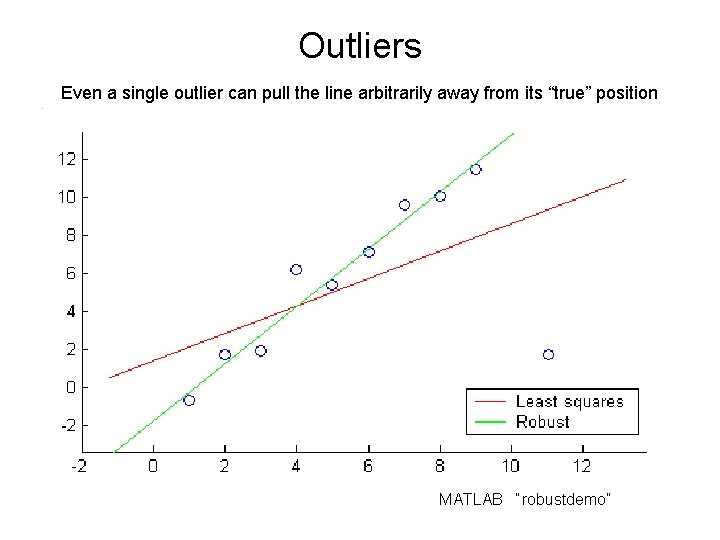
Outliers Even a single outlier can pull the line arbitrarily away from its “true” position MATLAB “robustdemo”

Robust Approaches • Least Median of Squares • Robust M-estimation • Reweighted Least-Squares • etc. . .

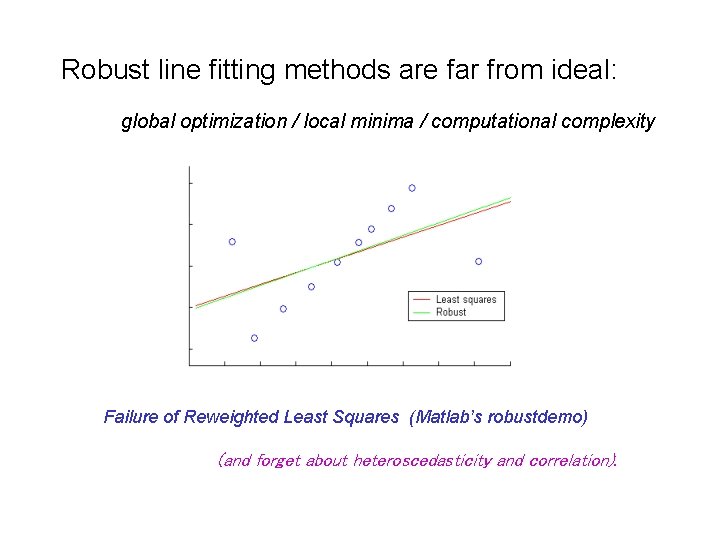
Robust line fitting methods are far from ideal: global optimization / local minima / computational complexity Failure of Reweighted Least Squares (Matlab’s robustdemo) (and forget about heteroscedasticity and correlation).

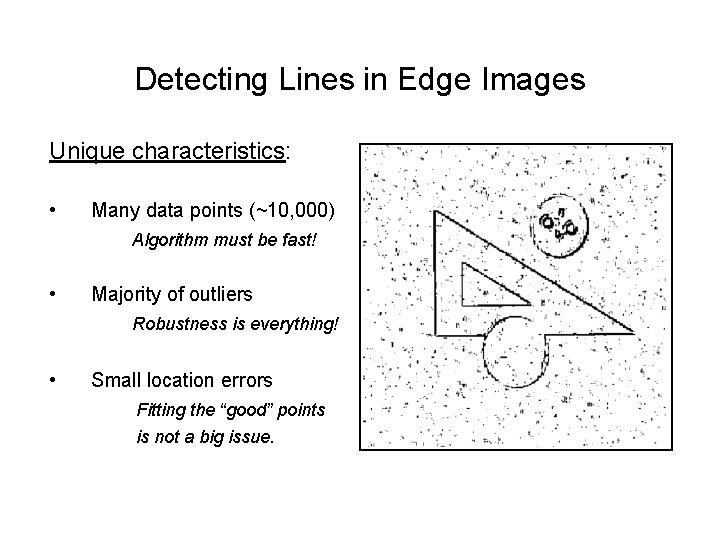
Detecting Lines in Edge Images Unique characteristics: • Many data points (~10, 000) Algorithm must be fast! • Majority of outliers Robustness is everything! • Small location errors Fitting the “good” points is not a big issue.

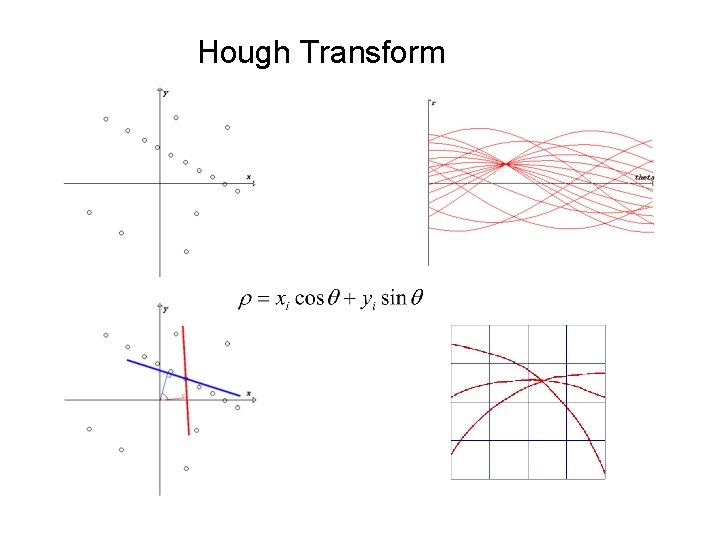
Hough Transform

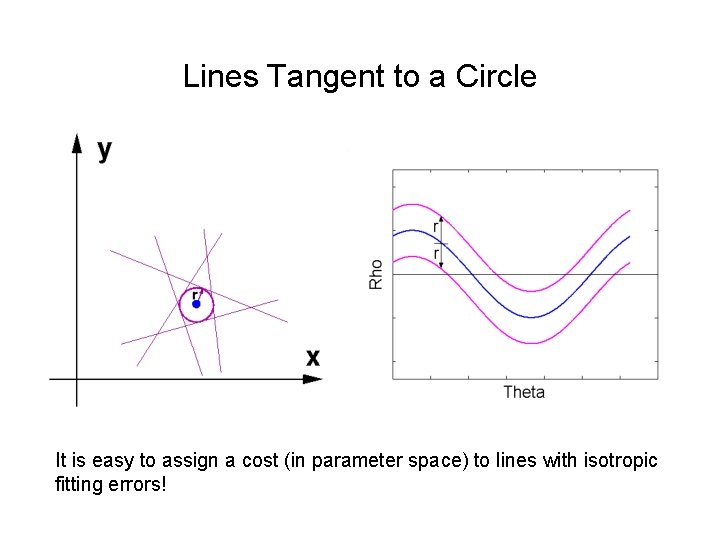
Lines Tangent to a Circle It is easy to assign a cost (in parameter space) to lines with isotropic fitting errors!

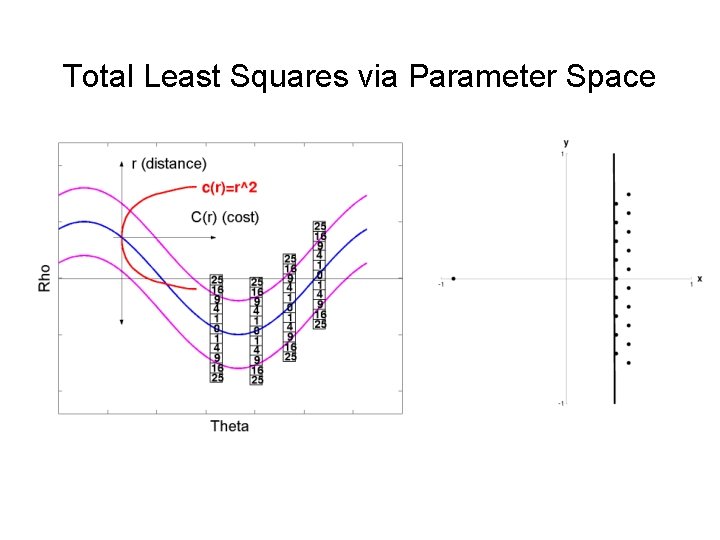
Total Least Squares via Parameter Space

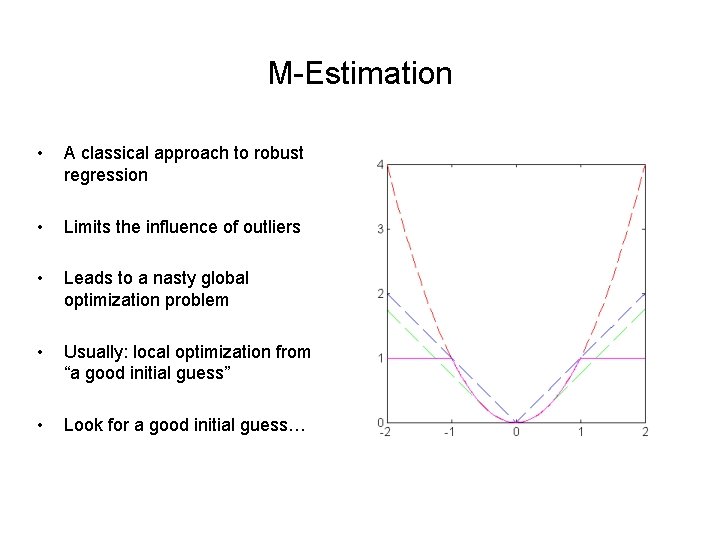
M-Estimation • A classical approach to robust regression • Limits the influence of outliers • Leads to a nasty global optimization problem • Usually: local optimization from “a good initial guess” • Look for a good initial guess…

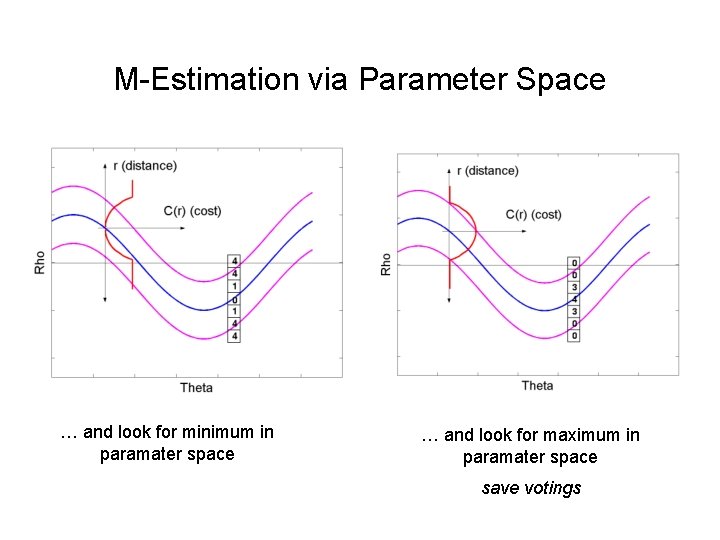
M-Estimation via Parameter Space … and look for minimum in paramater space … and look for maximum in paramater space save votings

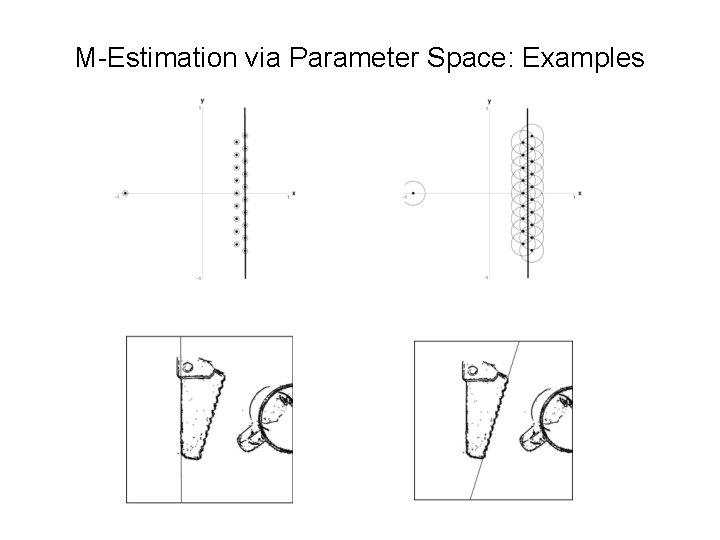
M-Estimation via Parameter Space: Examples

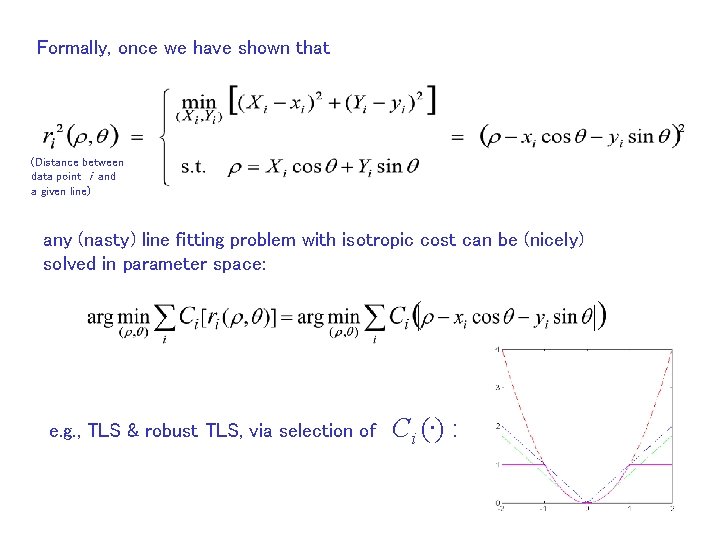
Formally, once we have shown that (Distance between data point i and a given line) any (nasty) line fitting problem with isotropic cost can be (nicely) solved in parameter space: e. g. , TLS & robust TLS, via selection of Ci (. ) :

Surprise! The (very ugly) correlated heteroscedastic case can also be beautified! (effective distance between data point i and a given line) Nominator: standard TLS term! Denominator: Rho-independent term!

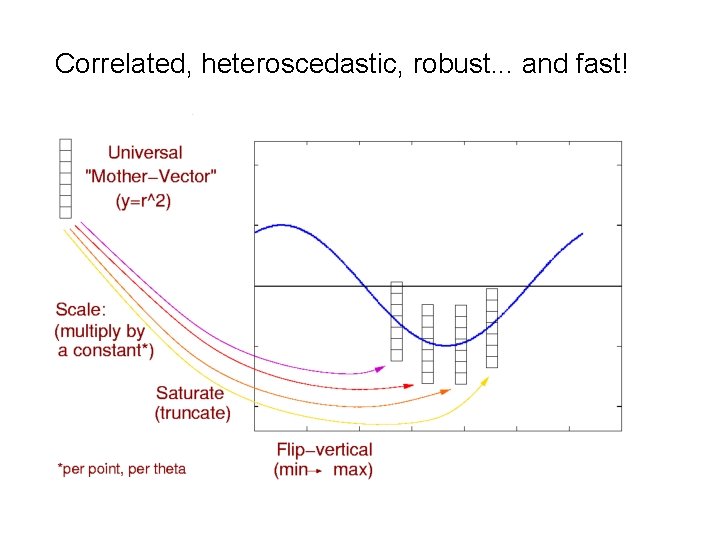
Correlated, heteroscedastic, robust. . . and fast!

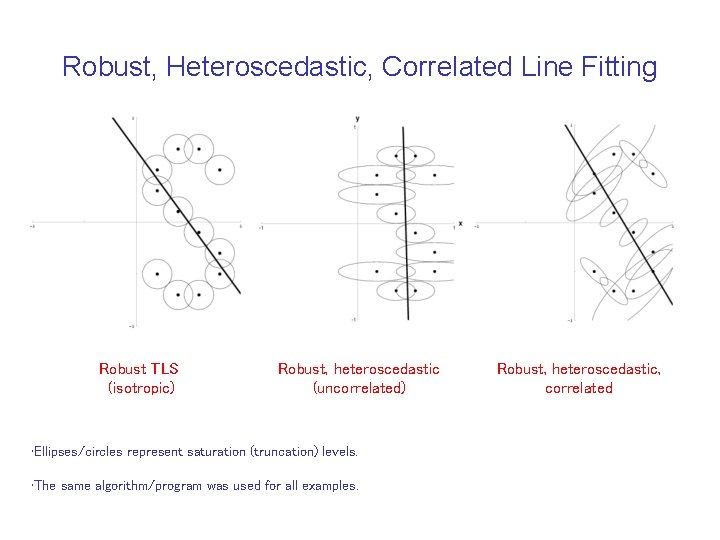
Robust, Heteroscedastic, Correlated Line Fitting Robust TLS (isotropic) Robust, heteroscedastic (uncorrelated) • Ellipses/circles represent saturation (truncation) levels. • The same algorithm/program was used for all examples. Robust, heteroscedastic, correlated

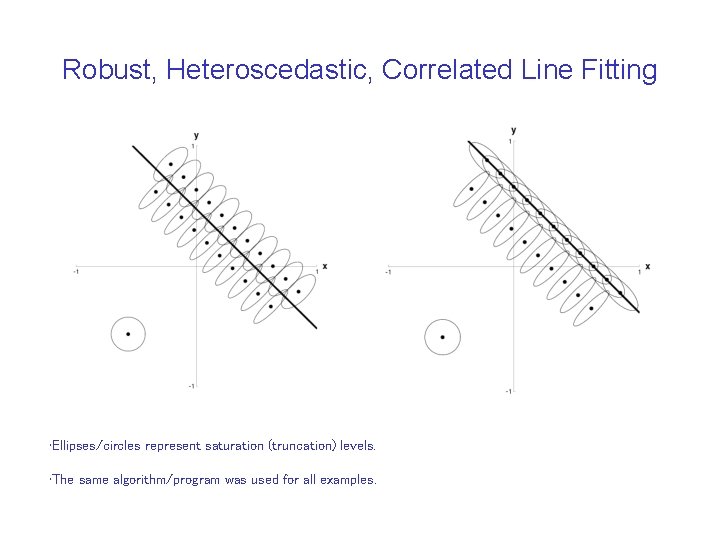
Robust, Heteroscedastic, Correlated Line Fitting • Ellipses/circles represent saturation (truncation) levels. • The same algorithm/program was used for all examples.

References N. Kiryati and A. M. Brucktein, “Heteroscedastic Hough Transform (Ht. HT): An Efficient Method for Robust line Fitting in the `Errors in the Variables’ Problem, Computer Vision and Image Understanding, Vol. 78, pp. 69 -83, 2000. N. Kiryati and A. M. Bruckstein, “What’s in a Set of Points? ”, IEEE Trans. Pattern Analysis Macine Intelligence, Vol. 14, pp. 496 -500, 1992. N. Kiryati and A. M. Bruckstein, “On Navigating between Friends and Foes”, IEEE Trans. Pattern Analysis Macine Intelligence, Vol. 13, pp. 602 -606, 1991.