Fitting Fitting Choose a parametric objectsome objects to

Fitting

Fitting • Choose a parametric object/some objects to represent a set of tokens • Most interesting case is when criterion is not local – can’t tell whether a set of points lies on a line by looking only at each point and the next. CS 8690 Computer Vision • Three main questions: – what object represents this set of tokens best? – which of several objects gets which token? – how many objects are there? (you could read line for object here, or circle, or ellipse or. . . ) University of Missouri at Columbia
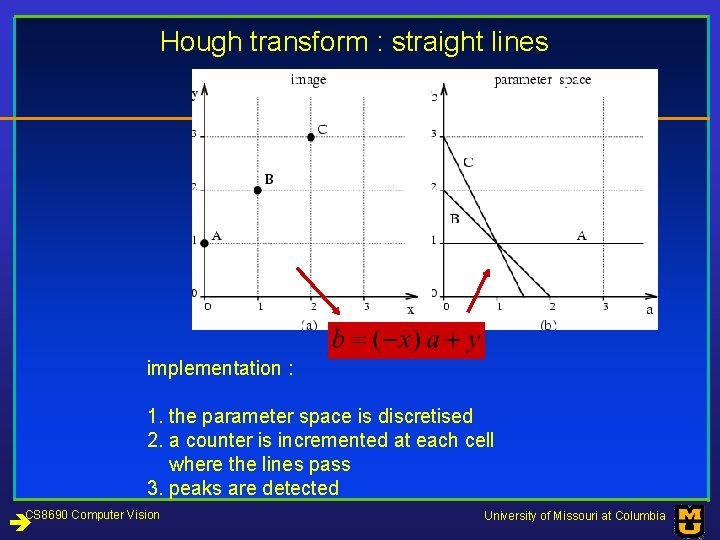
Hough transform : straight lines implementation : 1. the parameter space is discretised 2. a counter is incremented at each cell where the lines pass 3. peaks are detected CS 8690 Computer Vision University of Missouri at Columbia

Hough transform : straight lines problem : unbounded parameter domain vertical lines require infinite a alternative representation: Each point will add a cosine function in the ( , ) parameter space CS 8690 Computer Vision University of Missouri at Columbia
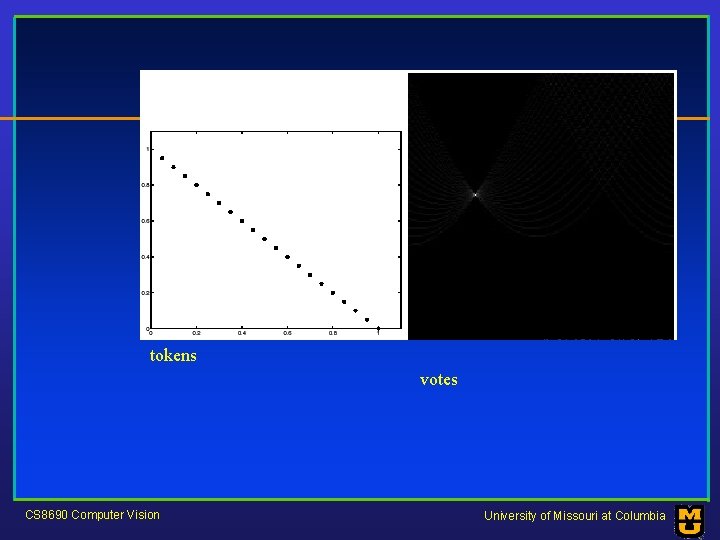
tokens votes CS 8690 Computer Vision University of Missouri at Columbia
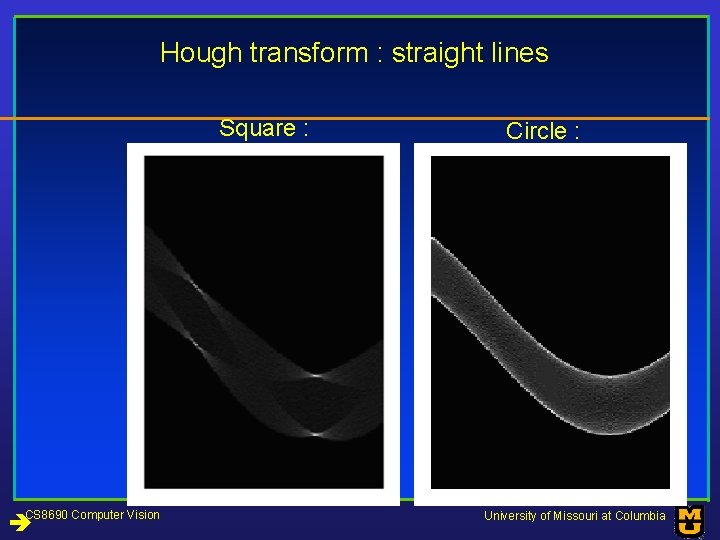
Hough transform : straight lines Square : CS 8690 Computer Vision Circle : University of Missouri at Columbia

Hough transform : straight lines CS 8690 Computer Vision University of Missouri at Columbia

Mechanics of the Hough transform • Construct an array representing , d • For each point, render the curve ( , d) into this array, adding one at each cell • Difficulties – how big should the cells be? (too big, and we cannot distinguish between quite different lines; too small, and noise causes lines to be missed) CS 8690 Computer Vision • How many lines? – count the peaks in the Hough array • Who belongs to which line? – tag the votes • Hardly ever satisfactory in practice, because problems with noise and cell size defeat it University of Missouri at Columbia
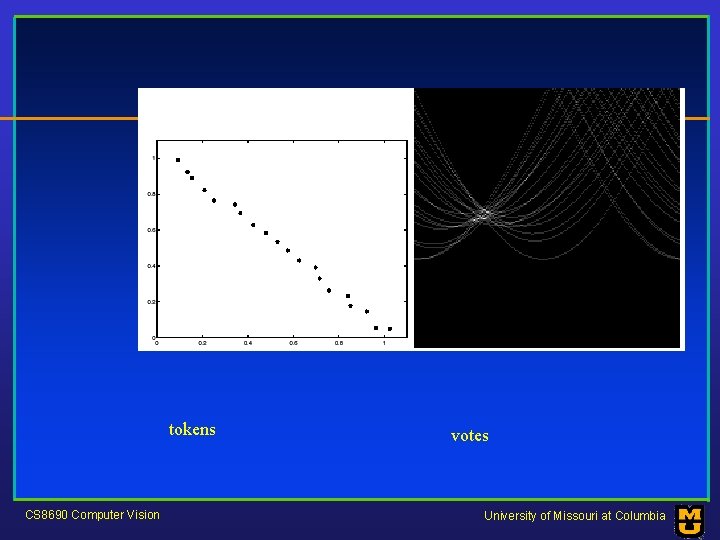
tokens CS 8690 Computer Vision votes University of Missouri at Columbia
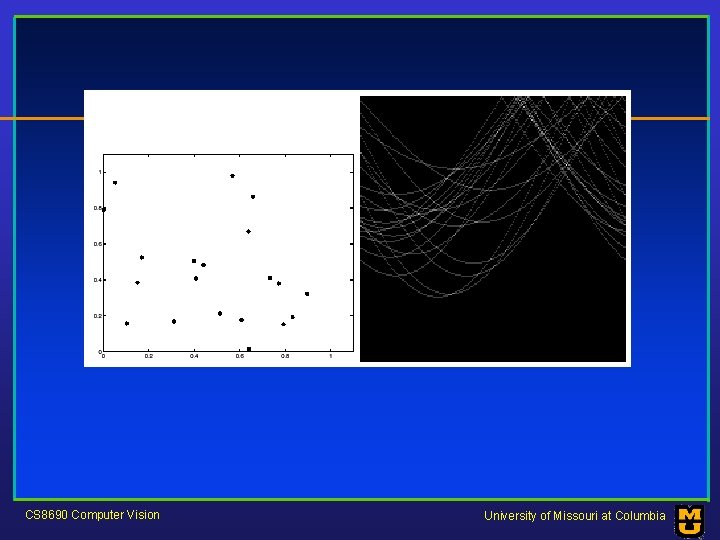
CS 8690 Computer Vision University of Missouri at Columbia
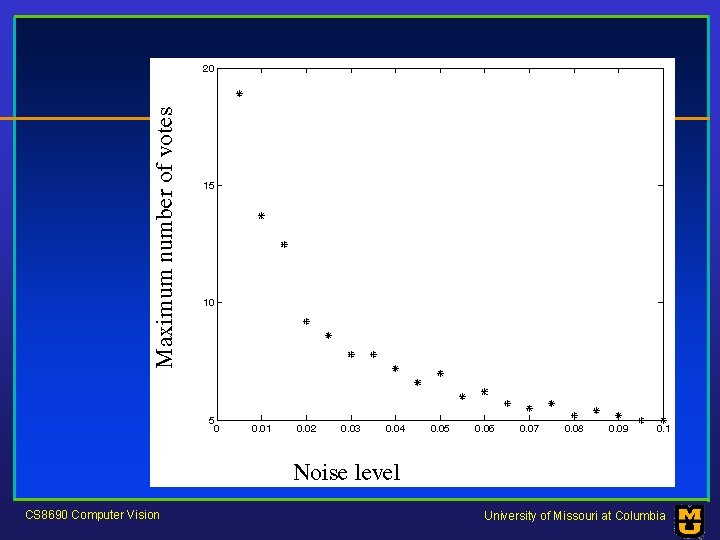
CS 8690 Computer Vision University of Missouri at Columbia

CS 8690 Computer Vision University of Missouri at Columbia

Hough Transform (Summary) • HT is a voting algorithm: each point votes for all combinations of parameters which may have produced it if it were part of the target curve. • The array of counters in parameter space can be regarded as a histogram. • The final total of votes c(m) in a counter of coordinate m indicates the relative likelihood of the hypothesis “a curve with parameter set m exists in the image”. CS 8690 Computer Vision University of Missouri at Columbia

Hough Transform (Summary) • HT can also be regarded as pattern matching: the class of curves identified by the parameter space is the class of patterns. • HT is more efficient than direct template matching which compares all possible appearances of the pattern with the image. CS 8690 Computer Vision University of Missouri at Columbia

Hough Transform Advantages • First all points are processed independently, it copes well with occlusion (if the noise does not result in peaks as high as those created by the shortest true lines). • Second it is relatively robust to noise, as spurious points are unlikely to contribute consistently to any single bin, just generate background noise. • Third, it detects multiple instances of a model in a single pass. CS 8690 Computer Vision University of Missouri at Columbia
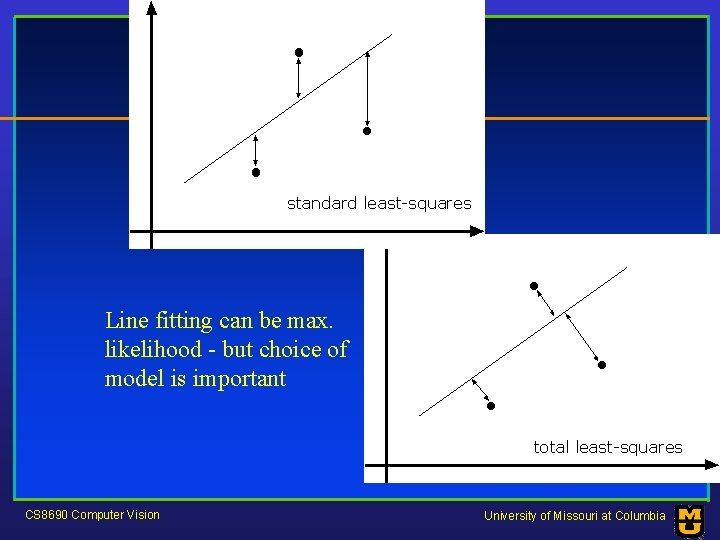
standard least-squares Line fitting can be max. likelihood - but choice of model is important total least-squares CS 8690 Computer Vision University of Missouri at Columbia

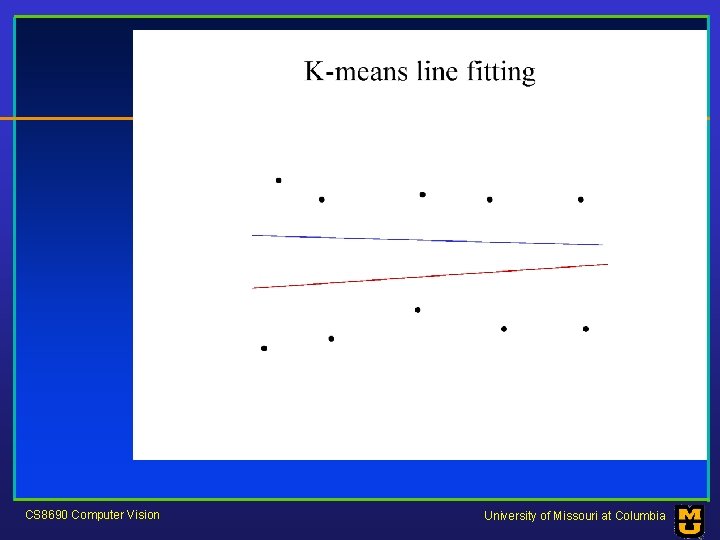
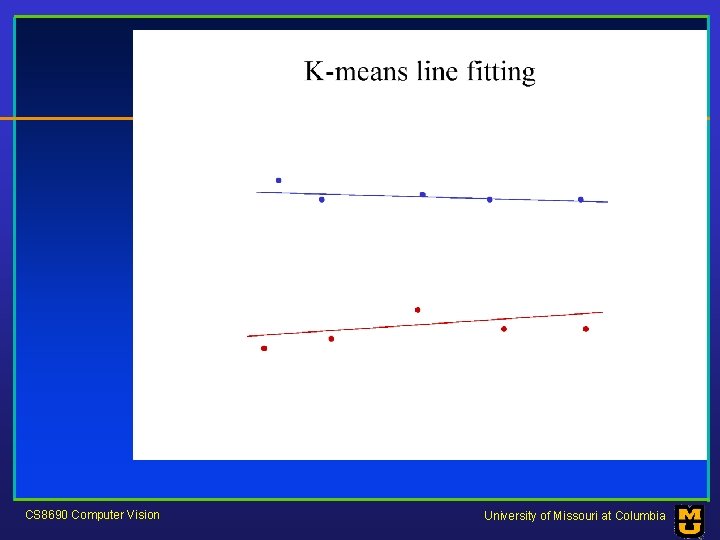
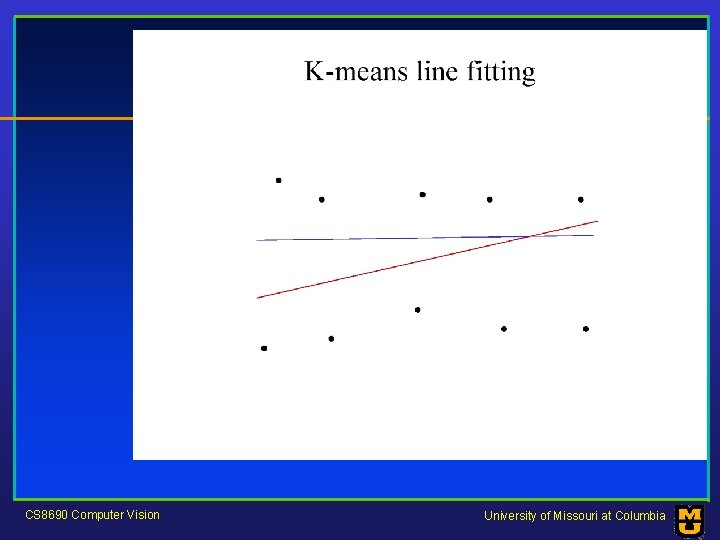
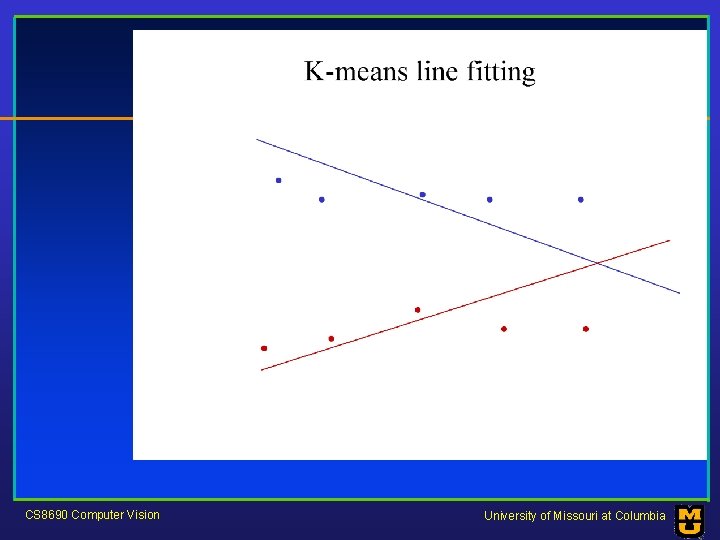
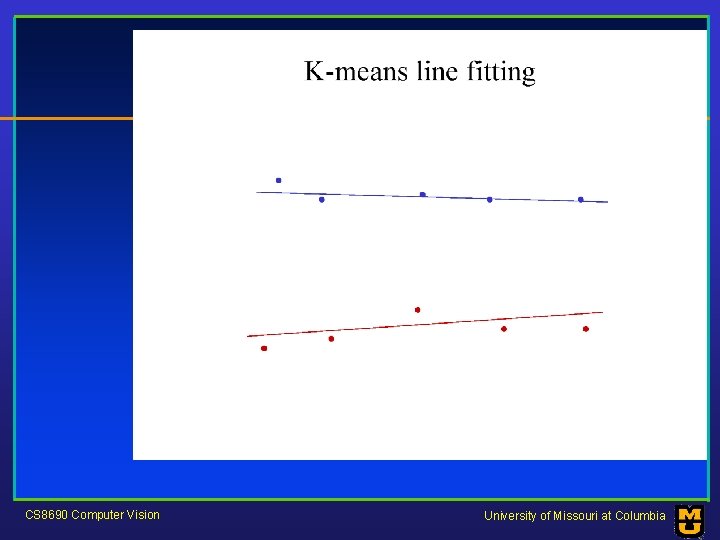
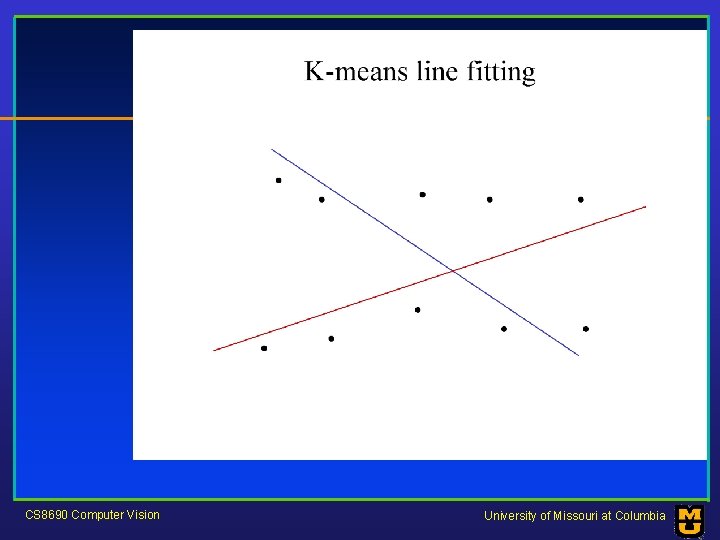
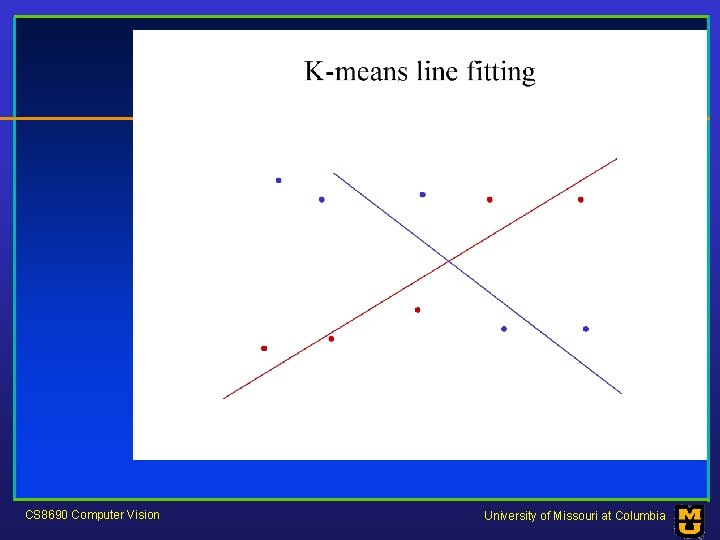
Who came from which line? • Assume we know how many lines there are - but which lines are they? – easy, if we know who came from which line • Three strategies – Incremental line fitting – K-means – Probabilistic (later!) CS 8690 Computer Vision University of Missouri at Columbia

CS 8690 Computer Vision University of Missouri at Columbia

CS 8690 Computer Vision University of Missouri at Columbia
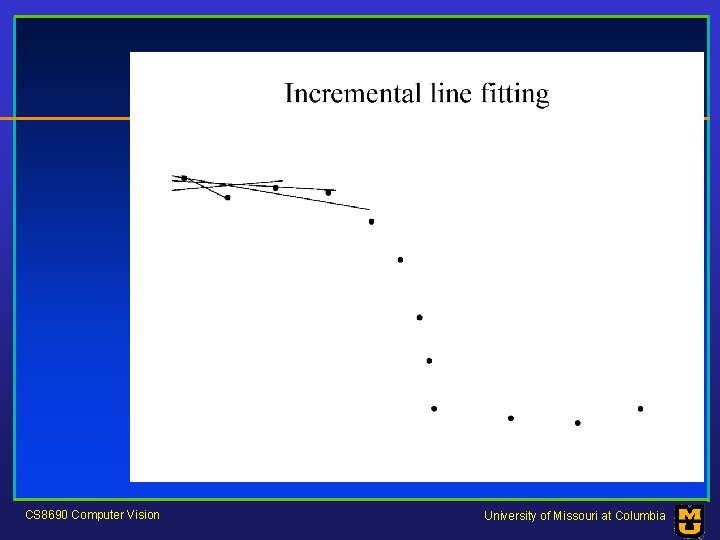
CS 8690 Computer Vision University of Missouri at Columbia
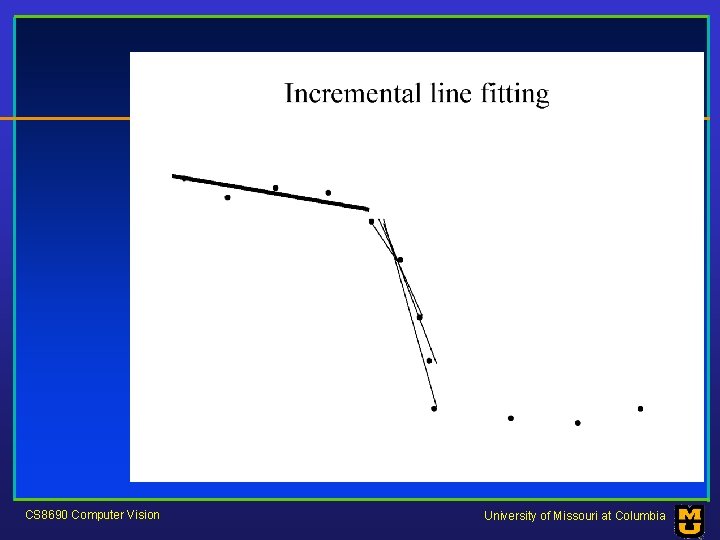
CS 8690 Computer Vision University of Missouri at Columbia
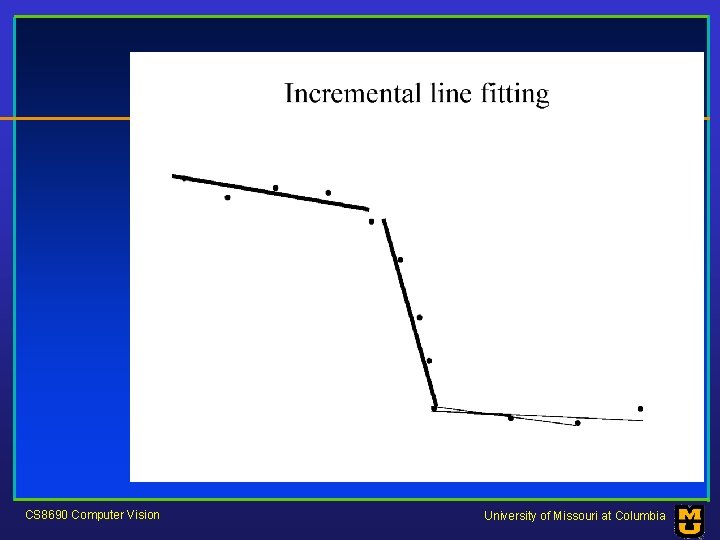
CS 8690 Computer Vision University of Missouri at Columbia
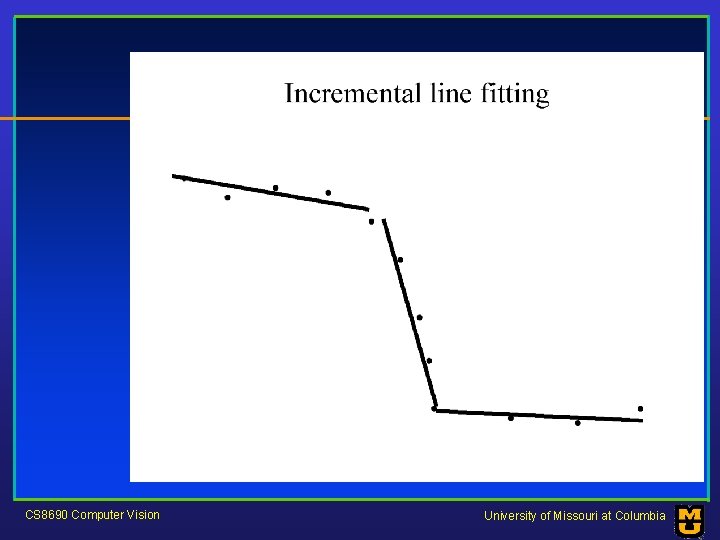
CS 8690 Computer Vision University of Missouri at Columbia

CS 8690 Computer Vision University of Missouri at Columbia
CS 8690 Computer Vision University of Missouri at Columbia
CS 8690 Computer Vision University of Missouri at Columbia
CS 8690 Computer Vision University of Missouri at Columbia
CS 8690 Computer Vision University of Missouri at Columbia
CS 8690 Computer Vision University of Missouri at Columbia
CS 8690 Computer Vision University of Missouri at Columbia
CS 8690 Computer Vision University of Missouri at Columbia

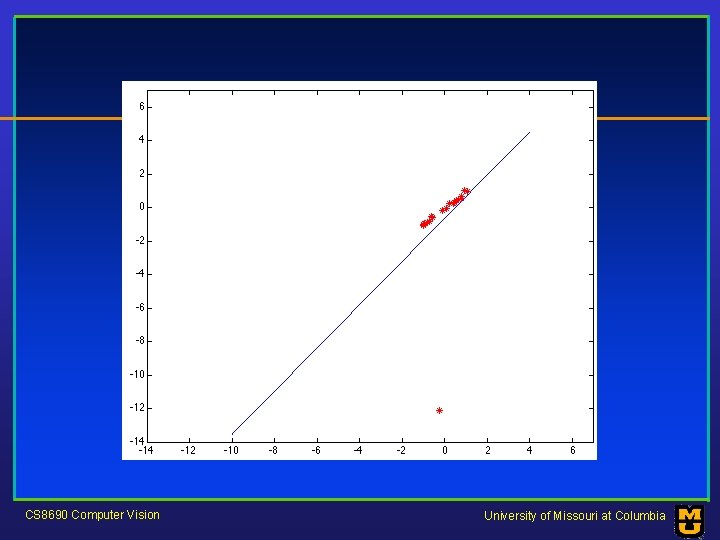
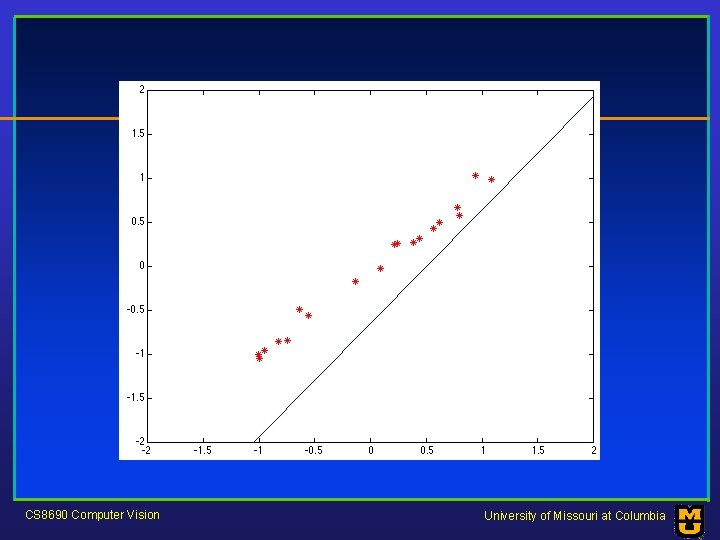
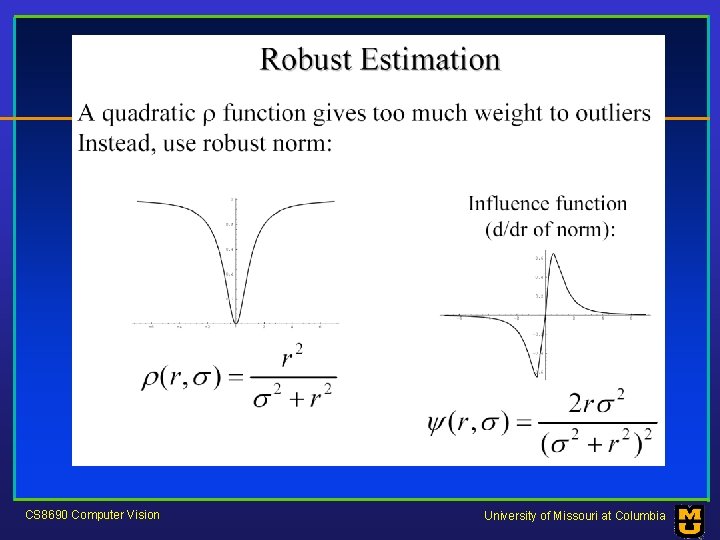
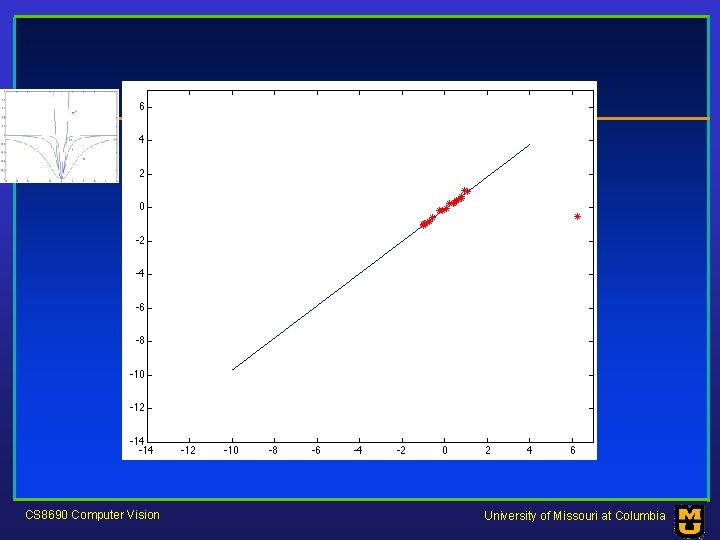
Robustness • As we have seen, squared error can be a source of bias in the presence of noise points – One fix is EM - we’ll do this shortly – Another is an M-estimator • Square nearby, threshold far away – A third is RANSAC • Search for good points CS 8690 Computer Vision University of Missouri at Columbia

CS 8690 Computer Vision University of Missouri at Columbia

CS 8690 Computer Vision University of Missouri at Columbia
CS 8690 Computer Vision University of Missouri at Columbia
CS 8690 Computer Vision University of Missouri at Columbia

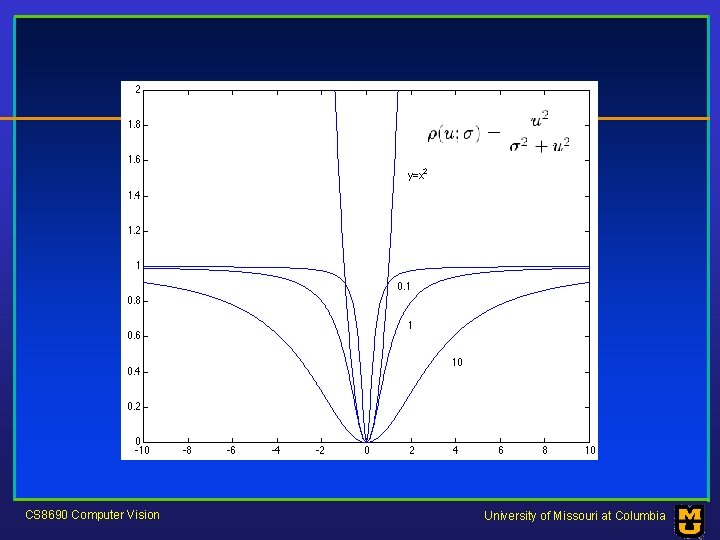
M-estimators • Generally, minimize where CS 8690 Computer Vision is the residual University of Missouri at Columbia
CS 8690 Computer Vision University of Missouri at Columbia
CS 8690 Computer Vision University of Missouri at Columbia
CS 8690 Computer Vision University of Missouri at Columbia

Too small CS 8690 Computer Vision University of Missouri at Columbia
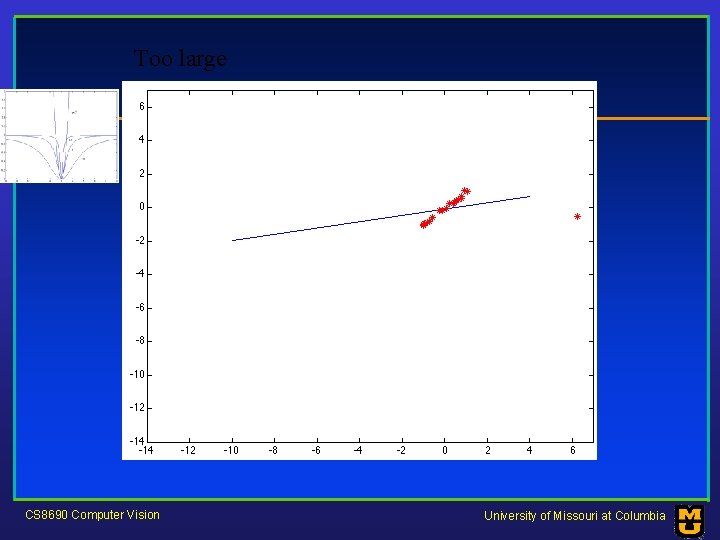
Too large CS 8690 Computer Vision University of Missouri at Columbia

CS 8690 Computer Vision University of Missouri at Columbia

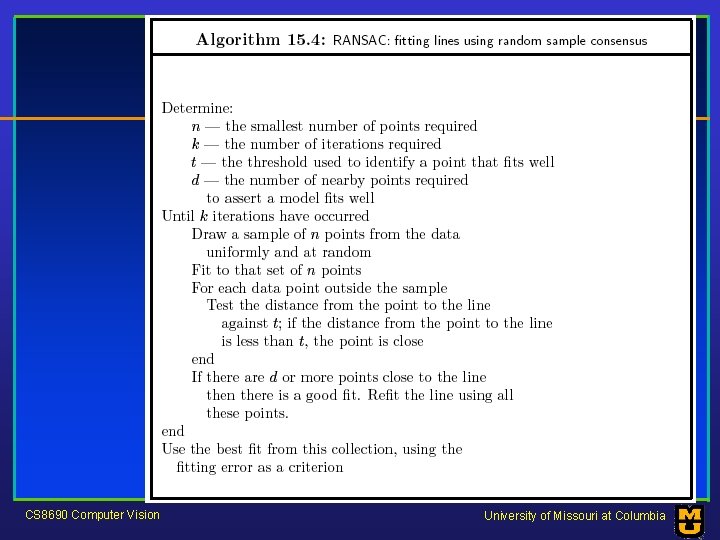
RANSAC • Choose a small subset uniformly at random • Fit to that • Anything that is close to result is signal; all others are noise • Refit • Do this many times and choose the best CS 8690 Computer Vision • Issues – How many times? • Often enough that we are likely to have a good line – How big a subset? • Smallest possible – What does close mean? • Depends on the problem – What is a good line? • One where the number of nearby points is so big it is unlikely to be all outliers University of Missouri at Columbia
CS 8690 Computer Vision University of Missouri at Columbia

Distance threshold Choose t so probability for inlier is α (e. g. 0. 95) • Often empirically • Zero-mean Gaussian noise σ then follows distribution with m=codimension of model (dimension+codimension=dimension space) CS 8690 Computer Vision Codimension Model t 2 1 line, F 3. 84σ2 2 H, P 5. 99σ2 3 T 7. 81σ2 University of Missouri at Columbia

How many samples? Choose N so that, with probability p, at least one random sample is free from outliers. e. g. p=0. 99 proportion of outliers e s 2 3 4 5 6 7 8 CS 8690 Computer Vision 5% 2 3 3 4 4 4 5 10% 3 4 5 6 7 8 9 20% 5 7 9 12 16 20 26 25% 30% 6 7 9 11 13 17 17 26 24 37 33 54 44 78 40% 50% 11 17 19 35 34 72 57 146 97 293 163 588 272 1177 University of Missouri at Columbia

Acceptable consensus set? • Typically, terminate when inlier ratio reaches expected ratio of inliers CS 8690 Computer Vision University of Missouri at Columbia

Fitting curves other than lines • In principle, an easy generalisation – The probability of obtaining a point, given a curve, is given by a negative exponential of distance squared CS 8690 Computer Vision • In practice, rather hard – It is generally difficult to compute the distance between a point and a curve University of Missouri at Columbia
- Slides: 49