FIRST QUESTIONS FOR ALGORITHM ANALYSIS WHAT IS AN

FIRST QUESTIONS FOR ALGORITHM ANALYSIS

WHAT IS AN ALGORITHM? From the text (p. 3): “An algorithm is a sequence of unambiguous instructions for solving a problem, i. e. , for obtaining a required output for any legitimate input in a finite amount of time. ” 9/9/2021 2 From the preceding line: “Although there is no universally agreed-on wording to describe this notion, there is general agreement about what the concept means: ”

PROBLEMS WITH THE WORDING What do you see as problematic? ? ? Some might include: • Unambiguous • Instructions • Solving • Problem • Finite time Is this the only discipline with difficult primitives? 9/9/2021 3 • Geometry: Point, line, and plane; axioms (Euclid, Riemann, others) • Set Theory: Set

YET ANOTHER PERSPECTIVE Set and its members Set operations: • union, • intersection, • complement, (problem of having universe) • cross product of two sets Relation Function 9/9/2021 4 • Special type of relation • Sometimes expressed by a “rule” of relationship Could algorithms simply be functions?

COMPARE ALGORITHMS AND FUNCTIONS Sequentiality Lack of ambiguity Instructions Solving Problem Input – Output relationship Finiteness of time Uniqueness of expression 9/9/2021 5 Computation

SOME COMMON PROBLEMS ? ? ? Sorting • What does it mean formally? Searching String processing • Matching • Translation Graph • TSP • Connectedness Combinatorial • Optimization: TSP, QAP • Constraint satisfaction: SAT, Queen Placement, Knight’s Tour Geometric • Path planning Numerical (CSC 340) 9/9/2021 6 Etc.

DESCRIBING ALGORITHMIC BEHAVIOR Strategic • Greedy • Brute force • Enumeration (exhaustive) • Graph • DFS, BFS • Connectedness, planarity, etc. • Divide and conquer • Dynamic programming • Backtracking • Branch and bound • Recursive • Domain transformation Operational • Deterministic versus randomized • Exact (find an optimum or find a compliant) • Approximate (estimate pi) • Heuristic (choose quickly, WTA) Efficiency 9/9/2021 7 • Space • Time http: //en. wikipedia. org/wiki/List_of_algorithms

MEASUREMENT UNITS Space 9/9/2021 8 • Input magnitude (the number of bits needed to represent the input • Number of inputs • Space required to store the inputs, perform intermediate computations, and store outputs Time

9/9/2021 9 BIG O(. )

9/9/2021 10 FIND ALGORITHMS THAT ARE O(F(N))

9/9/2021 11 DO THINGS EVER GET WORSE?

9/9/2021 12 OTHER BOUNDS

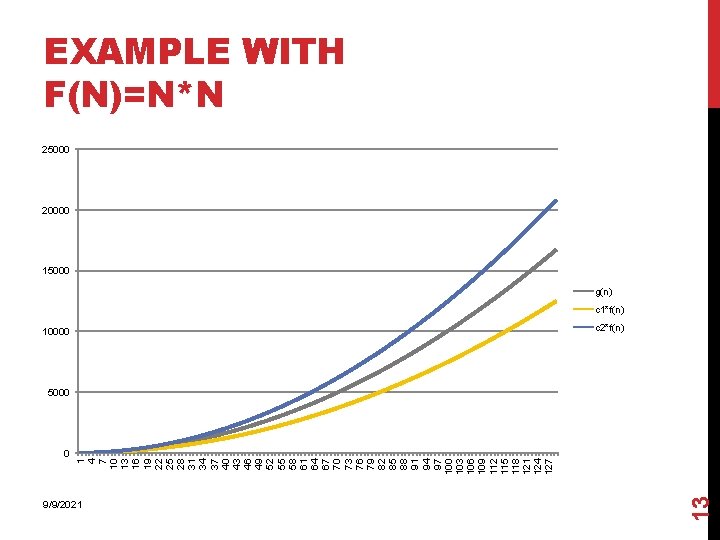
10000 9/9/2021 13 0 1 4 7 10 13 16 19 22 25 28 31 34 37 40 43 46 49 52 55 58 61 64 67 70 73 76 79 82 85 88 91 94 97 100 103 106 109 112 115 118 121 124 127 EXAMPLE WITH F(N)=N*N 25000 20000 15000 g(n) c 1*f(n) c 2*f(n) 5000

ANALYZING NONRECURSIVE ALGORITHMS How should input size be measured? • Number of items in a list • Value of a parameter or the number of bits needed to store the parameter What is the program’s most frequently occurring operation? • Look inside loops Are there other factors than input size that affect the frequency of the most frequent operation? • Separate best, worst and average case analyses How to tally the frequency? 9/9/2021 14 • Summations • Profiling

EXAMPLE 1 Find max Given a list containing n>0 integers (It is a separate question to ask the time for set-up. What would it be for this example? ) Pseudo-code max = list[0] for i = 0 to n-1 if list[i]>max = list[i] 9/9/2021 15 Analysis?

EXAMPLE 1 ANALYSIS max = list[0] • O(1) = load + store if… • Evaluate condition (a difference) • Conditional transfer (a jump, branch or skip depending upon flag values) • Assignment = load + store • O(? ? ) for… 9/9/2021 16 • Iterates n times • Total accumulated time = ?

ANALYZING RECURSIVE ALGORITHMS To understand recursion one must first understand recursion Questions 9/9/2021 17 • How will one measure input size? • What is the core operation? • Do other factors than input size influence the number of repetitions? • What is a recurrence expressing the repetition of the core operation? • Solve the recurrence?

EXAMPLE 2: A RECURSIVE ALGORITHM import random import math c = [0, 0] alist=[] n = int(input('Number of items for list = ' )) for i in range(n): x = random. randint(1, 1000) alist. append(x) ##print(len(alist)) ##print('The initial list = ', alist) def recursfindmax(alis): print(alis) def findmax(alis): amax = alis[0] for i in range(len(alis)): c[1]+=1 if amax < alis[i]: amax = alis[i] return (amax) print('Recursive max = ', recursfindmax(alist)) print('Iterative max = ', findmax(alist)) print('Count recursive, iterative ', c) if len(alis) == 1: c[0]+=1 return alis[0] else: 9/9/2021 amax = max(alis[0], recursfindmax(alis[1: len(alis)])) return(amax) 18 c[0]+=1

ANALYSIS t(n) = 1 + t(n-1) = 1 + t(n-2) = 1 + t(n-3) = 1 + t(n-4) … t(n-(n-2)) = 1 + t(n-(n-1)) = t(1) = 1; this is the anchor 9/9/2021 19 t(n) = 1 + t(n-1) = 2 + t(n-2) = 3 + t(n-3) = … = (n-1) + t(n-(n-1)) =n

COMPARISON Both methods are O(n), where n is the number of items in the list 9/9/2021 20 How do the algorithms compare with respect to space utilization?

9/9/2021 21 FUN FACT

9/9/2021 22 FUN FACT (CONT’D)

9/9/2021 23 CONSIDER THE FIBONACCI NUMBER RECURRENCE

9/9/2021 24 SOLVING THE EQUATION

9/9/2021 25 APPLYING INITIAL CONDITIONS

9/9/2021 26 NOTES

COUNTING ADDITIONS IN RECURSIVE FIBONACCI A(n) = 1 (addition)+1 A(n-1)+ 1 A(n-2) =1 + 1 +A(n-2)+A(n-3)+ A(n-2) = 2 + 2 A(n-2) + 1 A(n-3) = 2 + 2(1+A(n-3)+A(n-4))+A(n-3) = 4 + 3 A(n-3) + 2 A(n-4) = 4 + 3(1+A(n-4)+A(n-5))+2 A(n-4) = 7 + 5 A(n-4)+3 A(n-5) = 7 + 5(1 + A((n-5)+A(n-6))+ 3 A(n-5) = 12 + 8 A(n-5) + 5 A(n-6) =… = (Fib(i+2) -1)+Fib(i+1)A(n-i)+Fib(i)A(n-(i+1)) 9/9/2021 27 Letting i = n-1, yields A(n) = Fib(n+1)-1, since A(0)=A(1)=0

EMPIRICAL VERFICIATION c=[0, 0, 0] def fib(n): c[0]+=1 if n>1: c[1]+=1 return fib(n-1)+fib(n-2) elif n==0: c[2]+=1 return 0 else: c[3]+=1 return 1 c[4]+=1 print(fib(int(input("Supply a number: ")))) 9/9/2021 28 print(c)