First Order Logic First Order Logic AKAPredicate Calculus

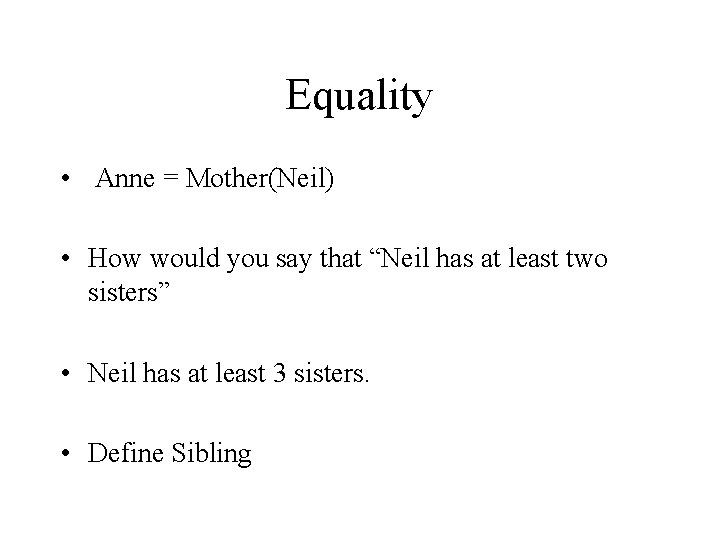
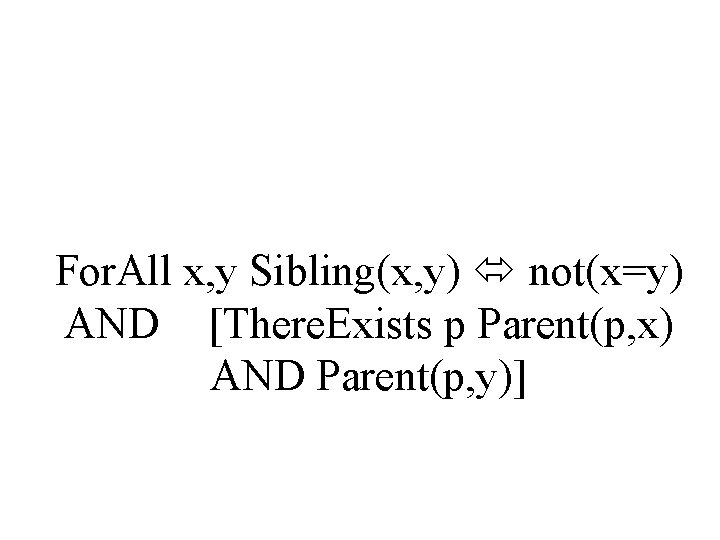
  • Slides: 23
Download presentation
First Order Logic

First Order Logic

First Order Logic (AKA-Predicate Calculus) vs (Propositional Logic) • Propositional Logic we talk about

First Order Logic (AKA-Predicate Calculus) vs (Propositional Logic) • Propositional Logic we talk about atomic facts – Propositional logic has no objects. – Because it has no objects it also has no relationships between objects, or functions that names objects • FOL- Stronger ontological commitment – Objects (with individual identities) – Objects have properties – Relations between objects • FOL is very well understood

First Order Logic Syntax For. All | There. Exists

First Order Logic Syntax For. All | There. Exists

First order logic has • SENTENCES that represent Boolean facts • TERMS which represent

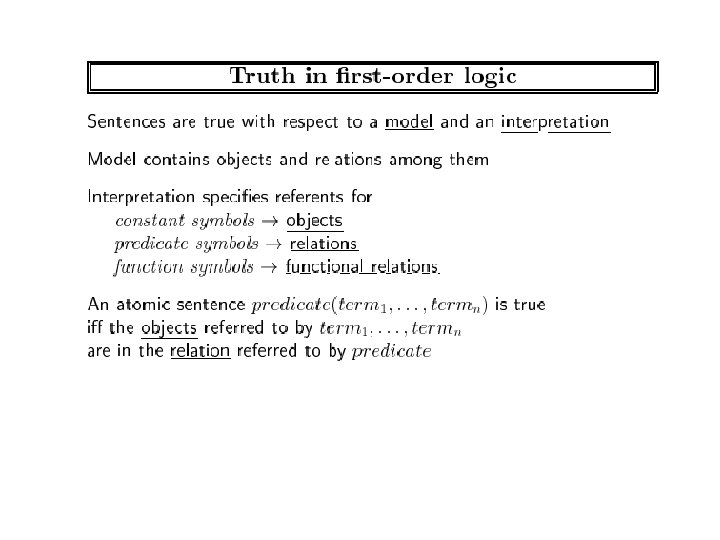
First order logic has • SENTENCES that represent Boolean facts • TERMS which represent objects • CONSTANTS and VARIABLES which represent objects • PREDICATE which given an object (I. e. TERM) it returns true or false • FUNCTIONS which given an object will return another object

Details – Informally: Objects like Colin. Powell, Mars, Austrailia – Variables: general use lower

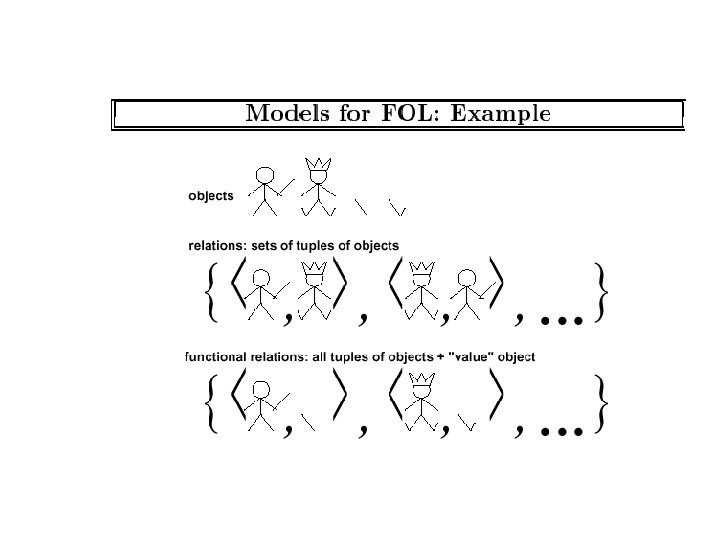
Details – Informally: Objects like Colin. Powell, Mars, Austrailia – Variables: general use lower case letters – Constants: Use uppercase, or starting with uppercase – Formally Speaking a predicate is a set of tuples • Brother. Hood. Predicate={<King. John, Richard. The. Lion. Heart> < Richard. The. Lion. Heart, King. John> }

Atomic Sentence – Brother(Richard, John) – Married(Father. Of(Richard), Mother. Of(John)) – An atomic sentence

Atomic Sentence – Brother(Richard, John) – Married(Father. Of(Richard), Mother. Of(John)) – An atomic sentence is true iff the relation referred to by the predicate holds between the objects referred to by the arguments

Complex Sentences • • • And, OR, Implies and Not Mother(Anne, Neil) ^ Mother(Anne,

Complex Sentences • • • And, OR, Implies and Not Mother(Anne, Neil) ^ Mother(Anne, Eileen) At. War(USA) v At. Peace(USA) Mother(Anne, Neil) Older(Anne, Neil) ¬Mother(Anne, George. Bush)

Universal Quantification • <variables> <sentence> • All students at WPI are smart. • s

Universal Quantification • <variables> <sentence> • All students at WPI are smart. • s at(s, WPI)=> smart(s) • What does this mean? • s at(s, WPI) ^ smart(s) All objects are at WPI and all objects are smart

Existential Quantification • <variables> <sentence> • There exist a student at MIT that is

Existential Quantification • <variables> <sentence> • There exist a student at MIT that is smart • s at(s, MIT) ^ smart(s) • What does this mean? • s at(s, MIT) => smart(s) If there is an object that is not at MIT then this

Formally Speaking

Formally Speaking

Equality • Anne = Mother(Neil) • How would you say that “Neil has at

Equality • Anne = Mother(Neil) • How would you say that “Neil has at least two sisters” • Neil has at least 3 sisters. • Define Sibling

For. All x, y Sibling(x, y) not(x=y) AND [There. Exists p Parent(p, x) AND

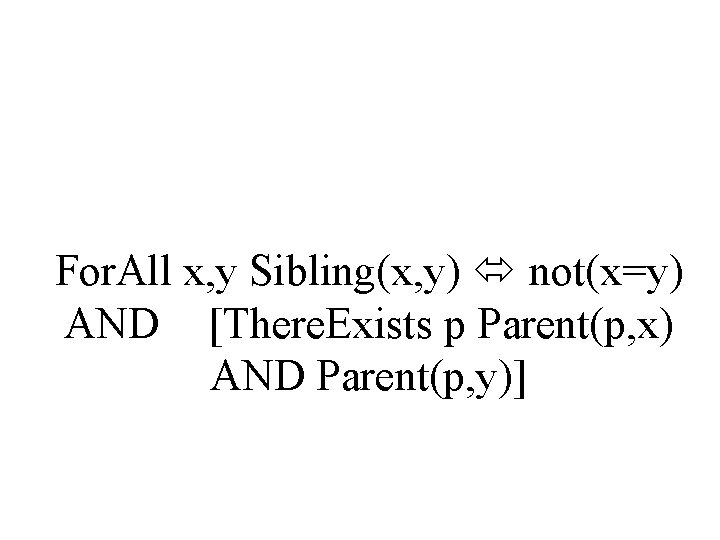
For. All x, y Sibling(x, y) not(x=y) AND [There. Exists p Parent(p, x) AND Parent(p, y)]

Formally Speaking about Equality • Equality is the identify relation – { <Neil, Neil>

Formally Speaking about Equality • Equality is the identify relation – { <Neil, Neil> <Tom, Tom> <grape 1, grape 1> …>

Practice – Squares neighboring the Wumpus are smelly – For. All s 1, s

Practice – Squares neighboring the Wumpus are smelly – For. All s 1, s 2 at(s 1, Wumpus) ^ neighbor(s 1, s 2)=>smelly(s 2)

Practice with the Kinship Domain • Sibling • For. All x, y Sibling(x, y)

Practice with the Kinship Domain • Sibling • For. All x, y Sibling(x, y) not(x=y) AND [There. Exists p Parent(p, x) AND Parent(p, y)] • Assume we have those on Page 198 • Define – – – Brother(x, y) Sister(x, y) Aunt(a, c) Brother. In. Law(b, x) Grandchild Great. Grand. Parent