First Order Circuit Capacitors and inductors RC and

First Order Circuit • Capacitors and inductors • RC and RL circuits

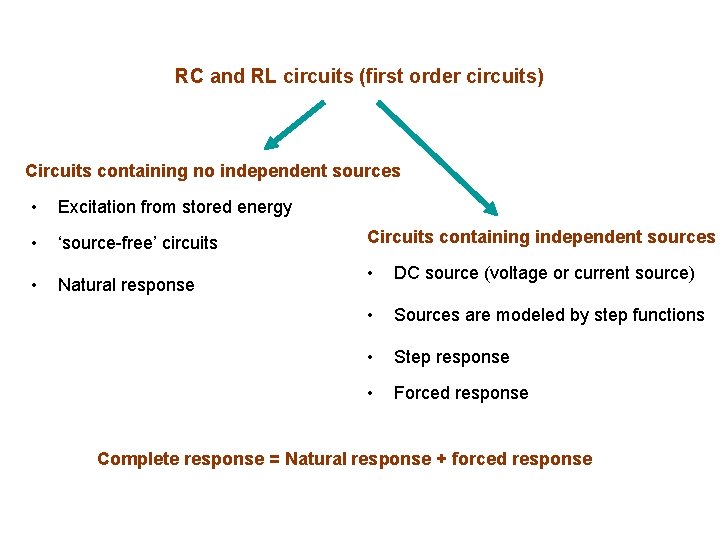
RC and RL circuits (first order circuits) Circuits containing no independent sources • Excitation from stored energy • ‘source-free’ circuits • Natural response Circuits containing independent sources • DC source (voltage or current source) • Sources are modeled by step functions • Step response • Forced response Complete response = Natural response + forced response

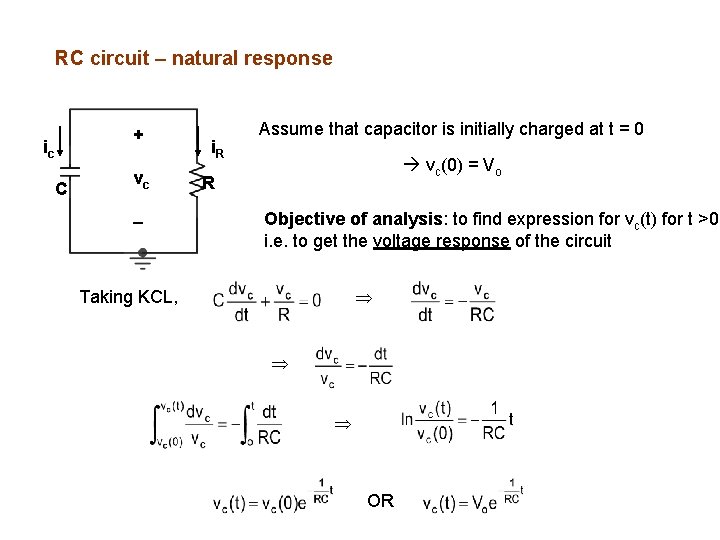
RC circuit – natural response + ic C vc i. R Assume that capacitor is initially charged at t = 0 vc(0) = Vo R Objective of analysis: to find expression for vc(t) for t >0 i. e. to get the voltage response of the circuit Taking KCL, OR

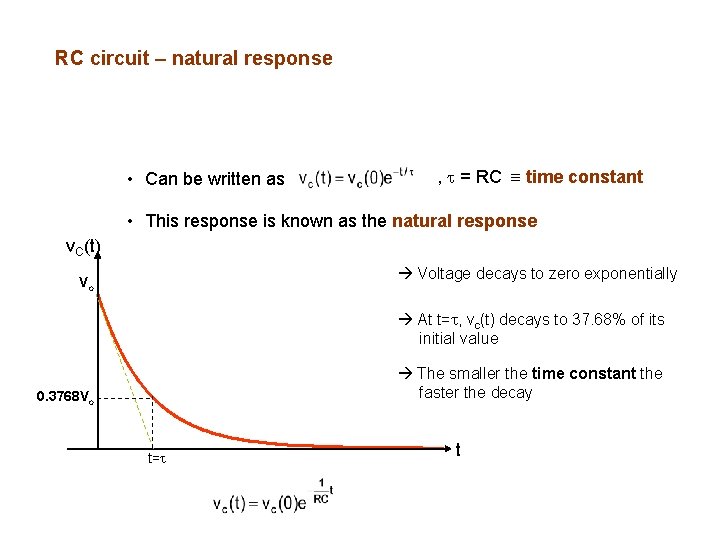
RC circuit – natural response • Can be written as , = RC time constant • This response is known as the natural response v. C(t) Voltage decays to zero exponentially Vo At t= , vc(t) decays to 37. 68% of its initial value The smaller the time constant the faster the decay 0. 3768 Vo t= t

RC circuit – natural response The capacitor current is given by: And the current through the resistor is given by The power absorbed by the resistor can be calculated as: The energy loss (as heat) in the resistor from 0 to t:

RC circuit – natural response As t , ER As t , energy initially stored in capacitor will be dissipated in the resistor in the form of heat

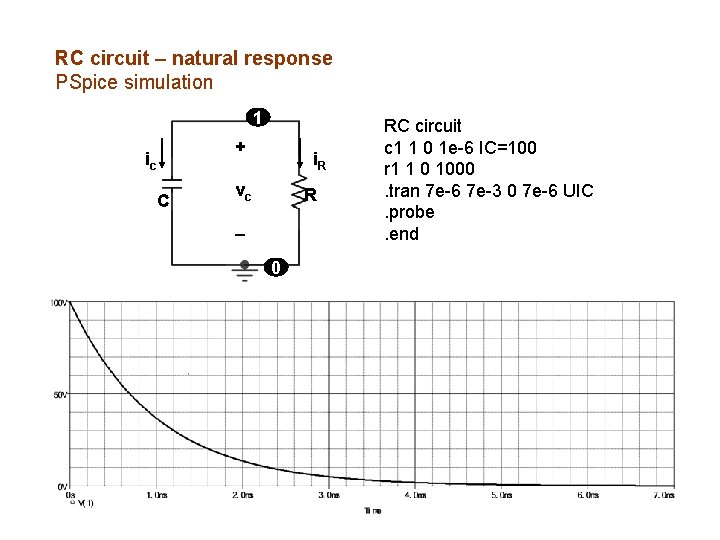
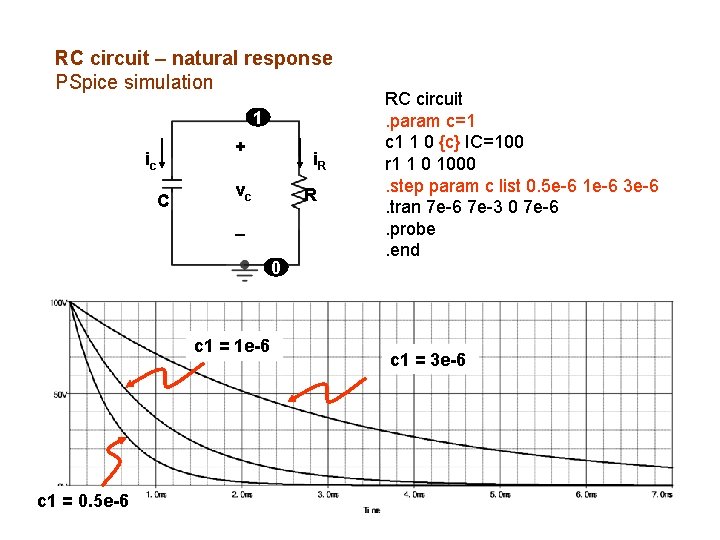
RC circuit – natural response PSpice simulation 1 + ic C i. R vc R 0 RC circuit c 1 1 0 1 e-6 IC=100 r 1 1 0 1000. tran 7 e-6 7 e-3 0 7 e-6 UIC. probe. end

RC circuit – natural response PSpice simulation 1 + ic C i. R vc R 0 c 1 = 1 e-6 c 1 = 0. 5 e-6 RC circuit. param c=1 c 1 1 0 {c} IC=100 r 1 1 0 1000. step param c list 0. 5 e-6 1 e-6 3 e-6. tran 7 e-6 7 e-3 0 7 e-6. probe. end c 1 = 3 e-6

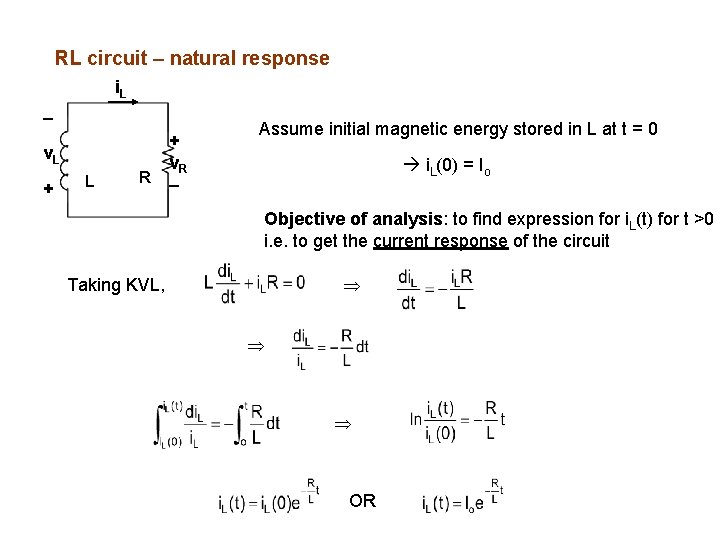
RL circuit – natural response i. L v. L + L R + v. R Assume initial magnetic energy stored in L at t = 0 i. L(0) = Io Objective of analysis: to find expression for i. L(t) for t >0 i. e. to get the current response of the circuit Taking KVL, OR

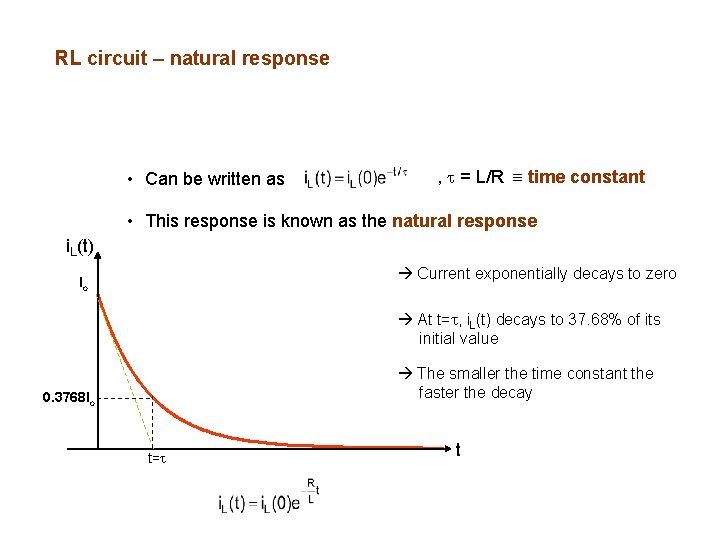
RL circuit – natural response • Can be written as , = L/R time constant • This response is known as the natural response i. L(t) Current exponentially decays to zero Io At t= , i. L(t) decays to 37. 68% of its initial value The smaller the time constant the faster the decay 0. 3768 Io t= t

RL circuit – natural response The inductor voltage is given by: And the voltage across the resistor is given by The power absorbed by the resistor can be calculated as: The energy loss (as heat) in the resistor from 0 to t:

RL circuit – natural response As t , ER As t , energy initially stored in inductor will be dissipated in the resistor in the form of heat

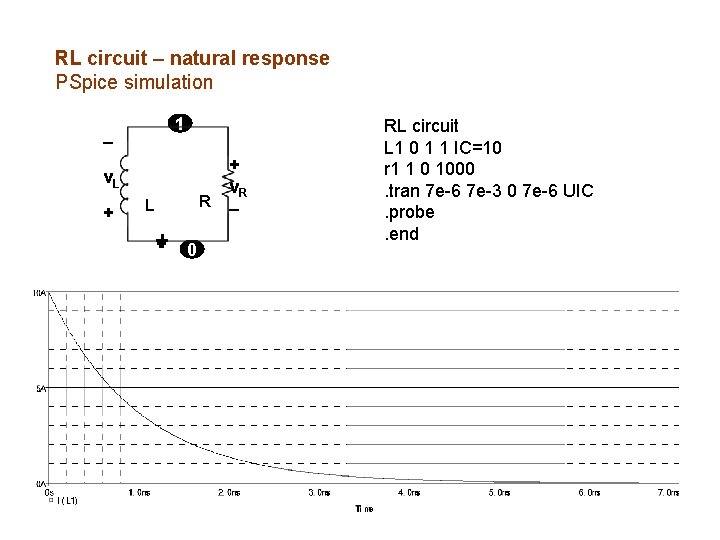
RL circuit – natural response PSpice simulation 1 v. L + R L 0 + v. R RL circuit L 1 0 1 1 IC=10 r 1 1 0 1000. tran 7 e-6 7 e-3 0 7 e-6 UIC. probe. end

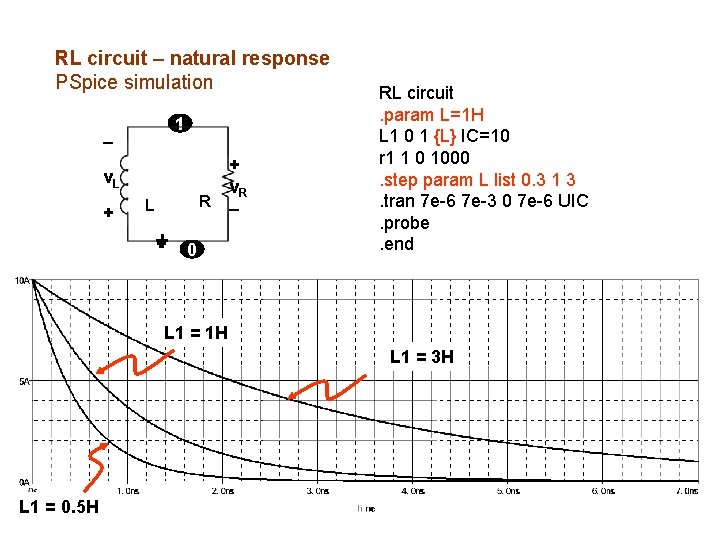
RL circuit – natural response PSpice simulation 1 v. L + R L 0 + v. R RL circuit. param L=1 H L 1 0 1 {L} IC=10 r 1 1 0 1000. step param L list 0. 3 1 3. tran 7 e-6 7 e-3 0 7 e-6 UIC. probe. end L 1 = 1 H L 1 = 3 H L 1 = 0. 5 H