First level analysis Model fitting at the within

First level analysis Model fitting at the within subject level methods for dummies 2009, Tessa Dekker

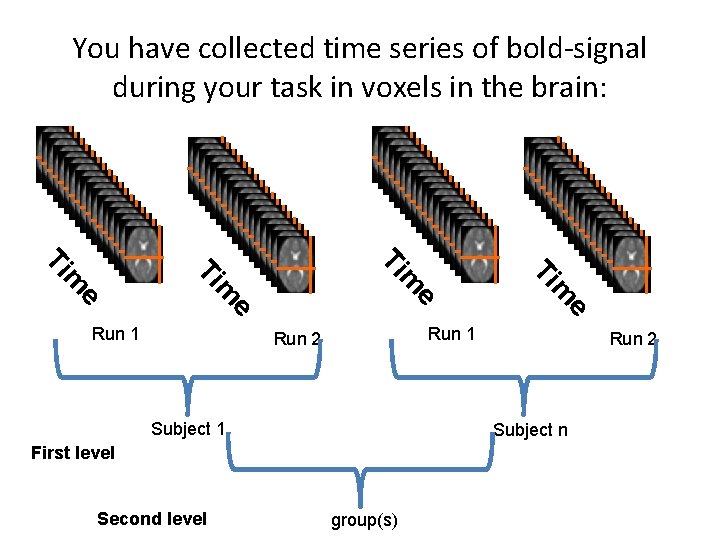
You have collected time series of bold-signal during your task in voxels in the brain: e e m m e Run 1 Run 2 Subject n First level Second level Ti Ti m e m Ti Ti Run 1 group(s)

You have preprocessed your data (realigning, filtering, spatial normalization etc. ) and are ready to go look for brain regions in which your experimental manipulation had an effect. Now what? First level analysis: Find out for each voxel in a subject to what extent it shows a response pattern you would expect based on your experimental manipulation or other things that you know may have impacted the signal.

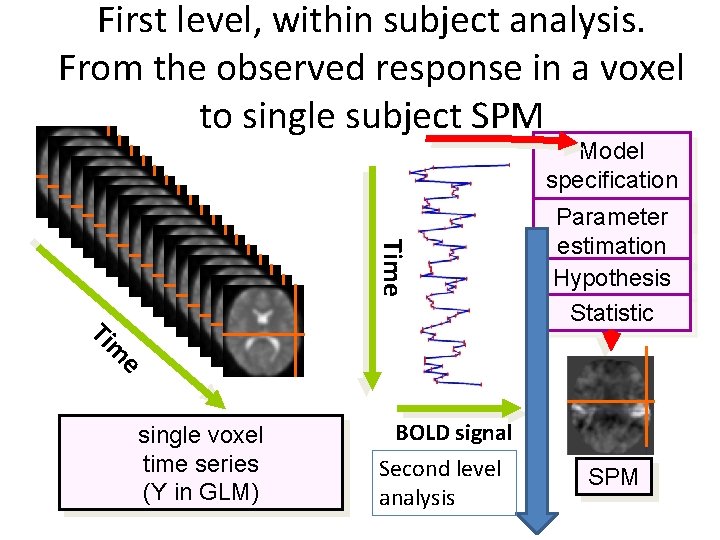
First level, within subject analysis. From the observed response in a voxel to single subject SPM Model specification nn Parameter Time estimation Hypothesis Statistic e m Ti single voxel time series (Y in GLM) BOLD signal Second level analysis SPM

Outline: • Modeling the BOLD-response; the design matrix • The GLM and parameter estimation • T and F contrasts and parametric designs • Statistical inference • An SPM example • Some remarks on orthogonal contrasts

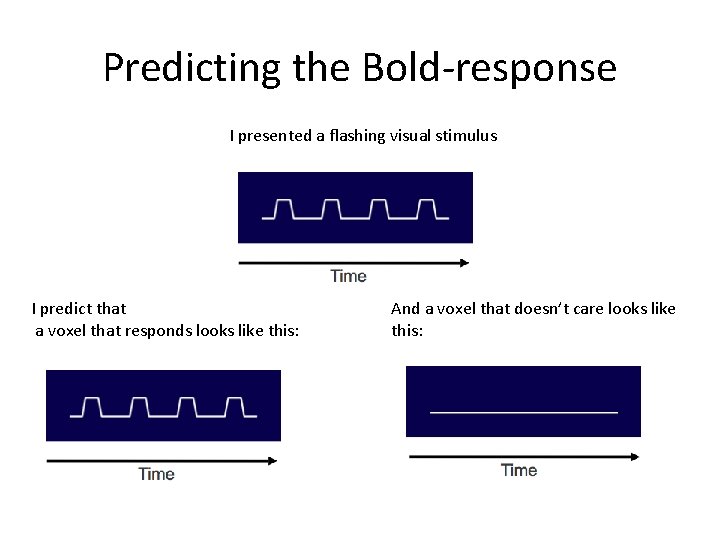
Predicting the Bold-response I presented a flashing visual stimulus I predict that a voxel that responds looks like this: And a voxel that doesn’t care looks like this:

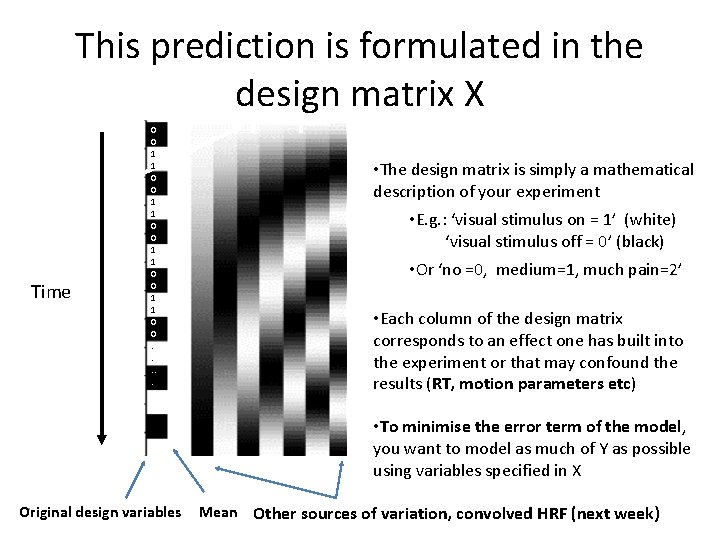
This prediction is formulated in the design matrix X Time 0 0 1 1 0 0. . . • The design matrix is simply a mathematical description of your experiment • E. g. : ‘visual stimulus on = 1’ (white) ‘visual stimulus off = 0’ (black) • Or ‘no =0, medium=1, much pain=2’ • Each column of the design matrix corresponds to an effect one has built into the experiment or that may confound the results (RT, motion parameters etc) • To minimise the error term of the model, you want to model as much of Y as possible using variables specified in X 7 Original design variables Mean Other sources of variation, convolved HRF (next week)

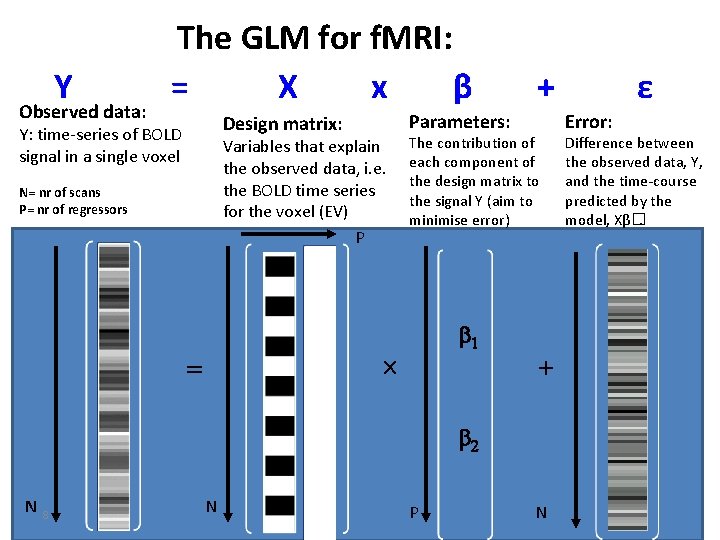
Y Observed data: The GLM for f. MRI: = X x β Parameters: Design matrix: Y: time-series of BOLD signal in a single voxel Variables that explain the observed data, i. e. the BOLD time series for the voxel (EV) P N= nr of scans P= nr of regressors The contribution of each component of the design matrix to the signal Y (aim to minimise error) b 1 ´ = + + b 2 N 8 N P N ε Error: Difference between the observed data, Y, and the time-course predicted by the model, Xβ�.

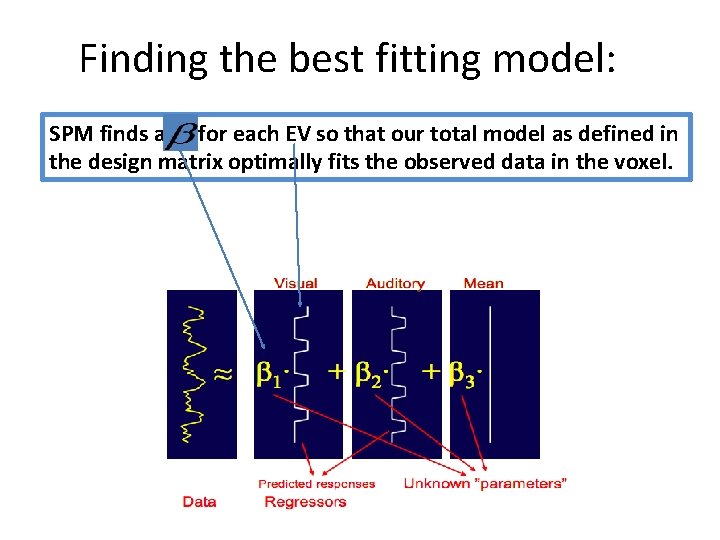
Finding the best fitting model: SPM finds a for each EV so that our total model as defined in the design matrix optimally fits the observed data in the voxel.

Finding the best fitting model: These optimal fitting values are saved in beta image files for each EV. The residual signal variance in the voxel, unexplained by the model (within subject error) is saved in MSres image files.

Methods: • Variational Bayes: allows for spatial priors for regression and regularized voxel-wise models for noise processing, see SPM manual or book • Least squares method (classic): finds which linear combination of X variables in design matrix results in minimal difference between observed data and predicted data by Minimizing: Gives:

Contrasts • But usually we are not interested in the whole model – What variation in the signal is the result of a visual stimulus and not of movement? • A contrast selects a specific effect of interest: – a contrast c is a vector of the length of the number of EVs in the design matrix. – c. Tβ is a linear combination of regression coefficients β. c. Tβ = 1 xb 1 + 0 xb 2 + 0 xb 3 + 0 xb 4 + 0 xb 5 +. . . c. T = [1 0 0 …] c. Tβ = 0 xb 1 + -1 xb 2 + 1 xb 3 + 0 xb 4 + 0 xb 5 +. . . c. T = [0 -1 1 0 0 …] • SPM saves these linear combinations of coefficients as contrast images and feeds them up to higher level analysis

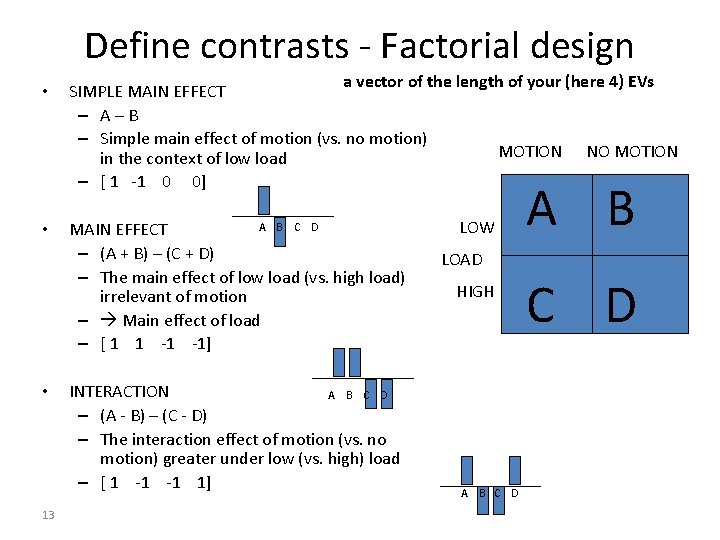
Define contrasts - Factorial design • • • 13 a vector of the length of your (here 4) EVs SIMPLE MAIN EFFECT – A–B – Simple main effect of motion (vs. no motion) MOTION NO MOTION in the context of low load – [ 1 -1 0 0] A B C D MAIN EFFECT – (A + B) – (C + D) – The main effect of low load (vs. high load) irrelevant of motion – Main effect of load – [ 1 1 -1 -1] INTERACTION A B C D – (A - B) – (C - D) – The interaction effect of motion (vs. no motion) greater under low (vs. high) load – [ 1 -1 -1 1] LOW A B LOAD HIGH A B C D

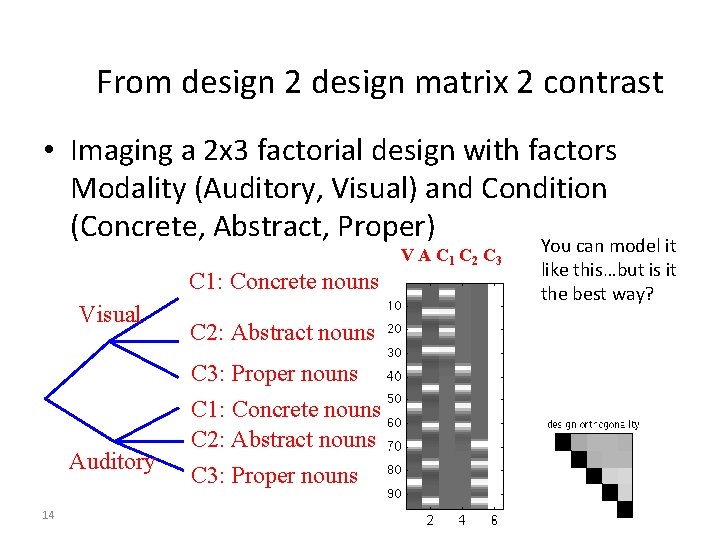
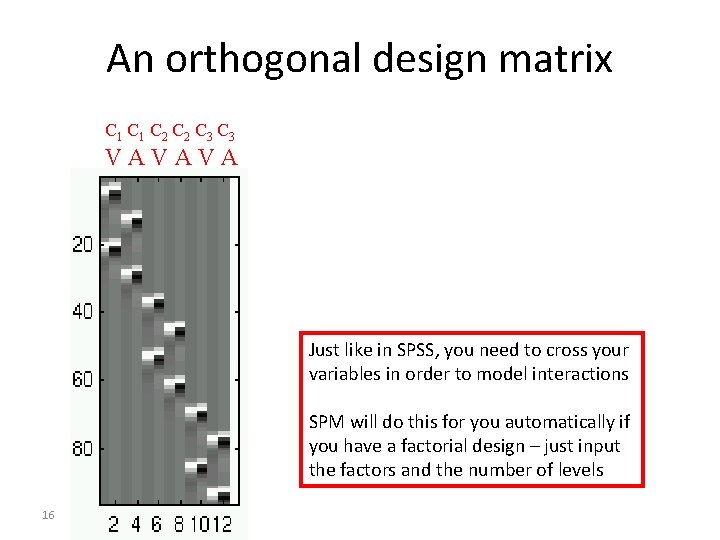
From design 2 design matrix 2 contrast • Imaging a 2 x 3 factorial design with factors Modality (Auditory, Visual) and Condition (Concrete, Abstract, Proper) You can model it C 1: Concrete nouns Visual Auditory 14 C 2: Abstract nouns C 3: Proper nouns C 1: Concrete nouns C 2: Abstract nouns C 3: Proper nouns V A C 1 C 2 C 3 like this…but is it the best way?

What can we test with this design matrix? V A C 1 C 2 C 3 We can test for main effects: - Visual > Auditory? C: [1 -1 0 0 0] - Concrete > Abstract? C: [0 0 1 -1 0] But we can’t test for interactions or simple main effects: Visual/concrete > Auditory/concrete? ? ? 15

An orthogonal design matrix C 2 C 1 C 2 C 3 VAVAVA C 3 V A Just like in SPSS, you need to cross your variables in order to model interactions SPM will do this for you automatically if you have a factorial design – just input the factors and the number of levels 16

Statistical inference • For each voxel, we estimated the value of the regression coefficient for each variable (column) in our model (design matrix) • We defined contrasts to pick out variables or combinations of variables of interest in our model • a large value of c. X reflects a large effect size (% signal change) of our contrast of interest • But data is noisy- so can we trust these effects are not due to chance? ? • To find this out SPM can calculate t and f-test statistical maps for each contrast using beta images, contrasts, residual variance maps and means.

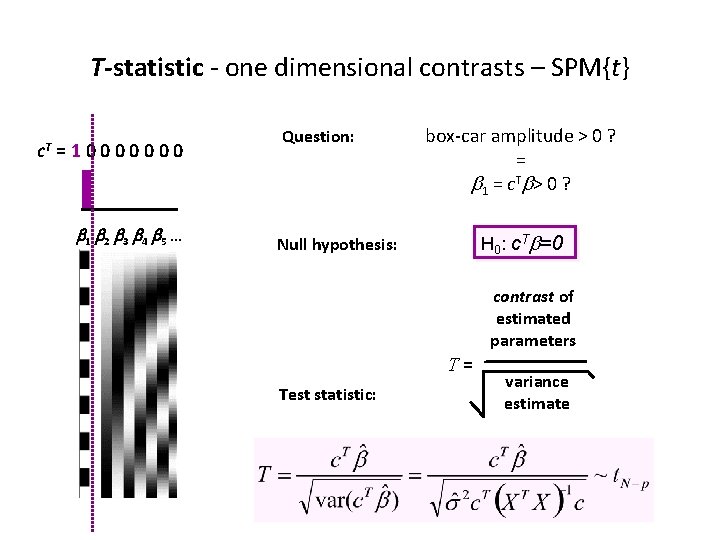
T-statistic - one dimensional contrasts – SPM{t} c. T =10000000 b 1 b 2 b 3 b 4 b 5. . . Question: box-car amplitude > 0 ? = b 1 = c. Tb> 0 ? H 0: c. Tb=0 Null hypothesis: contrast of estimated parameters T= Test statistic: variance estimate

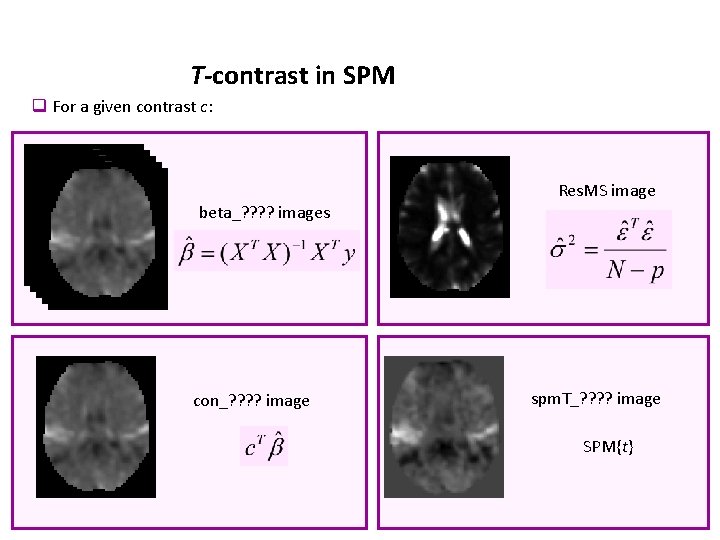
T-contrast in SPM q For a given contrast c: Res. MS image beta_? ? images con_? ? image spm. T_? ? image SPM{t}

F-statistic • F-tests can be viewed as testing for the additional variance explained by a larger model compared to a simpler model • Tests a weighted sum of squares of one or several linear combinations of the regression coefficients: is bidirectional (squared t -test) • Contrasts and hypotheses:

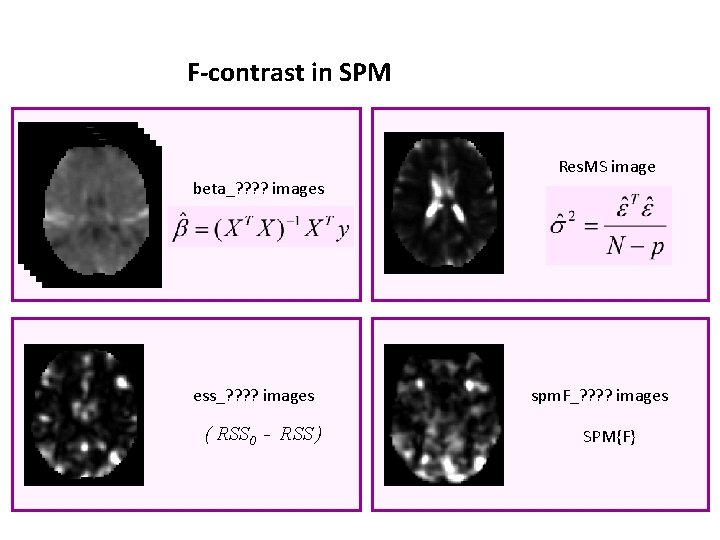
F-contrast in SPM Res. MS image beta_? ? images ess_? ? images ( RSS 0 - RSS ) spm. F_? ? images SPM{F}

Hypothesis Testing u q Type I Error α: Acceptable false positive rate α. Level threshold uα Threshold uα controls the false positive rate Observation of test statistic t, a realisation of T q P-value: A p-value summarises evidence against H 0. This is the change of observing value more extreme than t under the null hypothesis. q The conclusion about the hypothesis: We reject the null hypothesis in favour of the alternative hypothesis if t > uα Null Distribution of T t P-val Null Distribution of T

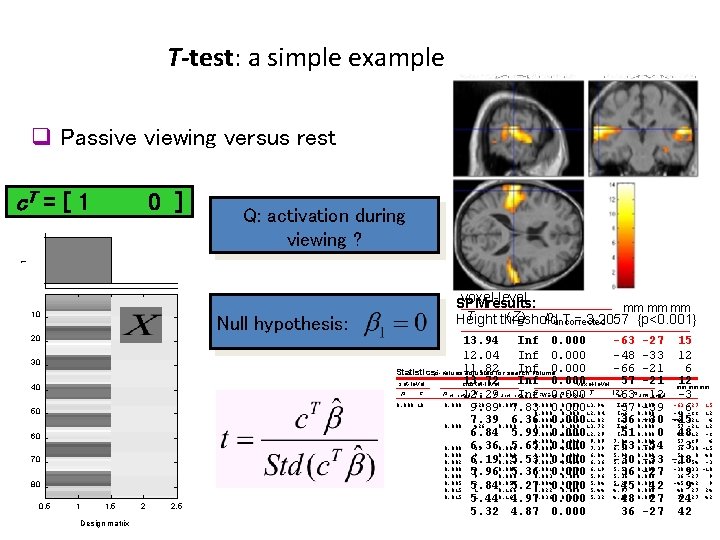
T-test: a simple example q Passive viewing versus rest c. T = [ 1 Q: activation during viewing ? 1 0 ] 10 Null hypothesis: 20 30 40 50 60 70 80 0. 5 1 1. 5 Design matrix 2 2. 5 voxel-level SPMresults: mm mm mm ( ) T Z p Height threshold T = 3. 2057 {p<0. 001} uncorrected º 13. 94 Inf 0. 000 -63 -27 15 12. 04 Inf 0. 000 -48 -33 12 11. 82 Inf 0. 000 -66 -21 6 Statistics: p-values adjusted for search volume 13. 72 Inf 0. 000 57 -21 mm 12 mm mm set-level cluster-level voxel-level (Z ) p corrected k E p FDR-corr T p º 63 uncorrected 12. 29 p uncorrected Infp FWE-corr 0. 000 -12 -3 0. 000 10 0. 000 520 0. 000 13. 94 Inf 9. 89 7. 830. 000 57 0. 000 -39 -63 6 -27 15 0. 000 12. 04 Inf 0. 000 -48 -33 12 0. 000 11. 82 Inf -66 -21 6 7. 39 6. 360. 000 36 0. 000 -30 -15 0. 000 426 0. 000 13. 72 Inf 0. 000 57 -21 12 0. 000 12. 29 Inf 6. 84 5. 990. 000 51 0. 000 0 6348 -12 -3 0. 000 9. 89 7. 83 0. 000 57 -39 6 5. 650. 000 -63 -54 36 -3 -30 -15 0. 000 6. 36 35 0. 000 7. 39 6. 36 0. 000 9 0. 000 6. 84 5. 99 0. 000 51 0 48 5. 530. 000 -33 -18 0. 002 6. 19 3 0. 024 0. 0010. 000 6. 36 5. 65 0. 000 -63 -54 -3 0. 000 8 0. 001 0. 000 6. 19 5. 53 0. 000 -33 -18 5. 360. 0030. 000 36 0. 000 -27 36 9 -27 9 0. 000 5. 96 5. 36 0. 005 2 0. 058 0. 004 0. 000 5. 84 5. 270. 0220. 000 -45 42 -45 942 9 0. 015 1 0. 166 0. 000 5. 44 4. 97 0. 000 48 27 24 0. 015 1 0. 166 0. 036 0. 000 5. 32 4. 87 0. 000 36 -27 42 5. 44 4. 97 0. 000 48 27 24 5. 32 4. 87 0. 000 36 -27 42

Final remarks: • Some designs are less efficient than others • If EVs are correlated it is hard to disentangle which one drives the effect in the voxel, resulting in less power to detect a unique effect of that EV (e. g. : button press and target detection) • SPM gives you an estimation of this problem in the orthogonality matrix – depicts the magnitude of the cosine of the angle between the EVs as indicator of correlation (Dark is close to 1, highly correlated. White means Evs are orthogonal or uncorrelated, good).

References • • • MFD slides 2007 Short SPM course slides (by Guillaume) FSL course slides SPM manual SPM book, chapter 1, 7 and 8