FIRST and FOLLOW Lecture 8 Mon Feb 9

FIRST and FOLLOW Lecture 8 Mon, Feb 9, 2004

Left Factoring l l l A minor problem occurs when two productions for the same nonterminal begin with the same token. We cannot decide which production to use. This is not necessarily a problem since we could process the part they have in common, then make a decision based on what follows.

Left Factoring l l l Consider the grammar A | . We use left factorization to transform it into the form A A' A' | . Now we can apply the productions immediately and unambiguously.

Example: Left Factoring l l In the earlier example, we had the productions C id == num | id != num | id < num To perform left factoring, introduce a nonterminal C': C id C' C' == num | != num | < num

Example: Left Factoring l l Consider the grammar of if statements. S if C then S else S | if C then S We rewrite it as S if C then S S' S' else S | .

LL Parsing Methods l LL parsing methods read the tokens from Left to right and parse them top-down according to a Leftmost derivation.

Table-Driven LL Parsing l To build the parsing table, we need the notion of nullability and two functions l l FIRST FOLLOW

Nullability l l l A nonterminal A is nullable if A * . Clearly, A is nullable if it has a production A . But A is also nullable if there are, for example, productions A BC. B A | a. C | . C a. B | Cb | .

Nullability l In other words, A is nullable if there is a production A , or there is a production A B 1 B 2…Bn, where B 1, B 2, . . . , Bn are nullable.

Nullability l l In the grammar E T E' E' + T E' | . T F T' T' * F T' | . F (E) | id | num E' and T' are nullable. E, T, and F are not nullable.

Summary Nonterminal E E' T T' F Nullable No Yes No

FIRST and FOLLOW l Given a grammar G, we may define the functions FIRST and FOLLOW on the strings of symbols of G. l l FIRST( ) is the set of all terminals that may appear as the first symbol in a replacement string of . FOLLOW( ) is the set of all terminals that may follow in a derivation.

FIRST l For a grammar symbol X, FIRST(X) is defined as follows. l l For every terminal X, FIRST(X) = {X}. For every nonterminal X, if X Y 1 Y 2…Yn is a production, then l l FIRST(Y 1) FIRST(X). Furthermore, if Y 1, Y 2, …, Yk are nullable, then FIRST(Yk + 1) FIRST(X).

FIRST l l l We are concerned about FIRST(X) only for the nonterminals of the grammar. FIRST(X) for terminals is trivial. According to the definition, to determine FIRST(A), we must inspect all productions that have A on the left.

Example: FIRST l Let the grammar be E T E' E' + T E' | . T F T' T' * F T' | . F (E) | id | num

Example: FIRST l Find FIRST(E). l l l E occurs on the left in only one production E T E'. Therefore, FIRST(T) FIRST(E). Furthermore, T is not nullable. Therefore, FIRST(E) = FIRST(T). We have yet to determine FIRST(T).

Example: FIRST l Find FIRST(T). l l l T occurs on the left in only one production T F T'. Therefore, FIRST(F) FIRST(T). Furthermore, F is not nullable. Therefore, FIRST(T) = FIRST(F). We have yet to determine FIRST(F).

Example: FIRST l Find FIRST(F). l l FIRST(F) = {(, id, num}. Therefore, l l FIRST(E) = {(, id, num}. FIRST(T) = {(, id, num}.

Example: FIRST l Find FIRST(E'). l l FIRST(E') = {+}. Find FIRST(T'). l FIRST(T') = {*}.

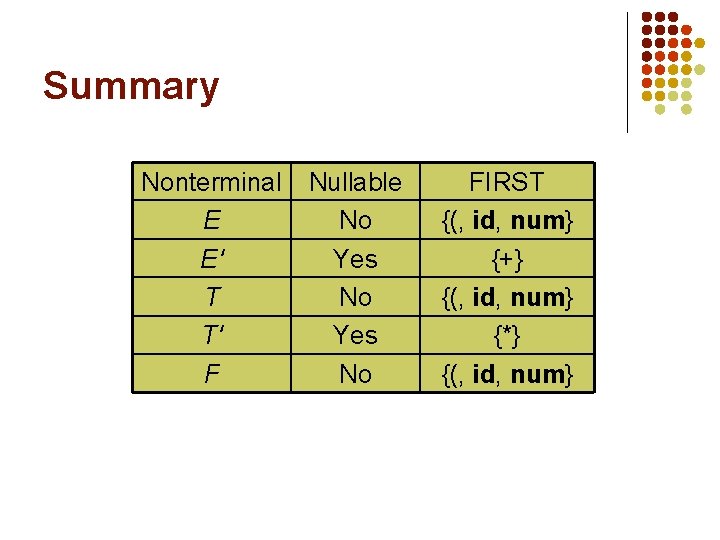
Summary Nonterminal E E' T T' F Nullable No Yes No FIRST {(, id, num} {+} {(, id, num} {*} {(, id, num}

FOLLOW l For a grammar symbol X, FOLLOW(X) is defined as follows. l l l If S is the start symbol, then $ FOLLOW(S). If A B is a production, then FIRST( ) FOLLOW(B). If A B is a production, or A B is a production and is nullable, then FOLLOW(A) FOLLOW(B).

FOLLOW l l We are concerned about FOLLOW(X) only for the nonterminals of the grammar. According to the definition, to determine FOLLOW(A), we must inspect all productions that have A on the right.

Example: FOLLOW l Let the grammar be E T E' E' + T E' | . T F T' T' * F T' | . F (E) | id | num

Example: FOLLOW l Find FOLLOW(E). l l l E is the start symbol, therefore $ FOLLOW(E). E occurs on the right in only one production. F (E). Therefore FOLLOW(E) = {$, )}.

Example: FOLLOW l Find FOLLOW(E'). l l E' occurs on the right in two productions. E T E' E' + T E'. Therefore, FOLLOW(E') = FOLLOW(E) = {$, )}.

Example: FOLLOW l Find FOLLOW(T). l l T occurs on the right in two productions. E T E' E' + T E'. Therefore, FOLLOW(T) contains FIRST(E') = {+}. However, E' is nullable, therefore it also contains FOLLOW(E) = {$, )} and FOLLOW(E') = {$, )}. Therefore, FOLLOW(T) = {+, $, )}.

Example: FOLLOW l Find FOLLOW(T'). l l T' occurs on the right in two productions. T F T' T' * F T'. Therefore, FOLLOW(T') = FOLLOW(T) = {$, ), +}.

Example: FOLLOW l Find FOLLOW(F). l l F occurs on the right in two productions. T F T' T' * F T'. Therefore, FOLLOW(F) contains FIRST(T') = {*}. However, T' is nullable, therefore it also contains FOLLOW(T) = {+, $, )} and FOLLOW(T') = {$, ), +}. Therefore, FOLLOW(F) = {*, $, ), +}.

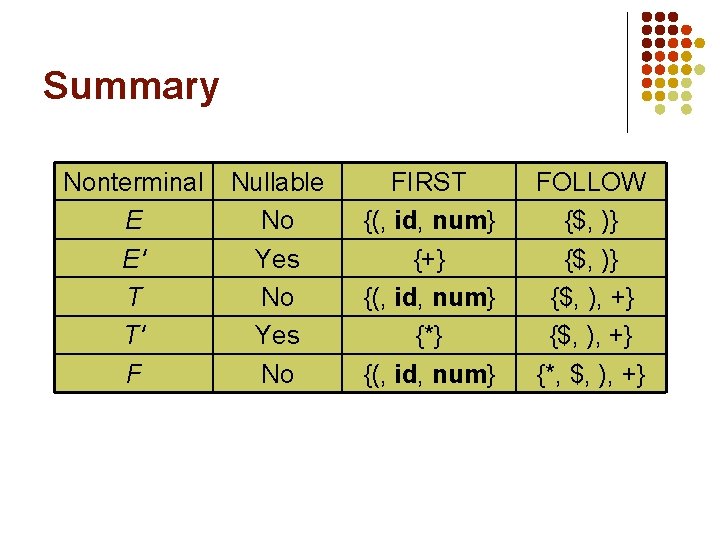
Summary Nonterminal E E' T T' F Nullable No Yes No FIRST {(, id, num} {+} {(, id, num} {*} {(, id, num} FOLLOW {$, )} {$, ), +} {*, $, ), +}

Exercise l l The grammar R R R | R* | (R) | a | b generates all regular expressions on the alphabet {a, b}. Using the result of the exercise from the previous Lecture, find FIRST(X) and FOLLOW(X) for each nonterminal X in the grammar.