FIR and IIR Filter Design Techniques FIR IIR

FIR and IIR Filter Design Techniques FIR 與 IIR 濾波器設計技巧 o o o Speaker: Wen-Fu Wang 王文阜 Advisor: Jian-Jiun Ding 丁建均 教授 E-mail: r 96942061@ntu. edu. tw Graduate Institute of Communication Engineering National Taiwan University, Taipei, Taiwan, ROC Feb. 2008 DISP Lab 1

Outline o Introduction o IIR Filter Design by Impulse invariance method o IIR Filter Design by Bilinear transformation method o FIR Filter Design by Window function technique Feb. 2008 DISP Lab 2

Outline o FIR Filter Design by Frequency sampling technique o FIR Filter Design by MSE o Conclusions o References Feb. 2008 DISP Lab 3

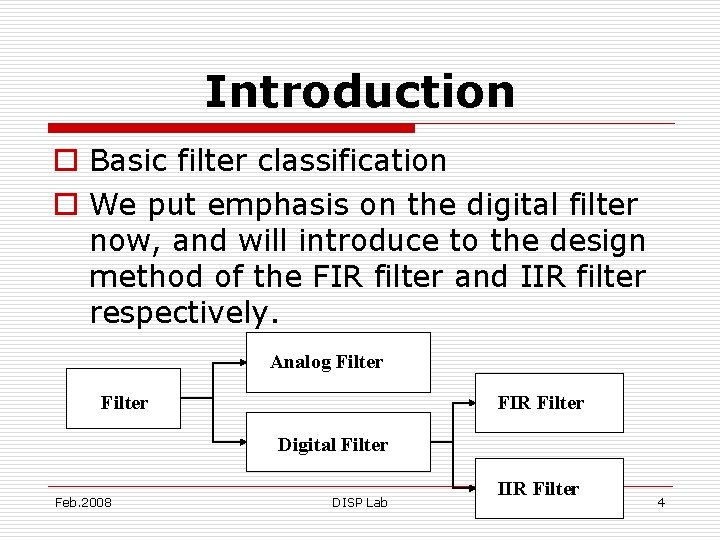
Introduction o Basic filter classification o We put emphasis on the digital filter now, and will introduce to the design method of the FIR filter and IIR filter respectively. Analog Filter FIR Filter Digital Filter Feb. 2008 DISP Lab IIR Filter 4

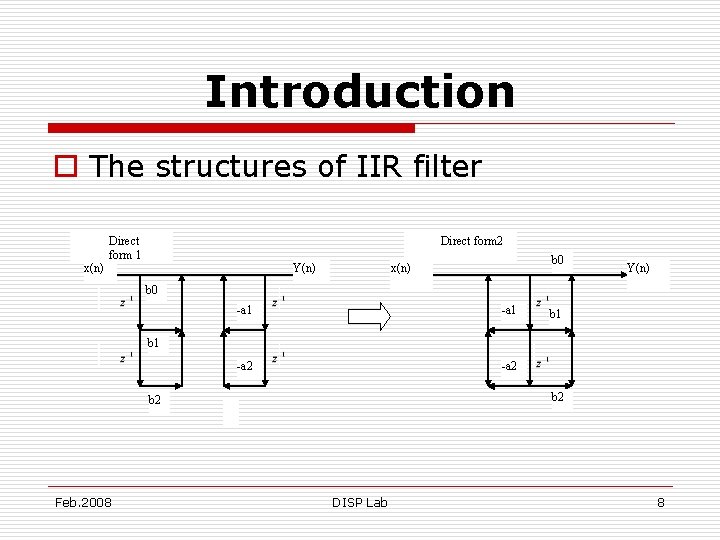
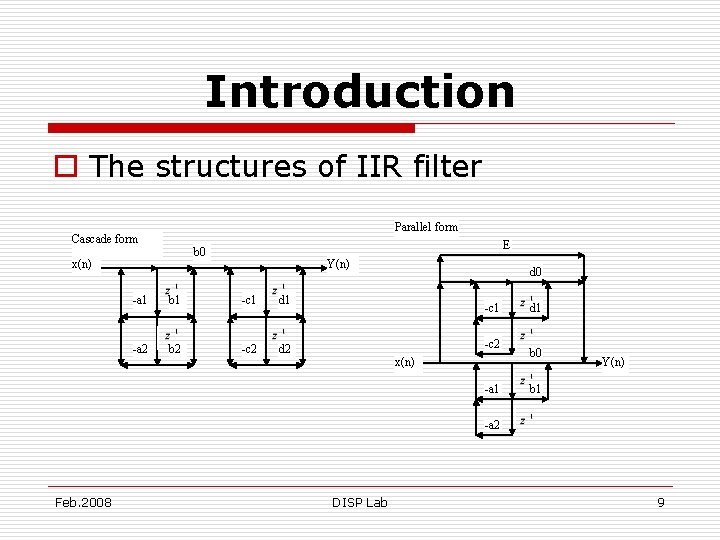
Introduction o IIR is the infinite impulse response abbreviation. o Digital filters by the accumulator, the multiplier, and it constitutes IIR filter the way, generally may divide into three kinds, respectively is Direct form, Cascade form, and Parallel form. Feb. 2008 DISP Lab 5

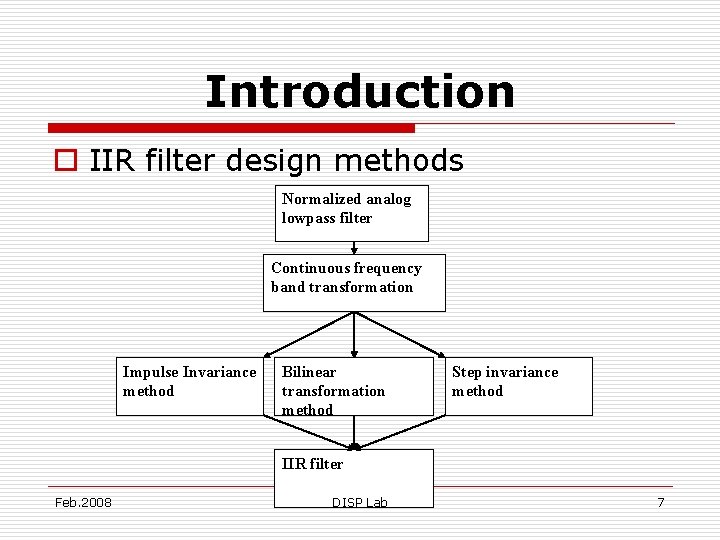
Introduction o IIR filter design methods include the impulse invariance, bilinear transformation, and step invariance. o We must emphasize at impulse invariance and bilinear transformation. Feb. 2008 DISP Lab 6

Introduction o IIR filter design methods Normalized analog lowpass filter Continuous frequency band transformation Impulse Invariance method Bilinear transformation method Step invariance method IIR filter Feb. 2008 DISP Lab 7

Introduction o The structures of IIR filter Direct form 1 Direct form 2 x(n) Y(n) b 0 -a 1 -a 2 b 1 b 2 Feb. 2008 DISP Lab 8

Introduction o The structures of IIR filter Parallel form Cascade form E b 0 x(n) Y(n) -a 1 b 1 -c 1 d 1 -a 2 b 2 -c 2 d 0 -c 1 -c 2 x(n) -a 1 d 1 b 0 Y(n) b 1 -a 2 Feb. 2008 DISP Lab 9

Introduction o FIR is the finite impulse response abbreviation, because its design construction has not returned to the part which gives. o Its construction generally uses Direct form and Cascade form. Feb. 2008 DISP Lab 10

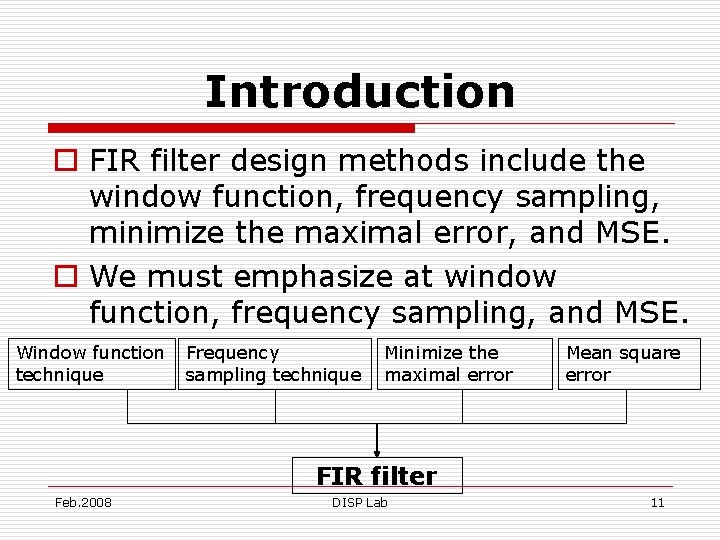
Introduction o FIR filter design methods include the window function, frequency sampling, minimize the maximal error, and MSE. o We must emphasize at window function, frequency sampling, and MSE. Window function technique Frequency sampling technique Minimize the maximal error Mean square error FIR filter Feb. 2008 DISP Lab 11

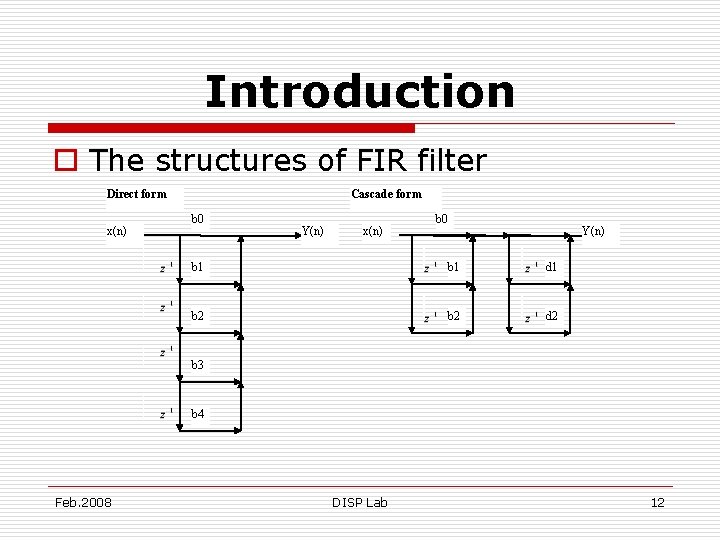
Introduction o The structures of FIR filter Direct form x(n) Cascade form b 0 Y(n) x(n) b 0 Y(n) b 1 d 1 b 2 d 2 b 3 b 4 Feb. 2008 DISP Lab 12

IIR Filter Design by Impulse invariance method o The most straightforward of these is the impulse invariance transformation o Let be the impulse response corresponding to , and define the continuous to discrete time transformation by setting o We sample the continuous time impulse response to produce the discrete time filter Feb. 2008 DISP Lab 13

IIR Filter Design by Impulse invariance method o The frequency response is the Fourier transform of the continuous time function and hence Feb. 2008 DISP Lab 14

IIR Filter Design by Impulse invariance method o The system function is o It is the many-to-one transformation from the s plane to the z plane. Feb. 2008 DISP Lab 15

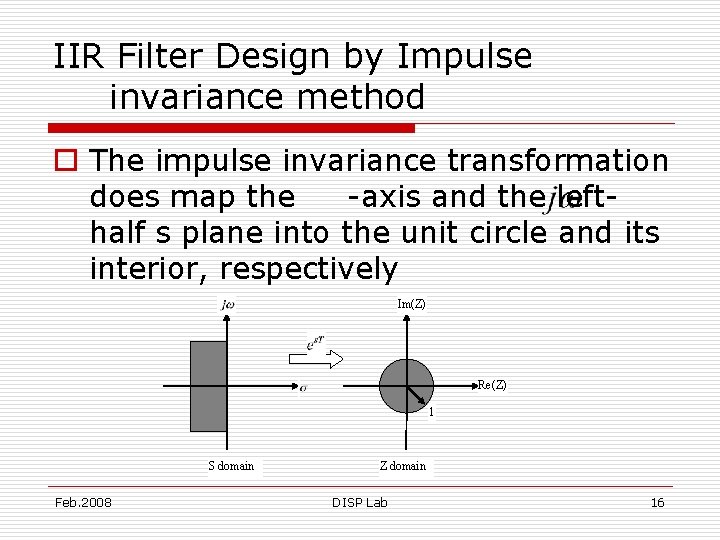
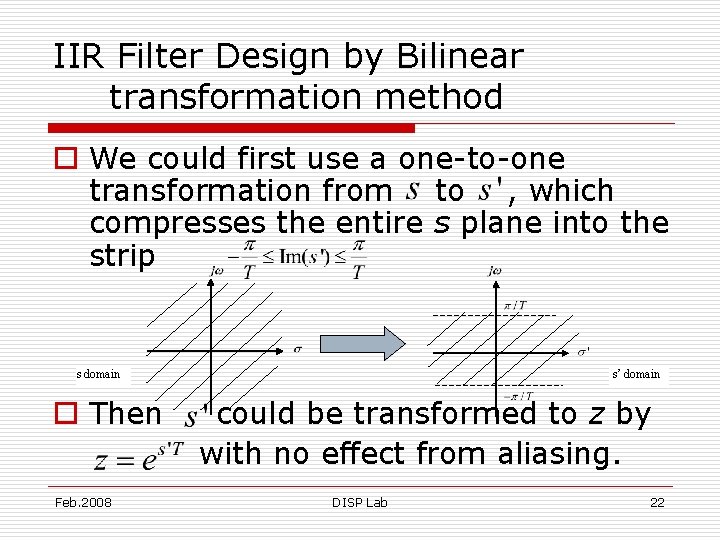
IIR Filter Design by Impulse invariance method o The impulse invariance transformation does map the -axis and the lefthalf s plane into the unit circle and its interior, respectively Im(Z) Re(Z) 1 S domain Feb. 2008 Z domain DISP Lab 16

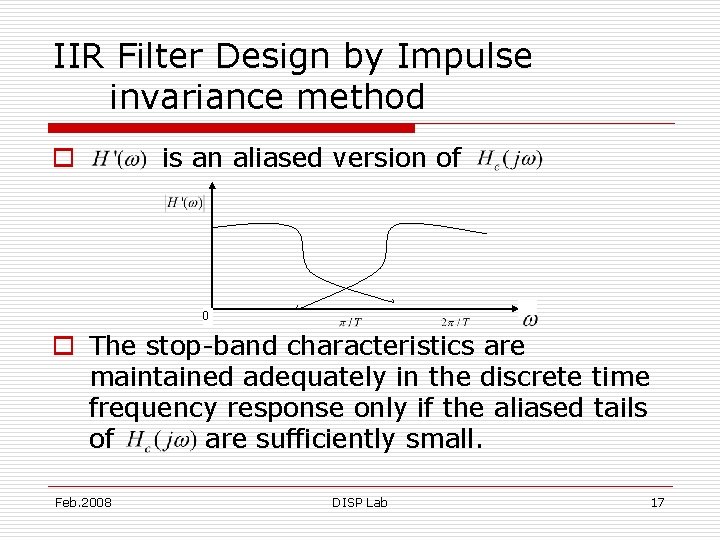
IIR Filter Design by Impulse invariance method o is an aliased version of 0 o The stop-band characteristics are maintained adequately in the discrete time frequency response only if the aliased tails of are sufficiently small. Feb. 2008 DISP Lab 17

IIR Filter Design by Impulse invariance method o The Butterworth and Chebyshev-I lowpass designs are more appropriate for impulse invariant transformation than are the Chebyshev-II and elliptic designs. o This transformation cannot be applied directly to highpass and bandstop designs. Feb. 2008 DISP Lab 18

IIR Filter Design by Impulse invariance method o is expanded a partial fraction expansion to produce o We have assumed that there are no multiple poles o And thus Feb. 2008 DISP Lab 19

IIR Filter Design by Impulse invariance method o Example: Expanding in a partial fraction expansion, it produce The impulse invariant transformation yields a discrete time design with the system function Feb. 2008 DISP Lab 20

IIR Filter Design by Bilinear transformation method o The most generally useful is the bilinear transformation. o To avoid aliasing of the frequency response as encountered with the impulse invariance transformation. o We need a one-to-one mapping from the s plane to the z plane. o The problem with the transformation is many-to-one. Feb. 2008 DISP Lab 21

IIR Filter Design by Bilinear transformation method o We could first use a one-to-one transformation from to , which compresses the entire s plane into the strip s domain o Then Feb. 2008 s’ domain could be transformed to z by with no effect from aliasing. DISP Lab 22

IIR Filter Design by Bilinear transformation method o The transformation from given by to is o The characteristic of this transformation is seen most readily from its effect on the axis. o Substituting and , we obtain Feb. 2008 DISP Lab 23

IIR Filter Design by Bilinear transformation method o The axis is compressed into the interval for in a one-toone method o The relationship between and is nonlinear, but it is approximately linear at small. Feb. 2008 DISP Lab 24

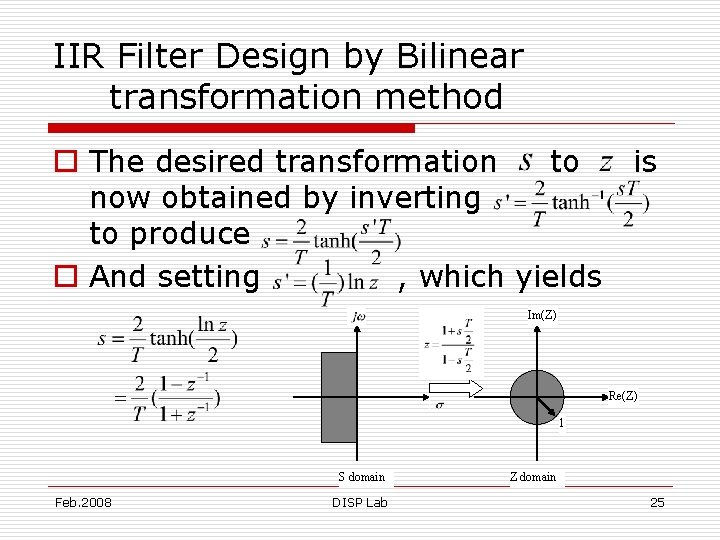
IIR Filter Design by Bilinear transformation method o The desired transformation to now obtained by inverting to produce o And setting , which yields is Im(Z) Re(Z) 1 S domain Feb. 2008 DISP Lab Z domain 25

IIR Filter Design by Bilinear transformation method o The discrete-time filter design is obtained from the continuous-time design by means of the bilinear transformation o Unlike the impulse invariant transformation, the bilinear transformation is one-to-one, and invertible. Feb. 2008 DISP Lab 26

FIR Filter Design by Window function technique o Simplest FIR the filter design is window function technique o A supposition ideal frequency response may express where Feb. 2008 DISP Lab 27

FIR Filter Design by Window function technique o To get this kind of systematic causal FIR to be approximate, the most direct method intercepts ideal impulse response! Feb. 2008 DISP Lab 28

FIR Filter Design by Window function technique o Truncation of the Fourier series produces the familiar Gibbs phenomenon o It will be manifested in , especially if is discontinuous. Feb. 2008 DISP Lab 29

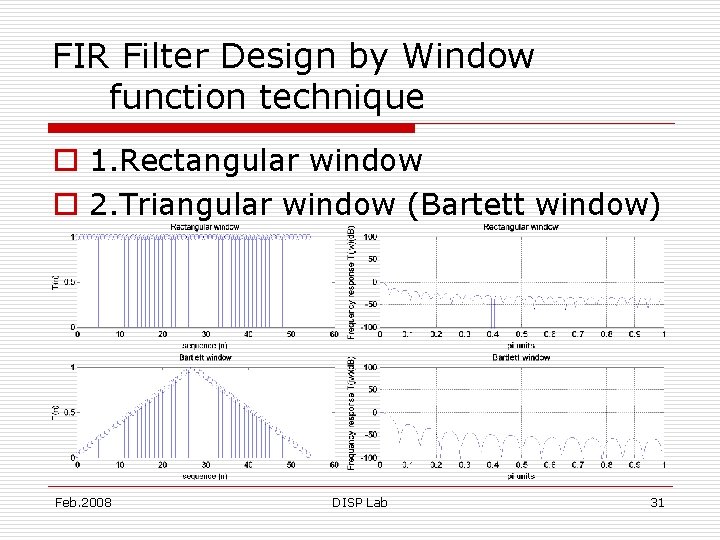
FIR Filter Design by Window function technique o 1. Rectangular window o 2. Triangular window (Bartett window) Feb. 2008 DISP Lab 30

FIR Filter Design by Window function technique o 1. Rectangular window o 2. Triangular window (Bartett window) Feb. 2008 DISP Lab 31

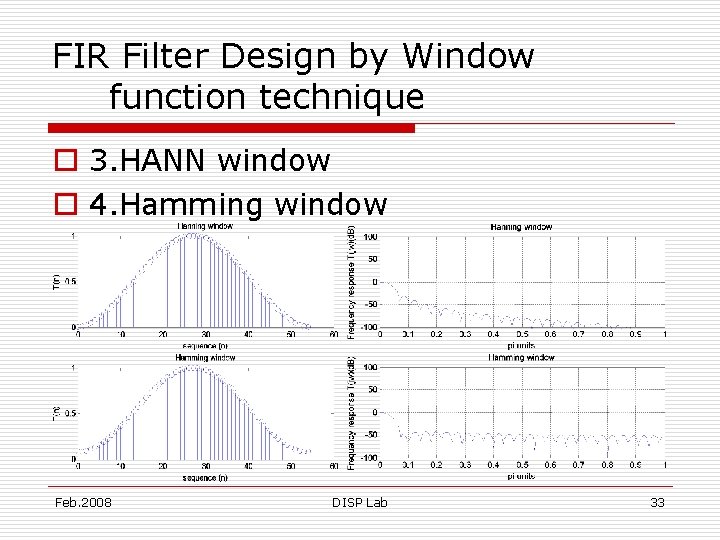
FIR Filter Design by Window function technique o 3. HANN window o 4. Hamming window Feb. 2008 DISP Lab 32

FIR Filter Design by Window function technique o 3. HANN window o 4. Hamming window Feb. 2008 DISP Lab 33

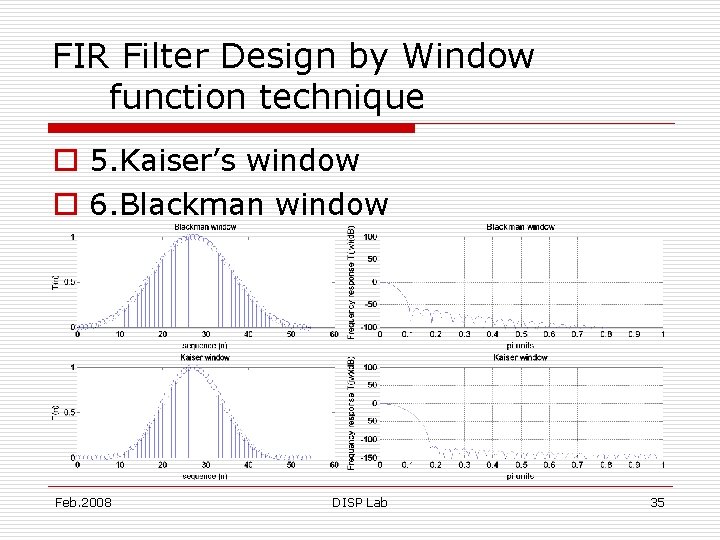
FIR Filter Design by Window function technique o 5. Kaiser’s window o 6. Blackman window Feb. 2008 DISP Lab 34

FIR Filter Design by Window function technique o 5. Kaiser’s window o 6. Blackman window Feb. 2008 DISP Lab 35

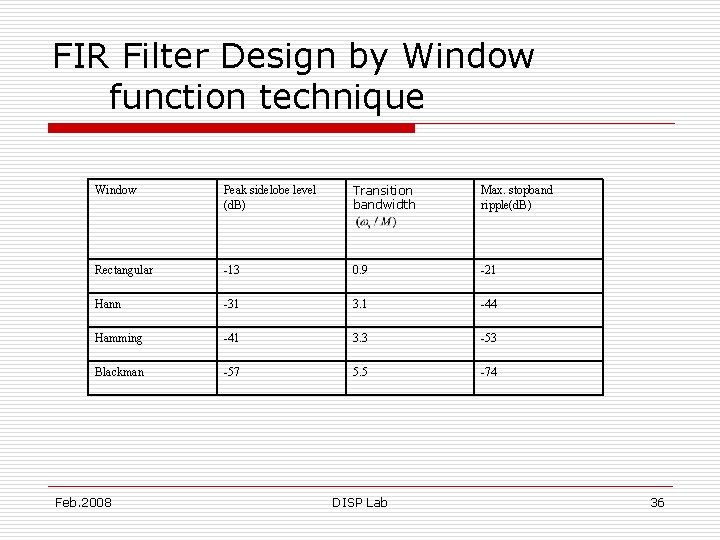
FIR Filter Design by Window function technique Window Peak sidelobe level (d. B) Transition bandwidth Max. stopband ripple(d. B) Rectangular -13 0. 9 -21 Hann -31 3. 1 -44 Hamming -41 3. 3 -53 Blackman -57 5. 5 -74 Feb. 2008 DISP Lab 36

FIR Filter Design by Frequency sampling technique o For arbitrary, non-classical specifications of , the calculation of , n=0, 1, …, M, via an appropriate approximation can be a substantial computation task. o It may be preferable to employ a design technique that utilizes specified values of directly, without the necessity of determining Feb. 2008 DISP Lab 37

FIR Filter Design by Frequency sampling technique o We wish to derive a linear phase IIR filter with real nonzero. The impulse response must be symmetric where are real and the integer part Feb. 2008 DISP Lab denotes 38

FIR Filter Design by Frequency sampling technique o It can be rewritten as where and o Therefore, it may write where Feb. 2008 DISP Lab 39

FIR Filter Design by Frequency sampling technique o with corresponding transform where o Hence which has a linear phase Feb. 2008 DISP Lab 40

FIR Filter Design by Frequency sampling technique o The magnitude response which has a maximum value at where Feb. 2008 DISP Lab 41

FIR Filter Design by Frequency sampling technique o The only nonzero contribution to at is from , and hence that o Therefore, by specifying the DFT samples of the desired magnitude response at the frequencies , and setting Feb. 2008 DISP Lab 42

FIR Filter Design by Frequency sampling technique o We produce a filter design from equation (5. 1) for which o The desired and actual magnitude responses are equal at the N frequencies Feb. 2008 DISP Lab 43

FIR Filter Design by Frequency sampling technique o In between these frequencies, is interpolated as the sum of the responses , and its magnitude does not, equal that of Feb. 2008 DISP Lab 44

FIR Filter Design by Frequency sampling technique o Example: For an ideal lowpass filter from choose , we would o The frequency samples indeed equal to the desired Feb. 2008 DISP Lab are 45

FIR Filter Design by Frequency sampling technique o The response is very similar to the result form using the rectangular window, and the stopband is similarly disappointing. o We can try to search for the optimum value of the transition sample would quickly lead us to a value of approximately , Feb. 2008 DISP Lab 46

FIR Filter Design by MSE : The spectrum of the filter we obtain o : The spectrum of the desired filter o o MSE= Feb. 2008 DISP Lab 47

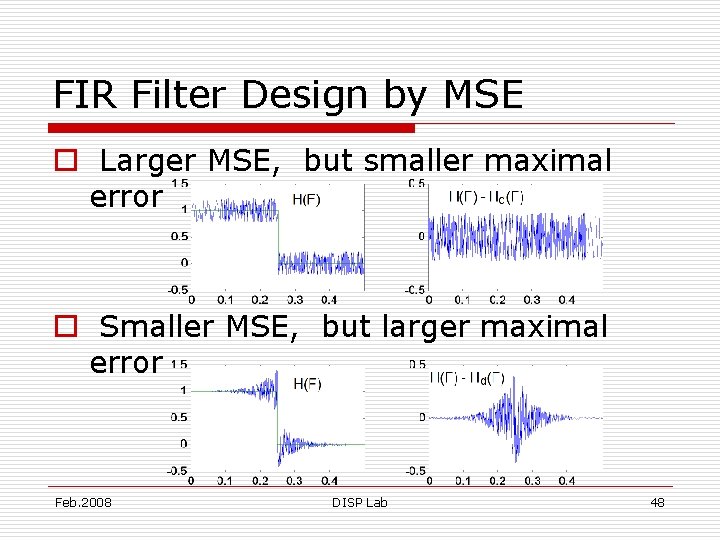
FIR Filter Design by MSE o Larger MSE, but smaller maximal error o Smaller MSE, but larger maximal error Feb. 2008 DISP Lab 48

FIR Filter Design by MSE o 1. Feb. 2008 DISP Lab 49

FIR Filter Design by MSE o 2. when n , when n = , n 0, when n = , n = 0, o 3. The formula can be repressed as: Feb. 2008 DISP Lab 50

FIR Filter Design by MSE o 4. Doing the partial differentiation: o 5. Minimize MSE: Feb. 2008 DISP Lab for all n’s 51

Conclusions o 1. 2. 3. 4. o 1. FIR advantage: Finite impulse response It is easy to optimalize Linear phase Stable FIR disadvantage: It is hard to implementation than IIR Feb. 2008 DISP Lab 52

Conclusions o 1. 2. 3. IIR advantage: It is easy to design It is easy to implementation IIR disadvantage: Infinite impulse response It is hard to optimalize than FIR Non-stable Feb. 2008 DISP Lab 53

References o [1]B. Jackson, Digital Filters and Signal Processing, Kluwer Academic Publishers 1986 o [2]Dr. De. Piero, Filter Design by Frequency Sampling, Cal. Poly State University o [3]W. James Mac. Lean, FIR Filter Design Using Frequency Sampling o [4]蒙以正, 數位信號處理, 旗標 2005 o [5]Maurice G. Bellanger, Adaptive Digital Filters second edition, Marcel dekker 2001 Feb. 2008 DISP Lab 54

References o [6] Lawrence R. Rabiner, Linear Program Design of Finite Impulse Response Digital Filters, IEEE 1972 o [7] Terrence J mc Creary, On Frequency Sampling Digital Filters, IEEE 1972 Feb. 2008 DISP Lab 55