Finite State Machines Presented by Hussein Bin Sama

Finite State Machines Presented by: Hussein Bin Sama && Tareq Alawneh Supervisor: Dr. Lo`ai Tawalbeh Real Time Embedded Systems

Outlines n FSM Introduction. n FSM Design. n VHDL Design of FSM. n FSM minimization. n Case Study. Real Time Embedded Systems

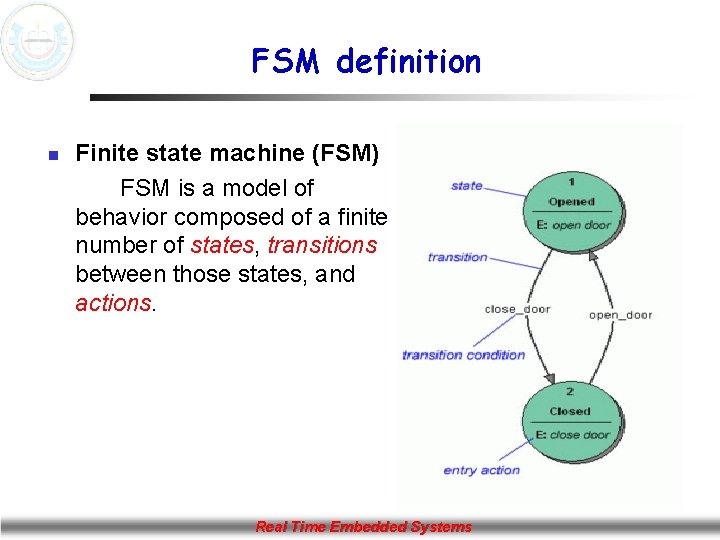
FSM definition n Finite state machine (FSM) FSM is a model of behavior composed of a finite number of states, transitions between those states, and actions. Real Time Embedded Systems

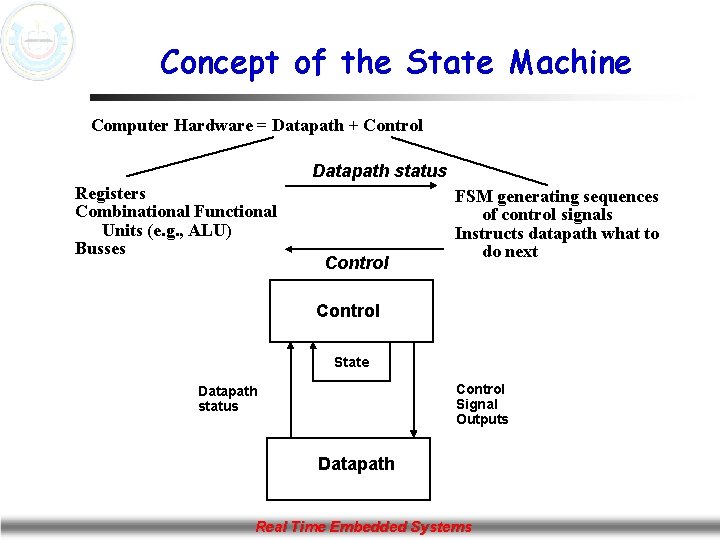
Concept of the State Machine Computer Hardware = Datapath + Control Datapath status Registers Combinational Functional Units (e. g. , ALU) Busses Control FSM generating sequences of control signals Instructs datapath what to do next Control State Control Signal Outputs Datapath status Datapath Real Time Embedded Systems

Mealy vs. Moore State Machines n n Finite State Machines (FSM) are of two types: Moore Machines n n n Next State = Function(Input, Present State) Output = Function(Present State) Mealy Machines n n Next State = Function(Input, Present State) Output = Function(Input, Present State) Real Time Embedded Systems

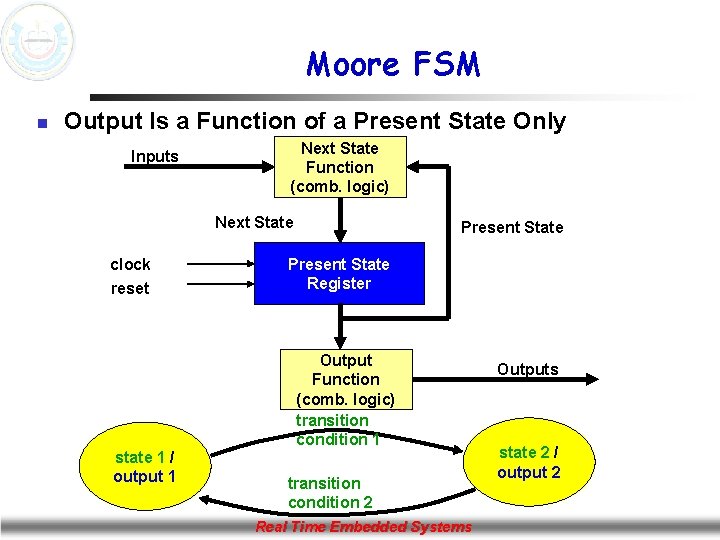
Moore FSM n Output Is a Function of a Present State Only Inputs Next State Function (comb. logic) Next State clock reset state 1 / output 1 Present State Register Output Function (comb. logic) transition condition 1 transition condition 2 Real Time Embedded Systems Outputs state 2 / output 2

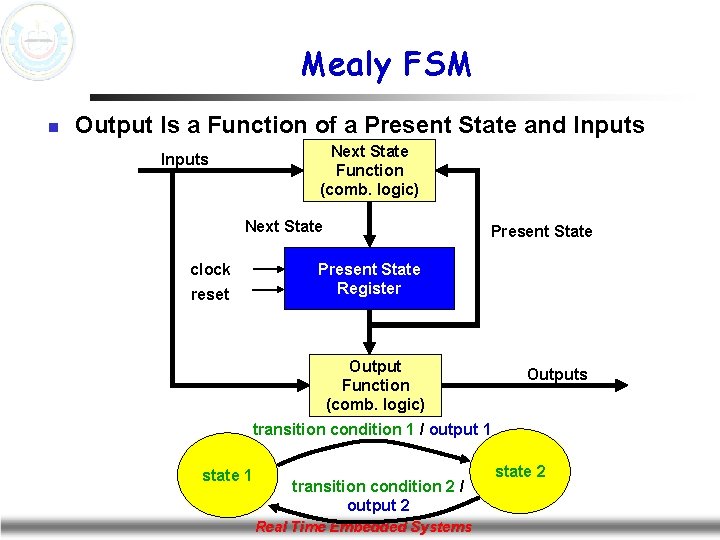
Mealy FSM n Output Is a Function of a Present State and Inputs Next State Function (comb. logic) Inputs Next State Present State Register clock reset Output Function (comb. logic) Outputs transition condition 1 / output 1 state 1 transition condition 2 / output 2 Real Time Embedded Systems state 2

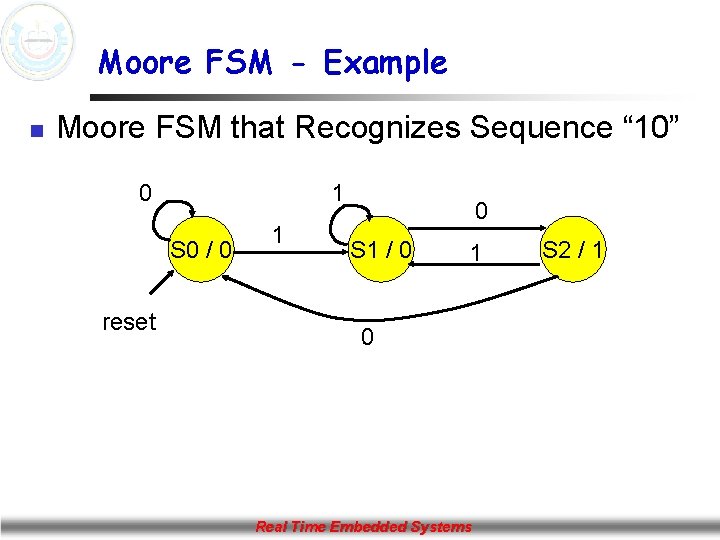
Moore FSM - Example n Moore FSM that Recognizes Sequence “ 10” 0 1 S 0 / 0 reset 1 0 S 1 / 0 1 0 Real Time Embedded Systems S 2 / 1

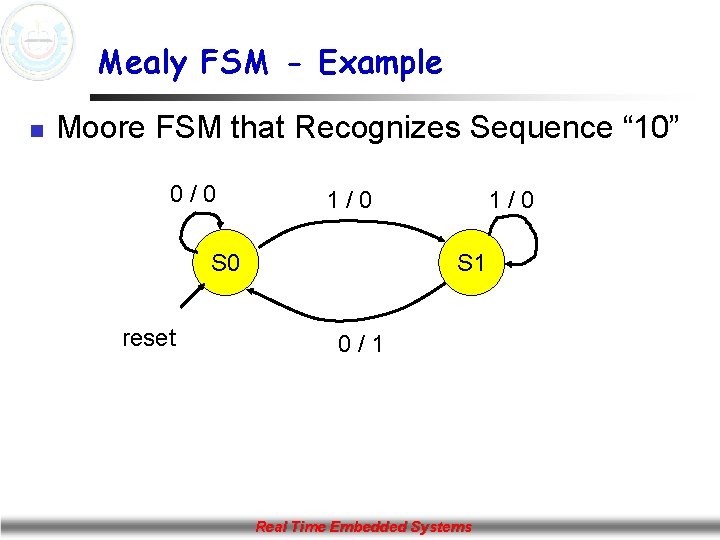
Mealy FSM - Example n Moore FSM that Recognizes Sequence “ 10” 0/0 1/0 S 0 reset 1/0 S 1 0/1 Real Time Embedded Systems

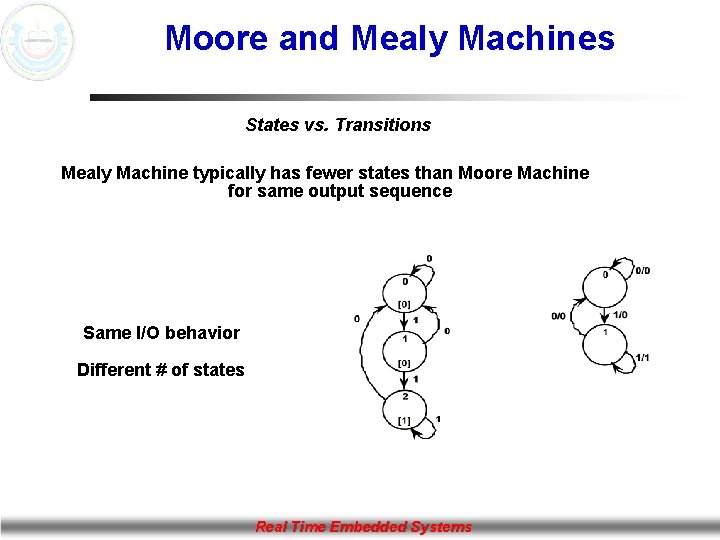
Moore and Mealy Machines States vs. Transitions Mealy Machine typically has fewer states than Moore Machine for same output sequence Same I/O behavior Different # of states Real Time Embedded Systems

Finite State Machine Word Problems Finite String Pattern Recognizer n A finite string recognizer has one input (X) and one output (Z ). The output is asserted whenever the input sequence … 010…has been observed, as long as the sequence 100 has never been seen. Real Time Embedded Systems

Finite State Machine Word Problems n Step 1. Understanding the problem statement Sample input/output behavior: X: 00101010010 Z: 00010101000 X: 11011010010 Z: 00000001000 Real Time Embedded Systems

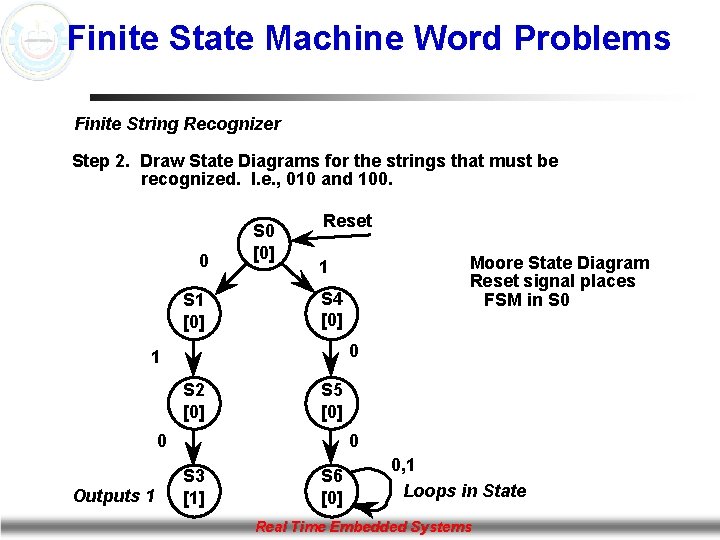
Finite State Machine Word Problems Finite String Recognizer Step 2. Draw State Diagrams for the strings that must be recognized. I. e. , 010 and 100. 0 S 1 [0] S 0 [0] Reset S 4 [0] 0 1 S 2 [0] S 5 [0] 0 Outputs 1 Moore State Diagram Reset signal places FSM in S 0 1 0 S 3 [1] S 6 [0] 0, 1 Loops in State Real Time Embedded Systems

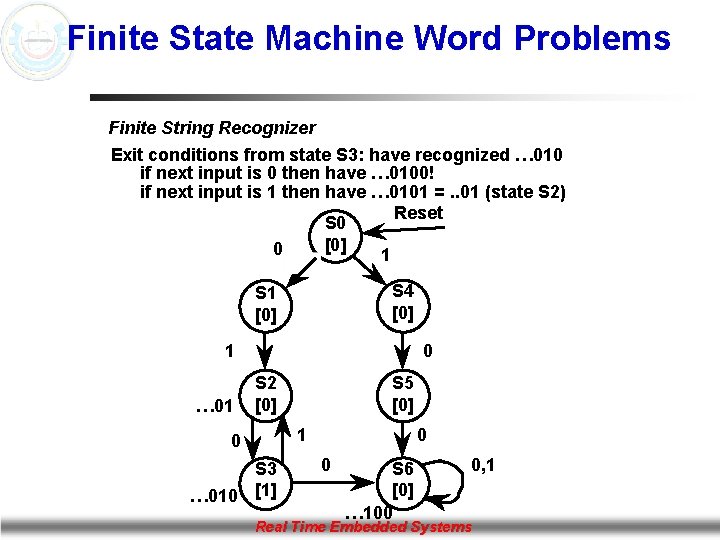
Finite State Machine Word Problems Finite String Recognizer Exit conditions from state S 3: have recognized … 010 if next input is 0 then have … 0100! if next input is 1 then have … 0101 =. . 01 (state S 2) Reset S 0 [0] 0 1 S 4 [0] S 1 [0] 1 … 01 0 S 2 [0] S 5 [0] 1 0 S 3 … 010 [1] 0 0 S 6 [0] … 100 0, 1 Real Time Embedded Systems

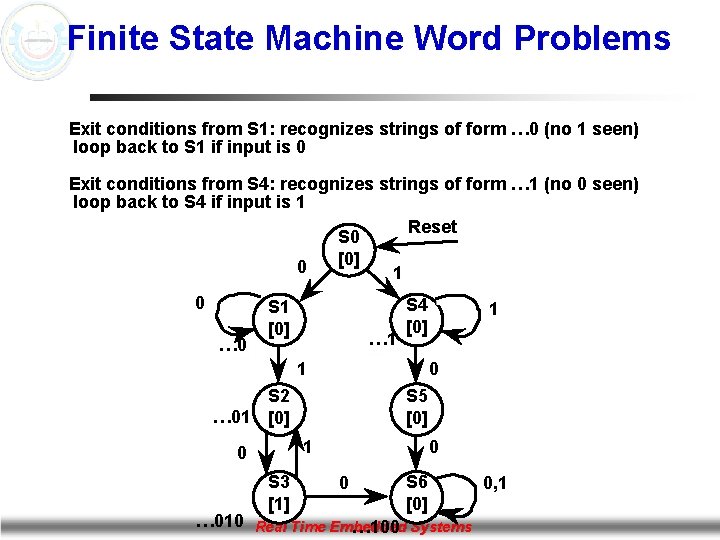
Finite State Machine Word Problems Exit conditions from S 1: recognizes strings of form … 0 (no 1 seen) loop back to S 1 if input is 0 Exit conditions from S 4: recognizes strings of form … 1 (no 0 seen) loop back to S 4 if input is 1 Reset S 0 [0] 0 1 0 … 0 S 1 [0] … 1 S 4 [0] 1 0 S 2 … 01 [0] S 5 [0] 1 0 S 3 [1] 1 0 0 S 6 [0] … 010 Real Time Embedded … 100 Systems 0, 1

Finite State Machine Word Problems Finite String Recognizer S 2, S 5 with incomplete transitions S 2 = … 01; If next input is 1, then string could be prefix of (01)1(00) S 4 handles just this case! S 5 = … 10; If next input is 1, then string could be prefix of (10)1(0) S 2 handles just this case! Real Time Embedded Systems

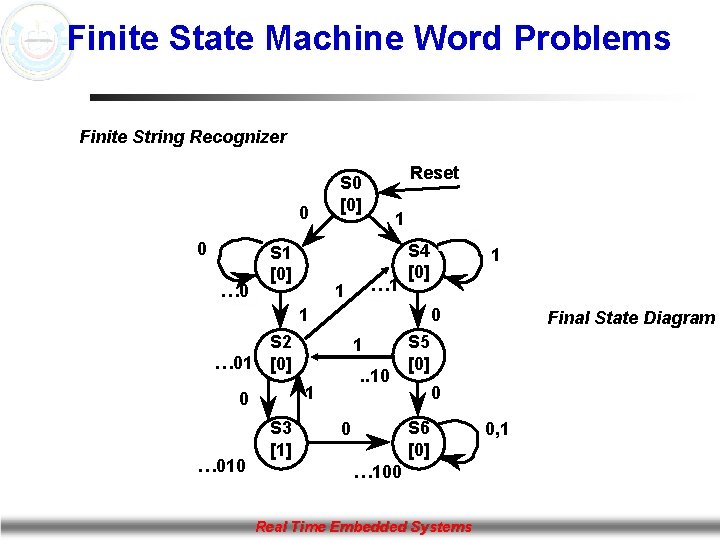
Finite State Machine Word Problems Finite String Recognizer 0 0 … 0 S 1 [0] Reset S 0 [0] 1 … 1 1 S 4 [0] 1 0 S 2 … 01 [0] … 010 1. . 10 1 0 S 3 [1] 1 S 5 [0] 0 S 6 [0] 0 Final State Diagram … 100 Real Time Embedded Systems 0, 1

FSM Design n Six Step Process 1. Understand the statement of the Specification. 2. Obtain an abstract specification of the Synchronous Sequential Circuits (SSC). 3. Generate State Table. 4. Perform state minimization. 5. Choose FF types to implement SSC state register. 6. Implement the SSC. Real Time Embedded Systems

Vending Machine Example Real Time Embedded Systems

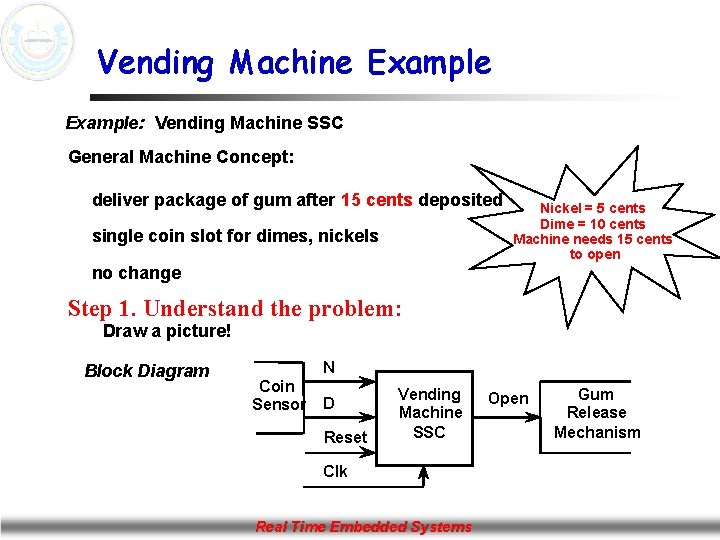
Vending Machine Example: Vending Machine SSC General Machine Concept: deliver package of gum after 15 cents deposited single coin slot for dimes, nickels Nickel = 5 cents Dime = 10 cents Machine needs 15 cents to open no change Step 1. Understand the problem: Draw a picture! Block Diagram N Coin Sensor D Reset Vending Machine SSC Clk Real Time Embedded Systems Open Gum Release Mechanism

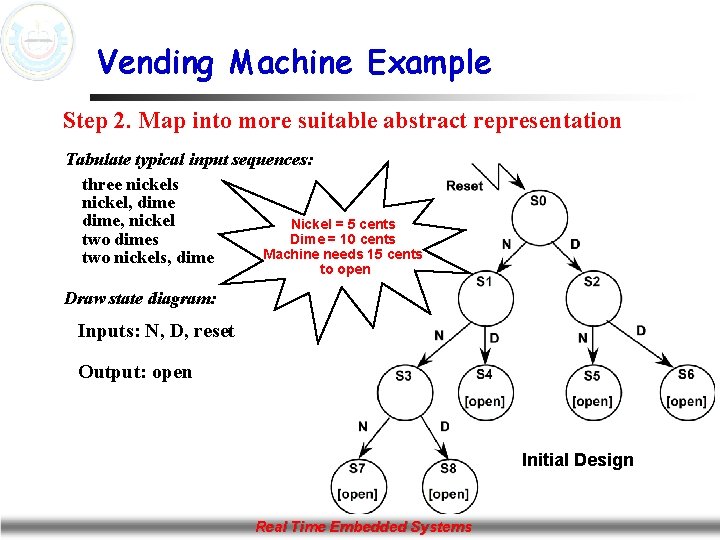
Vending Machine Example Step 2. Map into more suitable abstract representation Tabulate typical input sequences: three nickels nickel, dime, nickel Nickel = 5 cents Dime = 10 cents two dimes Machine needs 15 cents two nickels, dime to open Draw state diagram: Inputs: N, D, reset Output: open Initial Design Real Time Embedded Systems

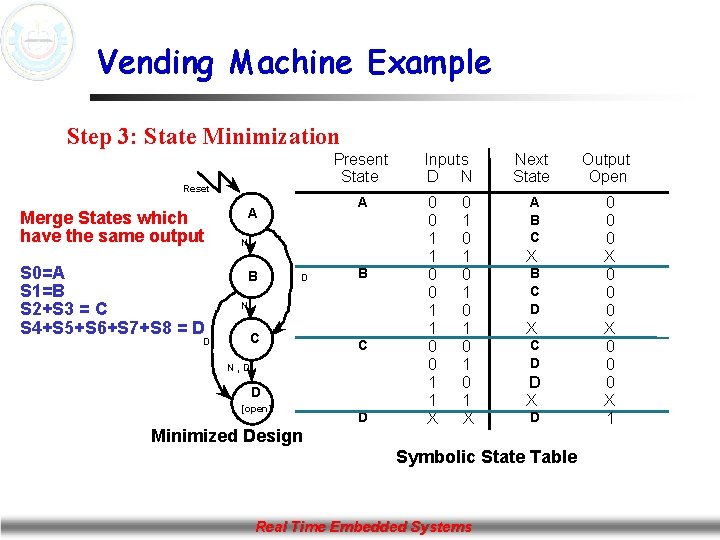
Vending Machine Example Step 3: State Minimization Present State Reset Merge States which have the same output S 0=A S 1=B S 2+S 3 = C S 4+S 5+S 6+S 7+S 8 = D D A A N B D B N C C N, D D [open] Minimized Design D Inputs D N 0 0 1 1 X 0 1 0 1 0 1 X Next State Output Open A B C 0 0 0 X 1 X B C D X C D D X D Symbolic State Table Real Time Embedded Systems

Vending Machine Example Step 4: State Encoding State Present State Q 1 Q 0 0 0 A 0 1 1 B C D Inputs D N 0 0 1 1 0 1 0 1 D 1 D 0 Next State Q 1+ Q+0 Output Open 0 0 0 1 1 0 X X 0 1 1 X X 1 1 1 X X 0 0 0 X 1 1 1 X Real Time Embedded Systems NOTE! For D-FFs the next state will be what is at the D input.

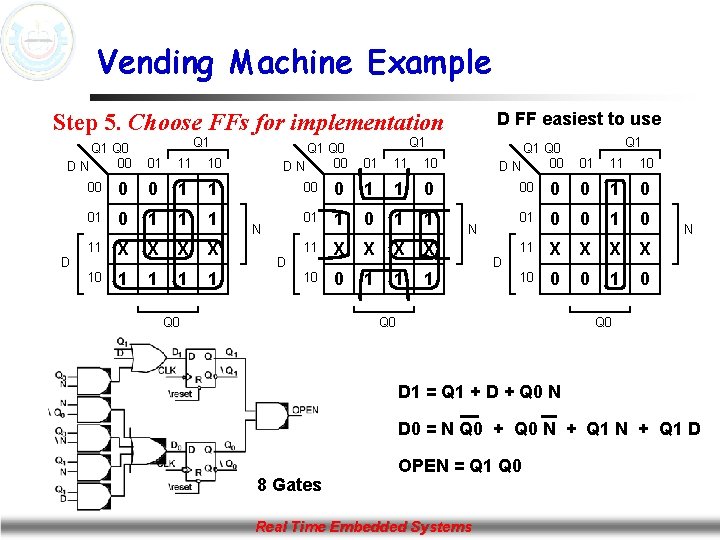
Vending Machine Example Step 5. Choose FFs for implementation Q 1 Q 0 00 DN D Q 1 01 11 10 00 0 0 1 1 01 0 1 11 X X 1 1 10 Q 1 Q 0 00 DN N D Q 1 01 11 10 00 0 1 1 0 01 1 0 1 1 11 X X 0 1 10 Q 0 D FF easiest to use Q 1 Q 0 00 DN N D Q 1 01 11 10 00 0 0 1 0 11 X X 10 0 0 1 0 Q 0 N Q 0 D 1 = Q 1 + D + Q 0 N D 0 = N Q 0 + Q 0 N + Q 1 D 8 Gates OPEN = Q 1 Q 0 Real Time Embedded Systems

VHDL Design of State Machines Real Time Embedded Systems

FSM minimization n Four steps for FSM minimization example. Present State Inputs X=a X=b X=c A B C D E F E, 1 C, 0 B, 1 C, 0 A, 0 C, 0 F, 1 A, 0 F, 1 E, 1 B, 1 E, 1 D, 1 E, 1 B, 1 C, 1 Next state , output Step(1) Generate groups of states that generate the same output. This is called portions 1. P 1 = ( A, C) (B, D, E, F) Real Time Embedded Systems

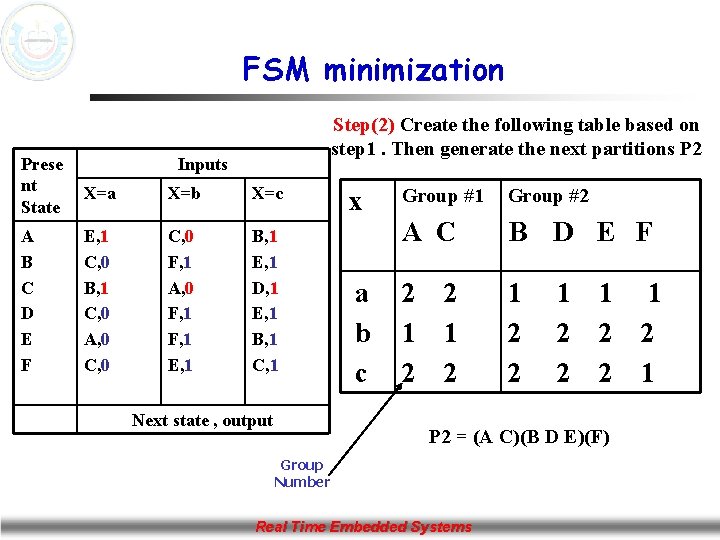
FSM minimization Step(2) Create the following table based on step 1. Then generate the next partitions P 2 Prese nt State Inputs X=a X=b X=c A B C D E F E, 1 C, 0 B, 1 C, 0 A, 0 C, 0 F, 1 A, 0 F, 1 E, 1 B, 1 E, 1 D, 1 E, 1 B, 1 C, 1 Next state , output x a b c Group #1 Group #2 A C B D E F 2 1 2 1 2 2 P 2 = (A C)(B D E)(F) Group Number Real Time Embedded Systems 1 2 1

FSM minimization Step(3) Create the following table based on step 2. Then generate the next partitions P 3 Prese nt State Inputs X=a X=b X=c A B C D E F E, 1 C, 0 B, 1 C, 0 A, 0 C, 0 F, 1 A, 0 F, 1 E, 1 B, 1 E, 1 D, 1 E, 1 B, 1 C, 1 x Group #1 Group #2 A C B D 1 1 3 3 2 2 a 2 b 1 c Next state , output Note: P 2 = P 3 then stop partitions and go to step 4 2 2 1 2 Group #3 E 1 3 2 F 1 2 1 P 3 = (A C)(B D E)(F) = P 2 Real Time Embedded Systems

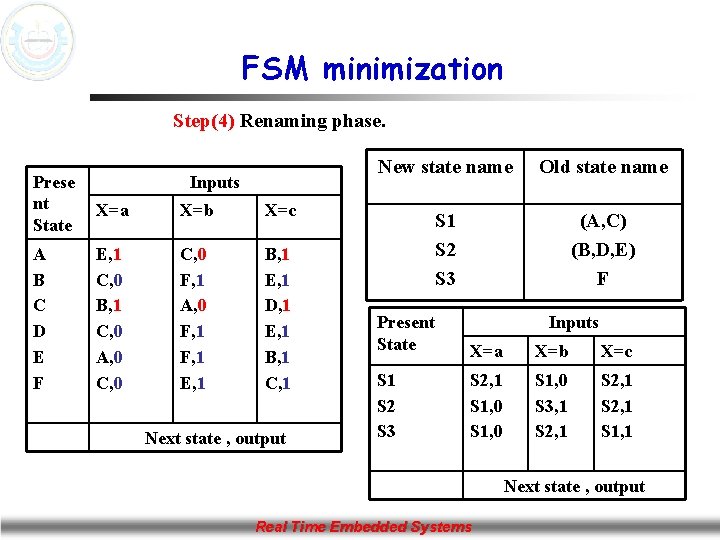
FSM minimization Step(4) Renaming phase. Prese nt State Inputs X=a X=b X=c A B C D E F E, 1 C, 0 B, 1 C, 0 A, 0 C, 0 F, 1 A, 0 F, 1 E, 1 B, 1 E, 1 D, 1 E, 1 B, 1 C, 1 Next state , output New state name Old state name S 1 S 2 S 3 (A, C) (B, D, E) F Present State Inputs X=a X=b X=c S 1 S 2 S 3 S 2, 1 S 1, 0 S 3, 1 S 2, 1 S 1, 1 Next state , output Real Time Embedded Systems

Case Study: FSMD: finite-state machine with datapath Example : ( greatest common divisor ) (a) black-box view go_i x_i y_i GCD d_o Steps : n n First create algorithm Convert algorithm to “complex” state machine n Known as FSMD: finitestate machine with datapath (c) state diagram (b) desired functionality 0: int x, y; 1: while (1) { 2: while (!go_i); 3: x = x_i; 4: y = y_i; 5: while (x != y) { 6: if (x < y) 7: y = y - x; else 8: x = x - y; } 9: d_o = x; } 1 !(!go_i) 2: !go_i 2 -J: 3: x = x_i 4: y = y_i !(x!=y) 5: x!=y 6: x<y 7: y = y -x 8: 6 -J: 5 -J: 9: 1 -J: Real Time Embedded Systems !1 1: d_o = x !(x<y) x=x-y

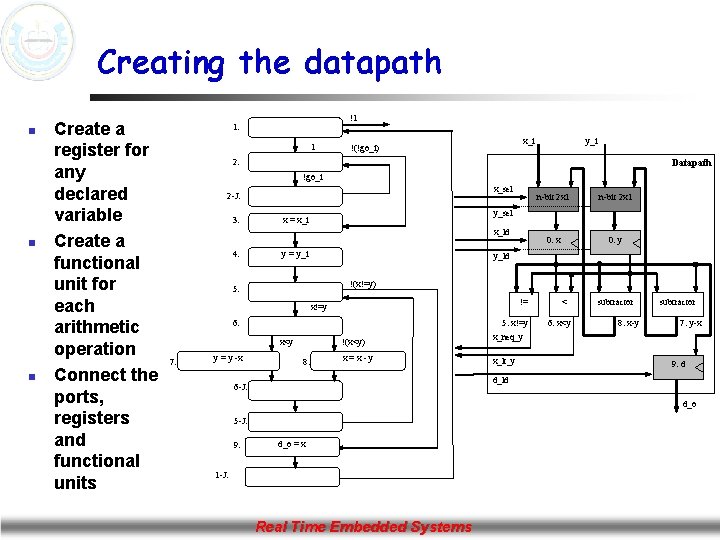
Creating the datapath n n n Create a register for any declared variable Create a functional unit for each arithmetic operation Connect the ports, registers and functional units !1 1: 1 x_i !(!go_i) y_i 2: Datapath !go_i x_sel 2 -J: 3: y = y_i 0: y !(x!=y) != x!=y 5: x!=y 6: x<y y = y -x 0: x y_ld 5: 7: n-bit 2 x 1 y_sel x = x_i x_ld 4: n-bit 2 x 1 !(x<y) 8: x=x-y < 6: x<y subtractor 8: x-y subtractor 7: y-x x_neq_y x_lt_y 9: d d_ld 6 -J: d_o 5 -J: 9: d_o = x 1 -J: Real Time Embedded Systems

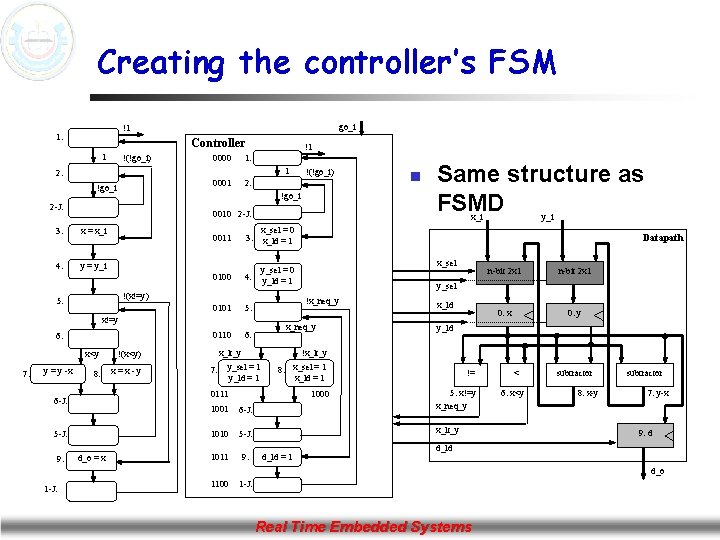
Creating the controller’s FSM go_i !1 1: Controller 1 !(!go_i) !1 0000 1: 0001 2: !go_i 2 -J: 0010 2 -J: 3: x = x_i 4: y = y_i x_sel = 0 x_ld = 1 0100 4: y_sel = 0 y_ld = 1 0101 5: 0110 6: !(x!=y) y = y -x x<y !(x<y) 8: x=x-y 5 -J: 9: x_lt_y 7: y_sel = 1 y_ld = 1 d_o = x 1001 6 -J: 1010 5 -J: 1011 9: 1100 1 -J: x_sel y_i n-bit 2 x 1 0: x 0: y y_sel x_neq_y x_ld y_ld !x_lt_y x_sel =1 8: x_ld = 1 != 1000 5: x!=y 0111 6 -J: Same structure as FSMD Datapath !x_neq_y x!=y 6: n x_i 3: 0011 5: 7: !(!go_i) < 6: x<y subtractor 8: x-y subtractor 7: y-x x_neq_y x_lt_y d_ld = 1 9: d d_ld d_o 1 -J: Real Time Embedded Systems

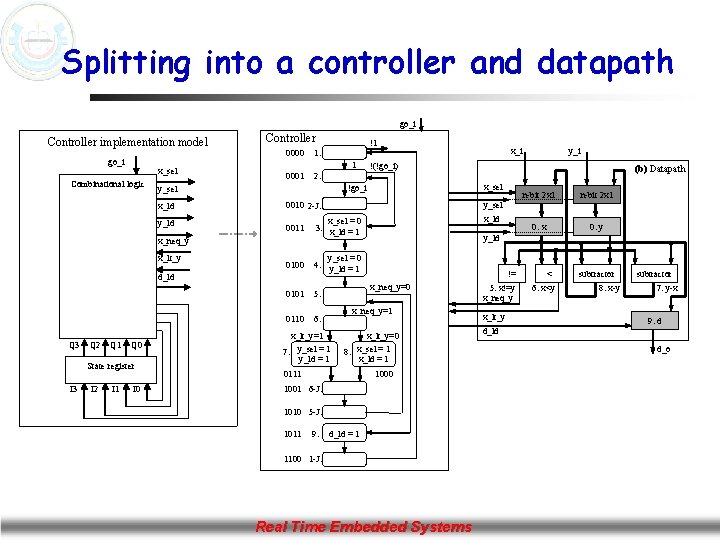
Splitting into a controller and datapath go_i Controller implementation model go_i x_sel Combinational logic Controller 0000 1 0001 0010 2 -J: y_ld 0011 0100 d_ld Q 1 Q 0 State register I 3 I 2 I 1 I 0 0110 6: x_ld n-bit 2 x 1 0: x 0: y y_ld != x_neq_y=0 x_neq_y=1 x_lt_y=1 7: y_sel = 1 y_ld = 1 x_lt_y=0 x_sel =1 8: x_ld = 1 0111 1000 1001 6 -J: 1010 5 -J: 9: n-bit 2 x 1 y_sel = 0 4: y_ld = 1 5: y_i (b) Datapath x_sel = 0 3: x_ld = 1 0101 1011 x_i !(!go_i) !go_i x_ld x_lt_y Q 2 2: y_sel x_neq_y Q 3 !1 1: d_ld = 1 1100 1 -J: Real Time Embedded Systems 5: x!=y x_neq_y x_lt_y < 6: x<y subtractor 8: x-y subtractor 7: y-x 9: d d_ld d_o

Optimizing the FSMD n Areas of possible improvements n merge states n n states with constants on transitions can be eliminated, transition taken is already known states with independent operations can be merged Real Time Embedded Systems

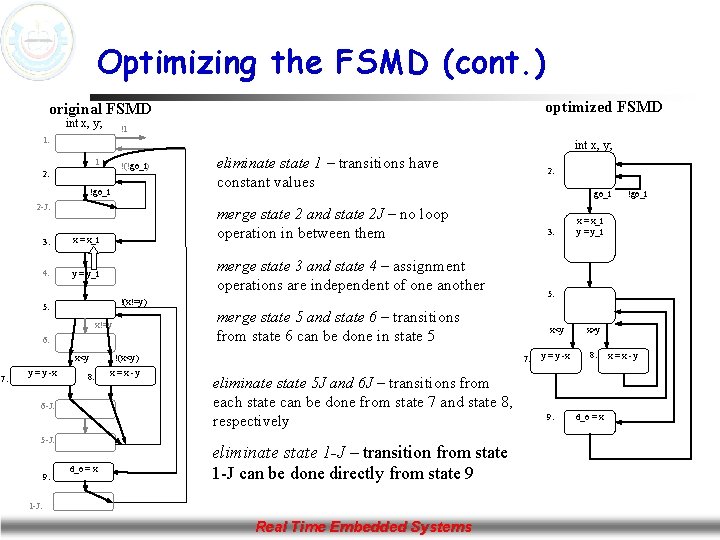
Optimizing the FSMD (cont. ) optimized FSMD original FSMD int x, y; !1 1: int x, y; 1 !(!go_i) 2: !go_i 2 -J: 3: x = x_i 4: y = y_i 3: x<y merge state 5 and state 6 – transitions from state 6 can be done in state 5 8: 6 -J: 5 -J: d_o = x !(x<y) x=x-y 7: eliminate state 5 J and 6 J – transitions from each state can be done from state 7 and state 8, respectively eliminate state 1 -J – transition from state 1 -J can be done directly from state 9 1 -J: Real Time Embedded Systems !go_i x = x_i y = y_i 5: !(x!=y) 6: 9: go_i merge state 3 and state 4 – assignment operations are independent of one another x!=y y = y -x 2: merge state 2 and state 2 J – no loop operation in between them 5: 7: eliminate state 1 – transitions have constant values x<y x>y y = y -x 8: 9: d_o = x x=x-y

Optimizing the datapath n Sharing of functional units n n if same operation occurs in different states, they can share a single functional unit Multi-functional units n ALUs support a variety of operations, it can be shared among operations occurring in different states Real Time Embedded Systems

Optimizing the FSM n State minimization (As Discussed n Previously) task of merging equivalent states into a single state n state equivalent if for all possible input combinations the two states generate the same outputs and transitions to the next same state Real Time Embedded Systems

References n n n “Embedded Systems Design: A Unified Hardware/Software Introduction” Book Slides. Frank Vahid, Tony Givarrgis, Wiley, 2002 www. mwnl. snu. ac. kr/~schoi/Courses/201/Course_Mater ials “Digital Design with CPLD Applications & VHDL” Book, Dueck , 2005 http: //en. wikipedia. org/wiki/Finite_state_machine#Conce pts_and_vocabulary “Advanced Topic on Sequential Logic Design” handout. Real Time Embedded Systems