Finite State Machines FSM n Sequential circuits q

Finite State Machines (FSM) n Sequential circuits q q n Models for representing sequential circuits q n q shift registers counters Design procedure q q q n finite-state machines (Moore and Mealy) Basic sequential circuits revisited q n primitive sequential elements combinational logic state diagrams state transition table next state functions Hardware description languages (HDL) 1

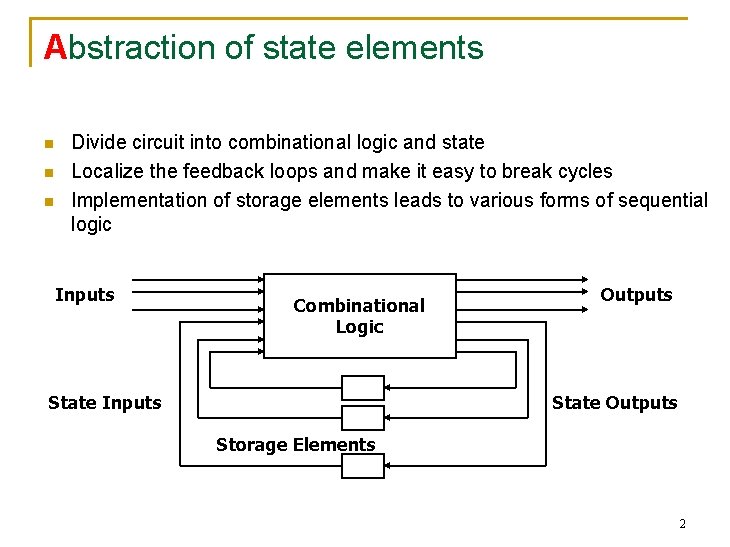
Abstraction of state elements n n n Divide circuit into combinational logic and state Localize the feedback loops and make it easy to break cycles Implementation of storage elements leads to various forms of sequential logic Inputs Combinational Logic State Inputs Outputs State Outputs Storage Elements 2

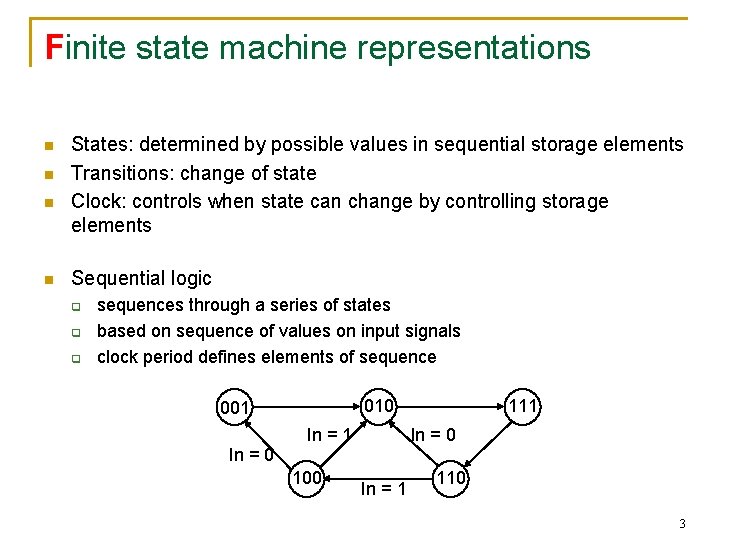
Finite state machine representations n n States: determined by possible values in sequential storage elements Transitions: change of state Clock: controls when state can change by controlling storage elements Sequential logic q q q sequences through a series of states based on sequence of values on input signals clock period defines elements of sequence 010 001 In = 0 In = 1 100 111 In = 0 In = 1 110 3

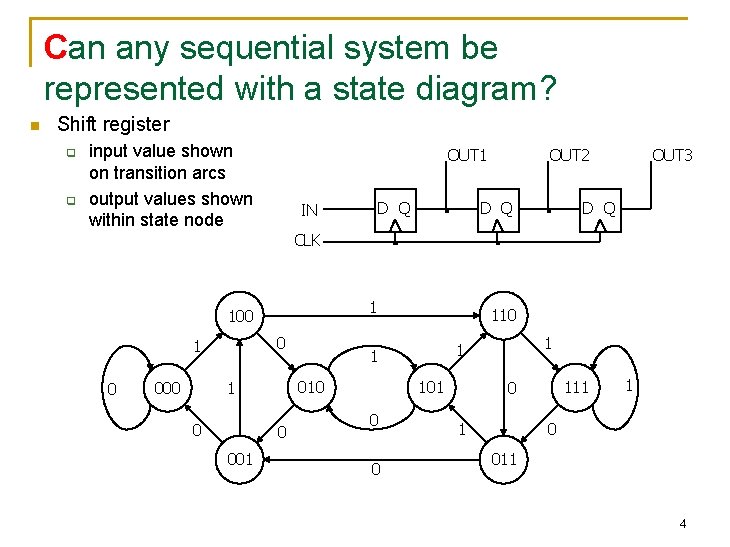
Can any sequential system be represented with a state diagram? n Shift register q q input value shown on transition arcs output values shown within state node OUT 1 IN D Q OUT 2 D Q OUT 3 D Q CLK 1 100 0 1 0 001 101 0 0 1 1 1 010 1 000 111 0 1 1 0 011 4

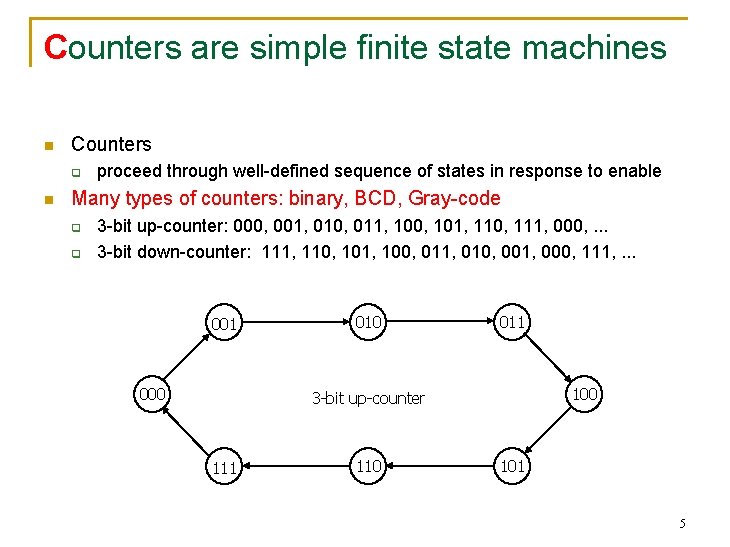
Counters are simple finite state machines n Counters q n proceed through well-defined sequence of states in response to enable Many types of counters: binary, BCD, Gray-code q q 3 -bit up-counter: 000, 001, 010, 011, 100, 101, 110, 111, 000, . . . 3 -bit down-counter: 111, 110, 101, 100, 011, 010, 001, 000, 111, . . . 001 000 011 100 3 -bit up-counter 111 110 101 5

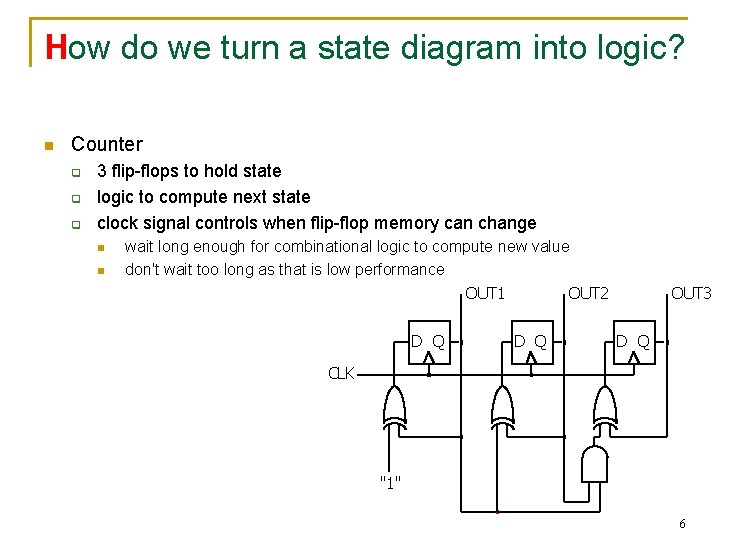
How do we turn a state diagram into logic? n Counter q q q 3 flip-flops to hold state logic to compute next state clock signal controls when flip-flop memory can change n n wait long enough for combinational logic to compute new value don't wait too long as that is low performance OUT 1 OUT 2 D Q OUT 3 D Q CLK "1" 6

FSM design procedure n Start with counters q q n State diagram to state transition table q q n tabular form of state diagram like a truth-table State encoding q q n simple because output is just state simple because no choice of next state based on input decide on representation of states for counters it is simple: just its value Implementation q q flip-flop for each state bit combinational logic based on encoding

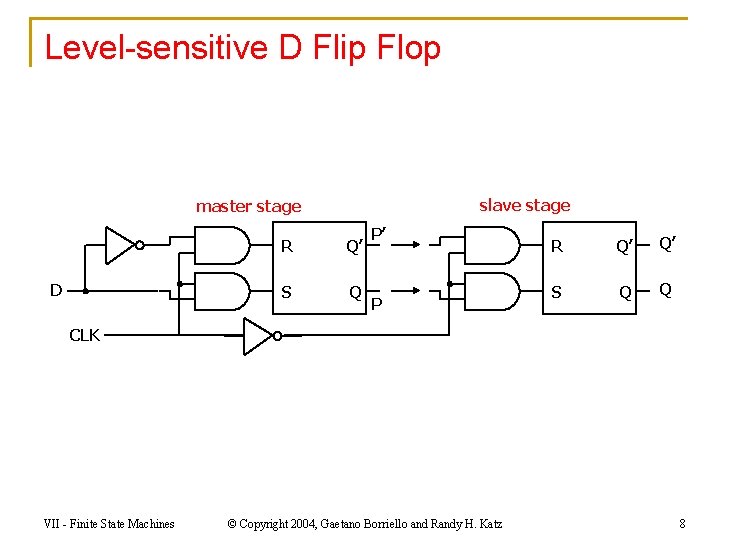
Level-sensitive D Flip Flop slave stage master stage D R Q’ S Q P’ P R Q’ Q’ S Q Q CLK VII - Finite State Machines © Copyright 2004, Gaetano Borriello and Randy H. Katz 8

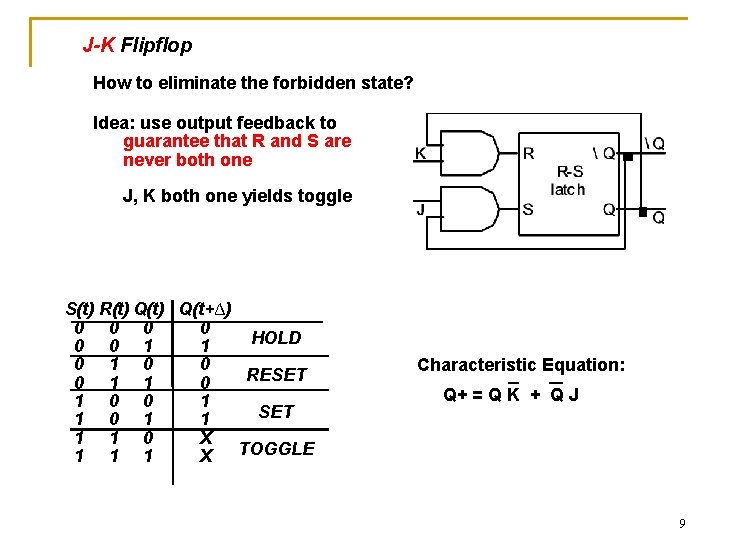
J-K Flipflop How to eliminate the forbidden state? Idea: use output feedback to guarantee that R and S are never both one J, K both one yields toggle S(t) R(t) Q(t+∆) 0 0 HOLD 0 0 1 1 0 0 RESET 0 1 1 0 0 1 SET 1 0 1 1 0 X TOGGLE 1 1 1 X Characteristic Equation: Q+ = Q K + Q J 9

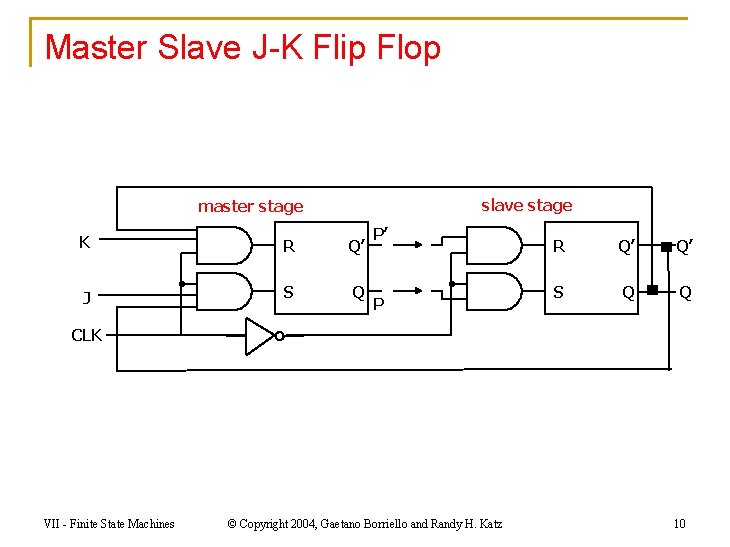
Master Slave J-K Flip Flop slave stage master stage K R Q’ J S Q P’ P R Q’ Q’ S Q Q CLK VII - Finite State Machines © Copyright 2004, Gaetano Borriello and Randy H. Katz 10

Choosing a Flipflop R-S Clocked Latch: used as storage element in narrow width clocked systems its use is not recommended! however, fundamental building block of other flipflop types J-K Flipflop: versatile building block can be used to implement D and T FFs usually requires least amount of logic to implement ƒ(In, Q, Q+) but has two inputs with increased wiring complexity because of 1's catching, never use master/slave J-K FFs edge-triggered varieties exist D Flipflop: minimizes wires, much preferred in VLSI technologies simplest design technique best choice for storage registers T Flipflops: don't really exist, constructed from J-K FFs usually best choice for implementing counters Preset and Clear inputs highly desirable!! 11

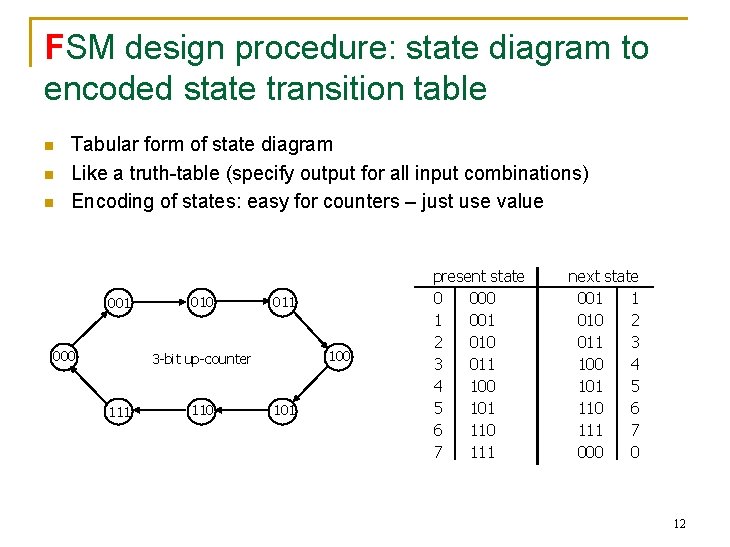
FSM design procedure: state diagram to encoded state transition table n n n Tabular form of state diagram Like a truth-table (specify output for all input combinations) Encoding of states: easy for counters – just use value 001 000 011 100 3 -bit up-counter 111 110 101 present state 0 000 1 001 2 010 3 011 4 100 5 101 6 110 7 111 next state 001 1 010 2 011 3 100 4 101 5 110 6 111 7 000 0 12

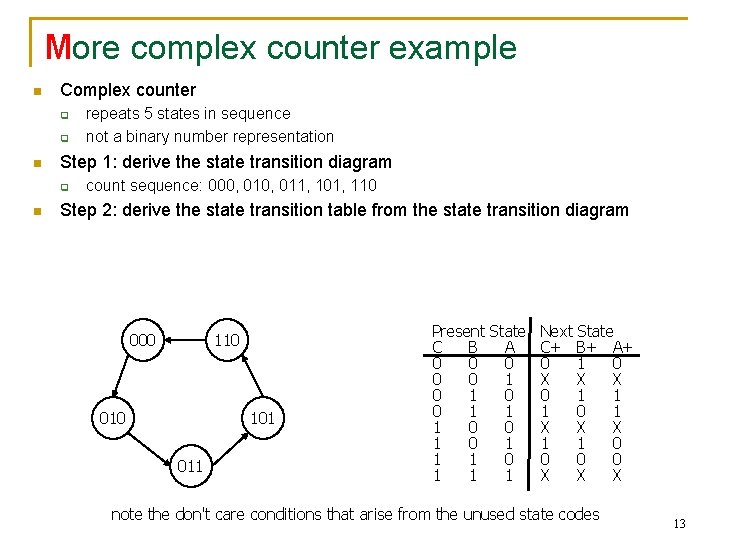
More complex counter example n Complex counter q q n Step 1: derive the state transition diagram q n repeats 5 states in sequence not a binary number representation count sequence: 000, 011, 101, 110 Step 2: derive the state transition table from the state transition diagram 000 110 010 101 011 Present State Next State C B A C+ B+ A+ 0 0 1 0 0 0 1 X X X 0 1 0 0 1 1 1 0 0 X X X 1 0 1 1 0 0 1 1 1 X X X note the don't care conditions that arise from the unused state codes 13

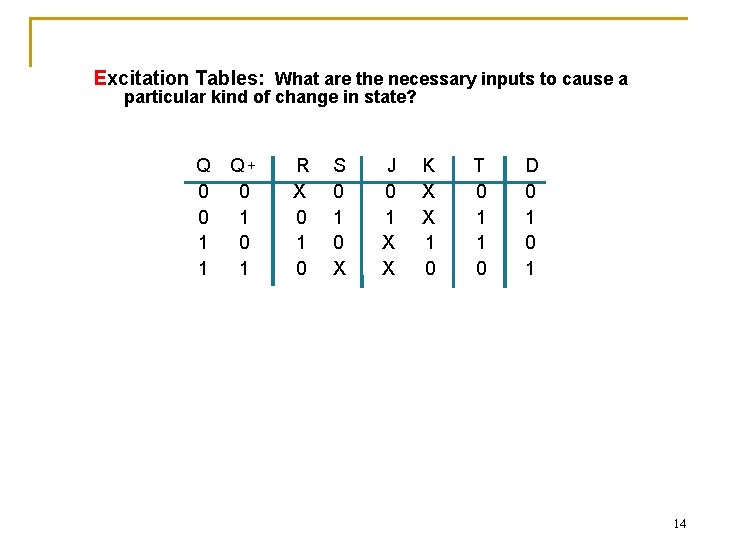
Excitation Tables: What are the necessary inputs to cause a particular kind of change in state? Q 0 0 1 1 Q+ 0 1 R X 0 1 0 S 0 1 0 X J 0 1 X X K X X 1 0 T 0 1 1 0 D 0 1 14

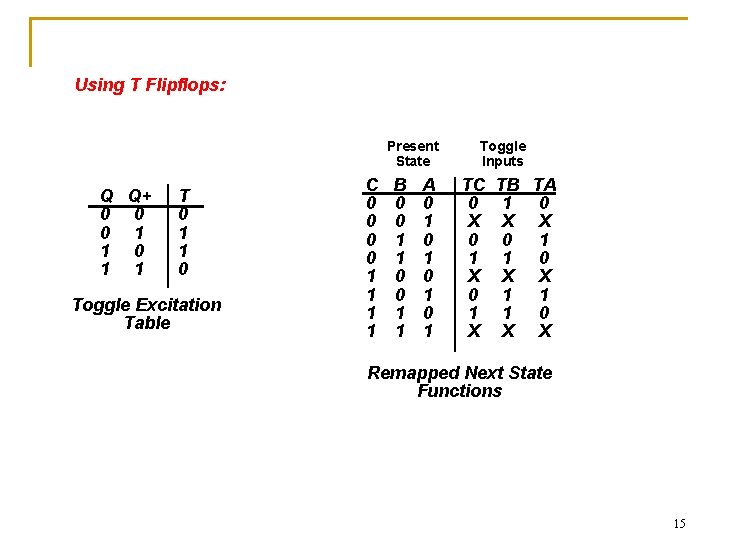
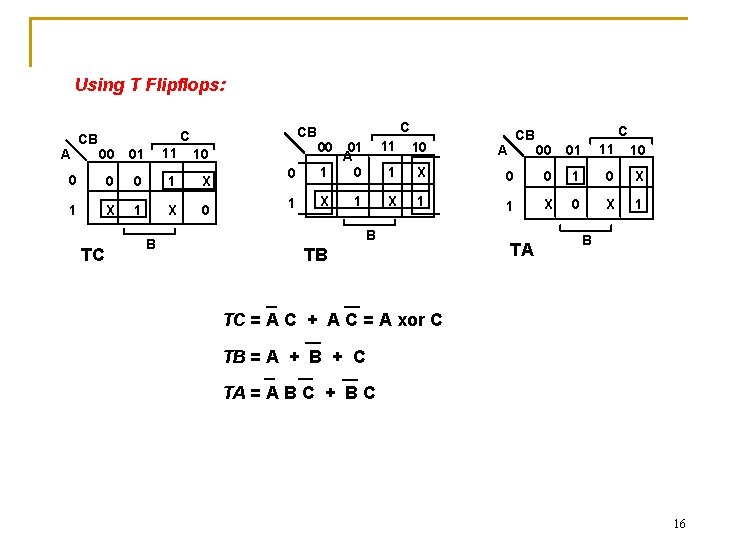
Using T Flipflops: Present State Q Q+ 0 0 0 1 1 T 0 1 1 0 Toggle Excitation Table C 0 0 1 1 B 0 0 1 1 A 0 1 0 1 Toggle Inputs TC 0 X 0 1 X TB TA 1 0 X X 0 1 1 0 X X 1 1 1 0 X X Remapped Next State Functions 15

Using T Flipflops: CB CB C 00 01 11 10 0 1 X 1 X 0 A TC B C 00 0 1 01 A 0 1 X 1 11 10 1 X X 1 B TB CB C 00 01 11 10 0 0 1 0 X 1 X 0 X 1 A TA B TC = A C + A C = A xor C TB = A + B + C TA = A B C + B C 16

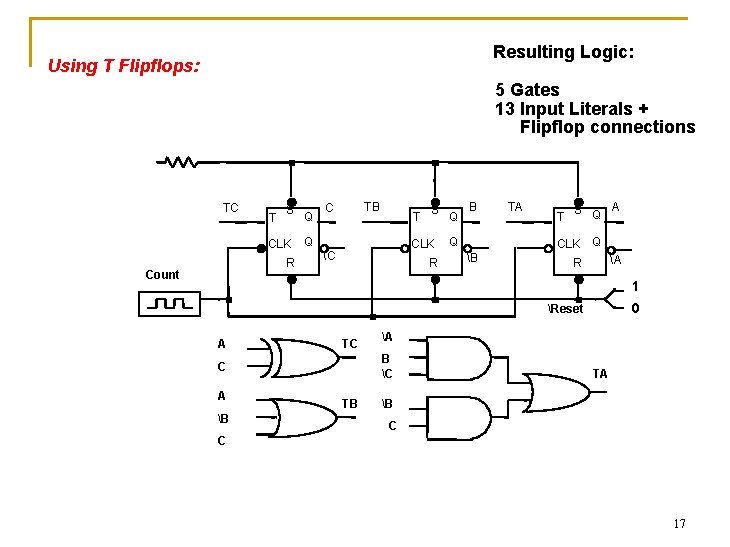
Resulting Logic: Using T Flipflops: 5 Gates 13 Input Literals + Flipflop connections TC T S CLK R Count Q TB C T Q S CLK C R Q B Q TA T S Q A CLK B Q A R 1 0 Reset A TC B C C A B A TB TA B C C 17

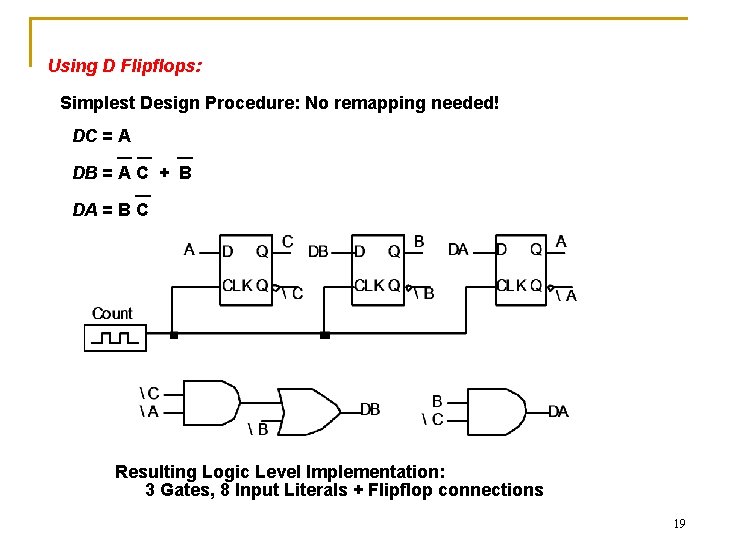
Using D Flipflops: Q Q+ 0 0 0 1 1 D 0 1 Excitation Table Present State Next State C B A C+ B+ A+ 0 0 1 0 0 0 1 X X X 0 1 0 0 1 1 1 0 0 X X X 1 0 1 1 0 0 1 1 1 X X X D Inputs DC DB 0 1 X X 0 1 1 0 X X 1 1 0 0 X X DA 0 X 1 1 X 0 0 X Remapped Next State Functions 18

Using D Flipflops: Simplest Design Procedure: No remapping needed! DC = A DB = A C + B DA = B C Resulting Logic Level Implementation: 3 Gates, 8 Input Literals + Flipflop connections 19

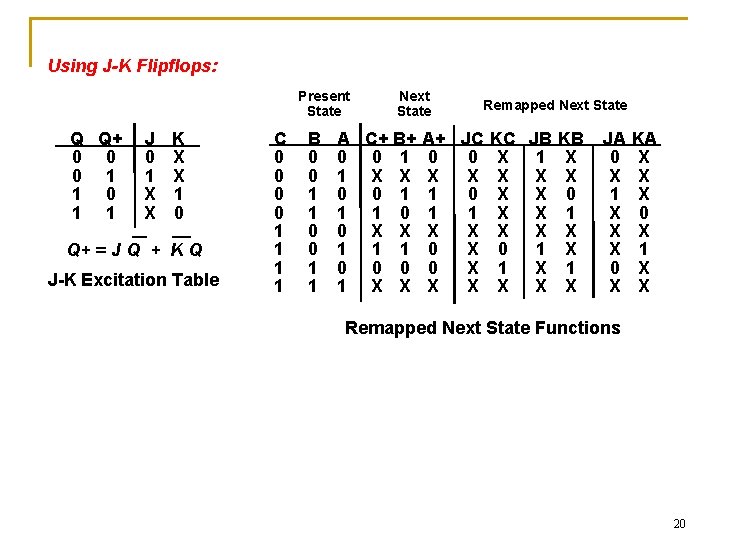
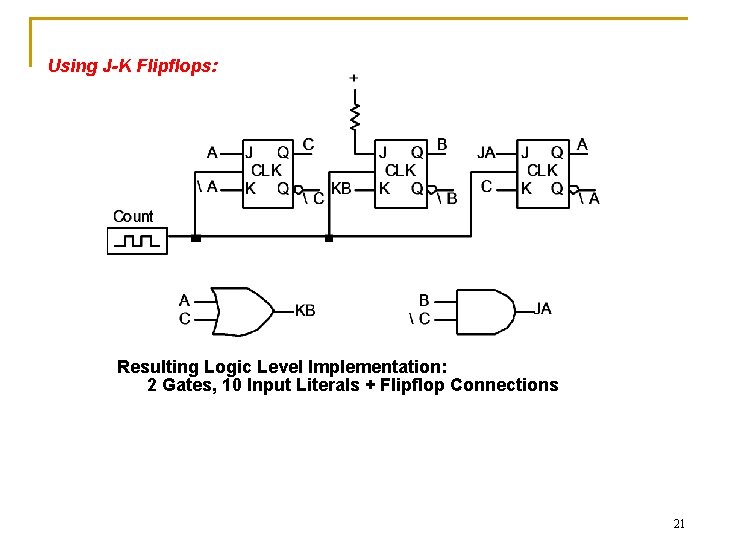
Using J-K Flipflops: Present State Q Q+ 0 0 0 1 1 J 0 1 X X K X X 1 0 Q+ = J Q + K Q J-K Excitation Table C 0 0 1 1 B 0 0 1 1 Next State Remapped Next State A C+ B+ A+ JC KC JB KB 0 0 1 0 0 X 1 X X X X 0 0 1 1 0 X X 0 1 1 X X 1 0 X X X X 1 1 1 0 X 0 1 X 0 0 X 1 1 X X X X JA KA 0 X X X 1 X X 0 X X X 1 0 X X X Remapped Next State Functions 20

Using J-K Flipflops: Resulting Logic Level Implementation: 2 Gates, 10 Input Literals + Flipflop Connections 21

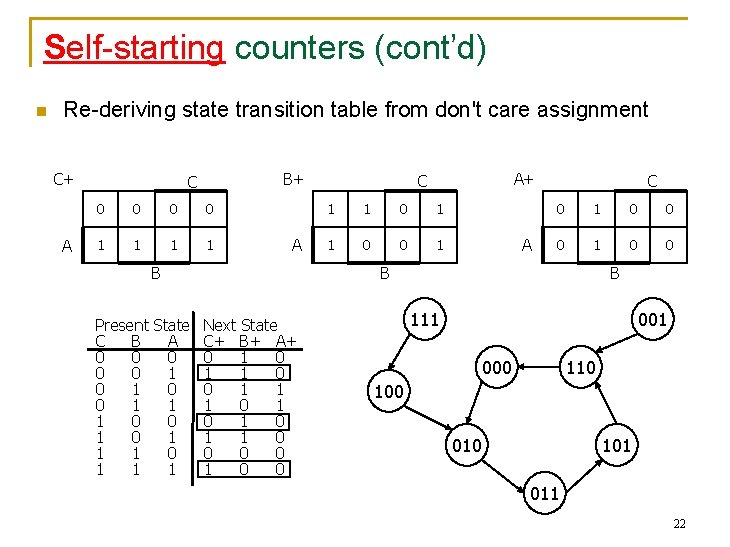
Self-starting counters (cont’d) n Re-deriving state transition table from don't care assignment C+ A B+ C 0 0 1 1 A B Present State Next State C B A C+ B+ A+ 0 0 1 0 0 0 1 1 1 0 0 1 1 0 0 0 1 0 1 1 1 0 0 0 0 1 1 0 0 A+ C 1 1 0 0 1 A C 0 1 0 0 B B 001 111 000 110 100 010 101 011 22

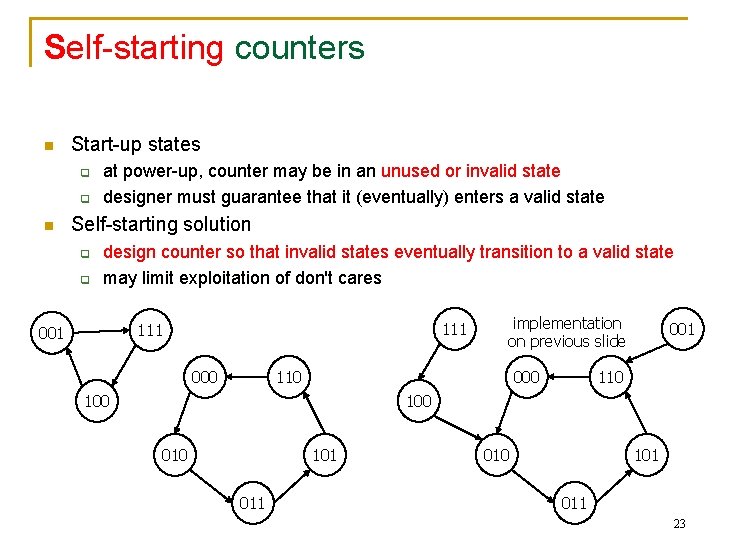
Self-starting counters n Start-up states q q n at power-up, counter may be in an unused or invalid state designer must guarantee that it (eventually) enters a valid state Self-starting solution q q design counter so that invalid states eventually transition to a valid state may limit exploitation of don't cares 111 001 000 implementation on previous slide 000 110 001 110 100 010 101 011 23

Comparison of Mealy and Moore machines Mealy machines tend to have less states n q n Moore machines are safer to use q q n different outputs on arcs (n 2) rather than states (n) outputs change at clock edge (always one cycle later) in Mealy machines, input change can cause output change as soon as logic is done – a big problem when two machines are interconnected – asynchronous feedback may occur if one isn’t careful Mealy machines react faster to inputs q q react in same cycle – don't need to wait for clock in Moore machines, more logic may be necessary to decode state into outputs – more gate delays after clock edge 24

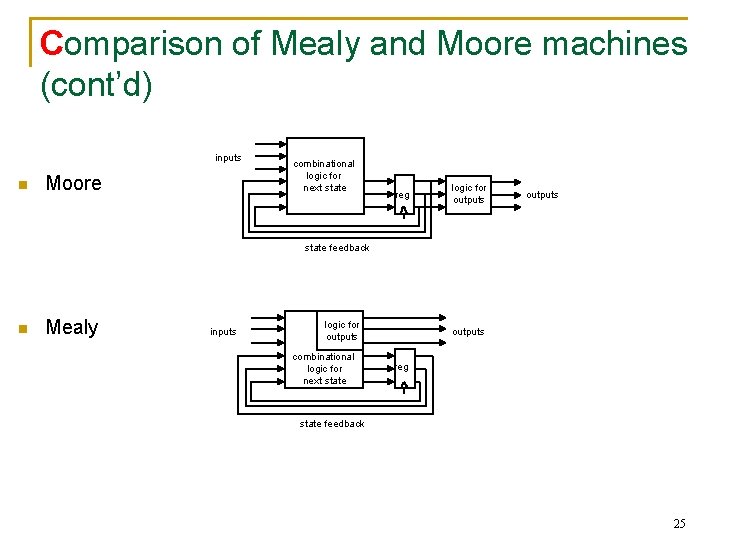
Comparison of Mealy and Moore machines (cont’d) inputs n Moore combinational logic for next state reg logic for outputs state feedback n Mealy inputs logic for outputs combinational logic for next state outputs reg state feedback 25

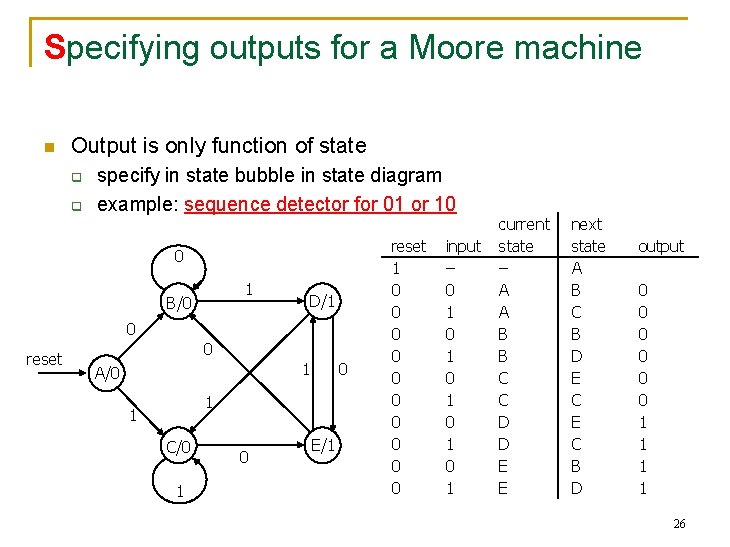
Specifying outputs for a Moore machine n Output is only function of state q q specify in state bubble in state diagram example: sequence detector for 01 or 10 0 1 B/0 D/1 0 reset 0 1 A/0 0 1 1 C/0 1 0 E/1 reset 1 0 0 0 0 0 input – 0 1 0 1 0 1 current state – A A B B C C D D E E next state A B C B D E C B D output 0 0 0 1 1 26

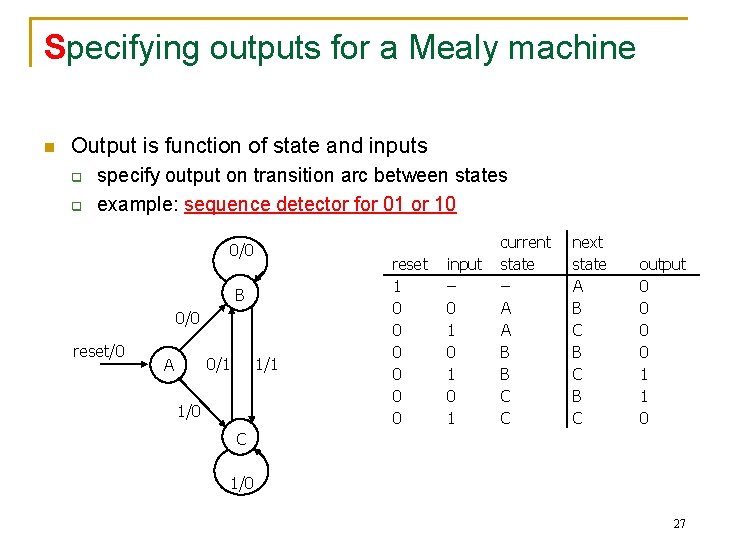
Specifying outputs for a Mealy machine n Output is function of state and inputs q q specify output on transition arc between states example: sequence detector for 01 or 10 0/0 B 0/0 reset/0 0/1 A 1/1 1/0 reset 1 0 0 0 input – 0 1 0 1 current state – A A B B C C next state A B C B C output 0 0 1 1 0 C 1/0 27

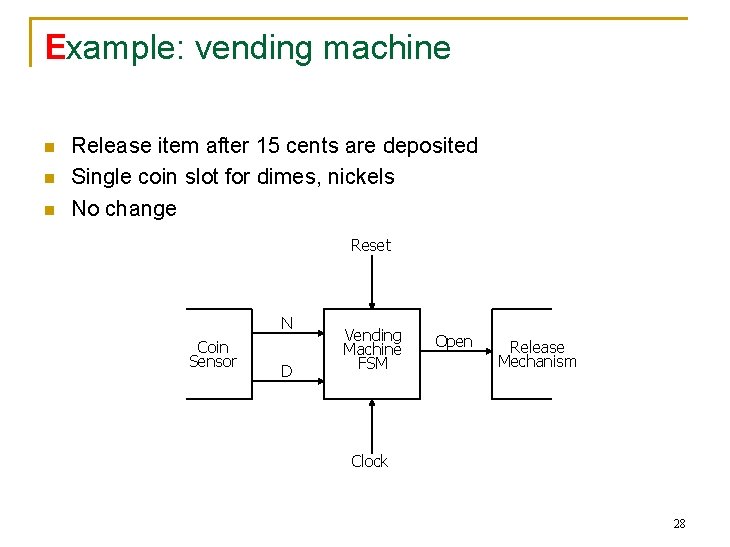
Example: vending machine n n n Release item after 15 cents are deposited Single coin slot for dimes, nickels No change Reset N Coin Sensor D Vending Machine FSM Open Release Mechanism Clock 28

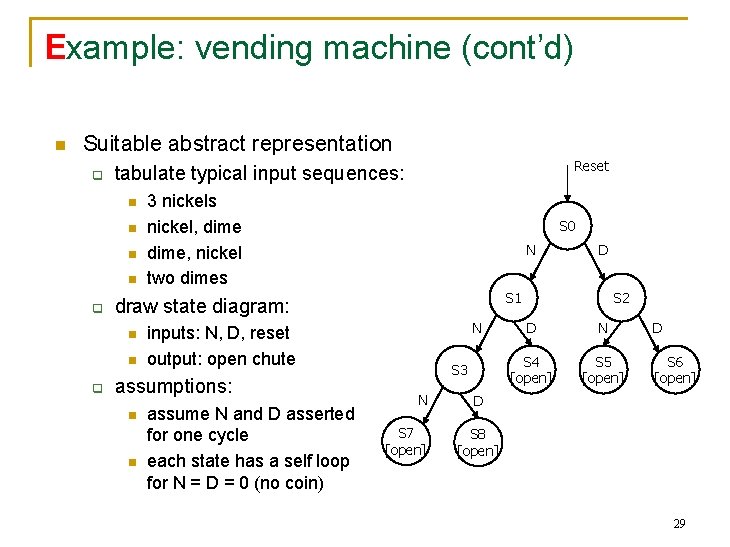
Example: vending machine (cont’d) n Suitable abstract representation q n n q 3 nickels nickel, dime, nickel two dimes S 0 N n n n N inputs: N, D, reset output: open chute assumptions: assume N and D asserted for one cycle each state has a self loop for N = D = 0 (no coin) D S 1 draw state diagram: n q Reset tabulate typical input sequences: S 3 N S 7 [open] S 2 D N S 4 [open] S 5 [open] D S 6 [open] D S 8 [open] 29

Example: vending machine (cont’d) n Minimize number of states - reuse states whenever possible present state 0¢ Reset 0¢ 5¢ N D D 10¢ N+D 15¢ [open] 15¢ inputs D N 0 0 0 1 1 0 0 0 1 1 – – next state 0¢ 5¢ 10¢ – 5¢ 10¢ 15¢ – 15¢ output open 0 0 0 – 1 symbolic state table 30

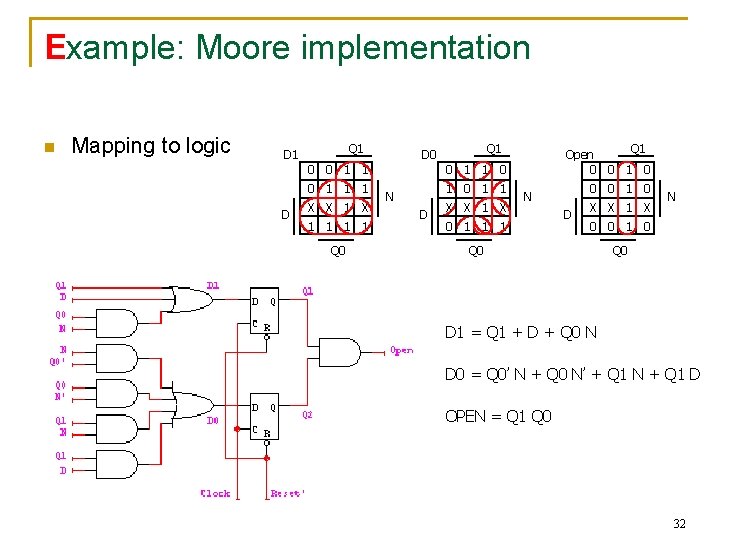
Example: vending machine (cont’d) n Uniquely encode states present state inputs Q 1 Q 0 D N 0 0 0 1 1 0 1 0 0 0 1 1 1 0 0 1 1 – – next D 1 0 0 1 – 0 1 1 – 1 state D 0 0 1 0 – 1 0 1 – 0 1 1 – 1 output open 0 0 0 – 1 31

Example: Moore implementation n Mapping to logic Q 1 D 1 0 0 1 1 1 D X X 1 1 1 1 Q 0 Q 1 D 0 Q 1 Open 0 0 1 1 N D X X 1 X 0 0 1 0 N 0 1 1 1 D X X 1 X N 0 0 1 0 Q 0 D 1 = Q 1 + D + Q 0 N D 0 = Q 0’ N + Q 0 N’ + Q 1 N + Q 1 D OPEN = Q 1 Q 0 32

Example: vending machine (cont’d) n One-hot encoding present state Q 3 Q 2 Q 1 Q 0 0 1 0 0 0 1 1 0 0 0 inputs D N 0 0 0 1 1 0 0 0 1 1 - - next state D 3 D 2 D 1 0 0 0 1 0 - - 0 0 1 0 1 0 0 - - 0 1 0 0 - - 1 0 0 output D 0 open 1 0 0 0 0 0 1 D 0 = Q 0 D’ N’ D 1 = Q 0 N + Q 1 D’ N’ D 2 = Q 0 D + Q 1 N + Q 2 D’ N’ D 3 = Q 1 D + Q 2 N + Q 3 OPEN = Q 3 33

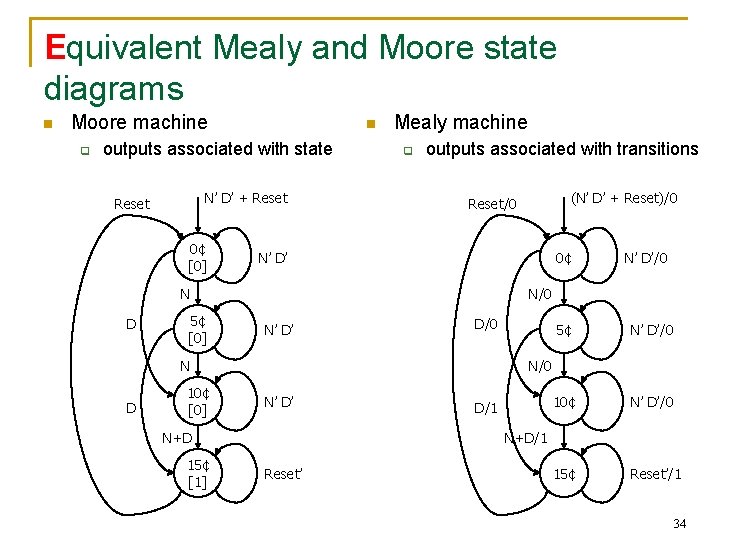
Equivalent Mealy and Moore state diagrams n Moore machine q n outputs associated with state N’ D’ + Reset 0¢ [0] Mealy machine q outputs associated with transitions 0¢ N’ D’ N D 5¢ [0] D N’ D’ D/0 5¢ N’ D’/0 10¢ N’ D’/0 15¢ Reset’/1 N/0 N’ D’ N+D 15¢ [1] N’ D’/0 N 10¢ [0] (N’ D’ + Reset)/0 Reset/0 D/1 N+D/1 Reset’ 34