Finite Element Method Course description n The course

Finite Element Method

Course description n The course aims to enable the students to understand the basic concepts and procedures of the finite element method (FEM) and to apply the FEM by using a commercial software ¨ Teaches understanding of how finite element methods work rather than how to use a software 2021/3/5 2

Softwares n MATLAB Ver. 6. 5 Strongly recommended software for matrix computation and programming n SAP 2000 Ver. 11. 0. 0 For applications 2021/3/5 3

Grading weights Homework assignments n Mid-semester exam n Take home test n Final exam-- project n 2021/3/5 15% 35% 4

Late coming to the class n n n The tolerance for coming late to the class is 20 minutes. Those who come late more than 20 minutes are NOT allowed to attend the class. Please refer to the “FEM Lecture Plan” for more academic norms 2021/3/5 5

Any question about the course before we begin with the Overview of the FEM? 2021/3/5 6

Discussion: the task of a structural engineer n Let take a look on a typical job vacancy announcement that you may read once you graduate from your study 2021/3/5 7

2021/3/5 8

Discussion (cont’d) n n Why do you think a design engineer is required to master a structural analysis and design software? An engineer needs to understand the behavior of a structure so that he/she can make judicious decisions in design, retrofitting, or rehabilitation of the structure 2021/3/5 9

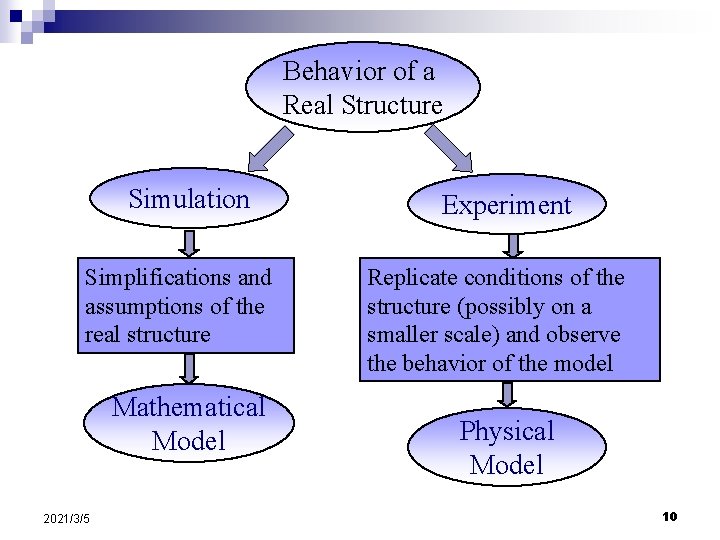
Behavior of a Real Structure Simulation Simplifications and assumptions of the real structure Mathematical Model 2021/3/5 Experiment Replicate conditions of the structure (possibly on a smaller scale) and observe the behavior of the model Physical Model 10

An example of the FEM applications Real experiment It is often expensive or dangerous FE simulation It replicates conditions of the real experiment Source: W. J. Barry (2003), “FEM Lecture Slides”, AIT Thailand 2021/3/5 11

The need for modeling n n n A real structure cannot be analyzed, it can only be “load tested” to determine the responses We can only analyze a “model” of the structure (perform simulation) We need to model the structure as close as possible to represent the behavior of the real structure Source: W. Kanok-Nukulchai 2021/3/5 12

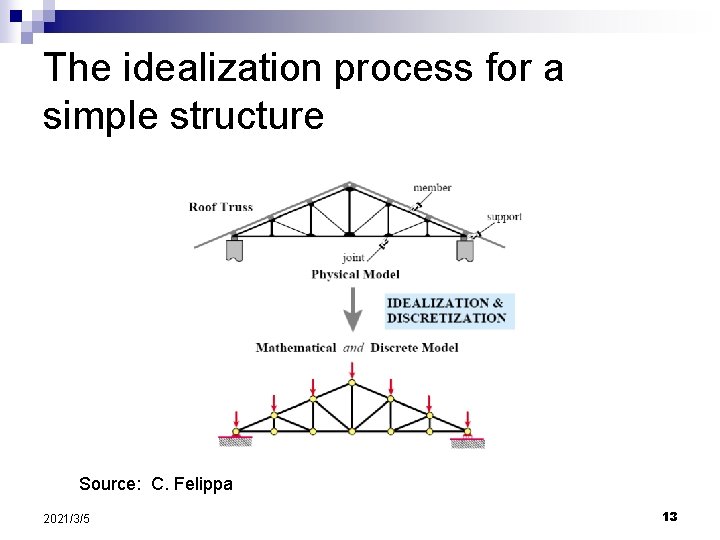
The idealization process for a simple structure Source: C. Felippa 2021/3/5 13

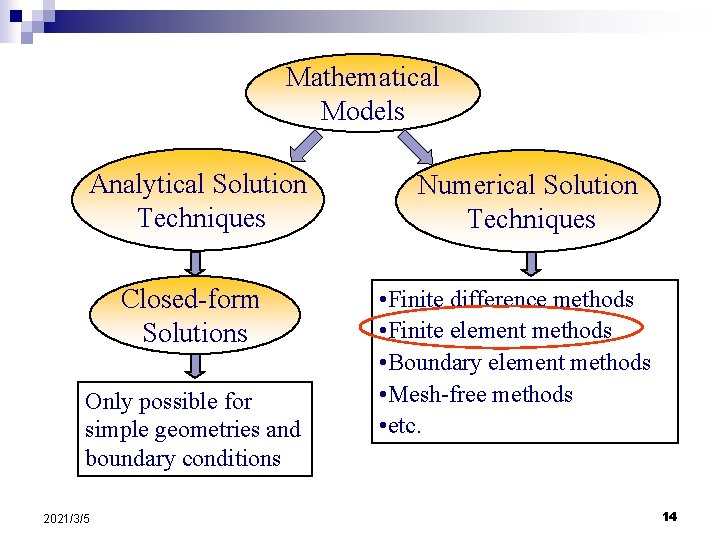
Mathematical Models Analytical Solution Techniques Closed-form Solutions Only possible for simple geometries and boundary conditions 2021/3/5 Numerical Solution Techniques • Finite difference methods • Finite element methods • Boundary element methods • Mesh-free methods • etc. 14

Finite element method (1) n n It is a computational technique used to obtain approximate solutions of engineering problems. In the context of structural analyzes, it may be regarded as a generalized direct stiffness method. ¨ n The direct stiffness method you studied in MK 4215 Structural Analysis III is actually the application of the FEM to frame structures It is originated as a method of structural analysis but is now widely used in various disciplines such as heat transfer, fluid flow, seepage, electricity and magnetism, and others. 2021/3/5 15

Finite element method (2) n Modern FEM were first developed and applied by aeronautical engineers, i. e. M. J. Turner et al. , at Boeing company in the period 1950 s. ¨ 2021/3/5 1956: The first engineering FEM paper 16

Finite element method (3) n n The name “finite element method” was coined by R. W. Clough in 1960. It is called “finite” in order to distinguish with “infinitesimal element” in Calculus. 1967: First FEM book by O. C. Zienkiewicz 2021/3/5 17

Finite element method (4) n n The computation is carried out automatically using a computer or a network of computers. The results are generally not exact. 2021/3/5 18

Example of applications in structural engineering 1. Framed structures (b) Grid (a) Truss Source: Weaver and Johnston, 1984 2021/3/5 19

Example of applications in structural engineering (cont’d) 1. Framed structures (cont’d) (c) Frame (d) Arch Source: Weaver and Johnston, 1984 2021/3/5 20

Example of applications in structural engineering (cont’d) 2. Two-dimensional continua (b) Plane strain (a) Plane stress Source: Weaver and Johnston, 1984 2021/3/5 21

Example of applications in structural engineering (cont’d) 3. Three-dimensional continua (a) General solid (b) Axisymmetric solid Source: Weaver and Johnston, 1984 2021/3/5 22

Example of applications in structural engineering (cont’d) 4. Plate in bending Source: Weaver and Johnston, 1984 2021/3/5 23

Example of applications in structural engineering (cont’d) 5. Shells (a) General shell (b) Axis symmetric shell Source: Weaver and Johnston, 1984 2021/3/5 24

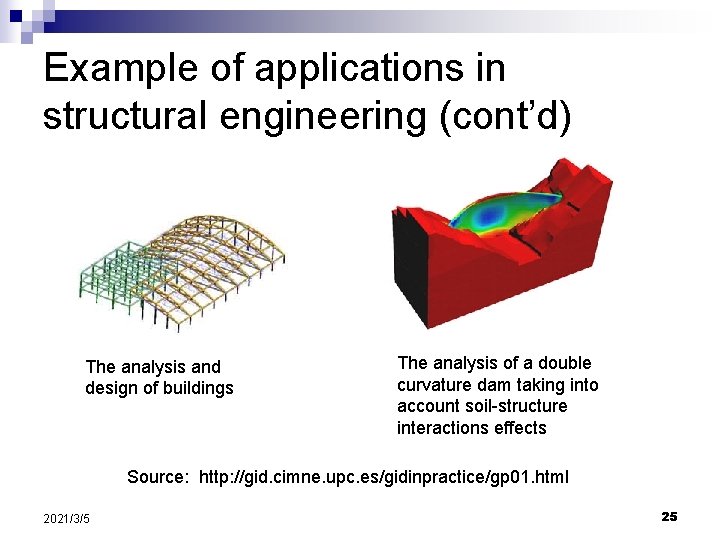
Example of applications in structural engineering (cont’d) The analysis and design of buildings The analysis of a double curvature dam taking into account soil-structure interactions effects Source: http: //gid. cimne. upc. es/gidinpractice/gp 01. html 2021/3/5 25

Example of applications in structural engineering (cont’d) The structural analysis of an F-16 aircraft The analysis of the Cathedral of Barcelona using 3 D solid elements. (courtesy of Barcelona Cathedral) Source: http: //gid. cimne. upc. es/gidinpractice/gp 01. html 2021/3/5 26

Discretization (1) n n Fundamental concept is discretization, i. e. dividing a continuum (continuous body, structural system) into a finite number of smaller and simple elements whose union approximates the geometry of the continuum. Mesh generation programs, called preprocessors, help the user in doing this work ¨ 2021/3/5 Gi. D, a software for pre and post processor 27

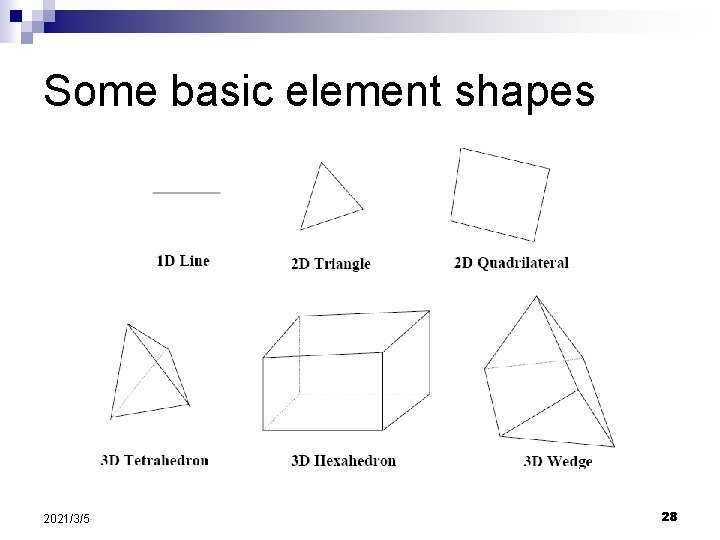
Some basic element shapes 2021/3/5 28

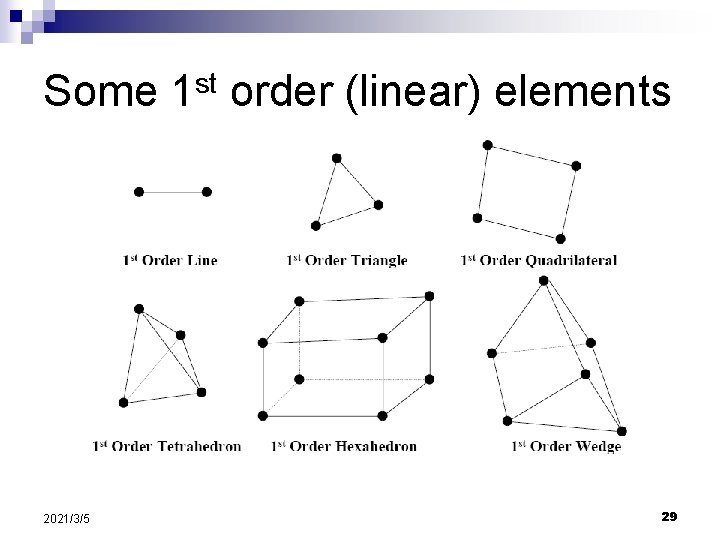
Some 1 st order (linear) elements 2021/3/5 29

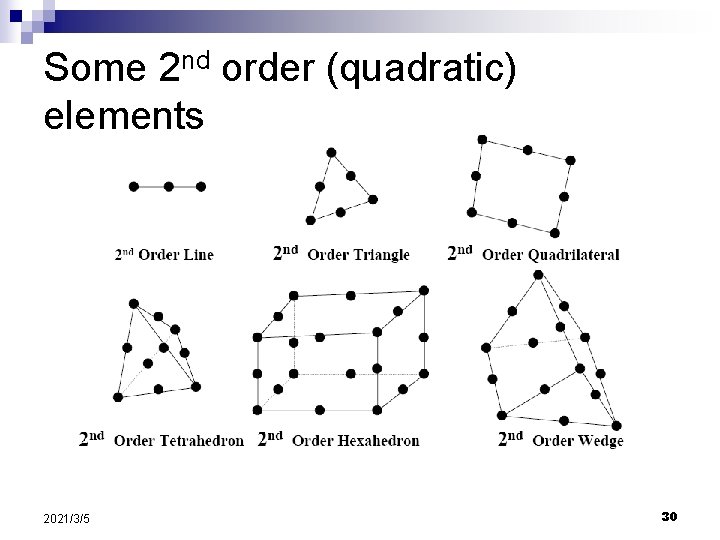
Some 2 nd order (quadratic) elements 2021/3/5 30

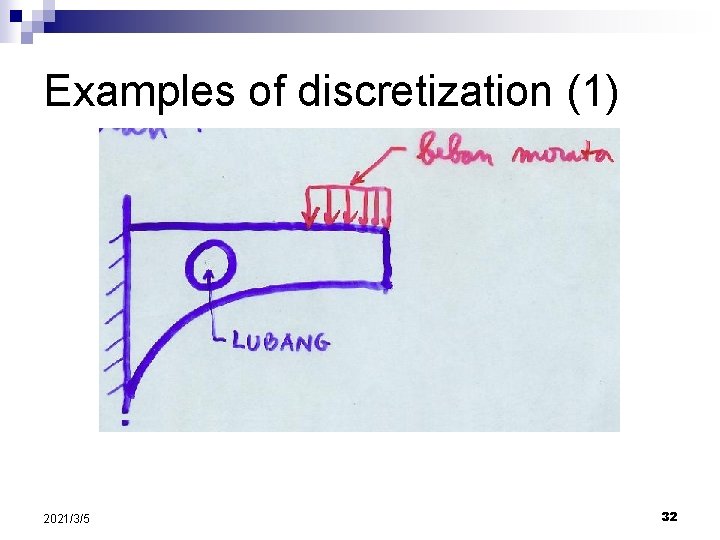
Discretization (2) n n One suggestion on performing discretization is to divide structural regions with high stress concentration into finer division e. g. in the vicinity of the support and around the hole(s). The accuracy of the results can be improved by using a finer mesh (h-refinement) or using a higher order elements (p-refinement). 2021/3/5 31

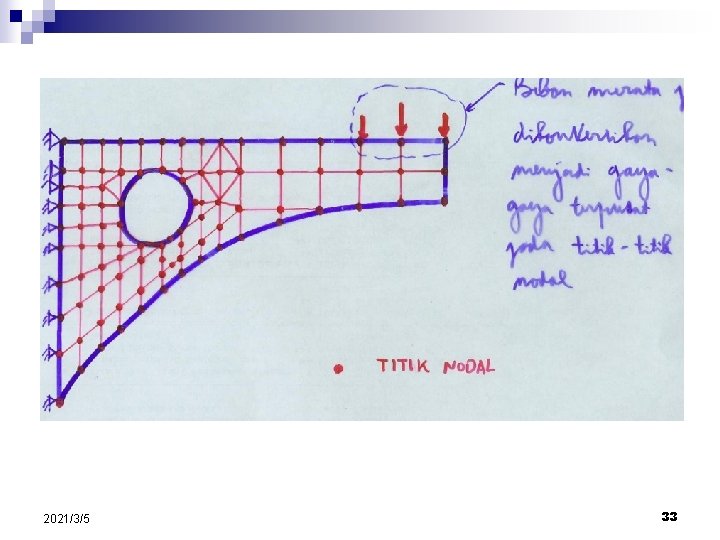
Examples of discretization (1) 2021/3/5 32

2021/3/5 33

Examples of discretization (2) z y x h D Clamped D=100, D/h =100 E = 2 x 106 ; ν = 0. 3; k = 5/6 Load: uniform q = -1 E-6 2021/3/5 76 nodes, 119 elements 172 active DOF 34

Examples of discretization (3) Cooling Tower– Nuclear Power Plant (taken from a FEM Course Project of Doddy and Andre, Dec 2008) 150 m 2021/3/5 35

Structural Model and Its Example of the Analysis Results The structure is divided into smaller parts called “element” 2021/3/5 Membrane force contour in the circumferential direction 36

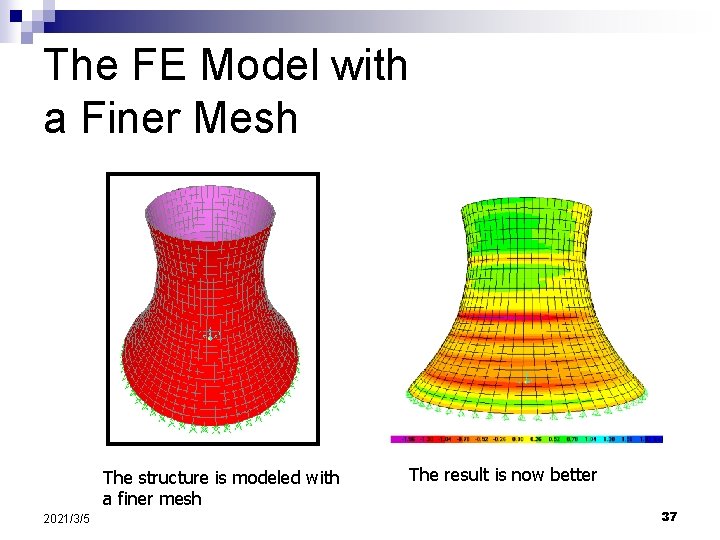
The FE Model with a Finer Mesh The structure is modeled with a finer mesh 2021/3/5 The result is now better 37

Examples of FEM software n n n For General purposes: NASTRAN, ANSYS, ADINA, ABAQUS, etc. For structural analysis, particularly in Civil Engineering: SANS, SAP, STAAD, GT STRUDL, etc. For building structures: ETABS, BATS etc. For geotechnical design: PLAXIS For conducting researches on earthquake engineering: DRAIN-2 D, DRAIN-3 D, RUAOMOKO, Open. Sees etc. 2021/3/5 38

Typical capabilities of a FE program n Data generation ¨ n Element types ¨ n Linear-elastic, nonlinear Load types ¨ n E. g. SAP 2000: Frame, Cable, Shell, Plane, Asolid, Solid, etc. Material behavior ¨ n Automatic generation of nodes, elements, and restraints Force, displacement, thermal, time-varying excitation Plotting results ¨ 2021/3/5 Original and deformed geometry, stress contours 39

Why do we need to study the basic theory of FEM? n n Cook, Malkus, and Plesha (1989, pp. 6) Concepts and assumptions behind the computer codes (FEM software) should be mastered. Engineers are expected to be able to use the software to gain better advantages and will less likely misuse them. SAP 2000 disclaimer The user accepts and understands that no warranty is expressed or implied by the developers or the distributors on the accuracy or reliability of the program. The user must explicitly understand the assumptions of the program and must independently verify the results. 2021/3/5 40

Any question before we proceed to computational steps of the FEM? 2021/3/5 41

Computational steps of the FEMthe direct stiffness method n Discretize the structure (problem domain) ¨ n n Divide the structure or continuum into finite elements Once the structure has been discretized, the computational steps faithfully follow the steps in the direct stiffness method. The direct stiffness method: ¨ 2021/3/5 The global stiffness matrix of the discrete structure are obtained by superimposing (assembling) the stiffness matrices of the element in a direct manner. 42

Computational steps… (cont’d) n n Generate element stiffness matrix and element force matrix for each element. Assemble the element matrices to obtain the global stiffness equation of the structure. Apply the known nodal loads. Specify how the structure is supported: ¨ Set 2021/3/5 several nodal displacements to known values. 43

General steps of the FEM (cont’d) Solve simultaneous linear algebraic equation. The nodal parameters (displacements) are obtained. n Calculate element stresses or stress resultants (internal forces). n 2021/3/5 44

Any question before we continue to a brief introduction to MATLAB? 2021/3/5 45

Example n n Suppose you want to calculate the natural frequency (Hz) of a SDOF system with the mass m=100 kg and stiffness k=5 KN/m The formula is Type in the Command Window: >>m=100 >>k=5*1000 >> f=1/(2*pi)*sqrt(k/m) n 2021/3/5 46

Edit/Debug Window Click this icon to open a new Edit/Debug window 2021/3/5 47

Array and matrix operations Array operations are operations performed between arrays on an element-by-element basis, e. g. >> A=[ 1 2; 3 4], B=[-1 3; -2 1] >> A+B, A+4 n Common array operations: n ¨ Array multiplication (A. * B) ¨ Array right division (A. / B) ¨ Array left division (A. B) B in the numerator ¨ Array exponential (A. ^ B) 2021/3/5 48

Matrix operations follow the normal rules of linear algebra, e. g. >> A=[ 1 2; 3 4] >> B=[-1 3; -2 1] >> A*B n What is the different between A. ^3 and A^3? n Be careful to distinguish between array operations and matrix operations in your MATLAB code 2021/3/5 49

Solving a set of linear algebraic equations The equations can be written in matrix form as follows: 2021/3/5 50

Solving a set of linear algebraic equations (cont’d) MATLAB command to solve the equations: >> x= A B (left division operator) n Other commands related to linear algebra: >> det (A) >> rank (A) >> inv (A) n 2021/3/5 51

Please look at the Matlab Tutorial folder to learn more about Matlab 2021/3/5 52

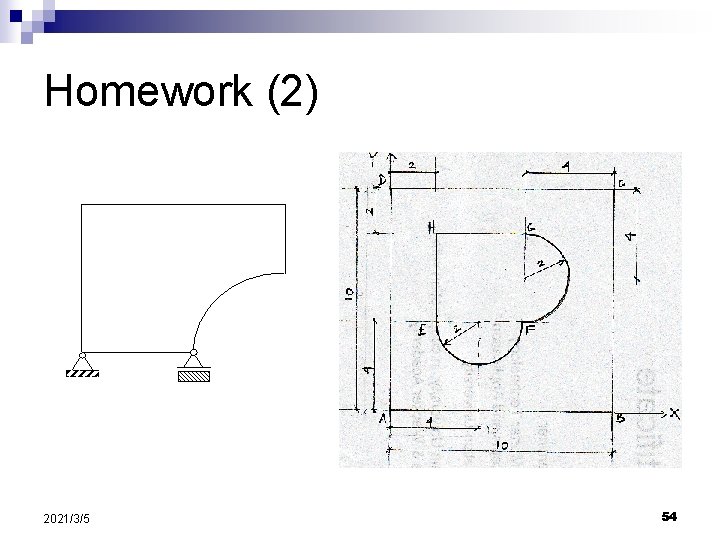
Homework (due date next class) Write an essay explaining (approx. 500 words): 1. What is finite element method? ¨ Why do you interested to take this course (TS 4466 Finite Element Method)? What do you expect? ¨ 2. 2021/3/5 Divide the following continuum into finite elements: 53

Homework (2) 2021/3/5 54

Homework (3) 3. Divide this equilateral triangle into several quadrilateral elements. You are not allowed to use a triangular element. 4. Solve the following simultaneous algebraic equations using Matlab. 2021/3/5 55

a. b. Explain why the second equation (No. b) does not have a unique solution? (Connect this fact with the determinant and the rank of the coefficient matrix) 2021/3/5 56