Finite Element Method CHAPTER 3 THE FINITE ELEMENT

Finite Element Method CHAPTER 3: THE FINITE ELEMENT METHOD 1

CONTENTS STRONG AND WEAK FORMS OF GOVERNING EQUATIONS l HAMILTON’S PRINCIPLE l FEM PROCEDURE l – – – – Domain discretization Displacement interpolation Formation of FE equation in local coordinate system Coordinate transformation Assembly of FE equations Imposition of displacement constraints Solving the FE equations STATIC ANALYSIS l EIGENVALUE ANALYSIS l TRANSIENT ANALYSIS l REMARKS l Finite Element Method by G. R. Liu and S. S. Quek 2

STRONG AND WEAK FORMS OF GOVERNING EQUATIONS l l l System equations: strong form, difficult to solve. Weak form: requires weaker continuity on the dependent variables (u, v, w in this case). Weak form is often preferred for obtaining an approximated solution. Formulation based on a weak form leads to a set of algebraic system equations – FEM can be applied for practical problems with complex geometry and boundary conditions. Finite Element Method by G. R. Liu and S. S. Quek 3

HAMILTON’S PRINCIPLE l “Of all the admissible time histories of displacement the most accurate solution makes the Lagrangian functional a minimum. ” l An admissible displacement must satisfy: – The compatibility equations – The essential or the kinematic boundary conditions – The conditions at initial (t 1) and final time (t 2) Finite Element Method by G. R. Liu and S. S. Quek 4

HAMILTON’S PRINCIPLE l Mathematically where L=T-P+Wf (Kinetic energy) (Potential energy) (Work done by external forces) Finite Element Method by G. R. Liu and S. S. Quek 5

FEM PROCEDURE l l l l Step 1: Domain discretization Step 2: Displacement interpolation Step 3: Formation of FE equation in local coordinate system Step 4: Coordinate transformation Step 5: Assembly of FE equations Step 6: Imposition of displacement constraints Step 7: Solving the FE equations Finite Element Method by G. R. Liu and S. S. Quek 6

Step 1: Domain discretization l l l The solid body is divided into Ne elements with proper connectivity – compatibility. All the elements form the entire domain of the problem without any overlapping – compatibility. There can be different types of element with different number of nodes. The density of the mesh depends upon the accuracy requirement of the analysis. The mesh is usually not uniform, and a finer mesh is often used in the area where the displacement gradient is larger. Finite Element Method by G. R. Liu and S. S. Quek 7

Step 2: Displacement interpolation l Bases on local coordinate system, the displacement within element is interpolated using nodal displacements. Finite Element Method by G. R. Liu and S. S. Quek 8

Step 2: Displacement interpolation l. N is a matrix of shape functions Shape function for each displacement component at a node where Finite Element Method by G. R. Liu and S. S. Quek 9

Displacement interpolation l Constructing shape functions – Consider constructing shape function for a single displacement component – Approximate in the form p. T(x)={1, x, x 2, x 3, x 4, . . . , xp} (1 D) Finite Element Method by G. R. Liu and S. S. Quek 10

Pascal triangle of monomials: 2 D Finite Element Method by G. R. Liu and S. S. Quek 11

Pascal pyramid of monomials : 3 D Finite Element Method by G. R. Liu and S. S. Quek 12

Displacement interpolation – Enforce approximation to be equal to the nodal displacements at the nodes di = p. T(xi) i = 1, 2, 3, …, nd or de=P where , Finite Element Method by G. R. Liu and S. S. Quek 13

Displacement interpolation – The coefficients in can be found by – Therefore, uh(x) = N( x) de Finite Element Method by G. R. Liu and S. S. Quek 14

Displacement interpolation l Sufficient requirements for FEM shape functions (Delta function property) 1. 2. (Partition of unity property – rigid body movement) 3. (Linear field reproduction property) Finite Element Method by G. R. Liu and S. S. Quek 15

Step 3: Formation of FE equations in local coordinates Strain matrix Since U= Nde Therefore, e = LU Π= e = L N de = B de 1 1 1 T T T = = ε c ε d V d B c Bd d V d ( B c. Bd. V )d e ò ò e e e ò 2 Ve or where T = k e ò B c. Bd. V Ve (Stiffness matrix) Finite Element Method by G. R. Liu and S. S. Quek 16

Step 3: Formation of FE equations in local coordinates Since U= Nde or where (Mass matrix) Finite Element Method by G. R. Liu and S. S. Quek 17

Step 3: Formation of FE equations in local coordinates (Force vector) Finite Element Method by G. R. Liu and S. S. Quek 18

Step 3: Formation of FE equations in local coordinates (Hamilton’s principle) FE Equation Finite Element Method by G. R. Liu and S. S. Quek 19

Step 4: Coordinate transformation (Local) y' Global coordinate systems (Global) x' Local coordinate systems y' y where x' x , , Finite Element Method by G. R. Liu and S. S. Quek 20

Step 5: Assembly of FE equations l Direct assembly method – Adding up contributions made by elements sharing the node (Static) Finite Element Method by G. R. Liu and S. S. Quek 21

Step 6: Impose displacement constraints rigid body movement (meaningless for static analysis) l Remove rows and columns corresponding to the degrees of freedom being constrained l K is semi-positive definite l No Finite Element Method by G. R. Liu and S. S. Quek 22

Step 7: Solve the FE equations l Solve the FE equation, for the displacement at the nodes, D l The strain and stress can be retrieved by using e = LU and s = c e with the interpolation, U=Nd Finite Element Method by G. R. Liu and S. S. Quek 23

STATIC ANALYSIS l Solve KD=F for D – Gauss elmination – LU decomposition – Etc. Finite Element Method by G. R. Liu and S. S. Quek 24

EIGENVALUE ANALYSIS (Homogeneous equation, F = 0) Assume Let (Roots of equation are the eigenvalues) [ K - li M ] fi = 0 (Eigenvector) Finite Element Method by G. R. Liu and S. S. Quek 25

EIGENVALUE ANALYSIS l Methods of solving eigenvalue equation – Jacobi’s method – Given’s method and Householder’s method – The bisection method (Sturm sequences) – Inverse iteration – QR method – Subspace iteration – Lanczos’ method Finite Element Method by G. R. Liu and S. S. Quek 26

TRANSIENT ANALYSIS Structure systems are very often subjected to transient excitation. l A transient excitation is a highly dynamic time dependent force exerted on the structure, such as earthquake, impact, and shocks. l The discrete governing equation system usually requires a different solver from that of eigenvalue analysis. l The widely used method is the so-called direct integration method. l Finite Element Method by G. R. Liu and S. S. Quek 27

TRANSIENT ANALYSIS The direct integration method is basically using the finite difference method for time stepping. l There are mainly two types of direct integration method; one is implicit and the other is explicit. l Implicit method (e. g. Newmark’s method) is more efficient for relatively slow phenomena l Explicit method (e. g. central differencing method) is more efficient for very fast phenomena, such as impact and explosion. l Finite Element Method by G. R. Liu and S. S. Quek 28

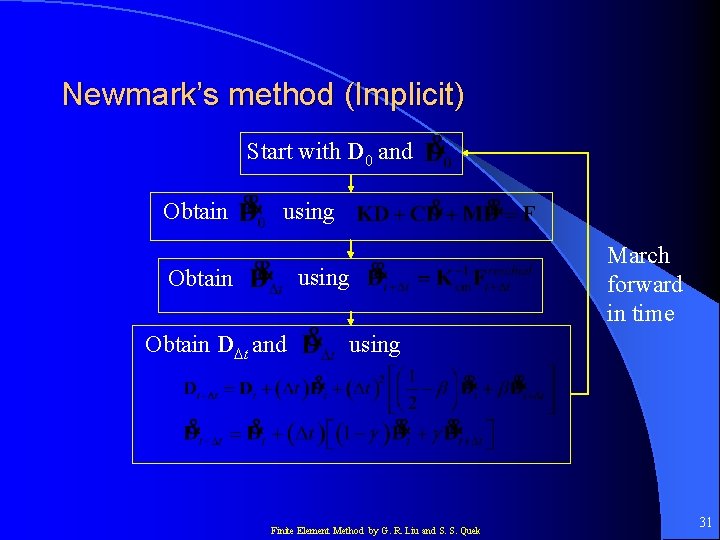
Newmark’s method (Implicit) Assume that Substitute into Finite Element Method by G. R. Liu and S. S. Quek 29

Newmark’s method (Implicit) where Therefore, Finite Element Method by G. R. Liu and S. S. Quek 30

Newmark’s method (Implicit) Start with D 0 and Obtain using Obtain D t and March forward in time using Finite Element Method by G. R. Liu and S. S. Quek 31

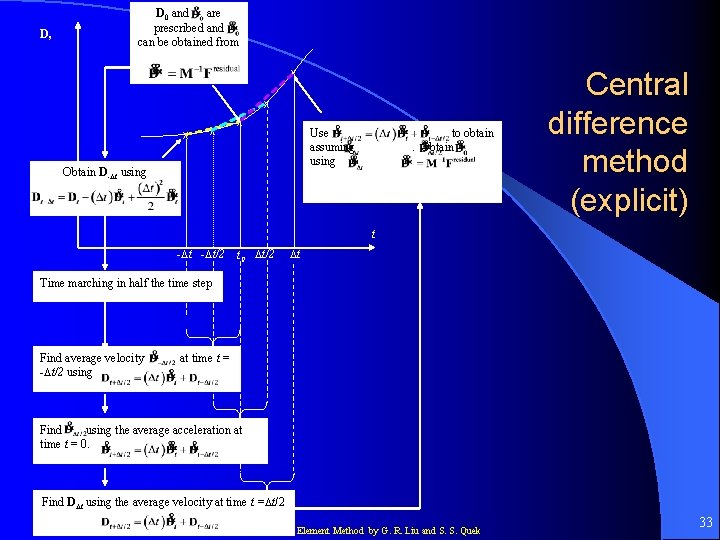
Central difference method (explicit) (Lumped mass – no need to solve matrix equation) Finite Element Method by G. R. Liu and S. S. Quek 32

D, D 0 and are prescribed and can be obtained from x x x Use assuming using Obtain D- t using to obtain. Obtain Central difference method (explicit) t - t/2 t 0 t/2 t Time marching in half the time step Find average velocity - t/2 using at time t = Find using the average acceleration at time t = 0. Find D t using the average velocity at time t = t/2 Finite Element Method by G. R. Liu and S. S. Quek 33

REMARKS In FEM, the displacement field U is expressed by displacements at nodes using shape functions N defined over elements. l The strain matrix B is the key in developing the stiffness matrix. l To develop FE equations for different types of structure components, all that is needed to do is define the shape function and then establish the strain matrix B. l The rest of the procedure is very much the same for all types of elements. l Finite Element Method by G. R. Liu and S. S. Quek 34