FINITE ELEMENT APPROXIMATION RayleighRitz method approximate solution in

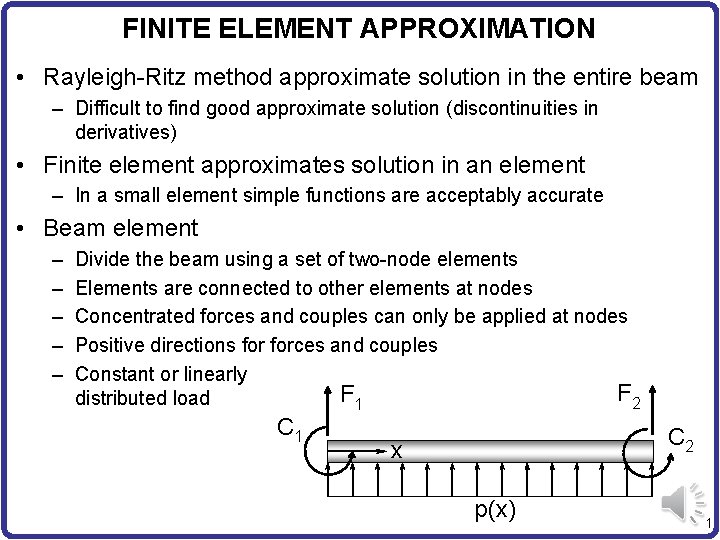
FINITE ELEMENT APPROXIMATION • Rayleigh-Ritz method approximate solution in the entire beam – Difficult to find good approximate solution (discontinuities in derivatives) • Finite element approximates solution in an element – In a small element simple functions are acceptably accurate • Beam element – – – Divide the beam using a set of two-node elements Elements are connected to other elements at nodes Concentrated forces and couples can only be applied at nodes Positive directions forces and couples Constant or linearly F 2 F 1 distributed load C 1 C 2 x p(x) 1

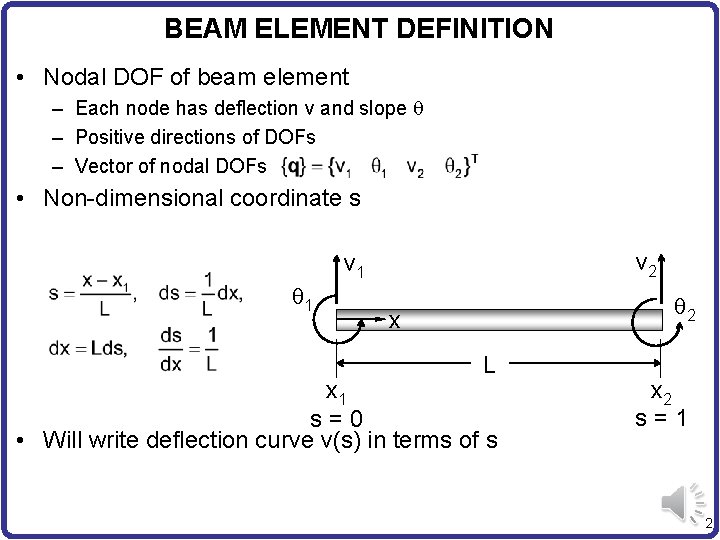
BEAM ELEMENT DEFINITION • Nodal DOF of beam element – Each node has deflection v and slope q – Positive directions of DOFs – Vector of nodal DOFs • Non-dimensional coordinate s q 1 v 2 v 1 q 2 x L x 1 s=0 • Will write deflection curve v(s) in terms of s x 2 s=1 2

BEAM ELEMENT INTERPOLATION • Deflection interpolation – Interpolate the deflection v(s) in terms of four nodal DOFs – Use cubic polynomial: – Relation to the slope: – Apply four conditions: – Express four coefficients in terms of nodal DOFs 3

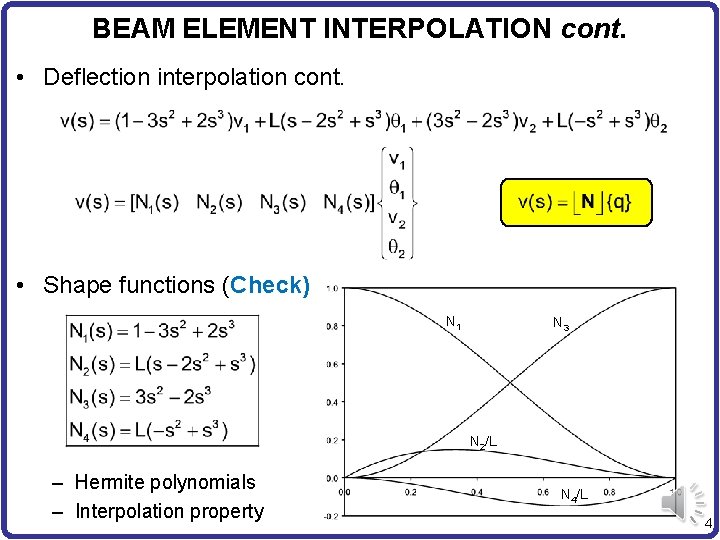
BEAM ELEMENT INTERPOLATION cont. • Deflection interpolation cont. • Shape functions (Check) N 1 N 3 N 2/L – Hermite polynomials – Interpolation property N 4/L 4

Quiz-like problems • What are the common properties of all four Hermite interpolation functions? • What is the slope of N 1 at x=L? • What is the value of N 2 at x=L? • What is the slope of N 2 at x=L? • A race car sensors show that at t=0 it had zero speed an acceleration of 2 g, and at t=2 sec it had a speed of 30 m/s and an acceleration of 1 g. Use Hermite interpolation to estimate its speed at t=1 sec (replace x by t, L=2 sec, v is speed, and replace q by the acceleration a) • Answers in notes page. 5

BEAM ELEMENT INTERPOLATION cont. • Properties of interpolation – Deflection is a cubic polynomial (discuss accuracy and limitation) – Interpolation is valid within an element, not outside of the element – Adjacent elements have continuous deflection and slope • Approximation of curvature – Curvature is second derivative and related to strain and stress B: strain-displacement vector – B is linear function of s and, thus, the strain and stress – Alternative expression: – If the given problem is linearly varying curvature, the approximation is exact; if higher-order variation of curvature, then it is approximate 6

BENDING MOMENT AND SHEAR • Approximation of bending moment and shear force Linear Constant – Stress is proportional to M(s); M(s) is linear; stress is linear, too – Maximum stress always occurs at the node – Bending moment and shear force are not continuous between adjacent elements 7

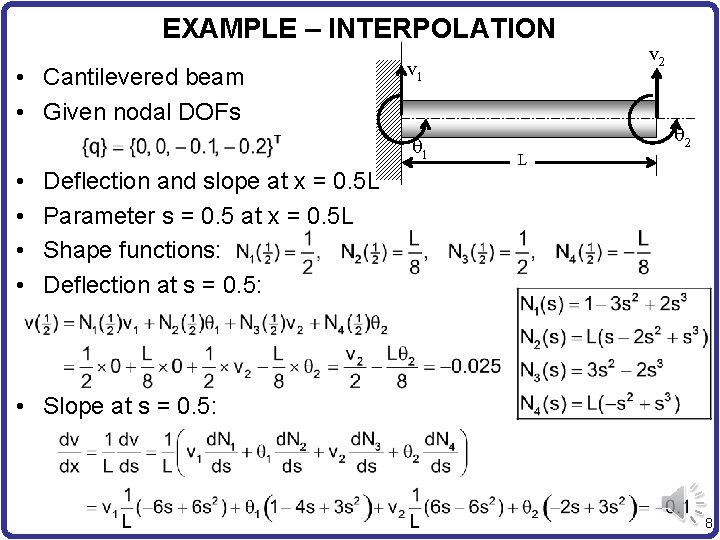
EXAMPLE – INTERPOLATION • Cantilevered beam • Given nodal DOFs v 1 q 1 • • Deflection and slope at x = 0. 5 L Parameter s = 0. 5 at x = 0. 5 L Shape functions: Deflection at s = 0. 5: v 2 q 2 L • Slope at s = 0. 5: 8

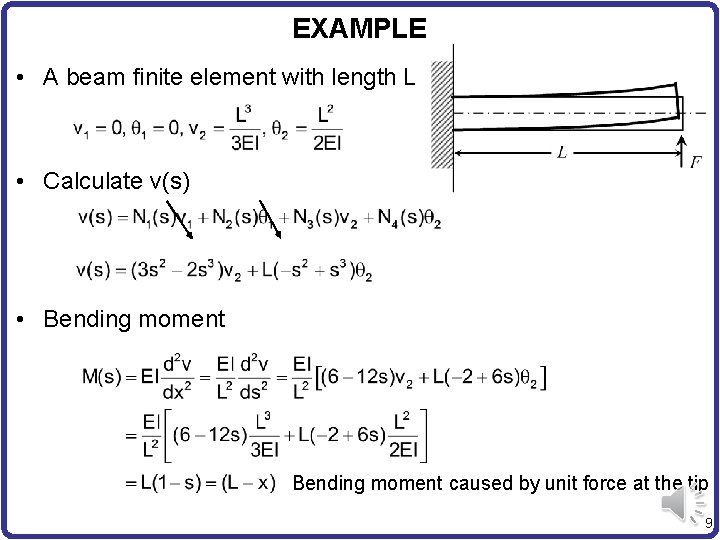
EXAMPLE • A beam finite element with length L • Calculate v(s) • Bending moment caused by unit force at the tip 9

Quiz-like problem • What is the tip force and couple that we will need to apply to a cantilever beam of length L and stiffness EI so that it will have a unit displacement and zero slope? • Answer in the notes page 10