Finite Differences By Daniela G Ambrosano Finite Differences

Finite Differences By Daniela G. Ambrosano

Finite Differences v Finite differences is a method to find the polynomial that could generate a sequence, assuming the sequence can be generated by a polynomial.

Finding Successive Differences Find successive difference between terms of sequence; the difference sequence. Term #n f(n) 1 5 2 15 - 5 = 10 3 33 - 15 = 18 4 59 – 33 =26 5 93 – 59 = 34 v

Finding differences, continued… Continue finding differences between the terms of difference sequences until the difference sequence is a constant. Term#n f(n) 1 5 2 15 - 5 = 10 3 33 - 15 = 18 - 10 = 8 4 59 - 33 = 26 - 18 = 8 5 93 - 59 = 34 - 26 = 8 v

Continuing on… v The second difference in the sequence is constant so we need a 2 nd degree polynomial. v General Form:

Why? v The number of difference sequences is the power of the polynomial that generated the original sequence. v This is because it takes that many derivatives to get to a constant.

Generating a system (n+1) equations in (n+1) variables v The variables in (n+1) are the coefficients of the general polynomial. v To generate a system (n+1) equations in (n+1) variables, we subtract the various term numbers to equal the corresponding term values. For n = 1

Polynomials v For n=1 v For n = 2 v For n = 3

Solve the System of Equations v Solve the system of equations to find the coefficients/variables in two ways: *substitution *elimination

Eliminating C v Take the 2 nd equation for n=2 and subtract from it the 1 st equation for n=1 v Now take the 3 rd equation for n=3 and subtract from it the 2 nd equation for n=2

Eliminate b and Solve for a v Now we use the new equations 3 a + b = 10 and 5 a + b = 18, subtract them and then solve for a

Substituting v Now we can substitute a = 4 in 3 a + b = 10 to find the value of b v Then substitute the values of a = 4 and b = -2 into the 1 st equation a + b + c = 5 to find the value of c

What is f(n)? v Now that we know the values of a, b, and c we can substitute them into the original 2 nd degree polynomial that will generate the difference sequences.

Check Polynomial v Plug in a value for n to check if the polynomial generated is correct Ex: n = 2

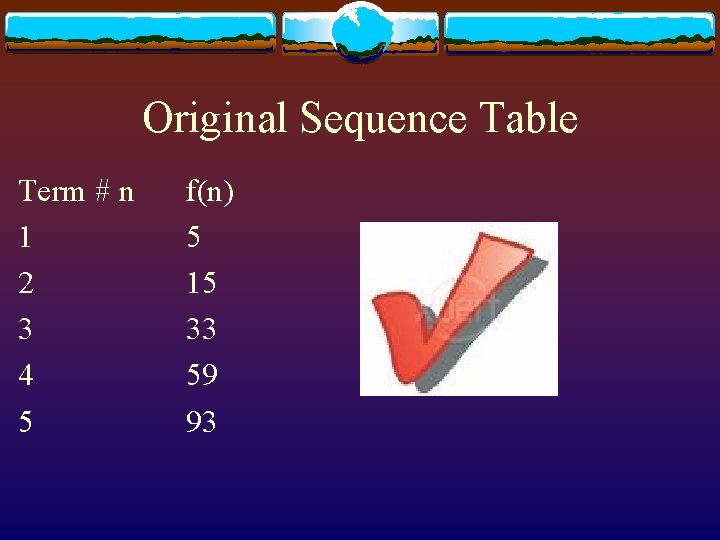
Original Sequence Table Term # n 1 2 3 4 5 f(n) 5 15 33 59 93

The End