Finite Difference Methods 3 8 Practical Applications Wave

Finite Difference Methods 3. 8 Practical Applications Ⅱ - Wave Scattering 3. 9 Absorbing Boundary Conditions for FDTD 3. 10 Finite Difference for Nonrectangular Systems 3. 11 Numerical Integration

3. 8 Practical Applications Ⅱ - Wave Scattering(FDTD) � FDTD(Finite-Difference Time-Domain)는 Yee에 의해 처음 소개되었고, 후에 Taflove 등 많은 사람들에 의해 발전되었다. FDTD방법은 time-dependent한 Maxwell의 curl equation의 직접적 solution이다. � 이 장에서 살펴볼 FD-TD에 대한 내용 • Yee‘s finite difference algorithm • accuracy and stability • absorbing boundary conditions • initial fields • programming aspects 1

� 0<y<Jmax δ 일 때 truncation condition (12 e) (12 f) (12 g) (12 h) � 0<z<Kmax δ일 때 truncation condition (12 i) (12 j) (12 k) (12 l) 10

� 0<y<Jmax δ 일 때 truncation condition 11

3. 8. 4 Initial Fields � initial field component는 incident plane wave pulse 나 single-frequency plane wave 를 simulating 해서 구할 수 있다. simulation은 excessive storage 를 취하거나 불요 전파 반사(spurious wave-reflection)를 일으켜선 안된다. � 3차원의 경우 y=js(near y=0)에서의 wave source condition은 (13) 3. 8. 5 Programming Aspects � 대부분의 EM scattering문제들이 nonmagnetic media(μr=1)에서 일어나기 때문 에 δt/μ(i, j, k)δ는 상수라고 가정할 수 있다. (이로써 앞의 식 (7)의 계산 시 9번의 곱 셈이 필요했는데 6번으로 줄어든다: 계산시간 감소) � Taflove 가 제안한대로 아래와 같은 상수를 정의한다. (14 a) (14 b) (14 c) (14 d) (14 e) m=MEDIA(i, j, k) : (i, j, k)지점에서 유전율/도전율 12

(21 c) (21 d) 20

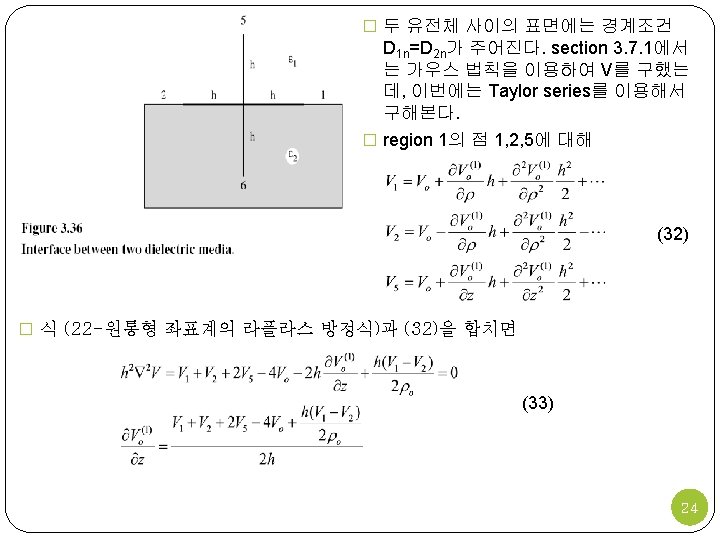
3. 10 Finite Differencing for Nonrectangular Systems 3. 10. 1 Finite Differencing for Nonrectangular Systems � 원통형 좌표계의 라플라스 방정식 (22) (24) � 그림의 점 O(ρo, φo, ｚo)에서 equivalent finite difference approximation은 (23) 21

3. 10. 2 Spherical Coordinates � 구형 좌표계의 라플라스 방정식 (37) � 점 O(ro, θo, φo)에서 equivalent finite difference approximation은 (38) 26

3. 11 Numerical Integration � numerical integration(numerical quadrature)은 이학/공학 등에서 쉽게 적분을 할 수 없거나 함수가 discrete data로 표현되는 경우에 사용된다. � numerical integration의 종류 • Euler‘s rule • Trapezoidal rule (사다리꼴 공식) • Simpson‘s rule • Newton-Cotes rules • Gaussian (quadrature) rules basic techniques advanced techniques 27

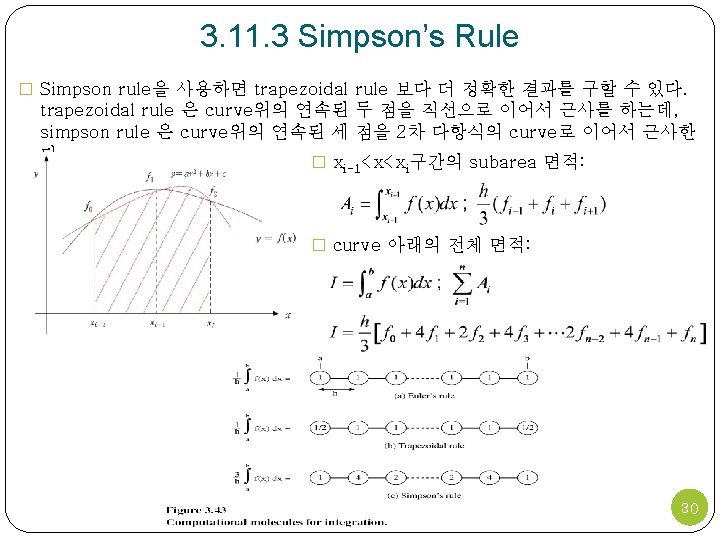
3. 11. 2 Trapezoidal Rule � 식 (3. 129)를 trapezoidal rule을 사용하여 계산한다. � xi-1<x<xi구간의 subarea 면적: � curve 아래의 전체 면적: 29

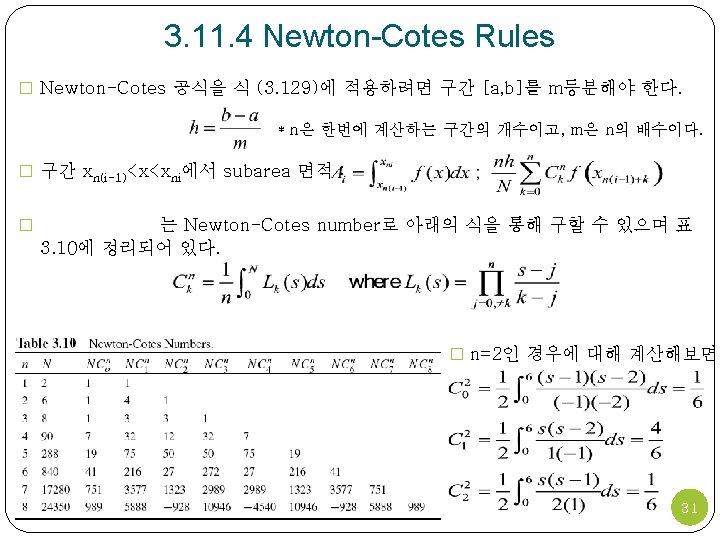
3. 11. 5 Gaussian Rules � Gaussian Rule � unequally spaced points 를 사용하여 수치적분 값을 구한다. � 유한한 구간에 대해 적분할 때는 Gauss-Legendre rule과 Gauss-Chebyshev rule을 사용. � Gauss-Legendre rule � Gauss-Chebyshev rule : Gauss-Legendre rule과 같은 식을 사용하나, sample point가 다르다. 33

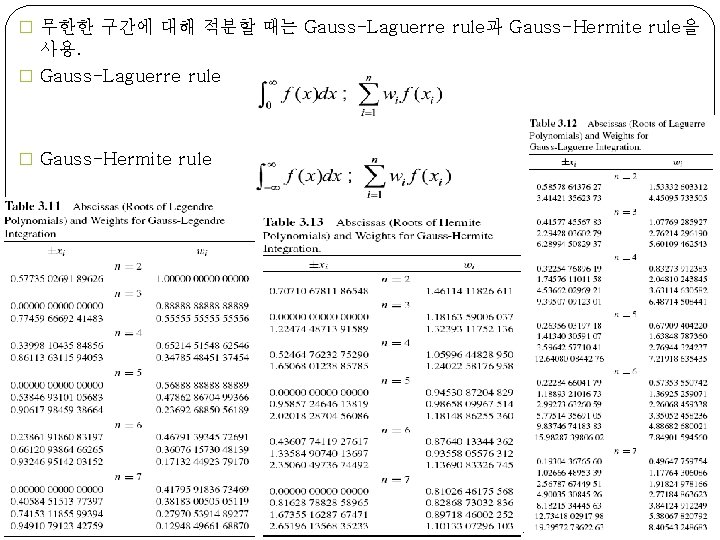
� 무한한 구간에 대해 적분할 때는 Gauss-Laguerre rule과 Gauss-Hermite rule을 사용. � Gauss-Laguerre rule � Gauss-Hermite rule 34