Finite Difference Discretization of Hyperbolic Equations Linear Problems

Finite Difference Discretization of Hyperbolic Equations: Linear Problems Lectures 8, 9 and 10

First Order Wave Equation INITION BOUNDARY VALUE PROBLEM (IBVP) Initial Condition: Boundary Conditions:

First Order Wave Equation Solution Characteristics General solution

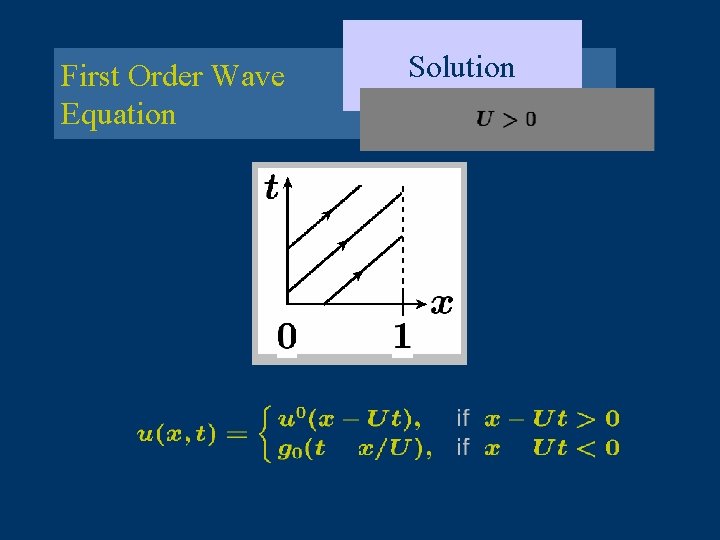
First Order Wave Equation Solution

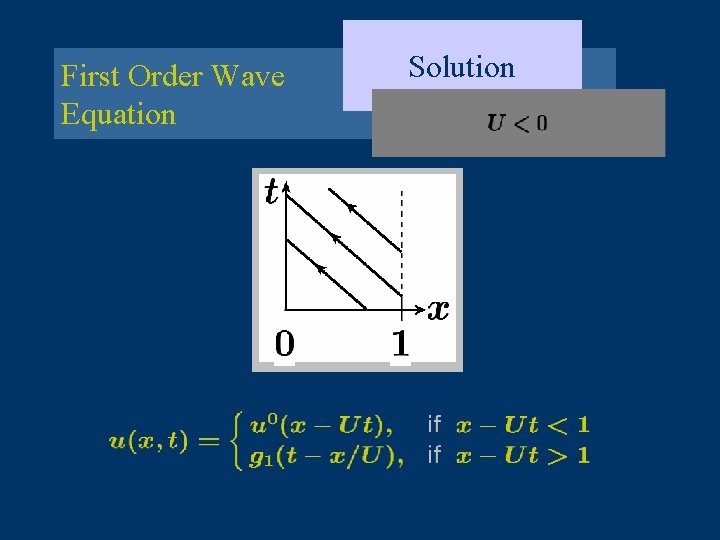
First Order Wave Equation Solution

First Order Wave Equation Stability

Model Problem Initial condition: Periodic Boundary conditions: constant

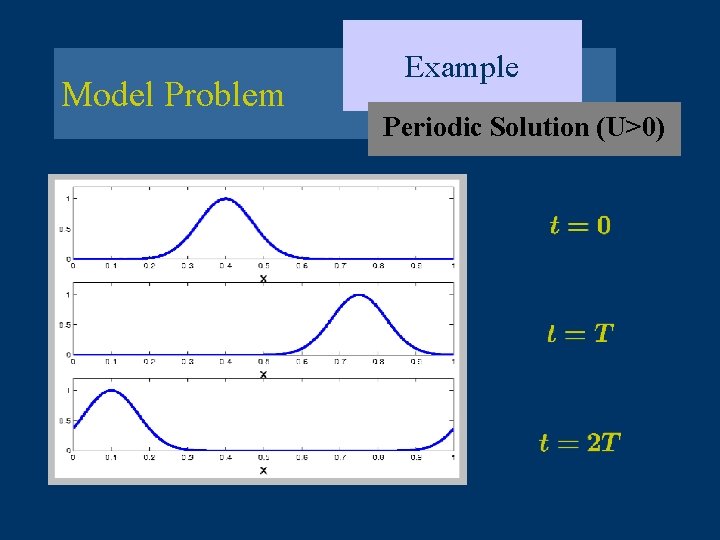
Model Problem Example Periodic Solution (U>0)

Finite Difference Solution Discretization Discretize (0, 1) into J equal intervals And (0, T) into N equal intervals

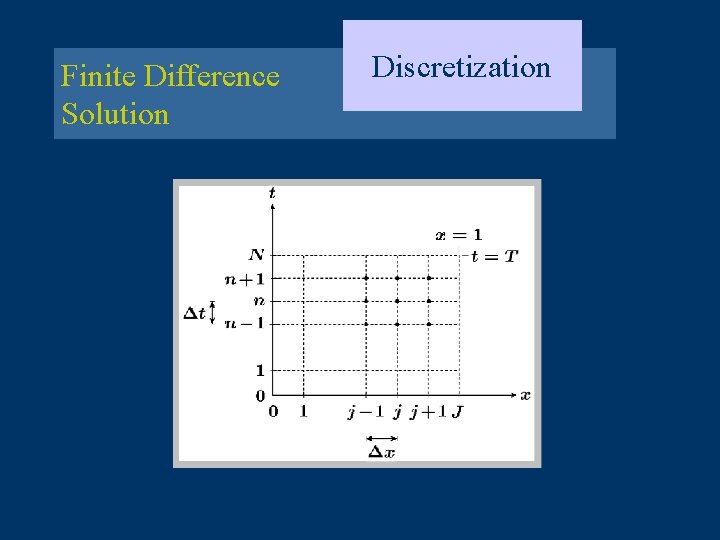
Finite Difference Solution Discretization

Finite Difference Solution Discretization NOTATION: • • • approximation to vector of approximate values at time vector of exact values at time ; ;

Finite Difference Solution Approximation For example … for ( U > 0 ) Forward in Time Backward (Upwind) in Space

Finite Difference Solution First Order Upwind Scheme suggests … Courant number C =

Finite Difference Solution First Order Upwind Scheme Interpretation Use Linear Interpolation j – 1, j

Finite Difference Solution First Order Upwind Scheme Explicit Solution no matrix inversion exists and is unique

Finite Difference Solution We can write First Order Upwind Scheme Matrix Form

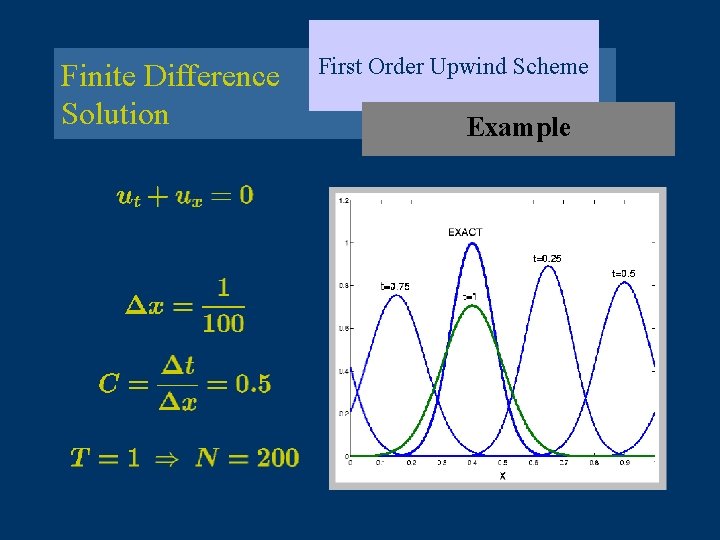
Finite Difference Solution First Order Upwind Scheme Example

Convergence Definition The finite difference algorithm converges if For any initial condition .

Definition Consistency The difference scheme , is consistent with the differential equation if: For all smooth functions when .

Consistency Difference operator Differential operator First Order Upwind Scheme

Consistency First Order Upwind Scheme First order accurate in space and time

Truncation Error Insert exact solution Consistency into difference scheme

Definition Stability The difference scheme There exists for all is stable if: such that ; and n, such that Above condition can be written as

Stability First Order Upwind Scheme

Stability First Order Upwind Scheme

Stability Stable if Upwind scheme is stable provided

Lax Equivalence Theorem A consistent finite difference scheme for a partial differential equation for which the initial value problem is well-posed is convergent if and only if it is stable.

Lax Equivalence Theorem Proof ( first order in ) ,

Lax Equivalence Theorem • Consistency: • Stability: • Convergence First Order Upwind Scheme for or and are constants independent of ,

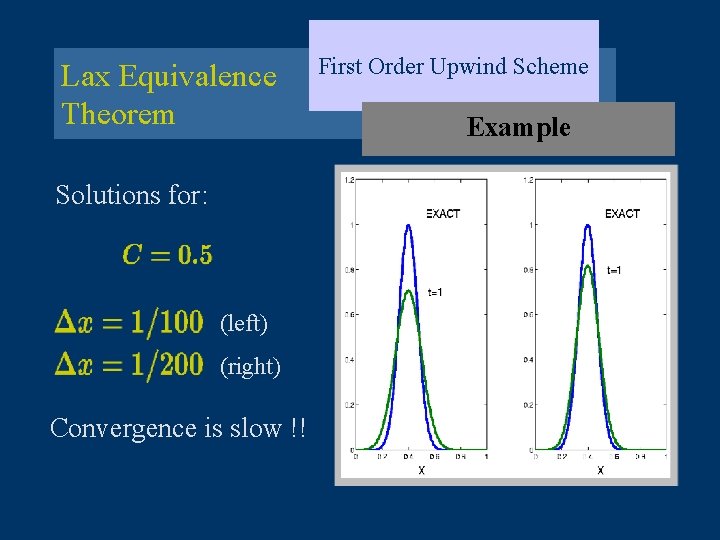
Lax Equivalence Theorem Solutions for: (left) (right) Convergence is slow !! First Order Upwind Scheme Example

CFL Condition Domains of dependence Mathematical Domain of Dependence of Set of points in where the initial or boundary data may have some effect on. Numerical Domain of Dependence of Set of points in where the initial or boundary data may have some effect on.

CFL Condition Analytical Domains of dependence First Order Upwind Scheme Numerical ( U > 0 )

CFL Condition CFL Theorem CFL Condition For each the mathematical domain of de- pendence is contained in the numerical domain of dependence. CFL Theorem The CFL condition is a necessary condition for the convergence of a numerical approximation of a partial differential equation, linear or nonlinear.

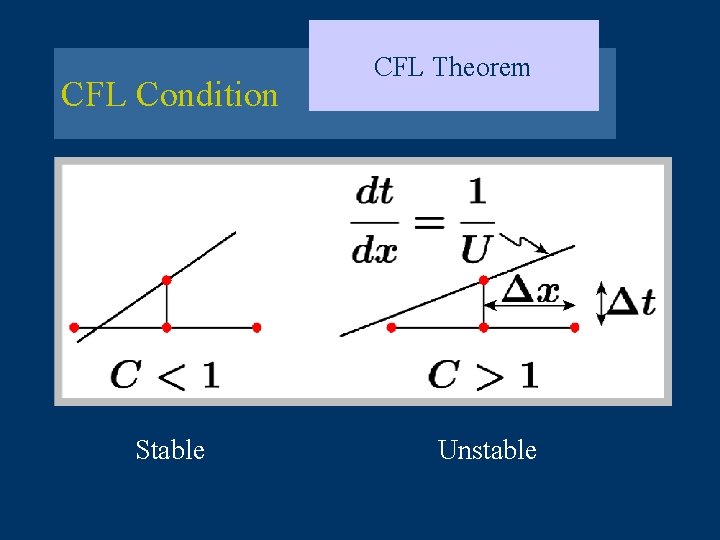
CFL Condition Stable CFL Theorem Unstable

Fourier Analysis • Provides a systematic method for determining stability → von Neumann Stability Analysis • Provides insight into discretization errors

Fourier Analysis Fourier mode: • Periodic ( period = 1 ) • Orthogonality • Eigenfunction of Continuous Problem Fourier Modes and Properties… ( integer )

Fourier Analysis Continuous Problem …Fourier Modes and Properties • Form a basis for periodic functions in • Parseval’s theorem

Fourier Analysis Continuous Problem Wave Equation

Fourier Analysis Fourier mode: k ( integer ) Discrete Problem Fourier Modes and Properties… ,

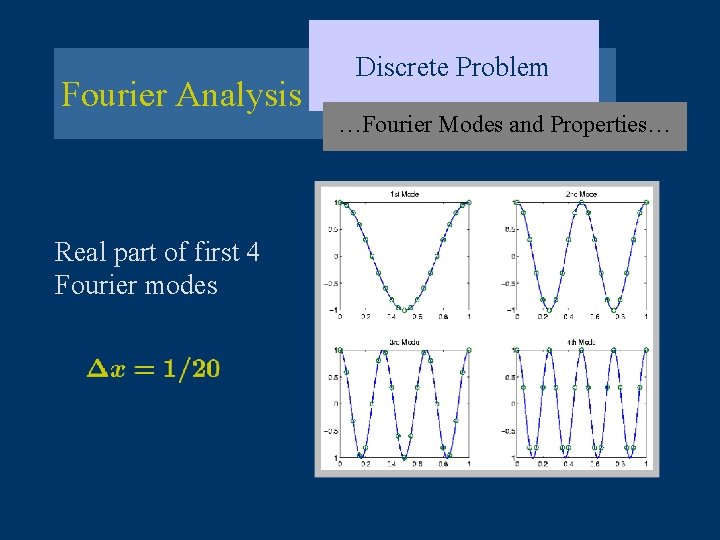
Fourier Analysis Real part of first 4 Fourier modes Discrete Problem …Fourier Modes and Properties…

Fourier Analysis • Periodic (period = J) • Orthogonality Discrete Problem …Fourier Modes and Properties…

Fourier Analysis Discrete Problem …Fourier Modes and Properties… • Eigenfunctions of difference operators e. g. ,

Fourier Analysis Discrete Problem Fourier Modes and Properties… • Basis for periodic (discrete) functions • Parseval’s theorem

Fourier Analysis Write Stability for all data von Neumann Stability Criterion

Fourier Analysis von Neumann Stability Criterion First Order Upwind Scheme…

Fourier Analysis von Neumann Stability Criterion …First Order Upwind Scheme… amplification factor Stability if which implies

Fourier Analysis Stability if: von Neumann Stability Criterion …First Order Upwind Scheme

Fourier Analysis von Neumann Stability Criterion Fourier Decomposition: FTCS Scheme…

Fourier Analysis von Neumann Stability Criterion …FTCS Scheme amplification factor Unconditionally Unstable Not Convergent

Lax-Wendroff Scheme Time Discretization Write a Taylor series expansion in time about But …

Lax-Wendroff Scheme Spatial Approximation Approximate spatial derivatives

Lax-Wendroff Scheme Equation no matrix inversion exists and is unique

Lax-Wendroff Scheme Interpretation Use Quadratic Interpolation

Lax-Wendroff Scheme Analysis Consistency Second order accurate in space and

Lax-Wendroff Scheme Insert exact solution Consistency Analysis Truncation Error into difference scheme

Lax-Wendroff Scheme Stability if: Analysis Stability

Lax-Wendroff Scheme Analysis Convergence • Consistency: • Stability: • Convergence and are constants independent of

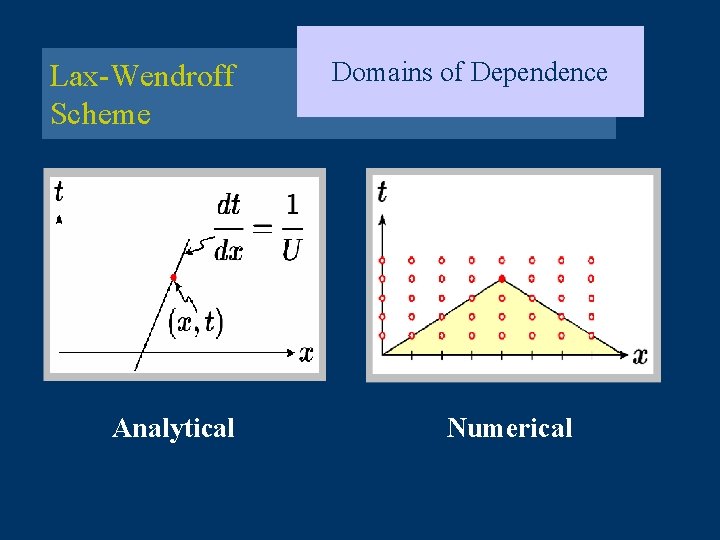
Lax-Wendroff Scheme Analytical Domains of Dependence Numerical

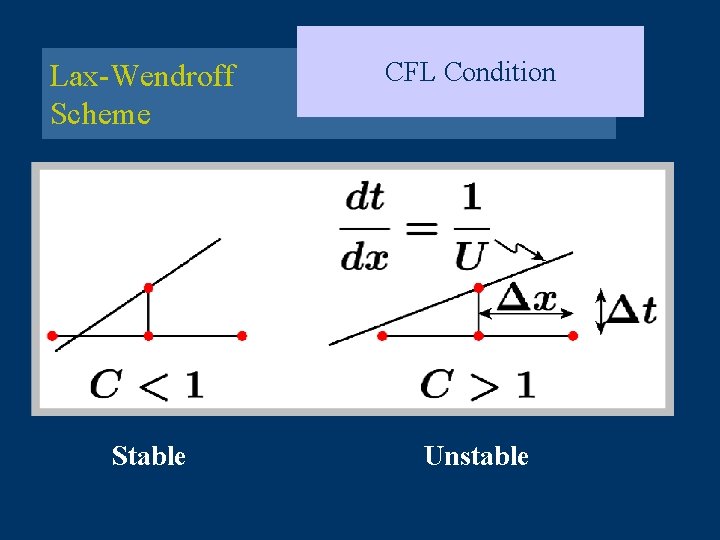
Lax-Wendroff Scheme CFL Condition Stable Unstable

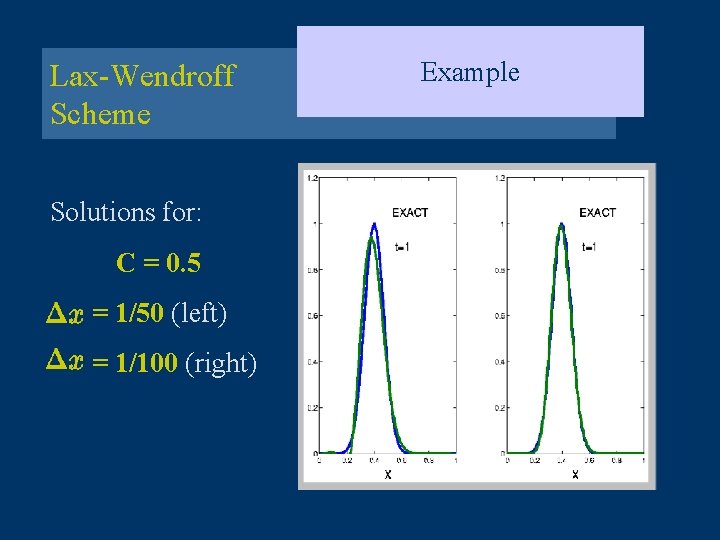
Lax-Wendroff Scheme Solutions for: C = 0. 5 = 1/50 (left) = 1/100 (right) Example

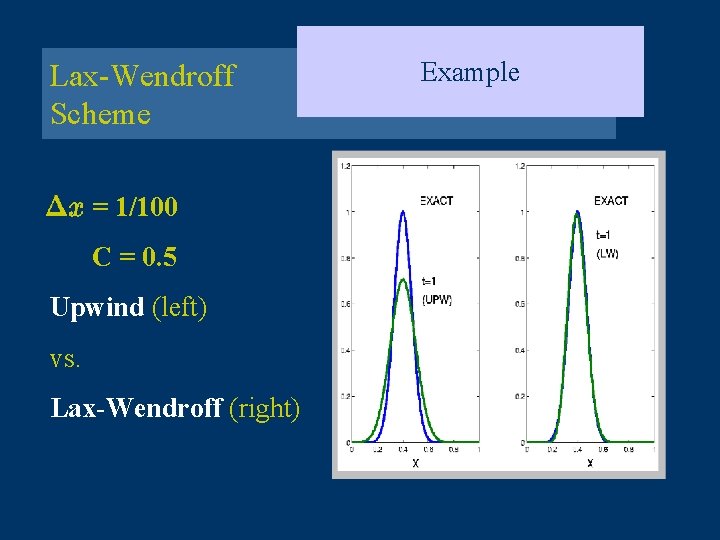
Lax-Wendroff Scheme = 1/100 C = 0. 5 Upwind (left) vs. Lax-Wendroff (right) Example

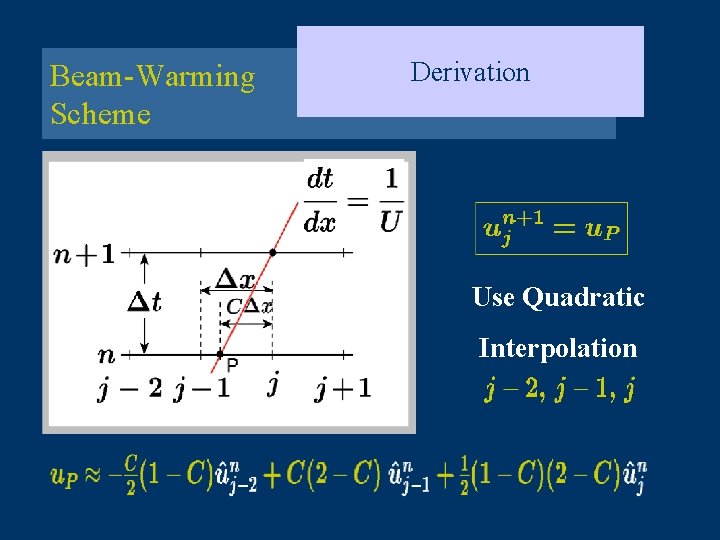
Beam-Warming Scheme Derivation Use Quadratic Interpolation

Beam-Warming Scheme • Consistency, • Stability Consistency and Stability

Method of Lines Generally applicable to time evolution PDE’s • Spatial discretization Semi-discrete scheme (system of coupled ODE’s • Time discretization (using ODE techniques) Discrete Scheme By studying semi-discrete scheme we can better understand spatial and temporal discretization errors

Method of Lines Notation approximation to vector of semi-discrete approximations;

Method of Lines Spatial Discretization Central difference … (for example) or, in vector form,

Method of Lines Spatial Discretization Fourier Analysis … Write semi-discrete approximation as inserting into semi-discrete equation

Method of Lines Spatial Discretization … Fourier Analysis … For each θ, we have a scalar ODE Neutrally stable

Method of Lines Exact solution Semi-discrete solution Spatial Discretization … Fourier Analysis …

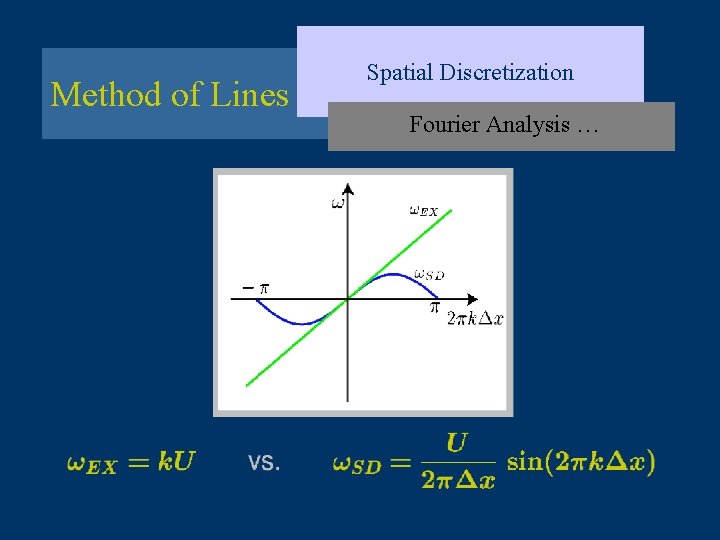
Method of Lines Spatial Discretization Fourier Analysis …

Method of Lines Time Discretization Predictor/Corrector Algorithm … Model ODE Predictor Corrector Combining the two steps you have

Method of Lines Time Discretization …Predictor/Corrector Algorithm Semi-discrete equation Predictor Corrector Combining the two steps you have

Method of Lines Fourier Stability Analysis Fourier Transform

Method of Lines Application factor with Stability Fourier Stability Analysis

Method of Lines Fourier Stability Analysis PDE Semi-discrete Discrete Semi-discrete Fourier Discrete Fourier

Method of Lines Semi-discrete Fourier semi-discrete Predictor Corrector Discrete Fourier Stability Analysis Path B …

Method of Lines Fourier Stability Analysis …Path B • Give the same discrete Fourier equation • Simpler • “Decouples” spatial and temporal discretization For each θ, the discrete Fourier equation is the result of discretizing the scalar semi-discrete ODE for the θ Fourier mode

Method of Lines Model equation: Discretization Methods for ODE’s complex- valued EF EB CN

Method of Lines Given Methods for ODE’s Absolute Stability Diagrams … and complex-valued (EF) or is defined such that (EB) or … ;

Method of Lines Methods for ODE’s …Absolute Stability Diagrams … EF EB CN

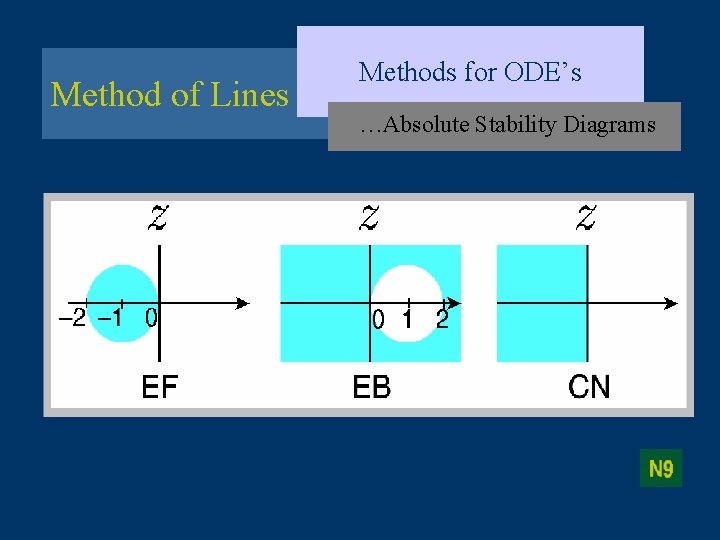
Method of Lines Methods for ODE’s …Absolute Stability Diagrams

Method of Lines Methods for ODE’s Application to the wave equation… For each Thus, • • (and ) is purely imaginary for

Method of Lines Methods for ODE’s …Application to the wave equation… EF is unconditionally unstable EB is unconditionally stable CN is unconditionally stable

Method of Lines Methods for ODE’s …Application to the wave equation… Stable schemes can be obtained by: 1) Selecting explicit time stepping algorithm which have some stability on imaginary axis 2) Modifying the original equation by adding “artificial viscosity”

Method of Lines Methods for ODE’s …Application to the wave equation… Explicit Time Stepping Scheme Predictor/Corrector

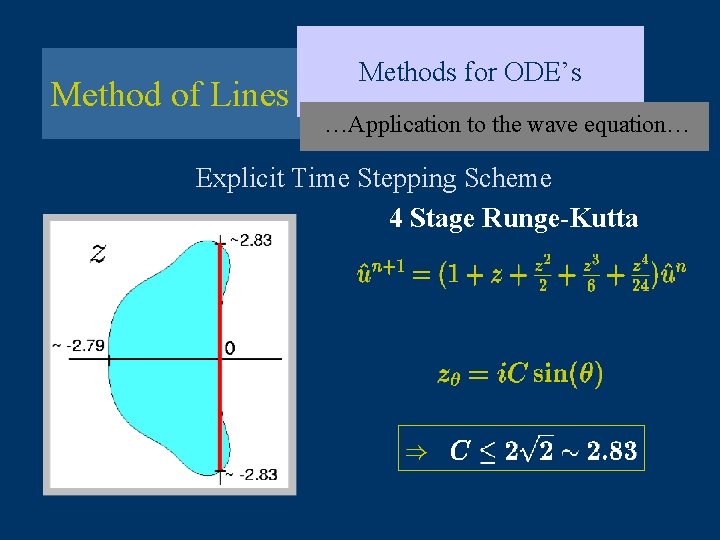
Method of Lines Methods for ODE’s …Application to the wave equation… Explicit Time Stepping Scheme 4 Stage Runge-Kutta

Method of Lines Methods for ODE’s …Application to the wave equation… Adding Artificial Viscosity Additional Term EF Time First Order Upwind Lax-Wendroff

Method of Lines Methods for ODE’s …Application to the wave equation… Adding Artificial Viscosity For each Fourier mode θ, Additional Term

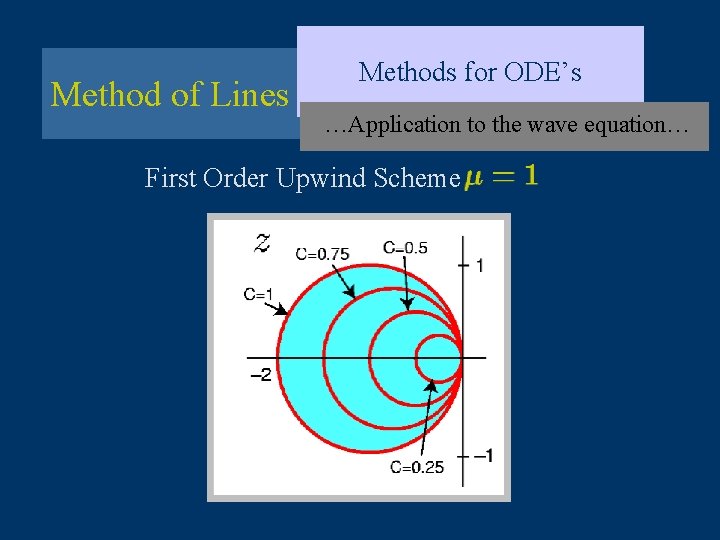
Method of Lines Methods for ODE’s …Application to the wave equation… First Order Upwind Scheme

Method of Lines Methods for ODE’s …Application to the wave equation Lax-Wendroff Scheme

Dissipation and Dispersion with Solution Model Problem and periodic boundary conditions.

Dissipation and Dispersion Model Problem represents Decay dissipation relation represents Propagation dispersion relation For exact solution of no dissipation (constant) no dispersion

Dissipation and Dispersion First Order Upwind Lax-Wendroff Beam-Warming Modified Equation

Dissipation and Dispersion • • Modified Equation For the upwind scheme dissipation dominates over dispersion Smooth solutions For Lax-Wendroff and Beam-Warming dispersion is the leading error effect Oscillatory solutions ( if not well resolved) Lax-Wendroff has a negative phase error Beaming-Warming has (for ) a positive phase error

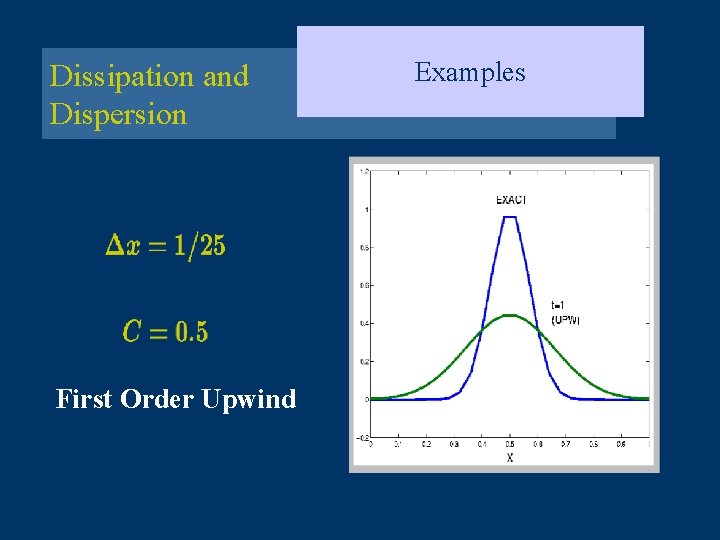
Dissipation and Dispersion First Order Upwind Examples

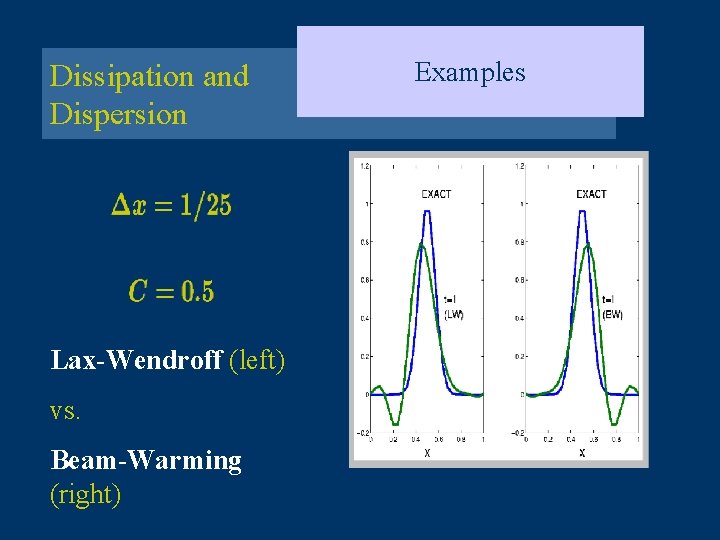
Dissipation and Dispersion Lax-Wendroff (left) vs. Beam-Warming (right) Examples

Dissipation and Dispersion Exact Discrete Relations For the exact solution , and For the discrete solution , and