Finite Difference Discretization of Elliptic Equations 1 D

Finite Difference Discretization of Elliptic Equations: 1 D Problem Lectures 2 and 3

Model Problem Poisson Equation in 1 D Boundary Value Problem (BVP) Describes many simple physical phenomena (e. g. ): • Deformation of an elastic bar • Deformation of a string under tension • Temperature distribution in a bar

Model Problem Poisson Equation in 1 D Solution Properties • The solution • • If always exists is always “smoother” then the data for all , then for all • • Given the solution is unique

Numerical Finite Differences Discretization Subdivide interval into for equal subintervals

Numerical Solution Finite Differences Approximation For example … for small

Numerical Solution Finite Differences Equations suggests …

Numerical Solution Finite Differences …. Equations (Symmetric)

Numerical Solution Finite Differences Solution Is non-singular ? For any Hence for any ( exists and is unique Is APD)

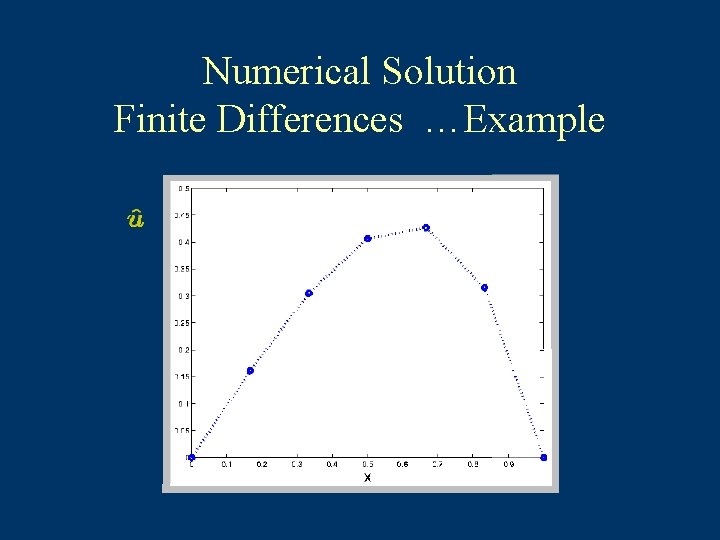
Numerical Solution Finite Differences Example… with Take

Numerical Solution Finite Differences …Example

Numerical Solution Finite Differences Convergence ? 1. Does the discrete solution retain the qualitative propeties of the continuous solution ? 2. Does the solution become more accurate when ? 3. Can we make arbierarily small ? for

Discretization Error Analysis Properties of A-1 Let • Non-negativity for • Boundedness for

Discretization Error Analysis Qualitative Properties of If for Then for

Discretization Error Analysis Qualitative Properties of Discrete Stability

Discretization Error Analysis Truncation Error For any Take we can show that

Discretization Error Analysis Error Equation Let Subtracting and be the discretization error

Discretization Error Analysis Error Equation

Discretization Error Analysis Convergence Using the discrete stability estimate on or A-priori Error Estimate

Discretization Error Analysis Numerical Example

Discretization Error Analysis Numerical Example EXAMPLE : Asymptotically,

Discretization Error Analysis Summary • For a simple model problem we can produce numerical approximations of arbitrary accuracy. • An a-priori error estimate gives the asymptotic dependence of the solution error on the discretization size.

Generalizations Definitions Consider a linear elliptic differential equation and a difference scheme

Generalizations Consistency The difference scheme is consistent with the differential equation if: For all smooth functions for when for all is order of accuracy

Generalizations Truncation Error for or, The truncation error results from inserting the exact solution into the difference scheme. Consistency

Generalizations Error Equation Original scheme Consistercy The error satisfies

Generalizations Stability Matrix norm The difference scheme is stable if (independent of )

Generalizations Stability (max row sum)

Generalizations Convergence Error equation Taking norms

Generalizations Summary Consistency + Stability Convergence Stability Consistency

The Eigenvalue Problem Model Problem Statement Find nontrivial denote solutions such that with

The Eigenvalue Problem Application Axially Loaded Beam • “Small” Deflection • External Force Equilibrium

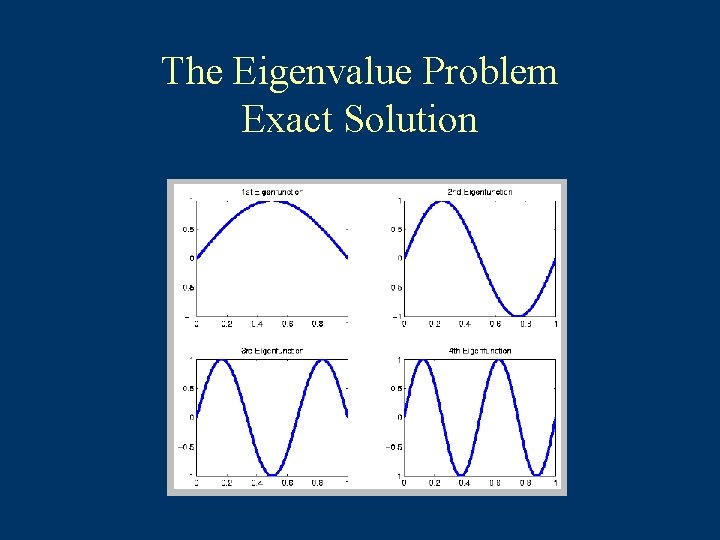
The Eigenvalue Problem Exact Solution or

The Eigenvalue Problem Exact Solution Thus (choose Larger ) more oscillatory larger

The Eigenvalue Problem Exact Solution

The Eigenvalue Problem Discrete Equations Difference Formulas

The Eigenvalue Problem Discrete Equations Matrix Form

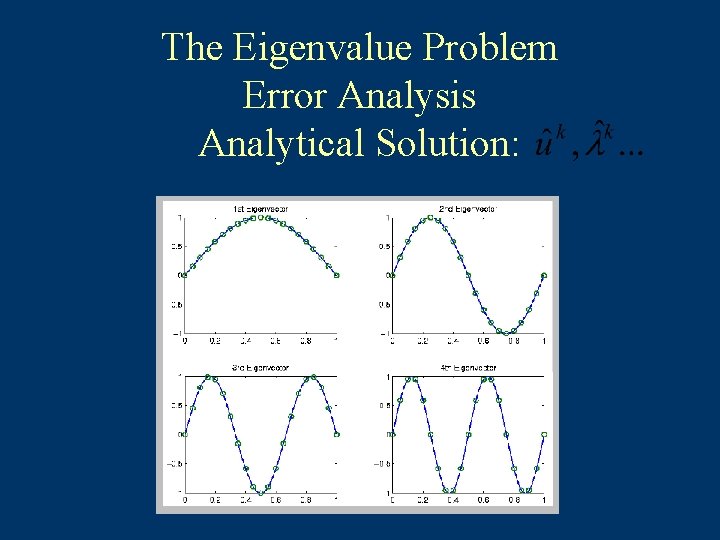
The Eigenvalue Problem Error Analysis Analytical Solution: Claim that Note since

The Eigenvalue Problem Error Analysis Analytical Solution:

The Eigenvalue Problem Error Analysis Analytical Solution: What are ?

The Eigenvalue Problem Error Analysis Analytical Solution: Thus:

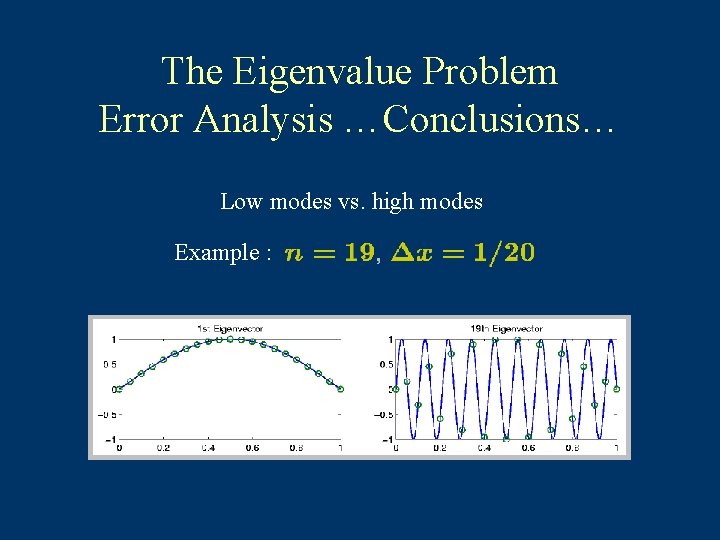
The Eigenvalue Problem Error Analysis Conclusions… Low modes For fixed , : second-order convergence

The Eigenvalue Problem Error Analysis …Conclusions… High modes : For as High modes ( ) are not accurate.

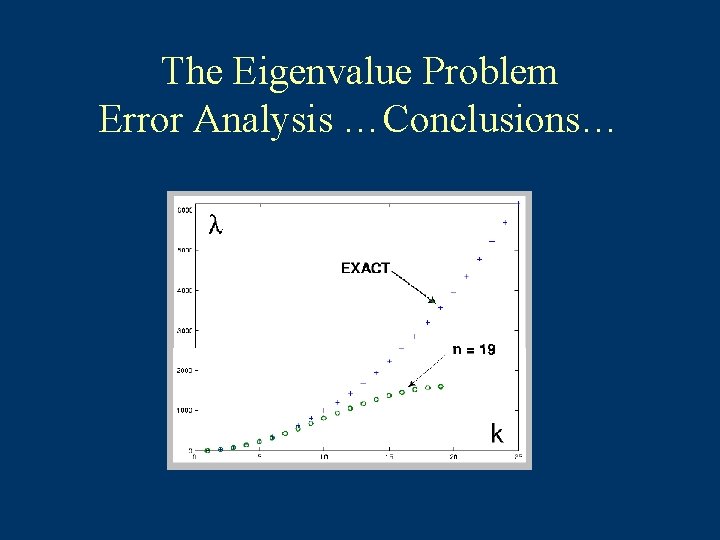
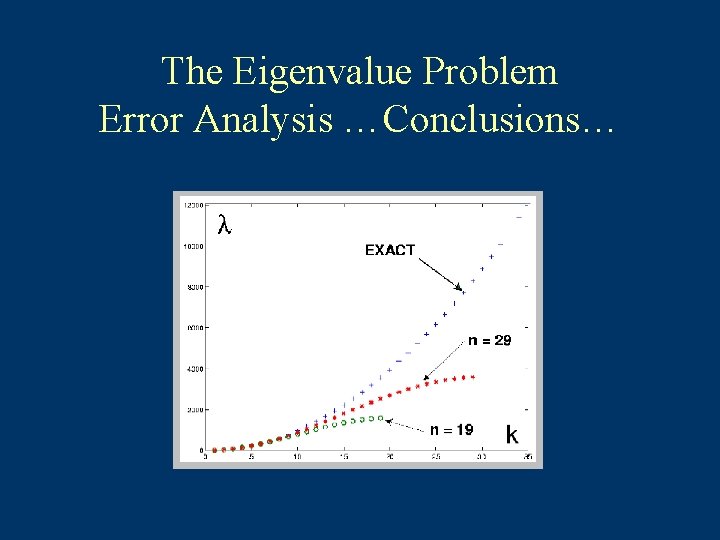
The Eigenvalue Problem Error Analysis …Conclusions… Low modes vs. high modes Example :

The Eigenvalue Problem Error Analysis …Conclusions… Low modes vs. high modes resolved not resolved accurate not accurate is BUT: as , , so any fixed mode converges.

The Eigenvalue Problem Error Analysis …Conclusions…

The Eigenvalue Problem Error Analysis …Conclusions…

The Eigenvalue Problem Condition Number of A For a SPD matrix given by = Thus, for our , the condition number is maximum eigenvalue of minimum eigenvalue of matrix, as grows (in ) as number of grid points squared. Importance: understanding solution procedures.

The Eigenvalue Problem Link to …Discretization… Recall : or

The Eigenvalue Problem Link to …Discretization… Error equation : for as (consistency)

The Eigenvalue Problem Link to Norm Discretization We will use the “modified” norm for Thus, from consistency

The Eigenvalue Problem Link to ||. || Discretization… Ingredients: 1. Rayleigh Quotient : for all 2. Cauchy-Schwarz Inequality : for all

The Eigenvalue Problem Link to ||. || Discretization… Convergence proof:

The Eigenvalue Problem Link to ||. || Discretization…

The Eigenvalue Problem Link to ||. || Discretization… Since From error equation Multiplying by Alternative Derivation