Finite Deference Method by Dr Samah Mohamed Mabrouk

Finite Deference Method by Dr. Samah Mohamed Mabrouk www. smmabrouk. faculty. zu. edu. eg 1

Difference equations for the Laplace and Poisson equations Poisson’s equation Where is the Laplacian operator Laplace’s equation SE 301_Topic 6 Al-Amer 2005 2

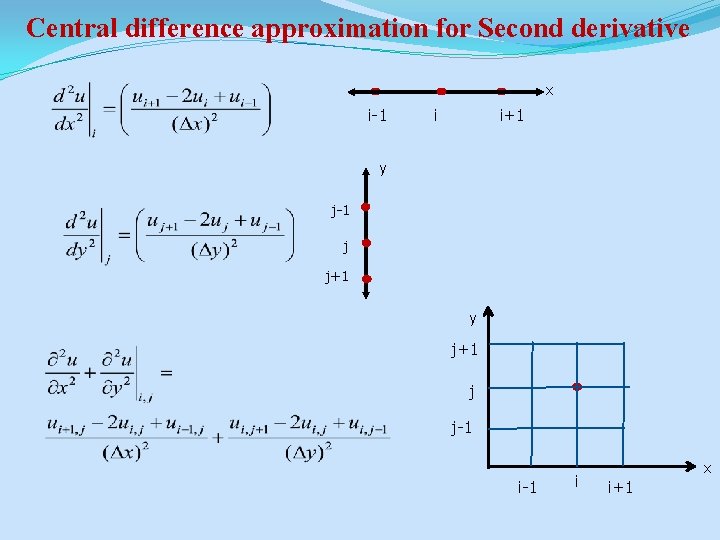
Central difference approximation for Second derivative x i-1 i i+1 y j-1 j j+1 y j+1 j j-1 i x i+1

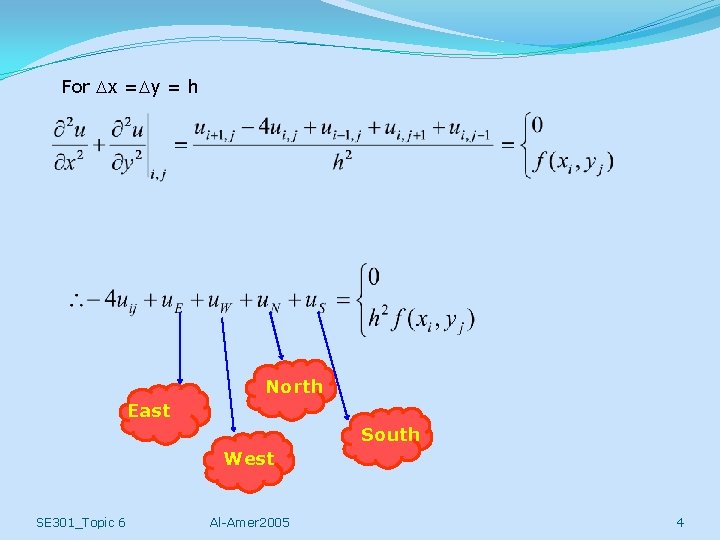
For x = y = h North East South West SE 301_Topic 6 Al-Amer 2005 4

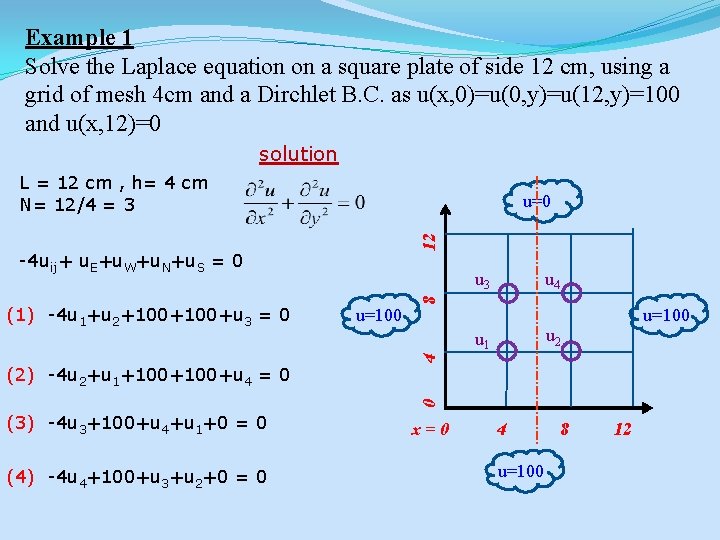
Example 1 Solve the Laplace equation on a square plate of side 12 cm, using a grid of mesh 4 cm and a Dirchlet B. C. as u(x, 0)=u(0, y)=u(12, y)=100 and u(x, 12)=0 solution L = 12 cm , h= 4 cm N= 12/4 = 3 12 u=0 -4 uij+ u. E+u. W+u. N+u. S = 0 u 4 8 (1) -4 u 1+u 2+100+u 3 = 0 u 3 u=100 u 2 4 u 1 0 (2) -4 u 2+u 1+100+u 4 = 0 (3) -4 u 3+100+u 4+u 1+0 = 0 (4) -4 u 4+100+u 3+u 2+0 = 0 x=0 4 u=100 8 12

In matrix form Au=b But the problem is symmetry, u 1 =u 2 and u 3 =u 4 So we can solve only for u 1 and u 3 (1) -4 u 1+u 2+100+u 3 = 0 (3) -4 u 3+100+u 4+u 1+0 = 0 Then replace for u 1 =u 2 and u 3 =u 4, the system of equations is reduced to -3 u 1 +u 3 = -200 u 1 -3 u 3 = -100 SE 301_Topic 6 Which has a solution u 1 =u 2 =87. 5 and u 3 =u 4 =62. 5 Al-Amer 2005 6

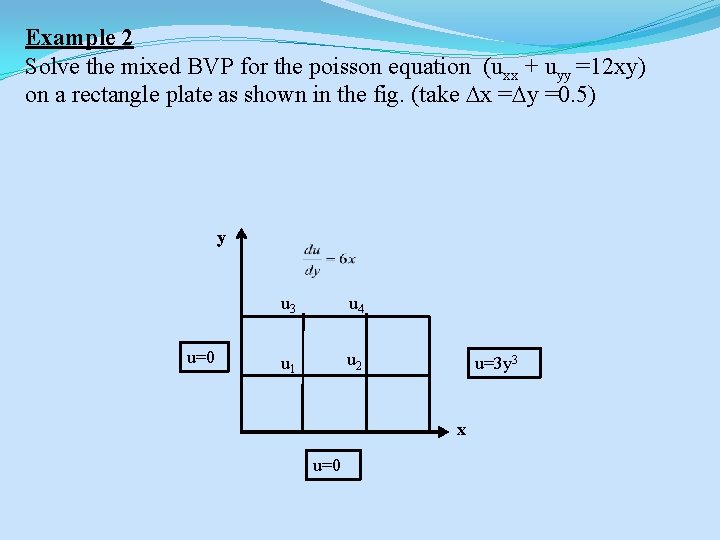
Example 2 Solve the mixed BVP for the poisson equation (uxx + uyy =12 xy) on a rectangle plate as shown in the fig. (take x = y =0. 5) y u=0 u 3 u 4 u 1 u 2 u=3 y 3 x u=0

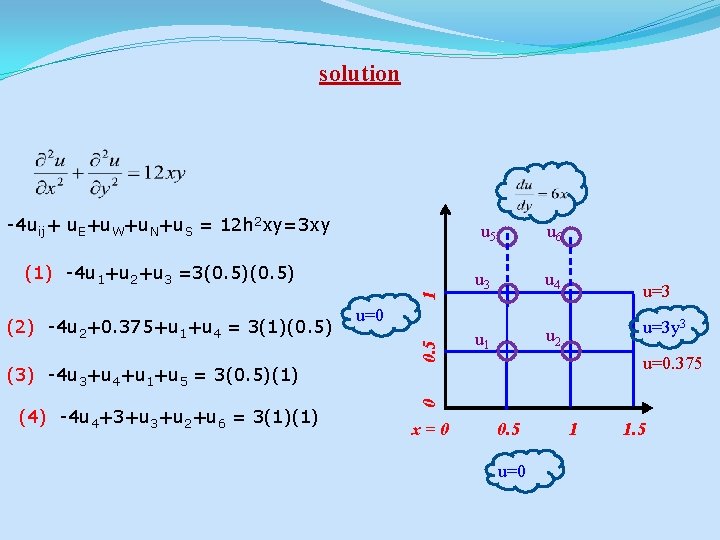
solution -4 uij+ u. E+u. W+u. N+u. S = 12 h 2 xy=3 xy u 5 1 (1) -4 u 1+u 2+u 3 =3(0. 5) u 3 u 4 u=3 u=0 0. 5 (2) -4 u 2+0. 375+u 1+u 4 = 3(1)(0. 5) u 6 u=3 y 3 u 2 u 1 u=0. 375 (4) -4 u 4+3+u 2+u 6 = 3(1)(1) 0 (3) -4 u 3+u 4+u 1+u 5 = 3(0. 5)(1) x=0 0. 5 u=0 1 1. 5

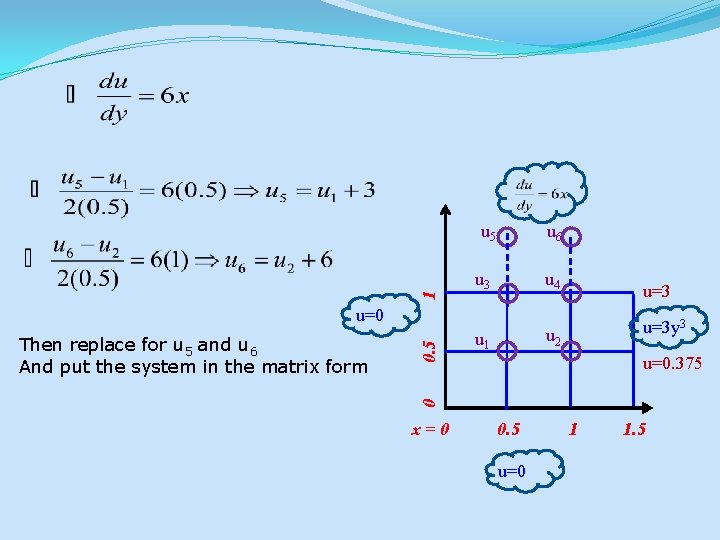
1 u 5 u 6 u 3 u 4 u=3 y 3 u 2 u 1 u=0. 375 0 Then replace for u 5 and u 6 And put the system in the matrix form 0. 5 u=0 x=0 0. 5 u=0 1 1. 5

Which has a solution SE 301_Topic 6 Al-Amer 2005 10

EXERCISE For a rectangle thin plate of dimension 4*3 units, u(x, 0)=u(x, 3)=10 x, u(0, y)=0 and u(4, y)= 40 +10 y(y-3). Solve the Poisson’s equation 2 = 5 x , take x = y = 1

EXERCISES