Finite Automata State Transition Graph Nondeterministic FA DFA

Finite Automata State Transition Graph (Non)deterministic FA: DFA, NFA Regular Expression Myhill-Nerode’s Theorem State Minimization Pumping Lemma

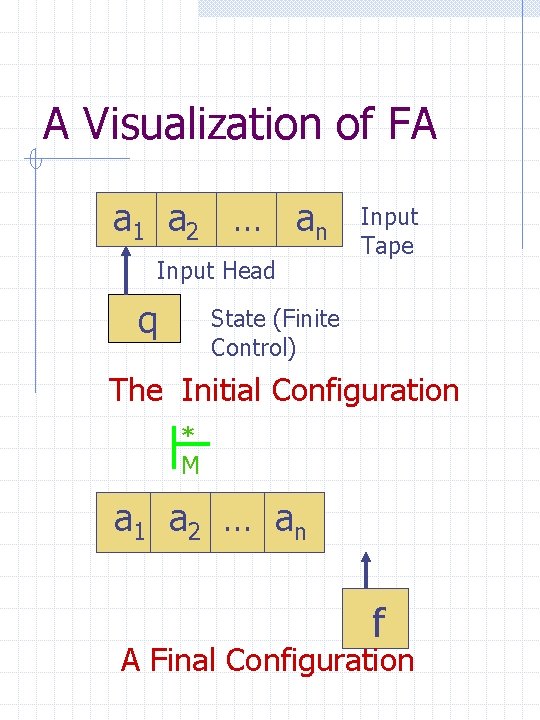
A Visualization of FA a 1 a 2 … a n Input Head q Input Tape State (Finite Control) The Initial Configuration * M a 1 a 2 … a n f A Final Configuration

Finite Automaton M=(Q, Σ, δ, q 0, F) Quadruple Representation Q: the set of states (finite alphabet) Σ: the set of input symbols (finite alphabet) δ: Q Σ Q the state transition function q 0 Q: the initial state F Q: the set of final states (accepting states)

State Transition Table M=({q 0, q 1, q 2}, {0, 1}, q 0, δ, F) δ(q 0, 0)=q 0, δ(q 0, 1)=q 1, δ(q 1, 0)=q 1, δ(q 1, 1)=q 2, δ(q 2, 0)=q 2, δ(q 2, 1)=q 0. STT q 0 q 1 q 2 1 q 2 q 0 accepting state initial state

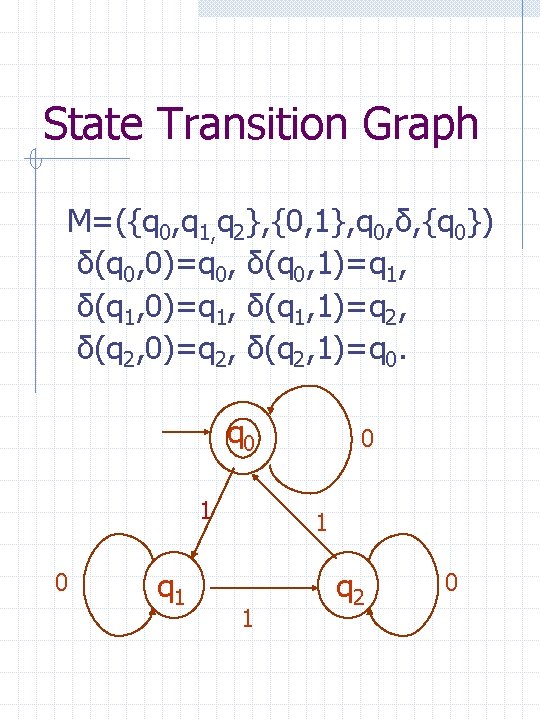
State Transition Graph M=({q 0, q 1, q 2}, {0, 1}, q 0, δ, {q 0}) δ(q 0, 0)=q 0, δ(q 0, 1)=q 1, δ(q 1, 0)=q 1, δ(q 1, 1)=q 2, δ(q 2, 0)=q 2, δ(q 2, 1)=q 0. q 0 1 0 q 1 0 1 1 q 2 0

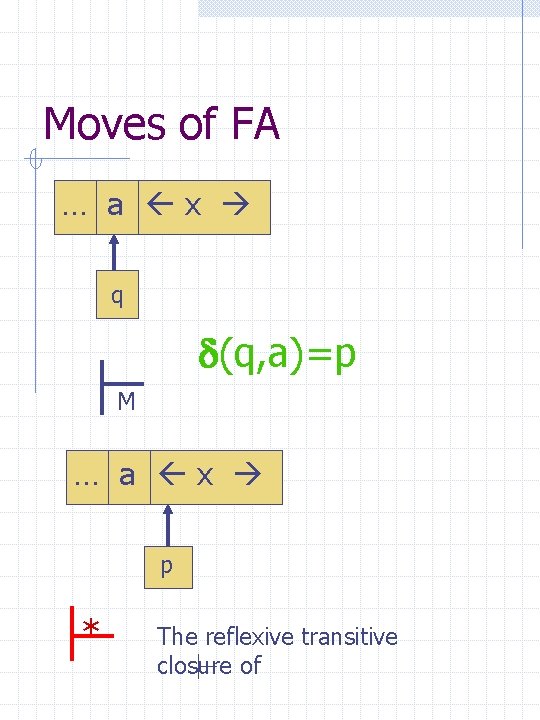
Moves of FA … a x q (q, a)=p M … a x p * The reflexive transitive closure of

Accepted Languages x L(M) x is accepted by M Û (q 0, x) |* (f, ), f F Û *(q 0, x) F where (q, ax) | (p, x) if (q, a)=p and *(q, )=q for any q Q, *(q, xa)= ( *(q, x), a) for q Q, a , x *. M accepts the language L(M) = {x * | M accepts x}

Deterministic and Nondeterministic FAs DFA M=(Q, , , q 0, F), where : Q Q. NFA M=(Q, , , q 0, F), where : Q 2 Q. *: Q * 2 Q is defined by *(q, )={q} *(q, xa)= ( *(q, x), a) L(M)={w * | *(q 0, w) F }

Equivalence of DFAs and NFAs THEOREM L(DFA)=L(NFA), where L(a class of devices D) ={the language defined by M | M in D}. Proof: L(DFA) L(NFA) is trivial. To prove L(NFA) L(DFA), construct the DFA M’ for each NFA M s. t. L(M’)=L(M): If M=(Q, , , q 0, F), then let M’=(Q’, , ’, q’ 0, F’), where Q’=2 Q, q’ 0={q 0}, F’={q’ Q’ | q’ F }, ’(q’, a)= (q’, a) for q’ Q’ and a .

Algorithm: From an NFA to an equivalent DFA 1. Let the state on the 1 st line of 2. 3. 4. 5. 6. the STT be q’ 0={q 0}. Put in front of q’ 0 if q 0 F. n 1; m 1. Fill in the blank entries on the n-th line. Each time a new state is produced, add it on the (m+1)-th line and increment m by 1; Put in front of the new state if it contains a state in F. Increment n by 1. If the n-th line is complete, halt. Otherwise, go to line 4.

NFA with -Moves M=(Q, , , q 0, F), where : Q ( { }) 2 Q. *(q, )= {q} for any q Q, *(q, xa)= ( *(q, x), a) for q Q, a , x *, where for P Q, P={q | pi+1 (pi, ) for 0 i<k, p 0=p P, pk=q}. L(M)={w * | *(q 0, w) F }

Algorithm -NFAto. DFA : From an -NFA to an equivalent DFA 1. q’ 0 {q 0}; Q’ {q’ 0}. If *(q 0, ) contains a state in F, let q’ 0 be in F’. 2. If q’ Q’, a , and ’(q’, a) is not yet determined, then let ’(q’, a)= *(q’, a). If this *(q’, a) is not yet in Q’, then add it to Q’, and let it be in F’ also if it contains a state in F. 3. If ’(q’, a) is already defined for each q’ Q’ and a , then halt; Otherwise go to line 2.

Two-Way NFAs (2 NFA) M=(Q, , , q 0, F), where : Q 2 Q {-1, 0, 1}. ID (Instantaneous Description) (q, x, i) (p, x, i+d) iff (p, d) (q, x[i]), where x ¢ *$, 1 i+d |x|, x[i] denotes the ith symbol of x. L(M)={w * | (q 0, ¢w$, 1) * (f, ¢w$, i), f F, 1 i |¢w$|} THEOREM L(2 NFA)=L(NFA).