Finite Automata Finite State Machines and Tokenizing Tokenization

Finite Automata (Finite State Machines) and Tokenizing

Tokenization • The first step in document processing • Divides the document into tokens, or smallest meaningful units • Creates a set of terms from which index terms are selected • Theory end of things: tokenizing is equivalent to specifying a DFA, which recognizes a regular language

Theory • Languages are defined by grammars • Scanner/recognizer: A program that takes a stream of characters (tokens) and determines • “is this sequence in the language defined by the grammar: yes? no? ”

Chomsky Hierarchy • Regular expressions • Finite Automata, Deterministic FA (DFA), Finite State Machine (FSM) (flex) • Markov models: NFA with probabilities on the links • Context free languages (programming languages) • Push down automata Expression = factor | factor Expression • Context sensitive languages • Linearly bounded Turing Machine • Natural Language • Human Brain • Unbounded Turing Machine

Regular expressions • A regular expression is defined (recursively) as: • A character • The empty string, ε • 2 regular expressions concatenated • a b* : ab abbbbbb a • 2 regular expressions connected by an “or”, usually written x | y • 0 or more copies of a regular expression – written *, and called the Kleene star

Another view: DFAs • Regular languages are also precisely the set of strings that can be accepted by a deterministic finite automata (DFA) • Formally, a DFA is: • a set of states q 0…. q. N • an input alphabet a. . z. A. . Z 0. . 9 • a start state q 0 • a set of accept (final) states (q 5, q 17, q 22) • a transition function: given a state and input, outputs another state (q 0, a, q 18; …. )

DFAs • More often, we’ll just draw a picture (like in graph theory) • Example:

DFA examples • What’s the DFA for the regular language: 1(0|1)*0 • What’s the regular language accepted by this DFA?

NFAs • Nondeterministic finite automata (NFA) are a variant of DFAs. • DFAs do not allow for any ambiguity: • if a character is read, there can only be 1 arrow showing where to go • No empty string transitions, so must read a character in order for the transition function to move to a new state • If instead we have multiple options, it is called an NFA

NFA Examples • What do the following NFAs accept?

More NFAs • Some things are easier with NFAs than DFAs: unsigned_number -> unsigned_int (ε |. unsigned_int) unsigned_int -> [0 -9]

NFAs • Essentially, when parsing a stream of characters, we can think of an NFA as modeling a parallel set of possibilities • Theorem: Every NFA has an equivalent DFA. • (And so both recognize regular languages, even though NFAs seem more powerful. ) • Can therefore convert any NFA into a DFA

Why do we care? • When defining a tokenizer, we usually start with a set of regular expressions. • We (flex etc) create a DFA for each regular expression • Combining them creates an NFA • Then, convert the NFA to a DFA • Finally, modify DFA to minimize it, make it smaller, more efficient

Coding DFAs (scanners) • So, given a DFA, code can be implemented in 2 ways: • A bunch of if/switch/case statements • A table and driver • Flex uses the second approach

Scanners/Recognizer • Writing a pure DFA as a set of nested case statements is a surprisingly useful programming technique • though it's often easier to use perl, awk, sed, python, regular expression libraries, • Table-driven DFA is what flex produces • lex (flex) in the form of C or C++

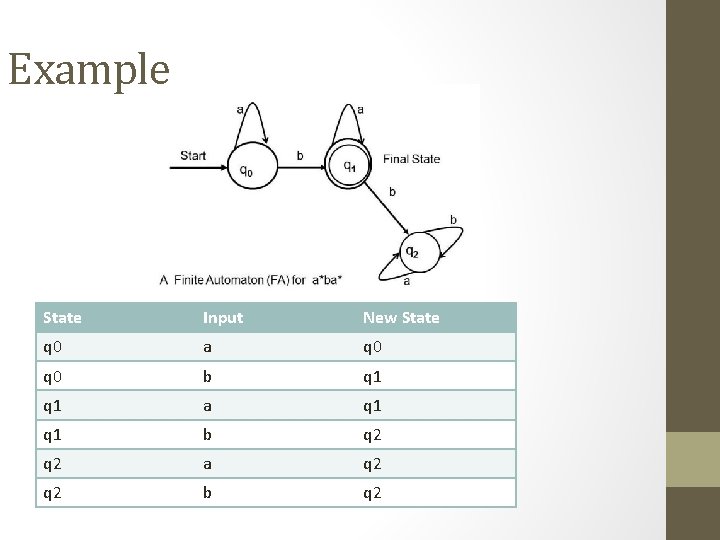
Example State Input New State q 0 a q 0 b q 1 a q 1 b q 2 a q 2 b q 2

Complexity • Recognizer: • Read next character • Go to next state • Perform optional action (flex) • Complexity • O(c) where c is the number of characters in the document • Linear in the number of characters in the document • Optimally efficient • Just reading the document is O(c ) so this as as efficient as possible