Fingerprint Matching Algorithm by Unit Circle Parameterization What

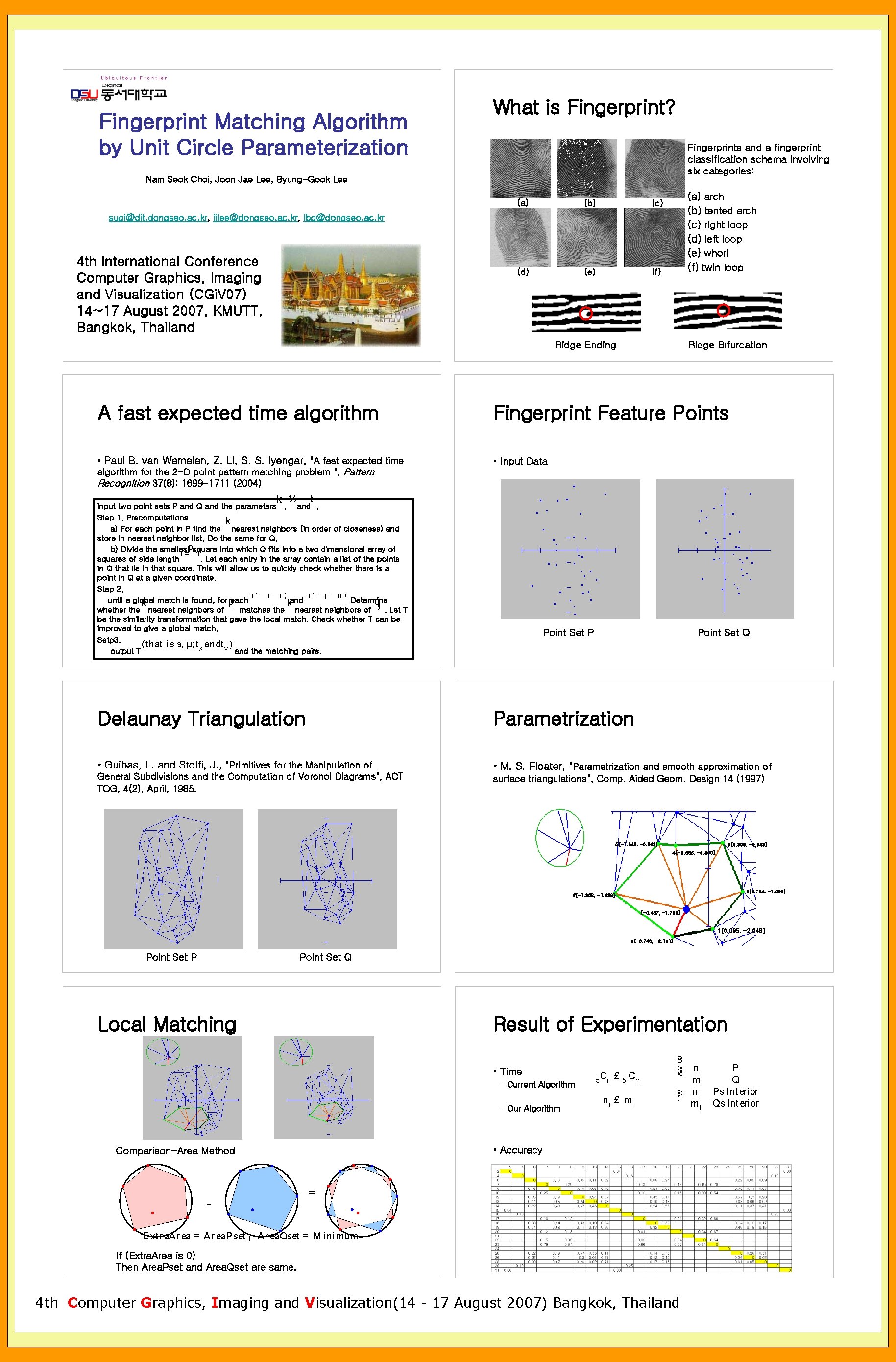
Fingerprint Matching Algorithm by Unit Circle Parameterization What is Fingerprint? Fingerprints and a fingerprint classification schema involving six categories: Nam Seok Choi, Joon Jae Lee, Byung-Gook Lee (a) (b) (c) (d) (e) (f) (a) arch (b) tented arch (c) right loop (d) left loop (e) whorl (f) twin loop sugi@dit. dongseo. ac. kr, jjlee@dongseo. ac. kr, lbg@dongseo. ac. kr 4 th International Conference Computer Graphics, Imaging and Visualization (CGi. V 07) 14~17 August 2007, KMUTT, Bangkok, Thailand Ridge Ending Ridge Bifurcation A fast expected time algorithm Fingerprint Feature Points • Paul B. van Wamelen, Z. Li, S. S. Iyengar, "A fast expected time algorithm for the 2 -D point pattern matching problem ", Pattern Recognition 37(8): 1699 -1711 (2004) • Input Data k ½ t input two point sets P and Q and the parameters , and. Step 1. Precomputations k a) For each point in P find the nearest neighbors (in order of closeness) and store in nearest neighbor list. Do the same for Q. b) Divide the smallestpsquare into which Q fits into a two dimensional array of r= n squares of side length. Let each entry in the array contain a list of the points in Q that lie in that square. This will allow us to quickly check whethere is a point in Q at a given coordinate. Step 2. i (1 · i · n) j (1 · j · m) until a global match is found, for each and Determine p qj k k i whether the nearest neighbors of matches the nearest neighbors of. Let T be the similarity transformation that gave the local match. Check whether T can be improved to give a global match. Setp 3. (t hat is s, µ; t x andt y ) output T and the matching pairs. Point Set Q Point Set P Delaunay Triangulation Parametrization • Guibas, L. and Stolfi, J. , "Primitives for the Manipulation of • M. S. Floater, "Parametrization and smooth approximation of surface triangulations", Comp. Aided Geom. Design 14 (1997) General Subdivisions and the Computation of Voronoi Diagrams", ACT TOG, 4(2), April, 1985. 5[-1. 048, -0. 562] 3[0. 305, -0. 543] 4[-0. 686, -0. 600] 2[0. 724, -1. 400] 6[-1. 962, -1. 438] [-0. 457, -1. 705] 1[0. 095, -2. 048] 0[-0. 743, -2. 181] Point Set Q Point Set P Local Matching Result of Experimentation • Time – Current Algorithm – Our Algorithm 5 Cn £ 5 Cm ni £ mi 8 > > < n m ni > > : mi • Accuracy Comparison-Area Method = - E xtr a. Ar ea = Ar ea. P set ¡ Ar ea. Qset = M i ni mum If (Extra. Area is 0) Then Area. Pset and Area. Qset are same. 4 th Computer Graphics, Imaging and Visualization(14 - 17 August 2007) Bangkok, Thailand P Q Ps Int erior Qs Int erior