Finding the Sum of the Interior Angles of


















- Slides: 21

Finding the Sum of the Interior Angles of a Convex Polygon Fun with Angles Mrs. Ribeiro’s Math Class

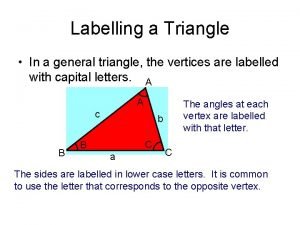
Review Terms n Polygons n Convex and Concave Polygons n Vertex (pl. Vertices)

Polygons A plane shape (two-dimensional) with straight sides. Examples: triangles, rectangles and pentagons. Note: a circle is not a polygon because it has a curved side

Types of Polygons

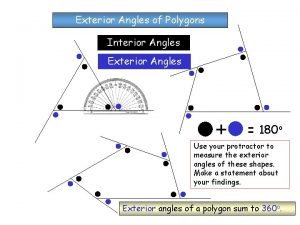
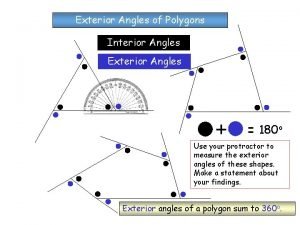
Convex Polygon A convex polygon has no angles pointing inwards. More precisely, no internal angles can be more than 180°.

Concave Polygon If there any internal angles greater than 180° then it is concave. (Think: concave has a "cave" in it)

Review Terms n Side n Adjacent v. Opposite n Diagonals

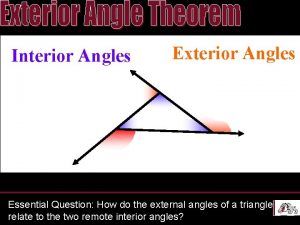
Review Concepts n n What is the sum of the interior angles of a triangle? How can we use this to find missing angles in a triangle? a + b + c = 180º

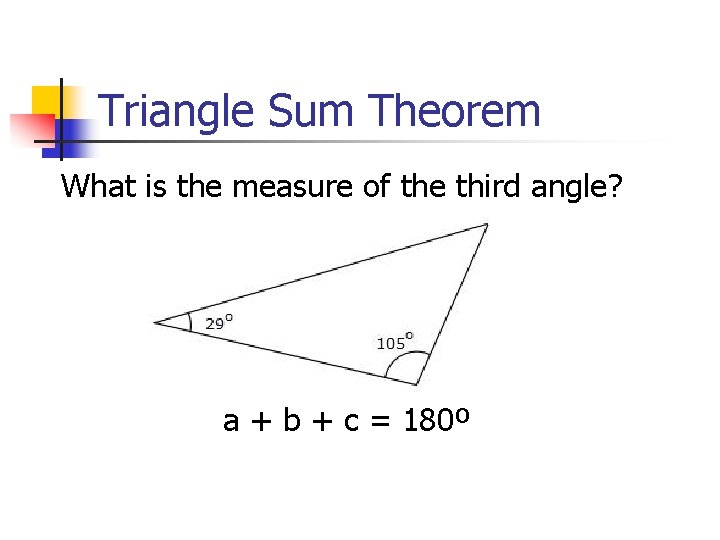
Triangle Sum Theorem What is the measure of the third angle? a + b + c = 180º

Triangle Sum Theorem The measure of the third angle is: The interior angles of a triangle add to 180° The sum of the given angles = 29° + 105° = 134° Therefore third angle = 180° - 134° = 46°

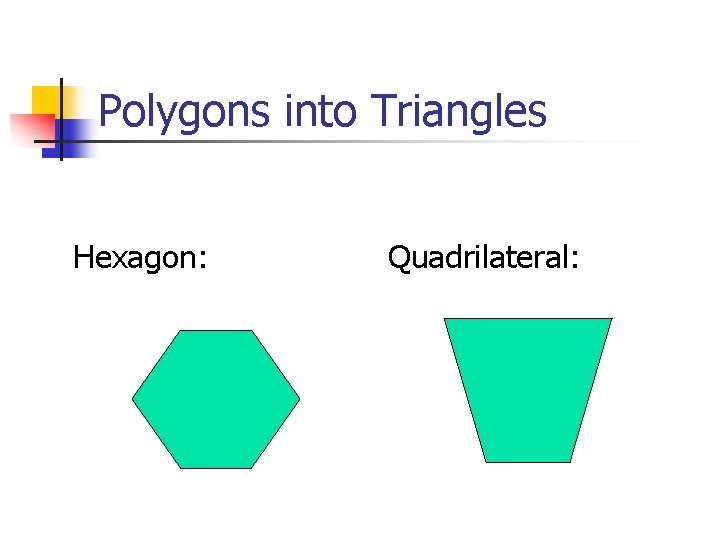
Divide a Polygon into Triangles n n n Choose a vertex Draw a diagonal to the closest vertex at left that is not adjacent Repeat for additional diagonals until you reach the adjacent at right

Polygons into Triangles Hexagon: Quadrilateral:

Polygons into Triangles n n Let’s count triangles!… Hexagon: Quadrilateral

Rule for Convex Polygons Sum of Internal Angles = (n-2) × 180° Measure of any Angle in Regular Polygon = (n-2) × 180° / n


Example: A Regular Decagon Sum of Internal Angles = (n-2) × 180° (10 -2)× 180° = 8× 180° = 1440° Each internal angle (regular polygon) = 1440°/10 = 144°

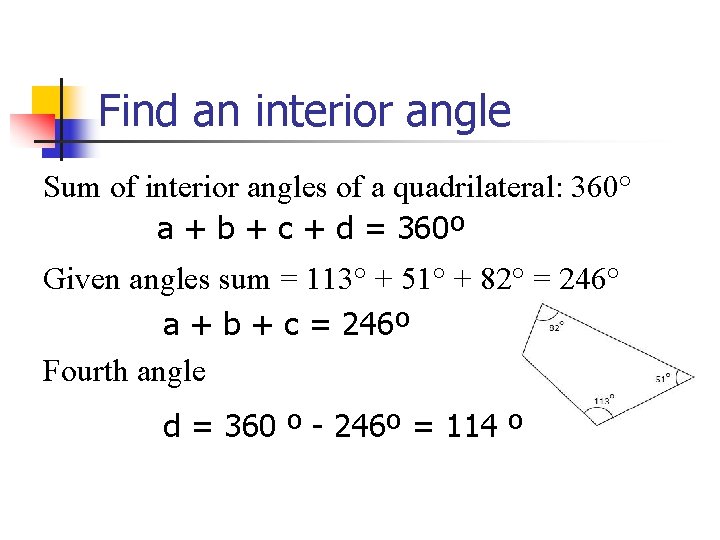
Find an interior angle What is the fourth interior angle of this quadrilateral? A 134° B 129° C 124° D 114° Use pencil and paper – work with a shoulder partner

Find an interior angle Sum of interior angles of a quadrilateral: 360° a + b + c + d = 360º Given angles sum = 113° + 51° + 82° = 246° a + b + c = 246º Fourth angle d = 360 º - 246º = 114 º

Working “Backwards” Each of the interior angles of a regular polygon is 156°. How many sides does this polygon have? A 15 B 16 C 17 D 18

Working “Backwards” Use the formula for one angle of a regular n-sided polygon. We know one angle = 156° Now we solve for "n": Multiply both sides by n ⇒ (n - 2) × 180 = 156 n Expand (n-2) ⇒ 180 n - 360 = 156 n Subtract 156 n from both sides: ⇒ 180 n - 360 - 156 n = 0 Add 360 to both sides: ⇒ 180 n - 156 n = 360 Subtract 180 n-156 n ⇒ 24 n = 360 Divide by 24 ⇒ n = 360 ÷ 24 = 15

References n n Johnson, Lauren. (27 April 2006). “Polygons and their interior angles. ” University of Georgia. Retrieved (04 Dec. 2011) from http: //intermath. coe. uga. edu/tweb/gcsu-geospr 06/ljohnson/geolp 2. doc. Kuta Software LLC. (2011). “Introduction to Polygons” Infinite Geometry. Retrieved (04 Dec. 2011) from <http: //www. kutasoftware. com/Free. Worksheets/Geo. Worksheets/6 Introduction%20 to%20 Polygons. pdf> Mathopolis. com (2011) “Question 1780 by lesbillgates. ” Retrieved (0 Dec. 2011) from <http: //www. mathopolis. com/questions/q. php? id=1780&site=1&ref=/geometry/interior-anglespolygons. html&qs=825_826_827_828_1779_829_1780> Pierce, Rod. (2010). “Interior Angles of Polygons. ” Mathsis. Fun. com. Retrieved (04 Dec. 2011) from <http: //www. mathsisfun. com/geometry/interior-angles-polygons. html>
 Regular dodecagon exterior angles
Regular dodecagon exterior angles Convex polygon formula
Convex polygon formula Polygons and quadrilaterals
Polygons and quadrilaterals Sum of a triangle
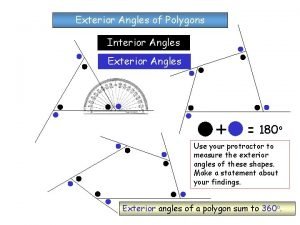
Sum of a triangle Measure of polygon exterior angles
Measure of polygon exterior angles Exterior angle of octagon
Exterior angle of octagon Sum of exterior angles
Sum of exterior angles Sum of interior angles of a polygon
Sum of interior angles of a polygon Polygons formula
Polygons formula Neverangles
Neverangles Opposite angles
Opposite angles What is the name of this polygon?
What is the name of this polygon? A polygon with an interior angle sum of 1260
A polygon with an interior angle sum of 1260 Sum0
Sum0 Finding the measure of an angle
Finding the measure of an angle How to find length of side of triangle using angles
How to find length of side of triangle using angles Cosine rule for obtuse angles
Cosine rule for obtuse angles When do we use sine rule
When do we use sine rule How to solve inverse trig functions
How to solve inverse trig functions Reference angle of 315
Reference angle of 315 Classifying quadrilaterals worksheet
Classifying quadrilaterals worksheet Sine rule notes
Sine rule notes