Finding the Magnitude and Direction of the Resultant

Find the Magnitude Using the Pythagorean Theorem § The Pythagorean theorem is a useful

Example Problem § Eric leaves the base camp and hikes 11 km, north and

YOUR TURN. . … Find the magnitude of the resultant for Problem A and

ANSWERS Problem A § § R 2 = (5)2 + (10)2 R 2 =

Use Trigonometry to find the Direction (angle) of the Resultant § The direction of

Using the previous hiker problem, find the direction (angle) of the resultant § 1

§ The Calculated Angle is Not Always the Direction The measure of an angle

Your Turn!! Find theta for the resultant

ANSWERS Problem A Problem B § tan(Theta) = (5/10) = 0. 5 § Theta

Slides: 11

Download presentation

Finding the Magnitude and Direction of the Resultant for two vectors that form right angles to each other.

Find the Magnitude Using the Pythagorean Theorem § The Pythagorean theorem is a useful method for determining the result of adding two (and only two) vectors that make a right angle to each other. § The Pythagorean theorem is a mathematical equation that allows you to find the magnitude of the resultant.

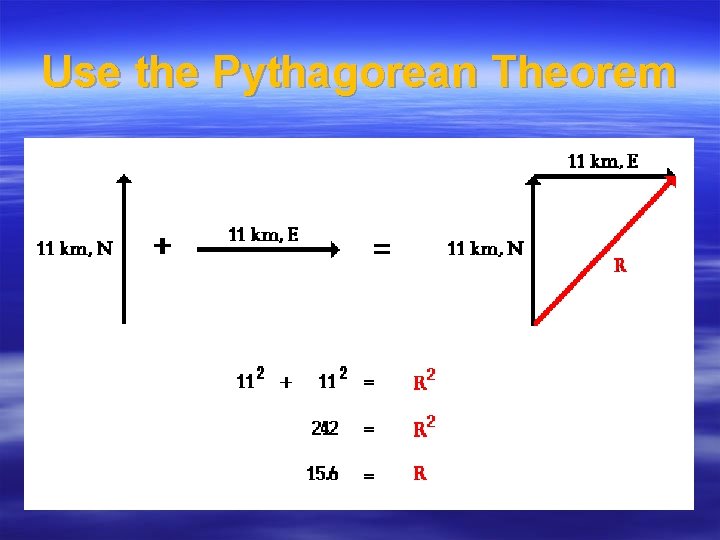
Example Problem § Eric leaves the base camp and hikes 11 km, north and then hikes 11 km east. Determine Eric's resulting displacement.

Use the Pythagorean Theorem

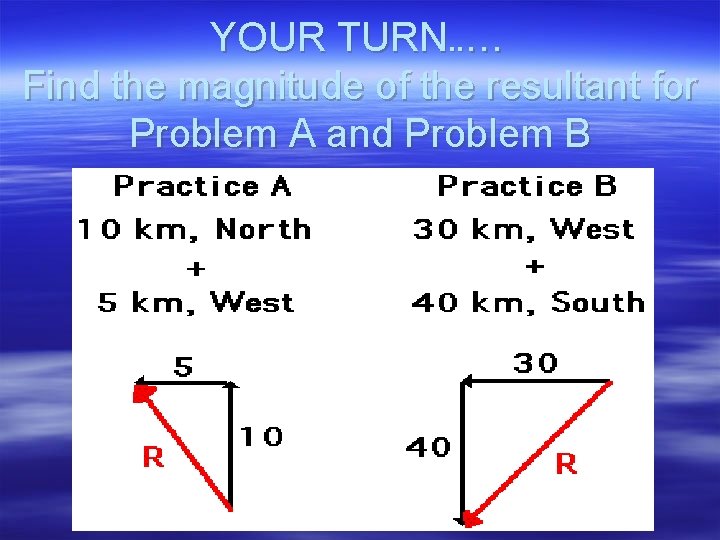
YOUR TURN. . … Find the magnitude of the resultant for Problem A and Problem B

ANSWERS Problem A § § R 2 = (5)2 + (10)2 R 2 = 125 R = SQRT (125( R = 11. 2 km Problem B § § R 2 = (30)2 + (40)2 R 2 = 2500 R = SQRT (2500( R = 50 km

Use Trigonometry to find the Direction (angle) of the Resultant § The direction of a resultant vector can often be determined by use of trigonometric functions. § SOH CAH TOA is a mnemonic that helps one remember the meaning of the three common trigonometric functions - sine, cosine, and tangent functions. § Once you have found the magnitude, you can use trig to find the direction (angle) of your resultant.

Using the previous hiker problem, find the direction (angle) of the resultant § 1 st Step: Identify theta (angle of the resultant) § **Theta is always measured at the tail end of your resultant.

§ The Calculated Angle is Not Always the Direction The measure of an angle as determined through use of SOH CAH TOA is not always the direction of the vector. The following vector addition diagram is an example of such a situation. Observe that the angle within the triangle is determined to be 26. 6 degrees using SOH CAH TOA. This angle does not include the horizon to 180 d degrees. § You must add 180 degrees to theta.

Your Turn!! Find theta for the resultant

ANSWERS Problem A Problem B § tan(Theta) = (5/10) = 0. 5 § Theta = tan-1 (0. 5) § Theta = 26. 6 degrees § Direction of R = 90 deg + 26. 6 deg § Direction of R = 116. 6 deg § tan(Theta) = (40/30) = 1. 333 § Theta = tan-1 (1. 333) § Theta = 53. 1 degrees § Direction of R = 180 deg + 53. 1 deg § Direction of R = 233. 1 deg