Finding roots of equations using the Newton Raphson




















- Slides: 28

Finding roots of equations using the Newton. Raphson method

Home Learning Objectives Introduction Petroleum Exercise: Preliminaries Petroleum Exercise Useful info Petroleum Exercise: Resources Preliminaries Petroleum Exercise HOME Quiz Useful Info Resources Quiz Info FAQ References Summary

Learning Objectives Introduction Petroleum Exercise: Preliminaries Learning objectives in this module 1. Petroleum Exercise Useful info Resources Quiz 2. 3. Develop problem solution skills using computers and numerical methods Review of the Newton-Raphson method Develop programming skills using FORTRAN elements in this module input/output loops format Info FAQ References Summary

Introduction Learning Objectives Introduction Petroleum Exercise: Preliminaries Petroleum Exercise Ø Finding roots of equations is one of the oldest applications of mathematics, and is required for a large variety of applications, also in the petroleum area. A familiar equation is the simple quadratic equation (1) Useful info Resources Quiz where the roots of the equation are given by (2) Ø These two roots to the quadratic equation are simply the values of x for which the equation is satisfied, i. e. the left side of eq. (1) is zero. Ø How would you do this in Fortran? Think it through and see this Example of how it could be done More Info FAQ References Summary

Introduction Learning Objectives Introduction Ø In a more general form, we are given a function of x, F(x), and we wish to find a value for x for which: Ø The function F(x) may be algebraic or transcendental, and we generally assume that it may be differentiated. Ø In practice, the functions we deal with in petroleum applications have no simple closed formula for their roots, as the quadratic equation above has. Instead, we turn to methods for approximation of the roots, and two steps are involved: Petroleum Exercise: Preliminaries Petroleum Exercise Useful info Resources Quiz 1 2 Ø Finding an approximate root Refining the approximation to wanted accuracy The first step will normally be a qualified guess based on the physics of the system. For the second step, a variety of methods exists. Please see the textbook for a discussion of various methods. More Info FAQ References Summary

Introduction Learning Objectives Introduction Petroleum Exercise: Preliminaries Petroleum Exercise Ø Here, we will concern ourselves with the Newton-Raphson method. For the derivation of the formula used for solving a one-dimensional problem, we simply make a first-order Taylor series expansion of the function F(x) Useful info Resources (4) Let us use the following notation for the x-values: Quiz (5) Then, eq. (4) may be rewritten as (6) More Info FAQ References Summary

Introduction Learning Objectives Introduction Ø Setting Eq. (6) to zero and solving for xk+1 yields the following expression Petroleum Exercise: Preliminaries (7) Petroleum Exercise Useful info Resources Quiz Ø This is the one-dimensional Newton-Raphson iterative equation, where represents the refined approximation at iteration level k+1, and is the approximation at the previous iteration level ( k). View Graphic Illustration Info FAQ References Summary

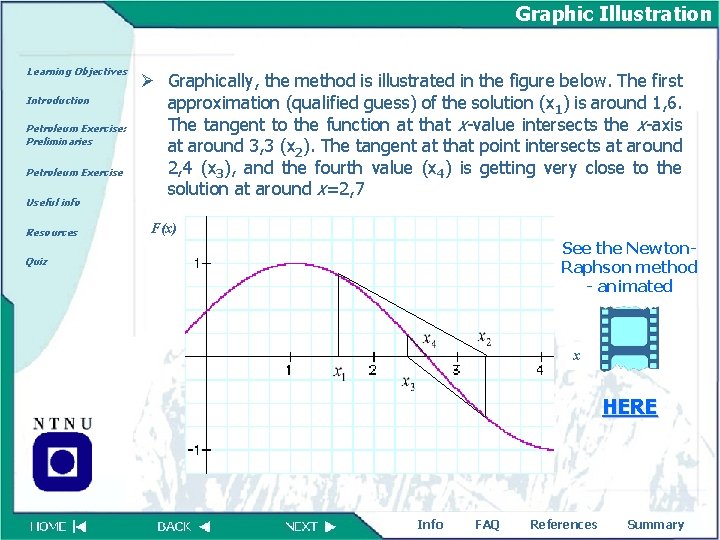
Graphic Illustration Learning Objectives Introduction Petroleum Exercise: Preliminaries Petroleum Exercise Useful info Resources Ø Graphically, the method is illustrated in the figure below. The first approximation (qualified guess) of the solution (x 1) is around 1, 6. The tangent to the function at that x-value intersects the x-axis at around 3, 3 (x 2). The tangent at that point intersects at around 2, 4 (x 3), and the fourth value (x 4) is getting very close to the solution at around x=2, 7 F(x) See the Newton. Raphson method - animated Quiz x HERE Info FAQ References Summary

Petroleum Exercise: Preliminaries Learning Objectives Introduction Petroleum Exercise: Preliminaries Equations of State (EOS) are used for description of PVT-behavior (Pressure-Volume-Temperature) of hydrocarbon gases. One such equation is the Beattie-Bridgeman equation: Petroleum Exercise Useful info Resources (8) Quiz P is pressure in atmospheres (atm) V is molar volume (liter/g mole) T is temperature (o. K) R is the universal gas constant (0, 08205 liter-atm / o. K-g mole) Next Info FAQ References Summary

Beta Learning Objectives Introduction Petroleum Exercise: Preliminaries Equations of State (EOS) are used for description of PVT-behavior (Pressure-Volume-Temperature) of hydrocarbon gases. One such equation is the Beattie-Bridgeman equation: Petroleum Exercise Useful info Resources (8) Quiz P is pressure in atmospheres (atm) V is molar volume (l/g mole) T is temperature (o. K) R is the universal gas constant (0, 08205 liter-atm / o. K-g mole) A 0, B 0, a, b, c are gas specific constants Next Info FAQ References Summary

Gamma Learning Objectives Introduction Petroleum Exercise: Preliminaries Equations of State (EOS) are used for description of PVT-behavior (Pressure-Volume-Temperature) of hydrocarbon gases. One such equation is the Beattie-Bridgeman equation: Petroleum Exercise Useful info Resources (8) Quiz P is pressure in atmospheres (atm) V is molar volume (l/g mole) T is temperature (o. K) R is the universal gas constant (0, 08205 liter-atm / o. K-g mole) A 0, B 0, a, b, c are gas specific constants Next Info FAQ References Summary

Delta Learning Objectives Introduction Petroleum Exercise: Preliminaries Equations of State (EOS) are used for description of PVT-behavior (Pressure-Volume-Temperature) of hydrocarbon gases. One such equation is the Beattie-Bridgeman equation: Petroleum Exercise Useful info Resources (8) Quiz P is pressure in atmospheres (atm) V is molar volume (l/g mole) T is temperature (o. K) R is the universal gas constant (0, 08205 liter-atm / o. K-g mole) A 0, B 0, a, b, c are gas specific constants Next Info FAQ References Summary

Petroleum Exercise: Preliminaries Learning Objectives Introduction Petroleum Exercise: Preliminaries After solving for the root of the eq. (8), ie. for the value for V that satisfies the equation for one particular set of pressure and temperature, we may find the corresponding compressibility factor (Z-factor) for the gas using the formula (the gas law for a real gas): Petroleum Exercise Useful info Resources Quiz PV = ZRT (12) Which can be rearranged to. . . Z= PV RT (obviously) Next Info FAQ References Summary

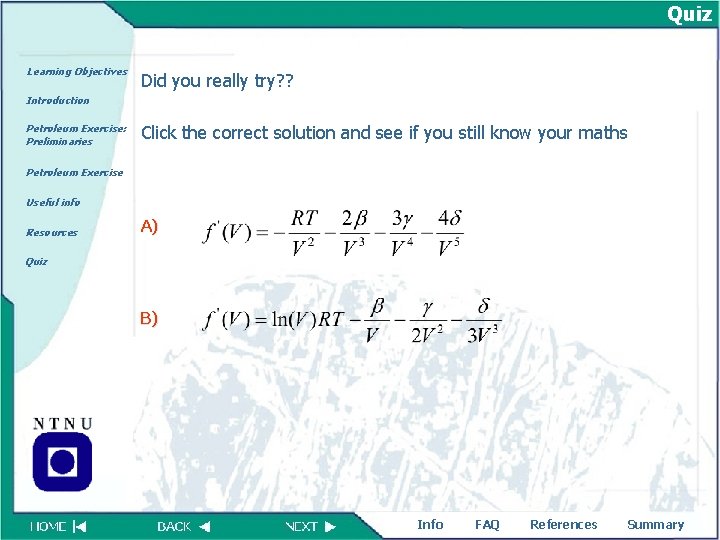
Petroleum Exercise: Preliminaries Learning Objectives Introduction The procedure for the exercise is described in the following. First, we rewrite the Beattie-Bridgeman equation as: Petroleum Exercise: Preliminaries (13) Petroleum Exercise Useful info Resources Quiz Then, we take the derivative of the function F(V) at constant P and T Try yourself! What is the derivative of F (V)? then check the Info Answer (click) FAQ References Summary

Quiz Learning Objectives Did you really try? ? Introduction Petroleum Exercise: Preliminaries Click the correct solution and see if you still know your maths Petroleum Exercise Useful info Resources A) Quiz B) Info FAQ References Summary

Right Answer Learning Objectives Introduction Petroleum Exercise: Preliminaries Right Answer!! Petroleum Exercise Useful info Resources Quiz BACK Info FAQ References Summary

Wrong Answer Learning Objectives Introduction Petroleum Exercise: Preliminaries Sorry, Wrong Answer!! Petroleum Exercise Useful info Resources Quiz BACK Info FAQ References Summary

Petroleum Exercise: Preliminaries Learning Objectives Now, the derivate of the function F(V) at constant P & T being Introduction Petroleum Exercise: Preliminaries (14) Petroleum Exercise Useful info Resources using the Newton-Raphson formula of eq. (7), we may find the root of Eq. (13) iteratively Quiz and after reducing the fraction, we get where k is the iteration counter More Info FAQ References Summary

Petroleum Exercise: Preliminaries Learning Objectives Introduction Petroleum Exercise: Preliminaries For the first iteration (k=1) we need a start value V 1. Here, we estimate a value using the ideal gas law (assuming Z=1): Petroleum Exercise Useful info Resources PV=RT or V 1=RT / P Quiz The iterative procedure is terminated when the relative change in V is less than a prescribed convergence criterion, e, i. e. Info FAQ References Summary

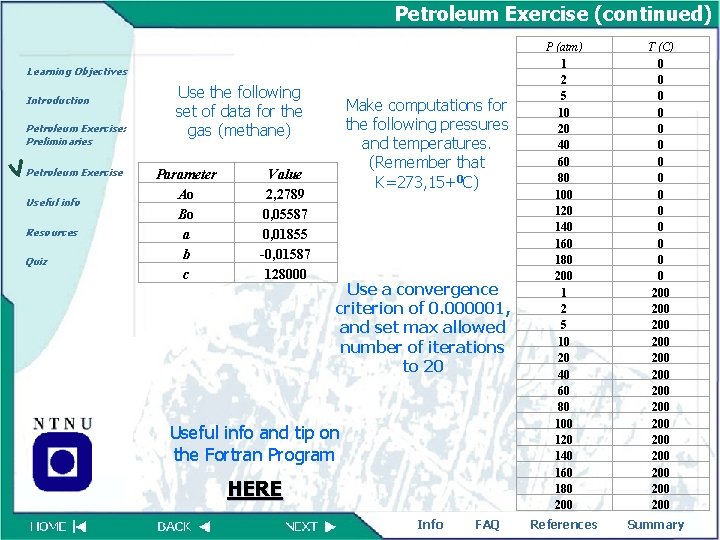
Petroleum Exercise Learning Objectives Tasks to be completed Introduction Petroleum Exercise: Preliminaries Petroleum Exercise Useful info Resources Quiz 1 Make a FORTRAN program that uses the Newton-Raphson method to solve the Beattie-Bridgeman equation for molar volume (V ) for any gas (i. e. . for any set of the parameters A 0, B 0, a, b, c) at a given pressure (P ) and a given temperature (T ). After finding the volume (V ), the compressibility factor (Z ) should be computed. The computer program will read all parameters, and pressure and temperature, from the input file, and should write the computed parameters, pressure and temperature, and computed compressibility factor, for each set of pressure and temperature to the output file. 2 Run the computer program for This data set 3 Make a plot of compressibility factor vs. pressure for the two different temperatures (on the same figure). Info FAQ References Summary

Petroleum Exercise (continued) Learning Objectives Introduction Petroleum Exercise: Preliminaries Petroleum Exercise Useful info Resources Quiz Use the following set of data for the gas (methane) Parameter Ao Bo a b c Value 2, 2789 0, 05587 0, 01855 -0, 01587 128000 Make computations for the following pressures and temperatures. (Remember that K=273, 15+0 C) Use a convergence criterion of 0. 000001, and set max allowed number of iterations to 20 Useful info and tip on the Fortran Program HERE Info FAQ P (atm) 1 2 5 10 20 40 60 80 100 120 140 160 180 200 References T (C) 0 0 0 0 200 200 200 200 Summary

Useful Info Learning Objectives Introduction Petroleum Exercise: Preliminaries Petroleum Exercise Useful info For the Newton-Raphson program Ø Ø Include an input and an output file. For the iterative operation, the DO loop is recommended. The convergence criterion should be tested with the IF statement Find a reasonable format in which to present your calculations Resources Quiz All clear? Go to Work!! Resources Info FAQ References Summary

Resources Learning Objectives Introduction to Fortran Introduction Petroleum Exercise: Preliminaries Petroleum Exercise Fortran Template here The whole exercise in a printable format here Useful info Resources Quiz Web sites Ø Numerical Recipes Ø Fortran Tutorial Ø Professional Programmer's Guide to Fortran 77 Ø Programming in Fortran 77 Info FAQ References Summary

Quiz Learning Objectives Introduction This section includes a quiz on the topics covered by this module. Petroleum Exercise: Preliminaries Petroleum Exercise Useful info The quiz is meant as a control to see if you have learned some of the most important features Resources Quiz Hit object to start quiz Info FAQ References Summary

General information Learning Objectives Introduction Petroleum Exercise: Preliminaries Petroleum Exercise Useful info Resources Quiz Title: Finding roots of equations using the Newton-Raphson method Teacher(s): Professor Jon Kleppe Assistant(s): Per Jørgen Dahl Svendsen Abstract: Provide a good background for solving problems within petroleum related topics using numerical methods 4 keywords: Newtons Method, Loops, Fortran, Input/Output Topic discipline: Level: 2 Prerequisites: None Learning goals: Develop problem solution skills using computers and numerical methods Size in megabytes: 0. 7 MB Software requirements: MS Power Point 2002 or later, Flash Player 6. 0 Estimated time to complete: Copyright information: The author has copyright to the module and use of the content must be in agreement with the responsible author or in agreement with http: //www. learningjournals. net. About the author Info FAQ References Summary

FAQ Learning Objectives Introduction Petroleum Exercise: Preliminaries Petroleum Exercise Useful info No questions have been posted yet. However, when questions are asked they will be posted here. Remember, if something is unclear to you, it is a good chance that there are more people that have the same question For more general questions and definitions try these Resources Quiz Dataleksikon Webopedia Schlumberger Oilfield Glossary Info FAQ References Summary

References Learning Objectives Introduction Petroleum Exercise: Preliminaries W. H. Preuss, et al. , “Numerical Recipes in Fortran”, 2 nd edition Cambridge University Press, 1992 Petroleum Exercise Useful info Resources Quiz Ø References to the textbook : Newton-Raphson Method Using Derivative: page 355 Ø The Textbook can also be accessed online: Numerical Recipes in Fortran Info FAQ References Summary

Summary Learning Objectives Introduction Subsequent to this module you should. . . Petroleum Exercise: Preliminaries Ø Petroleum Exercise Ø Useful info Ø Resources Ø be able to translate a problem to Fortran code write and handle DO loops have a feel for the output format know the conditional statements and use the IF structure Quiz Info FAQ References Summary