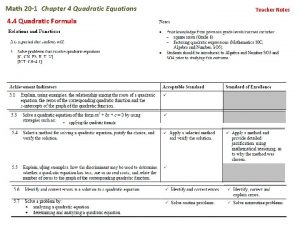
Finding Real Roots of of Finding Real Roots

Finding Real Roots of of Finding Real Roots 3 -5 Polynomial Equations Warm Up Lesson Presentation Lesson Quiz Holt Mc. Dougal Algebra 2 Algebra 22 Holt Mc. Dougal

3 -5 Finding Real Roots of Polynomial Equations Warm Up Factor completely. 1. 2 y 3 + 4 y 2 – 30 y 2 y(y – 3)(y + 5) 2. 3 x 4 – 6 x 2 – 24 3(x – 2)(x + 2)(x 2 + 2) Solve each equation. 3. x 2 – 9 = 0 x = – 3, 3 4. x 3 + 3 x 2 – 4 x = 0 Holt Mc. Dougal Algebra 2 x = – 4, 0, 1

3 -5 Finding Real Roots of Polynomial Equations Essential Question How can you find all the possible real zeros of f(x)? Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations Vocabulary multiplicity Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations In Lesson 3 -4, you used several methods for factoring polynomials. As with some quadratic equations, factoring a polynomial equation is one way to find its real roots. Recall the Zero Product Property from Lesson 2 -3. You can find the roots, or solutions, of the polynomial equation P(x) = 0 by setting each factor equal to 0 and solving for x. Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations Check It Out! Example 1 b Solve the polynomial equation by factoring. x 3 – 2 x 2 – 25 x = – 50 x 3 – 2 x 2 – 25 x + 50 = 0 Set the equation equal to 0. (x + 5)(x – 2)(x – 5) = 0 Factor. x + 5 = 0, x – 2 = 0, or x – 5 = 0 x = – 5, x = 2, or x = 5 Solve for x. The roots are – 5, 2, and 5. Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations Example 1 A: Using Factoring to Solve Polynomial Equations Solve the polynomial equation by factoring. 4 x 6 + 4 x 5 – 24 x 4 = 0 4 x 4(x 2 + x – 6) = 0 Factor out the GCF, 4 x 4(x + 3)(x – 2) = 0 Factor the quadratic. 4 x 4 = 0 or (x + 3) = 0 or (x – 2) = 0 Set each factor equal to 0. x = 0, x = – 3, x = 2 Solve for x. The roots are 0, – 3, and 2 where 0 has a multiplicity of 4. The number of roots equals the degree of the polynomial. Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations Example 1 A Continued Check Use a graph. The roots appear to be located at x = 0, x = – 3, and x = 2. Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations Solving Equations Using Quadratic Techniques An expression that is quadratic in form can be written as au² + bu + c for any numbers a, b, and c, a≠ 0, where u is some expression in x. The expression au² + bu + c is called the quadratic form of the original expression. This method of substituting u for x² is called u substitution. For example, let u = x² the expression x⁴ + 13 x² + 36 can be written as (x²)² + 13(x²) + 36 or u² +13 u + 36. Now you can easily factor into (u+9)(u+4). Substitute u = x² to get (x²+9)(x²+4). Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations Example 1 B: Using Factoring to Solve Polynomial Equations Solve the polynomial equation by factoring. x 4 + 25 = 26 x 2 x 4 – 26 x 2 + 25 = 0 Set the equation equal to 0. (x²)² = x⁴ (x²)² - 26(x²) + 25=0 Factor the trinomial in (x 2 – 25)(x 2 – 1) = 0 quadratic form. (x – 5)(x + 5)(x – 1)(x + 1) Factor the difference of two squares. x – 5 = 0, x + 5 = 0, x – 1 = 0, or x + 1 =0 x = 5, x = – 5, x = 1 or x = – 1 The roots are 5, – 5, 1, and – 1. Holt Mc. Dougal Algebra 2 Solve for x.

3 -5 Finding Real Roots of Polynomial Equations Sometimes a polynomial equation has a factor that appears more than once. This creates a multiple root. In 4 x 6 + 4 x 5 – 24 x 4 = 0, the polynomial has a multiple roots, 0, – 3, and 2. For example, the root 0 is a factor four times because 4 x 4 = 0. The multiplicity of root r is the number of times that x – r is a factor of P(x). When a real root has even multiplicity, the graph of y = P(x) touches the x-axis but does not cross it. When a real root has odd multiplicity greater than 1, the graph “bends” as it crosses the x-axis. Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations For example: You cannot always determine the multiplicity of a root from a graph. It is easiest to determine multiplicity when the polynomial is in factored form. Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations Example 2 A: Identifying Multiplicity Identify the roots of each equation. State the multiplicity of each root. x 3 + 6 x 2 + 12 x + 8 = 0 x 3 + 6 x 2 + 12 x + 8 = (x + 2)(x + 2) x + 2 is a factor three times. The root – 2 has a multiplicity of 3. Check Use a graph. A calculator graph shows a bend near (– 2, 0). Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations Example 2 B: Identifying Multiplicity Identify the roots of each equation. State the multiplicity of each root. x 4 + 8 x 3 + 18 x 2 – 27 = 0 x 4 + 8 x 3 + 18 x 2 – 27 = (x – 1)(x + 3)(x + 3) x – 1 is a factor once, and x + 3 is a factor three times. The root 1 has a multiplicity of 1. The root – 3 has a multiplicity of 3. Check Use a graph. A calculator graph shows a bend near (– 3, 0) and crosses at (1, 0). Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations Not all polynomials are factorable, but the Rational Root Theorem can help you find all possible rational roots of a polynomial equation. Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations Step 1 x 3 + 3 x 2 – 4 x – 12 = 0 Set the equation equal to 0. Step 2 Use the Rational Root Theorem to identify all possible rational roots. Factors of – 12: ± 1, ± 2, ± 3, ± 4, ± 6, ± 12 Step 3 Test the possible roots to find one that is actually a root. Use a synthetic substitution table to organize your work. The first row represents the coefficients of the polynomial. The first column represents the possible roots and the last column represents the remainders. Test possibilities to identify at least one root. Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations Example 3 Continued Step 4 Factor the polynomial. The synthetic substitution of 2 results in a remainder of 0, so 2 is a root and the polynomial in factored form is (x – 2)(x 2 + 5 x + 6) = 0 Set the equation equal to 0. (x – 2)(x + 3) = 0 Factor x 2 + 5 x + 6. x = 2, x = – 2, or x = – 3 Set each factor equal to 0, and solve. Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations Polynomial equations may also have irrational roots. Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations The Irrational Root Theorem say that irrational roots come in conjugate pairs. For example, if you know that 1 + is a root of x 3 – x 2 – 3 x – 1 = 0, then you know that 1 – is also a root. Recall that the real numbers are made up of the rational and irrational numbers. You can use the Rational Root Theorem and the Irrational Root Theorem together to find all of the real roots of P(x) = 0. Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations Example 4: Identifying All of the Real Roots of a Polynomial Equation Identify all the real roots of 2 x 3 – 9 x 2 + 2 = 0. Step 1 Use the Rational Root Theorem to identify possible rational roots. ± 1, ± 2 = ± 1, ± 2, ± 1. p = 2 and q = 2 ± 1, ± 2 2 Step 2 Graph y = 2 x 3 – 9 x 2 + 2 to find the x-intercepts. The x-intercepts are located at or near – 0. 45, 0. 5, and 4. 45. The x-intercepts – 0. 45 and 4. 45 do not correspond to any of the possible rational roots. Holt Mc. Dougal Algebra 2

Finding Real Roots of Polynomial Equations 3 -5 Example 4 Continued Step 3 Test the possible rational root 1 2 2 – 9 0 2 1 – 4 – 2 2 – 8 – 4 0 1. 2 1. The remainder is 2 1 0, so (x – ) is a factor. 2 Test 1 The polynomial factors into (x – )(2 x 2 – 8 x – 4). 2 Step 4 Solve 2 x 2 – 8 x – 4 = 0 to find the remaining roots. 2(x 2 – 4 x – 2) = 0 Factor out the GCF, 2 Use the quadratic formula to 4± 16+8 =2 ± 6 x= identify the irrational roots. 2 Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations Example 4 Continued The fully factored equation is ( ) ( æ 1öé 2 ç x – ÷ ë x – 2 + 6 ùû éëx – 2ø è ) 6 ùû = 0 1 The roots are , 2 + 6 , and 2 - 6. 2 Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations Check It Out! Example 4 Identify all the real roots of 2 x 3 – 3 x 2 – 10 x – 4 = 0. Step 1 Use the Rational Root Theorem to identify possible rational roots. ± 1, ± 2, ± 4 = ± 1, ± 2, ± 4, ± 1, ± 2 2 p = – 4 and q = 2 Step 2 Graph y = 2 x 3 – 3 x 2 – 10 x – 4 to find the xintercepts. The x-intercepts are located at or near – 0. 5, – 1. 2, and 3. 2. The x-intercepts – 1. 2 and 3. 2 do not correspond to any of the possible rational roots. Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations Check It Out! Example 4 Continued 1 Step 3 Test the possible rational root –. 2 1 1 Test –. The remainder 2 – 3 – 10 – 4 – 2 2 1 is 0, so (x + ) is a factor. – 1 2 4 2 2 – 4 – 8 0 1 The polynomial factors into (x + )(2 x 2 – 4 x – 8). 2 Step 4 Solve 2 x 2 – 4 x – 8 = 0 to find the remaining roots. 2(x 2 – 2 x – 4) = 0 Factor out the GCF, 2 Use the quadratic formula to 2± 4+16 x= =1± 5 identify the irrational roots. 2 Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations Check It Out! Example 4 Continued The fully factored equation is æ 1ö 2 çx + ÷ éx – 2ø ë è ( 1+ 5 )ùû éë x – (1– 5)ùû 1 The roots are – , 1 + 5 , and 1 - 5. 2 Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations Lesson Quiz Solve by factoring. 1. x 3 + 9 = x 2 + 9 x – 3, 3, 1 Identify the roots of each equation. State the multiplicity of each root. 0 and 2 each with 2. 5 x 4 – 20 x 3 + 20 x 2 = 0 multiplicity 2 3. x 3 – 12 x 2 + 48 x – 64 = 0 4 with multiplicity 3 4. A box is 2 inches longer than its height. The width is 2 inches less than the height. The volume of the box is 15 cubic inches. How tall is the box? 3 in. 5. Identify all the real roots of x 3 + 5 x 2 – 3 x – 3 = 0. 1, -3 + 6, -3 - 6 Holt Mc. Dougal Algebra 2

3 -5 Finding Real Roots of Polynomial Equations Why is the Rational Root Theorem so polite? It minds its p’s and q’s! Holt Mc. Dougal Algebra 2