FINDING MULTIPLE ROOTS OF NONLINEAR EQUATION USING VARIETY

FINDING MULTIPLE ROOTS OF NONLINEAR EQUATION USING VARIETY OF TWO-STEP METHOD NAME: NIK NUR LAILI NAZIFA BINTI MOHD ROZI STUDENT ID: 2017696334 SUPERVISOR: DR. RIVAIE BIN MOHD ALI

INTRODUCTION • Numerical analysis is a field of mathematics and computer science that creates, analyzes and implements algorithms to obtain numerical solutions to continuous variables problem (Atkinson, K. , 2017). • It is very important in numerical analysis to find the origin of nonlinear equations and has many applications in engineering and other applied sciences. • In 1685, John Wallis published the first scheme for the discovery of the roots of nonlinear equations. Its simplified description was published by Joseph Raphson in 1690 and was called the Newton. Raphson method. • Given the disadvantages of Newton's method, several multipoint approaches for discovering simple root nonlinear equations have been established in the recent past utilizing Newton’s method as a first step (Zafar, F. et al. , 2015).

PROBLEM STATEMENTS • Method such as Bisection, Newton and Secant method are commonly used to find root govern by the formula f(a). f(b) < 0. • The first problem is numerical method fail to distinguish multiple. • The second problem is the existing methods cannot be applied to find the multiple roots. • To find the accuracy of the proposed methods and slow CPU time.

OBJECTIVES • To find the multiple root of a nonlinear function using four different numerical methods. • To analyze the efficiency of these numerical methods based on number of iteration and CPU time. • To determine the best numerical method for finding multiple root of nonlinear function.

LITERATURE REVIEW • Halley’s method: • Schroder’s method:

• Li et al (2009) method: • Dong’s method:

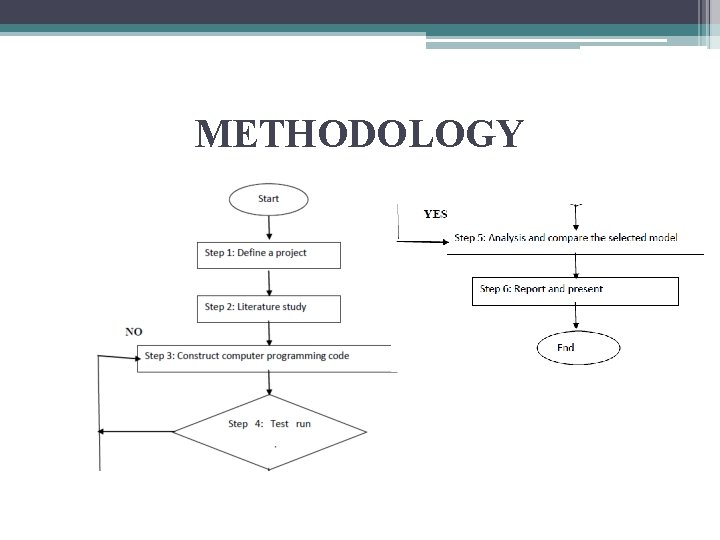
METHODOLOGY

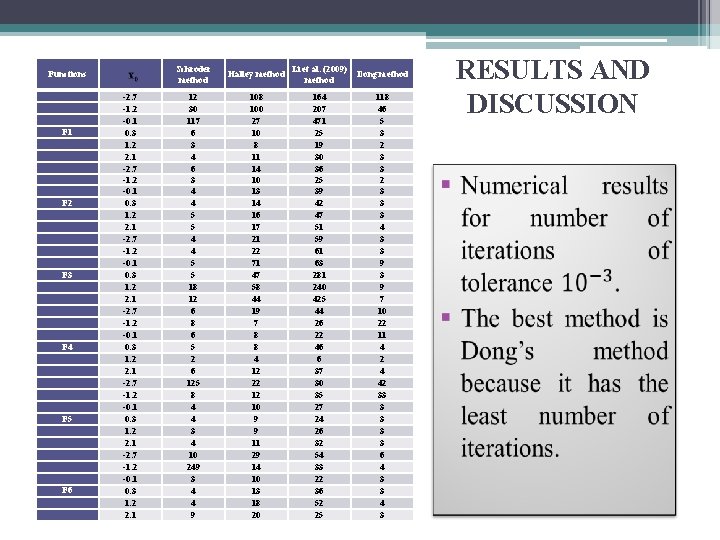
Functions F 1 F 2 F 3 F 4 F 5 F 6 -2. 7 -1. 2 -0. 1 0. 3 1. 2 2. 1 Schroder method Halley method Li et al. (2009) method Dong method 12 30 117 6 3 4 4 5 5 18 12 6 8 6 5 2 6 125 8 4 4 3 4 10 249 3 4 4 9 108 100 27 10 8 11 14 10 13 14 16 17 21 22 71 47 58 44 19 7 8 8 4 12 22 12 10 9 9 11 29 14 10 13 18 20 164 207 471 25 19 30 36 25 39 42 47 51 59 61 63 281 240 425 44 26 22 46 6 37 30 35 27 24 26 32 54 33 22 36 52 25 118 46 5 3 2 3 3 3 4 3 3 9 7 10 22 11 4 2 4 42 33 3 3 6 4 3 3 4 3 RESULTS AND DISCUSSION

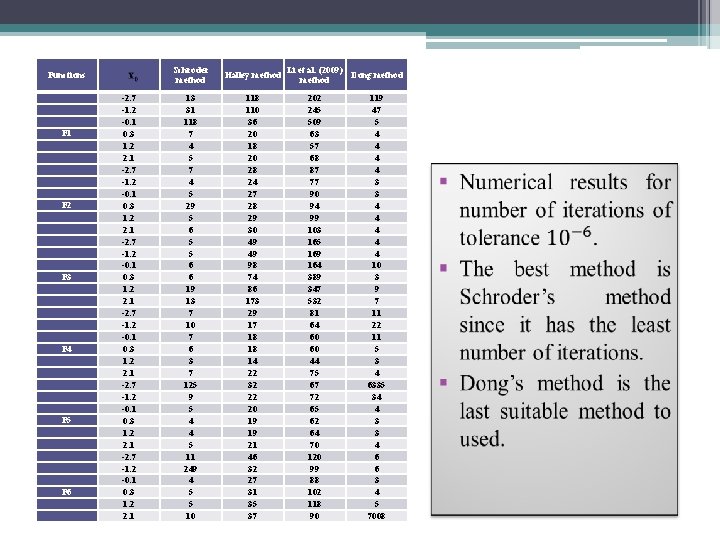
Functions F 1 F 2 F 3 F 4 F 5 F 6 -2. 7 -1. 2 -0. 1 0. 3 1. 2 2. 1 Schroder method Halley method 13 31 118 7 4 5 29 5 6 5 5 6 6 19 13 7 10 7 6 3 7 125 9 5 4 4 5 11 249 4 5 5 10 118 110 36 20 18 20 28 24 27 28 29 30 49 49 98 74 86 173 29 17 18 18 14 22 32 22 20 19 19 21 46 32 27 31 35 37 Li et al. (2009) Dong method 202 245 509 63 57 68 87 77 90 94 99 103 165 169 164 389 347 532 81 64 60 60 44 75 67 72 65 62 64 70 120 99 88 102 118 90 119 47 5 4 4 3 3 4 4 4 10 3 9 7 11 22 11 5 3 4 6335 34 4 3 3 4 6 6 3 4 5 7008

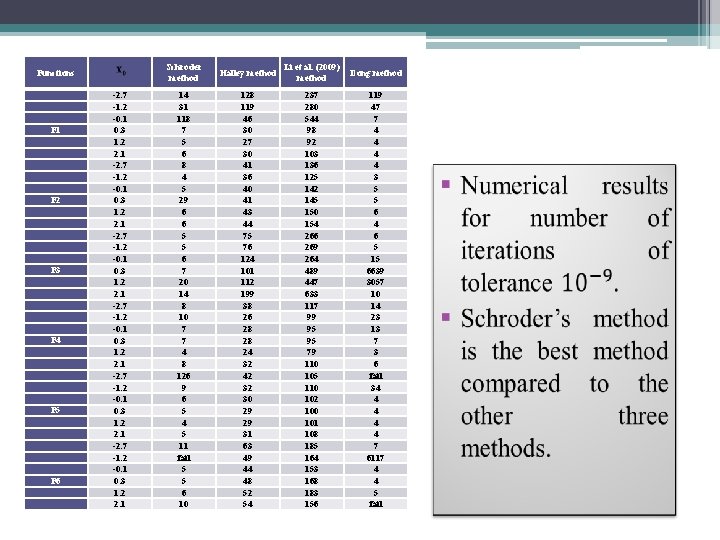
Functions F 1 F 2 F 3 F 4 F 5 F 6 -2. 7 -1. 2 -0. 1 0. 3 1. 2 2. 1 Schroder method Halley method Li et al. (2009) method Dong method 14 31 118 7 5 6 8 4 5 29 6 6 5 5 6 7 20 14 8 10 7 7 4 8 126 9 6 5 4 5 11 fail 5 5 6 10 128 119 46 30 27 30 41 36 40 41 43 44 75 76 124 101 112 199 38 26 28 28 24 32 42 32 30 29 29 31 63 49 44 48 52 54 237 280 544 98 92 103 136 125 142 145 150 154 266 269 264 489 447 633 117 99 95 95 79 110 105 110 102 100 101 108 185 164 153 168 183 156 119 47 7 4 4 3 5 5 6 4 6 5 15 6639 3057 10 14 23 13 7 3 6 fail 34 4 4 7 6117 4 4 5 fail

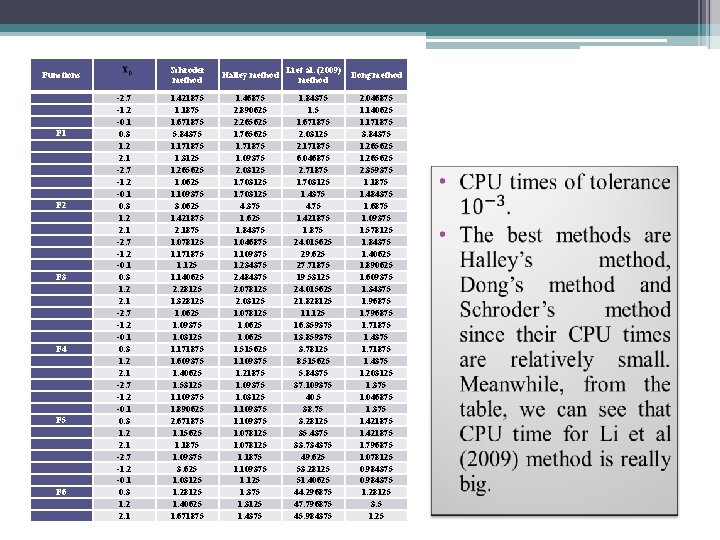
Functions F 1 F 2 F 3 F 4 F 5 F 6 -2. 7 -1. 2 -0. 1 0. 3 1. 2 2. 1 Schroder method Halley method Li et al. (2009) method Dong method 1. 421875 1. 671875 5. 84375 1. 171875 1. 3125 1. 265625 1. 0625 1. 109375 3. 0625 1. 421875 2. 1875 1. 078125 1. 171875 1. 125 1. 140625 2. 28125 1. 328125 1. 0625 1. 09375 1. 03125 1. 171875 1. 609375 1. 40625 1. 53125 1. 109375 1. 890625 2. 671875 1. 15625 1. 1875 1. 09375 3. 625 1. 03125 1. 28125 1. 40625 1. 671875 1. 46875 2. 890625 2. 265625 1. 71875 1. 09375 2. 03125 1. 703125 4. 375 1. 625 1. 84375 1. 046875 1. 109375 1. 234375 2. 484375 2. 078125 2. 03125 1. 078125 1. 0625 1. 515625 1. 109375 1. 21875 1. 09375 1. 03125 1. 109375 1. 078125 1. 1875 1. 109375 1. 125 1. 375 1. 3125 1. 4375 1. 84375 1. 671875 2. 03125 2. 171875 6. 046875 2. 71875 1. 703125 1. 4375 4. 75 1. 421875 1. 875 24. 015625 29. 625 27. 71875 19. 53125 24. 015625 21. 828125 11. 125 16. 359375 13. 859375 3. 78125 8. 515625 5. 84375 37. 109375 40. 5 38. 75 3. 28125 35. 4375 33. 734375 49. 625 53. 28125 51. 40625 44. 296875 47. 796875 45. 984375 2. 046875 1. 140625 1. 171875 3. 84375 1. 265625 2. 359375 1. 1875 1. 484375 1. 6875 1. 09375 1. 578125 1. 84375 1. 40625 1. 890625 1. 609375 1. 34375 1. 96875 1. 71875 1. 4375 1. 203125 1. 375 1. 046875 1. 375 1. 421875 1. 796875 1. 078125 0. 984375 1. 28125 3. 5 1. 25

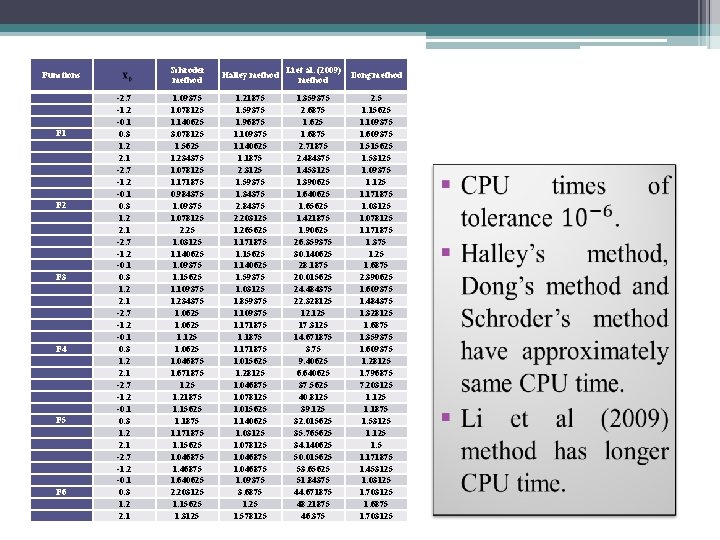
Functions F 1 F 2 F 3 F 4 F 5 F 6 -2. 7 -1. 2 -0. 1 0. 3 1. 2 2. 1 Schroder method Halley method Li et al. (2009) method Dong method 1. 09375 1. 078125 1. 140625 3. 078125 1. 5625 1. 234375 1. 078125 1. 171875 0. 984375 1. 09375 1. 078125 2. 25 1. 03125 1. 140625 1. 09375 1. 15625 1. 109375 1. 234375 1. 0625 1. 125 1. 0625 1. 046875 1. 671875 1. 21875 1. 15625 1. 1875 1. 171875 1. 15625 1. 046875 1. 640625 2. 203125 1. 15625 1. 3125 1. 21875 1. 59375 1. 96875 1. 109375 1. 140625 1. 1875 2. 3125 1. 59375 1. 34375 2. 84375 2. 203125 1. 265625 1. 171875 1. 15625 1. 140625 1. 59375 1. 03125 1. 859375 1. 109375 1. 171875 1. 015625 1. 28125 1. 046875 1. 078125 1. 015625 1. 140625 1. 03125 1. 078125 1. 046875 1. 09375 3. 6875 1. 25 1. 578125 1. 359375 2. 6875 1. 625 1. 6875 2. 71875 2. 484375 1. 453125 1. 390625 1. 640625 1. 65625 1. 421875 1. 90625 26. 359375 30. 140625 28. 1875 20. 015625 24. 484375 22. 328125 12. 125 17. 3125 14. 671875 3. 75 9. 40625 6. 640625 37. 5625 40. 8125 39. 125 32. 015625 35. 765625 34. 140625 50. 015625 53. 65625 51. 84375 44. 671875 48. 21875 46. 375 2. 5 1. 15625 1. 109375 1. 609375 1. 515625 1. 53125 1. 09375 1. 125 1. 171875 1. 03125 1. 078125 1. 171875 1. 375 1. 25 1. 6875 2. 390625 1. 609375 1. 484375 1. 328125 1. 6875 1. 359375 1. 609375 1. 28125 1. 796875 7. 203125 1. 1875 1. 53125 1. 171875 1. 453125 1. 03125 1. 703125 1. 6875 1. 703125

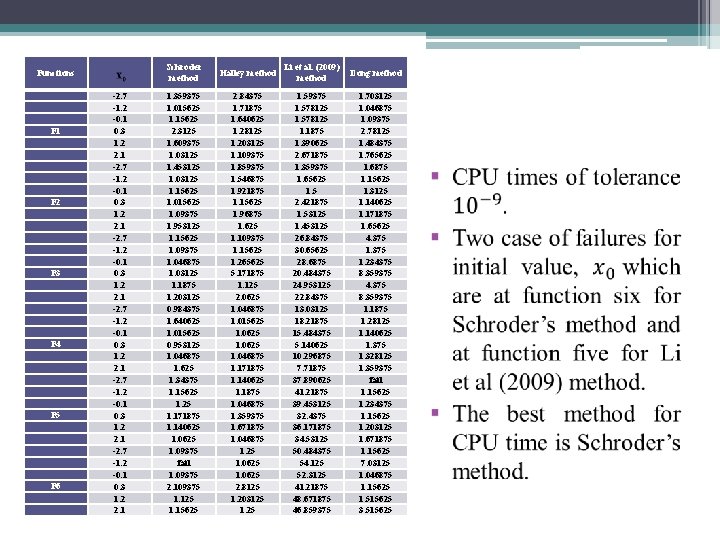
Functions F 1 F 2 F 3 F 4 F 5 F 6 -2. 7 -1. 2 -0. 1 0. 3 1. 2 2. 1 Schroder method Halley method Li et al. (2009) method Dong method 1. 359375 1. 015625 1. 15625 2. 3125 1. 609375 1. 03125 1. 453125 1. 03125 1. 15625 1. 09375 1. 953125 1. 15625 1. 09375 1. 046875 1. 03125 1. 1875 1. 203125 0. 984375 1. 640625 1. 015625 0. 953125 1. 046875 1. 625 1. 34375 1. 15625 1. 171875 1. 140625 1. 09375 fail 1. 09375 2. 109375 1. 125 1. 15625 2. 84375 1. 71875 1. 640625 1. 28125 1. 203125 1. 109375 1. 859375 1. 546875 1. 921875 1. 15625 1. 96875 1. 625 1. 109375 1. 15625 1. 265625 5. 171875 1. 125 2. 0625 1. 046875 1. 015625 1. 0625 1. 046875 1. 171875 1. 140625 1. 1875 1. 046875 1. 359375 1. 671875 1. 046875 1. 25 1. 0625 2. 8125 1. 203125 1. 59375 1. 578125 1. 1875 1. 390625 2. 671875 1. 359375 1. 65625 1. 5 2. 421875 1. 53125 1. 453125 26. 84375 30. 65625 28. 6875 20. 484375 24. 953125 22. 84375 13. 03125 18. 21875 15. 484375 5. 140625 10. 296875 7. 71875 37. 890625 41. 21875 39. 453125 32. 4375 36. 171875 34. 53125 50. 484375 54. 125 52. 3125 41. 21875 48. 671875 46. 859375 1. 703125 1. 046875 1. 09375 2. 78125 1. 484375 1. 765625 1. 6875 1. 15625 1. 3125 1. 140625 1. 171875 1. 65625 4. 375 1. 234375 8. 359375 4. 375 8. 359375 1. 1875 1. 28125 1. 140625 1. 375 1. 328125 1. 359375 fail 1. 15625 1. 234375 1. 15625 1. 203125 1. 671875 1. 15625 7. 03125 1. 046875 1. 15625 1. 515625 3. 515625

CONCLUSION AND RECOMMENDATION • Halley’s method is the best approach when resolving these functions. • In terms of CPU time, the result show that even though Schroder’s method. • Test function has been applied with larger intervals. • Try on more different functions try on more different functions.

THANK YOU