FINDING LIMITS GRAPHICALLY AND NUMERICALLY Section 1 2





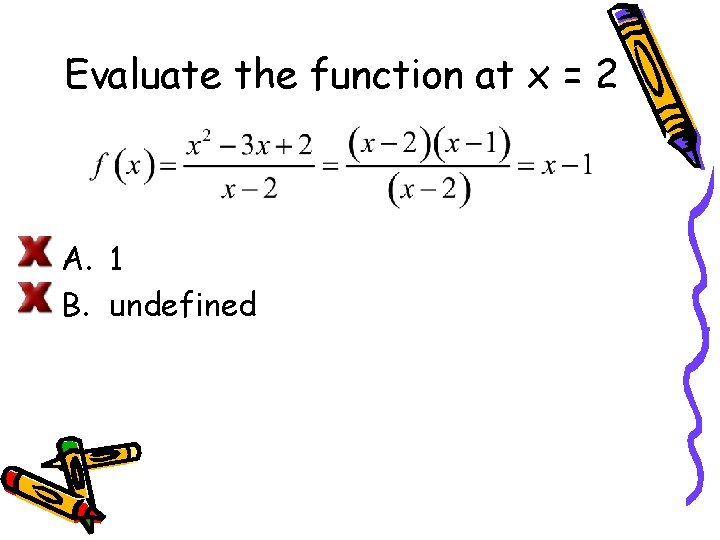


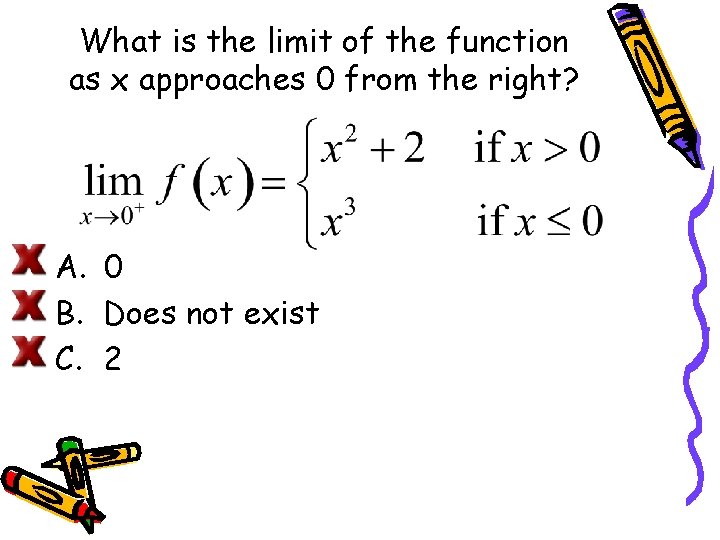
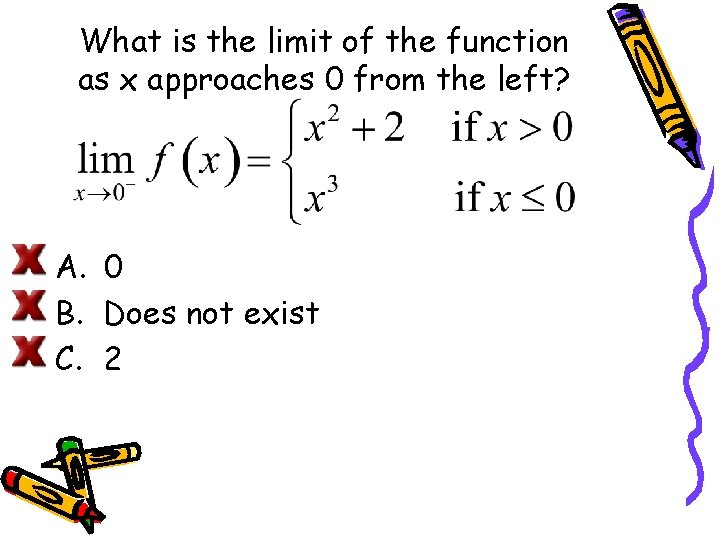
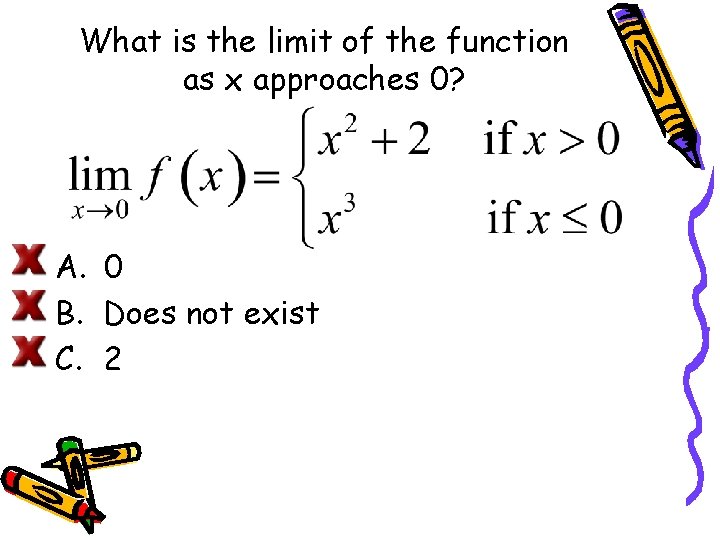




- Slides: 17

FINDING LIMITS GRAPHICALLY AND NUMERICALLY Section 1. 2

When you are done with your homework, you should be able to… – Estimate a limit using a numerical or graphic approach – Learn different ways that a limit can fail to exist – Study and use a formal definition of limit

AN INTRODUCTION TO LIMITS Consider the function

What is the domain? A. B. C. D. E. Both C and D

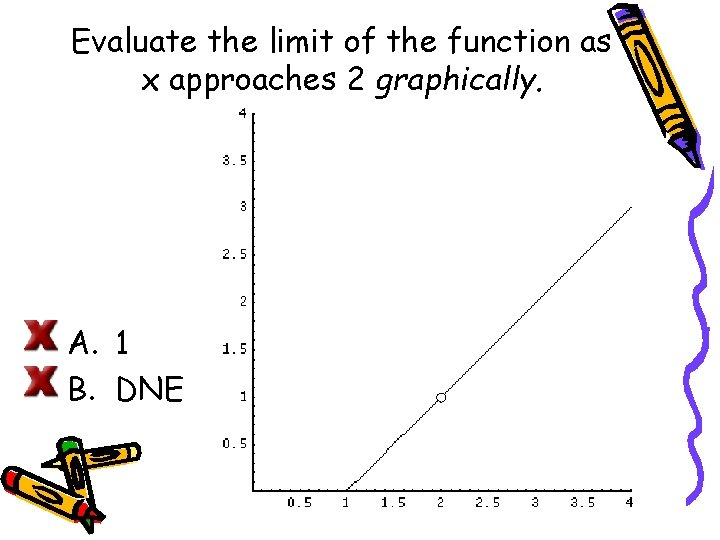
Consider the limit of this function as x approaches 2. When graphing the function, we could factor the numerator and cancel, keeping in mind there will be a break in the graph at. So we have which is the graph of a line with an open circle at Let’s first estimate the limit as x approaches 2 graphically. Or, writing this mathematically, .
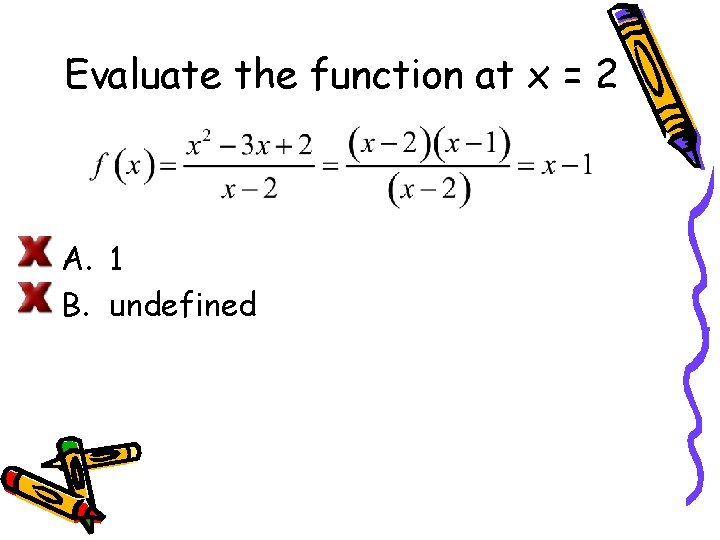
Evaluate the function at x = 2 A. 1 B. undefined

Evaluate the limit of the function as x approaches 2 graphically. A. 1 B. DNE

Now, let’s estimate numerically using a table of values. 1. 75 1. 999 2 2. 001 2. 25 0. 75 0. 999 ? 1. 001 1. 25 Since is approaching 1 from the left and right of 2, we may conclude that

LIMITS THAT FAIL TO EXIST Behavior that differs from the right to the left. Consider
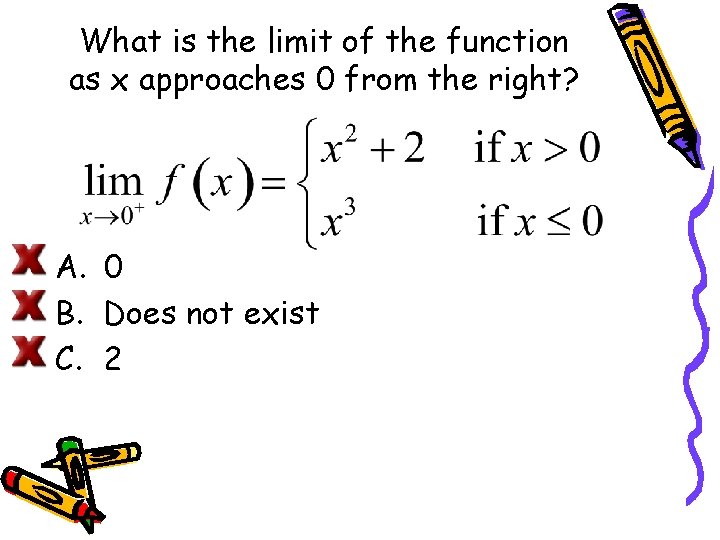
What is the limit of the function as x approaches 0 from the right? A. 0 B. Does not exist C. 2
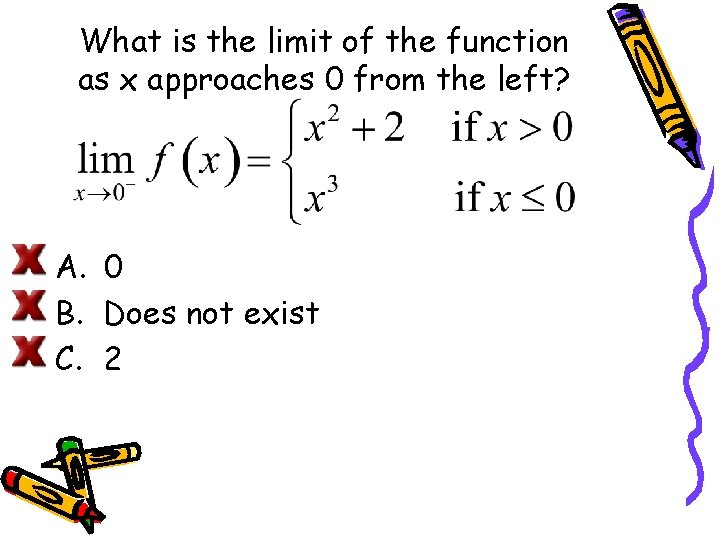
What is the limit of the function as x approaches 0 from the left? A. 0 B. Does not exist C. 2
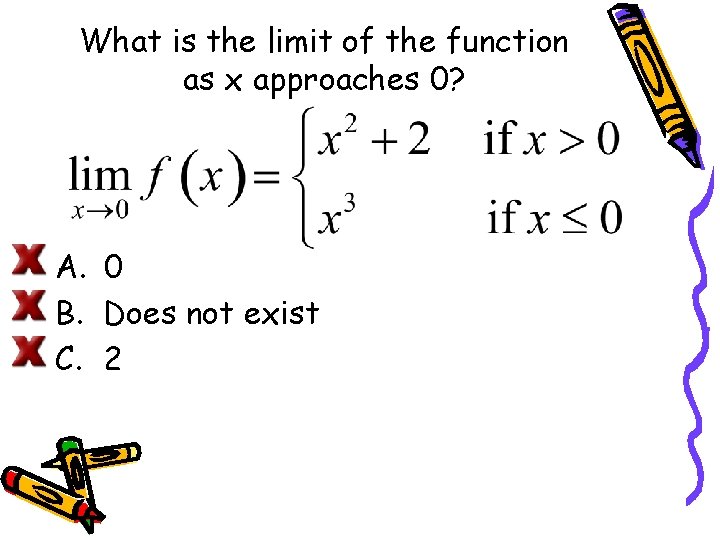
What is the limit of the function as x approaches 0? A. 0 B. Does not exist C. 2

UNBOUNDED BEHAVIOR • Consider the function This is a hyperbola with a vertical asymptote at • Notice that approaching x from either the left or the right of 0, f increases without bound, that is, f is approaching infinity, which is not an actual number. • Therefore, we say the finite limit does not exist.

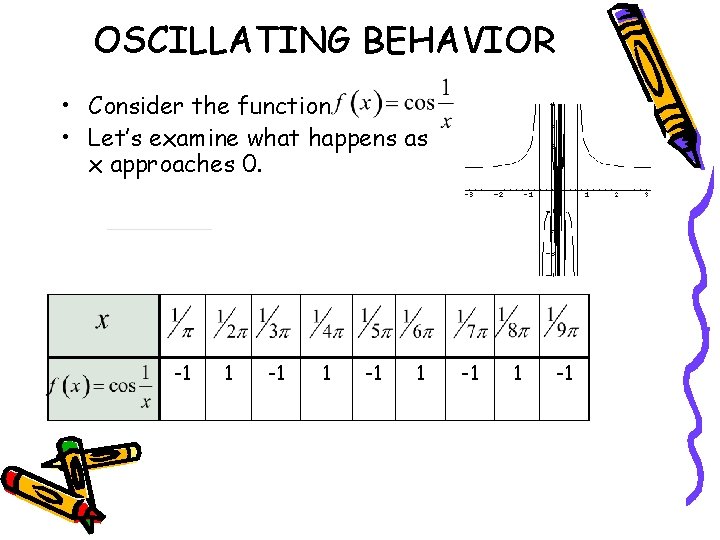
OSCILLATING BEHAVIOR • Consider the function • Let’s examine what happens as x approaches 0. -1 1 -1

Common Types of Behavior Associated with Nonexistence of a Limit • • • approaches a different number from the right side of c than it approaches from the left side. increases or decreases without bound as x approaches c. oscillates between two fixed values as x approaches c.

Formal Definition of Limit • Epsilon and delta Let f be a function defined on an open interval containing c (except possibly at c) and let L be a real number. The statement means that for each there exists a such that if then

Finding a for a given • Given the limit find delta given that epsilon is 0. 01. So where should you start? Hint: Math is all about definitions!