Finding Conjugate Orthogonal Diagonal Latin Squares Using Finite

Finding Conjugate Orthogonal Diagonal Latin Squares Using Finite Model Generators Hantao Zhang Jian Zhang 2012 -10 -26

Outline • Introduction (Latin squares, SAT, finite models) • Concepts and Definitions -- Conjugate Orthogonal Diagonal Latin Squares • Solution of an Open Case -- formalization in first-order logic • Conclusion

Introduction

Latin square problems • Latin squares (quasigroups) 123 312 231 012 201 120 • Challenging problems in mathematics – Counting problem – Existence of Latin squares with certain properties, e. g. , Mutually orthogonal Latin squares (MOLS)

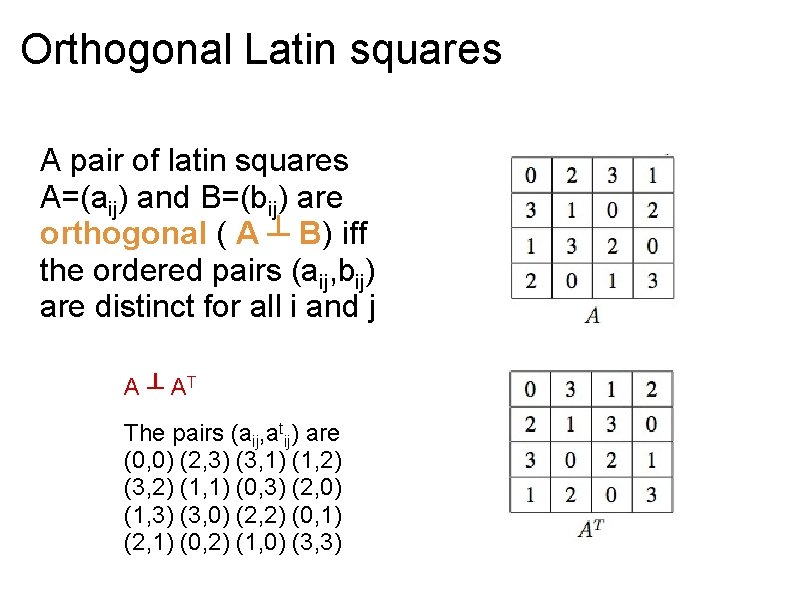
Orthogonal Latin squares A pair of latin squares A=(aij) and B=(bij) are orthogonal ( A ┴ B) iff the ordered pairs (aij, bij) are distinct for all i and j A ┴ AT The pairs (aij, atij) are (0, 0) (2, 3) (3, 1) (1, 2) (3, 2) (1, 1) (0, 3) (2, 0) (1, 3) (3, 0) (2, 2) (0, 1) (2, 1) (0, 2) (1, 0) (3, 3)

Solving Latin square problems with computers • Computer-aided research in combinatorics – existence of small Latin squares – crucial ! • Clement Lam and other mathematicians • AI researchers (using CSP / SAT / …) – Jian Zhang (1990/1991) – M. Fujita, J. Slaney, M. Stickel (IJCAI-1993, 1995) – Hantao Zhang, W. Mc. Cune, … – C. Gomes, O. Dubois and G. Dequen, …

SAT • Given a formula in the propositional logic, decide whether it is satisfiable or not. (p ∨ ┐q) ∧ (q ∨ ┐p) satisfiable: p = TRUE, q = TRUE. • • Many problems can be transformed into SAT. Tools (SAT solvers): SATO (1997), z. Chaff (2001), minisat (2005), …

Finite model generation/searching • Given a formula in the first-order logic, decide whether it is satisfiable or not in a fixed finite domain ([0, 1, …, n-1]). forall x, y, z: y≠z f(x, y) ≠f(x, z) forall x, y, z: x≠z f(x, y) ≠f(z, y) • Tools (finite model generators): Finder (~1994), SEM (1995), Mace 4 (~2003), …

• SEM input: 3. y = z | f(x, y) != f(x, z). x = z | f(x, y) != f(z, y). • SEM output: f|012 | 0|012 1|120 2|201

Mace 4 Input for qg 5. 8 assign(domain_size, 8). % clear(negprop). set(verbose). clauses(theory). x * z != y * z | x = y. x * y != x * z | y = z. x * x = x. (((y * x) * y) = x. end_of_list.

Mace 4 Output for qg 5. 8 interpretation( 8, [number=1, seconds=0], [ function(*(_, _), [ 0, 2, 6, 5, 1, 4, 7, 3, 7, 1, 5, 6, 2, 3, 0, 4, 3, 6, 2, 1, 5, 7, 4, 0, 1, 7, 4, 3, 0, 6, 2, 5, 6, 3, 0, 7, 4, 1, 5, 2, 2, 0, 3, 4, 7, 5, 1, 6, 5, 4, 7, 0, 3, 2, 6, 1, 4, 5, 1, 2, 6, 0, 3, 7 ]) ]).

Concepts and Definitions

• transversal in a Latin square: a set of positions, one per row and one per column, among which the elements {0, 1, …, n-1} occur exactly once each. • diagonal Latin square -- main diagonal is a transversal; back diagonal is also a transversal. • The following is a DLS: 0 2 3 1 0 2 1 3 2 0 1 3

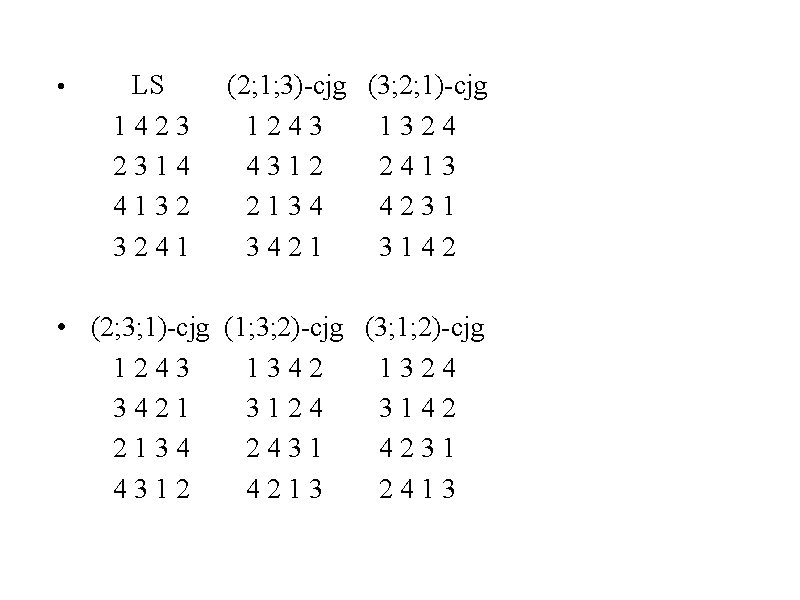
Conjugates • Given a Latin square defined by f(x, y), we may obtain its conjugates in the following way: • • • f 123(x, y) = z; f 132(x, z) = y; f 213(y, x) = z; f 231(y, z) = x; f 312(z, x) = y; f 321(z, y) = x.

• LS 1423 2314 4132 3241 (2; 1; 3)-cjg (3; 2; 1)-cjg 1243 1324 4312 2413 2134 4231 3421 3142 • (2; 3; 1)-cjg (1; 3; 2)-cjg (3; 1; 2)-cjg 1243 1342 1324 3421 3124 3142 2134 2431 4231 4312 4213 2413

Latin square with a hole Given a symbol set S and a subset H of S. If a Latin square L satisfies the following equations forall x, y, z: y≠z f(x, y) ≠f(x, z) forall x, y, z: y≠z f(y, x) ≠f(z, x) other than (x, y), (x, z), (y, x), (z, x) in H 2 we say L is a Latin square with the hole H. Example: S = { 0, 1, …, 7 } H = { 3, 4} 0 7 5 2 1 4 3 6 7 1 6 0 2 3 5 4 5 6 2 1 0 7 4 3 6 2 3 4 5 0 4 2 7 1 0 3 6 7 7 5 0 6 5 1 2 7 1 6 1 5 2 0 1 3 4 5 6 2 0 7

An Open Problem Given integers v and n, let ICODLS(v, n) denote a pair of orthogonal Latin squares (A, B) of order v with a hole of size n, where B is the (3, 2, 1)-conjugate of A; both A and B are diagonal. We knew the existence of ICODLS(v, n) for all possible feasible values, except possibly (n, v) = (11, 3). Example: ICODLS(8, 2) 0 7 5 2 1 4 3 6 7 1 6 0 2 3 5 4 5 6 2 1 0 7 4 3 6 2 3 4 5 0 4 2 7 1 0 3 6 7 A 7 5 0 6 5 1 2 7 1 6 1 5 2 0 1 3 4 5 6 2 0 7 0 4 3 6 5 2 7 1 3 1 4 5 7 6 2 0 4 3 2 7 6 0 1 5 5 1 2 7 7 2 6 5 6 0 7 1 0 2 B 1 0 1 7 5 4 0 5 3 6 2 6 4 3 6 0 5 1 2 3 4 7

Solution of an Open Case

First Order Logic Formulas Latin Square Constraints: A(x, y) = A(x, z) → y = z A(x, y) = A(z, y) → x = z A┴B: A(x 1, y 1)=A(x 2, y 2) ∧ B(x 1, y 1)=B(x 2, y 2) → x 1=x 2 ∧ y 1=y 2 Latin Square Constraints with a hole: (A(x, y) = A(x, z) → y = z) / h(x, y) / h(x, z) (A(x, y) = A(z, y) → x = z) / h(x, y) / h(z, y) A┴B: (A(x 1, y 1)=A(x 2, y 2) ∧ B(x 1, y 1)=B(x 2, y 2) → x 1=x 2 ∧ y 1=y 2) / h(x 1, y 1) / h(x 2, y 2)

Finding the ICODLS with SAT solvers • Generating propositional formulas: Introduce boolean variables Vijk (i, j, k ∈ [0, n-1]) Vijk = 1 iff A(i, j) = k Vijk = 0 iff A(i, j) ≠ k • Using SAT solvers (minisat, Glucose) not completed (> two weeks)

set(arithmetic). assign(domain_size, 11). assign(selection_order, 2). op(400, infix, [@, g, f]). formulas(theory). % define hole h(4, 4). h(4, 5). h(4, 6). h(5, 5). h(5, 6). h(6, 6). -h(y, x) | h(x, y). -h(x, y) | x = 4 | x = 5 | x = 6. -h(y, x) | x = 4 | x = 5 | x = 6. x @ y != z | -h(x, z). x @ y != z | -h(y, z). Mace 4 input

% define main and back diagonals x = y | (x @ x) != (y @ y) | h(x, x) | h(y, y). x = y | (x @ SUB(10, x)) != (y @ SUB(10, y)) | h(x, SUB(10, x)) | h(y, SUB(10, y)). x = y | z @ x != x | z @ y != y | h(z, x) | h(z, y). x = y | z @ SUB(10, x) != x | z @ SUB(10, y) != y | h(x, SUB(10, x)) | h(y, SUB(10, y)). Mace 4 input (cont. ) % quasigroup axioms (equational) x @ (x g y) = y | h(x, y). x g (x @ y) = y | h(x, y). (x f y) @ y = x | h(x, y). (x @ y) f y = x | h(x, y). % Orthogonal to its (3, 2, 1)-conjugate (u @ y) @ y != (u @ w) @ w | y = w | h(u, y) | h(u, w) | h(w, y). end_of_list.

==== DOMAIN SIZE 11====== MODEL ========== interpretation( 11, [number=1, seconds=1154566], [ function(@(_, _), [ 3, 9, 2, 5, 7, 8, 0, 10, 6, 4, 1, 0, 2, 9, 6, 8, 7, 1, 3, 4, 10, 5, 8, 4, 7, 3, 10, 1, 2, 5, 9, 6, 0, 4, 6, 5, 10, 9, 0, 3, 2, 8, 1, 7, 9, 0, 10, 8, 0, 0, 0, 1, 7, 3, 2, 1, 10, 0, 2, 0, 0, 0, 9, 3, 7, 8, 2, 7, 1, 9, 0, 0, 10, 8, 3, 5, 3, 4, 0, 1, 10, 7, 8, 2, 9, 6, 6, 5, 3, 7, 0, 9, 8, 4, 1, 2, 10, 8, 6, 1, 2, 3, 9, 7, 5, 0, 4, 7, 1, 8, 4, 3, 2, 10, 6, 0, 5, 9 ]), …… Mace 4 Output

Conclusion ØWe solved an open case: existence of (3, 2, 1)-ICODLS(11, 3). ØWe presented the formalization of the problem in FOL. ØOther cases remain open: e. g. , the existence of (3, 2, 1)-CODLS(10), … Challenging benchmarks for constraint solving, SAT solving and finite model generation.

Thank you!