Finding areas of Regular Polygons Special Right Triangles

Finding areas of Regular Polygons: Special Right Triangles

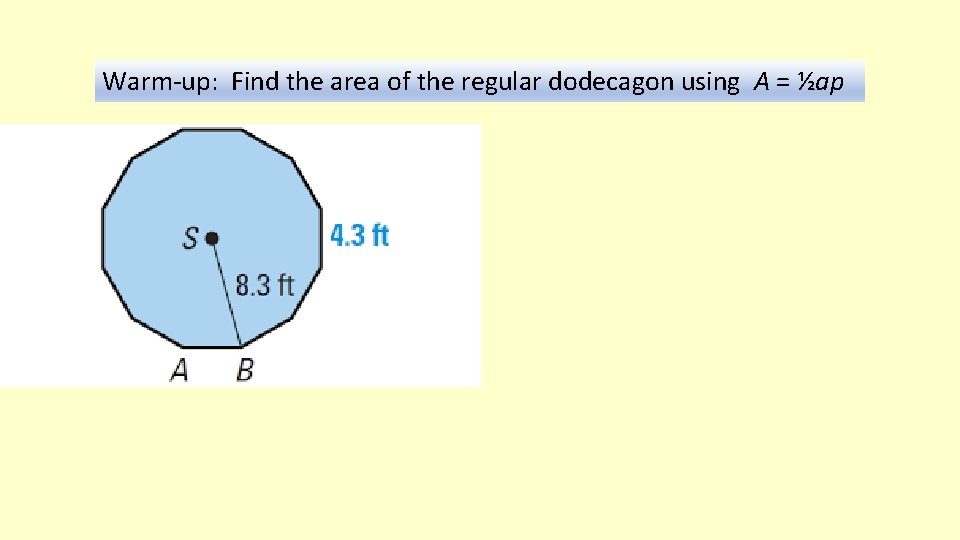
Warm-up: Find the area of the regular dodecagon using A = ½ap

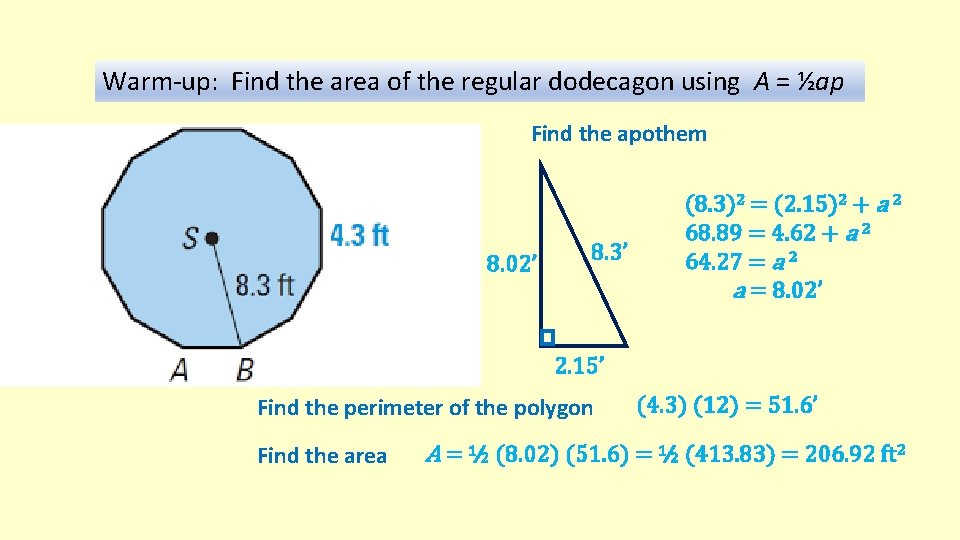
Warm-up: Find the area of the regular dodecagon using A = ½ap Find the apothem 8. 02’ 8. 3’ (8. 3)2 = (2. 15)2 + a 2 68. 89 = 4. 62 + a 2 64. 27 = a 2 a = 8. 02’ 2. 15’ Find the perimeter of the polygon Find the area (4. 3) (12) = 51. 6’ A = ½ (8. 02) (51. 6) = ½ (413. 83) = 206. 92 ft 2

Finding the area of a square using A = ½ap We know what the answer is, so this is a good way to test our regular polygon formula. 8” Step 1: Draw a right triangle containing a radius and apothem. Step 2: Find the central angle measure of the polygon. 90 o Then, find half its measure and put it in your triangle. 45 o 4” 4” Step 3: Find the measures of the sides of the triangle in simplest radical form using special right triangle rules. Step 4: Use the regular polygon formula to find the area of the square. A = ½ap A = ½ (4)(32) = ½ (128) = 64 in 2

Finding the area of an equilateral triangle using A = ½ap The perimeter of the triangle is 36”. Step 1: Draw a right triangle containing a radius and apothem. 12” 5 o 60 o 6” Step 2: Find the central angle measure of the polygon. 120 o Then, find half its measure and put it in your triangle. Step 3: Find the measures of the sides of the triangle in simplest radical form using special right triangle rules. Step 4: Use the regular polygon formula to find the area of the triangle. A = ½ap

Finding the area of a regular hexagon using A = ½ap The radius of the hexagon is 10”. Step 1: Draw a right triangle containing a radius and apothem. 30 o Step 2: Find the central angle measure of the polygon. 60 o Then, find half its measure and put it in your triangle. 10” Step 3: Find the measures of the sides of the triangle in simplest radical form using special right triangle rules. 5” Step 4: Use the regular polygon formula to find the area of the hexagon. A = ½ap

Areas of Composite Figures A composite figure is one that can be divided into familiar nonoverlapping shapes. For example, this figure can be divided into an isosceles triangle and a semicircle. Find the area of the isosceles triangle. A(triangle) = ½ bh = ½(22)(16) = 176 cm 2 Find the area of the semicircle. A(semicircle) = ½ (380. 13) = 190. 07 cm 2 Use the area addition postulate.

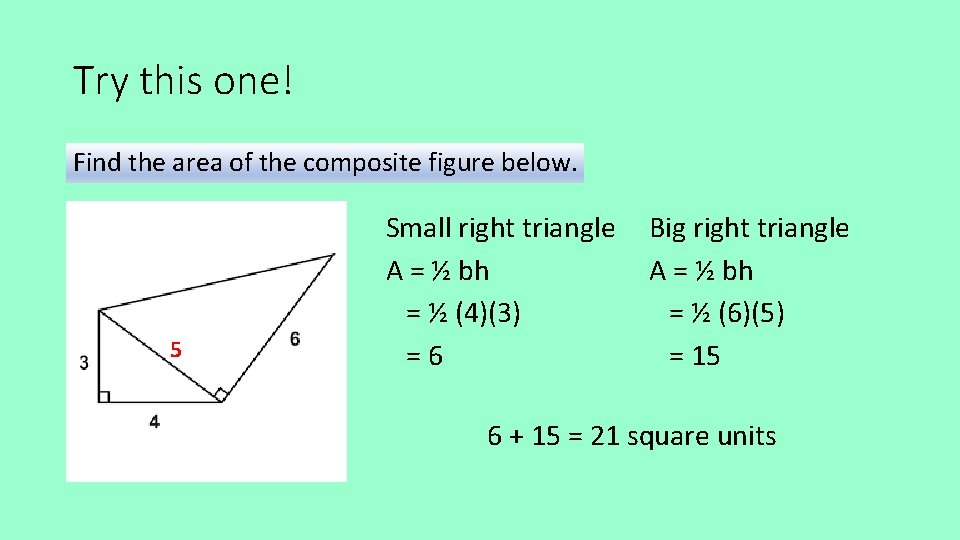
Try this one! Find the area of the composite figure below. 5 Small right triangle A = ½ bh = ½ (4)(3) =6 Big right triangle A = ½ bh = ½ (6)(5) = 15 6 + 15 = 21 square units

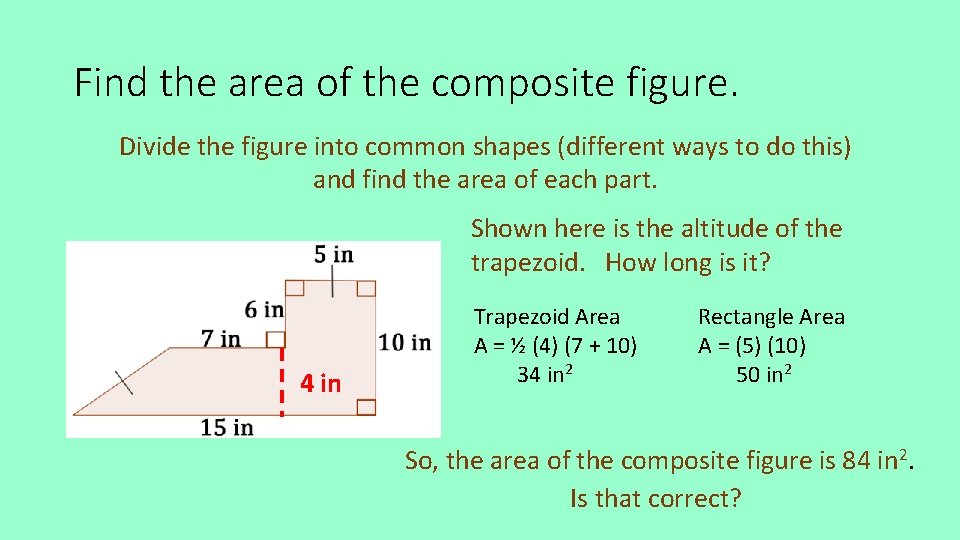
Find the area of the composite figure. Divide the figure into common shapes (different ways to do this) and find the area of each part. Shown here is the altitude of the trapezoid. How long is it? 4 in Trapezoid Area A = ½ (4) (7 + 10) 34 in 2 Rectangle Area A = (5) (10) 50 in 2 So, the area of the composite figure is 84 in 2. Is that correct?

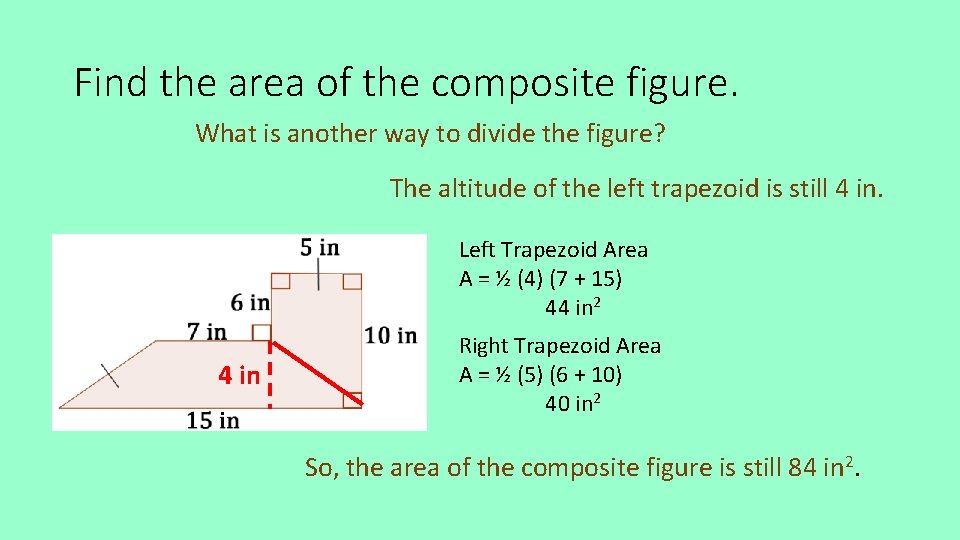
Find the area of the composite figure. What is another way to divide the figure? The altitude of the left trapezoid is still 4 in. Left Trapezoid Area A = ½ (4) (7 + 15) 44 in 2 4 in Right Trapezoid Area A = ½ (5) (6 + 10) 40 in 2 So, the area of the composite figure is still 84 in 2.

Homework: Due Thursday, 5/28 @ 3 pm • Finish Regular Polygon Areas Worksheet • Pages 614 -615 (21, 22, 25, 26, 28, 33 -35, 38, 44) • Areas Composite Shapes (1 -8)