Finding an Exponential Regression Use the data in

Finding an Exponential Regression Use the data in the program file COOL to find an exponential model.

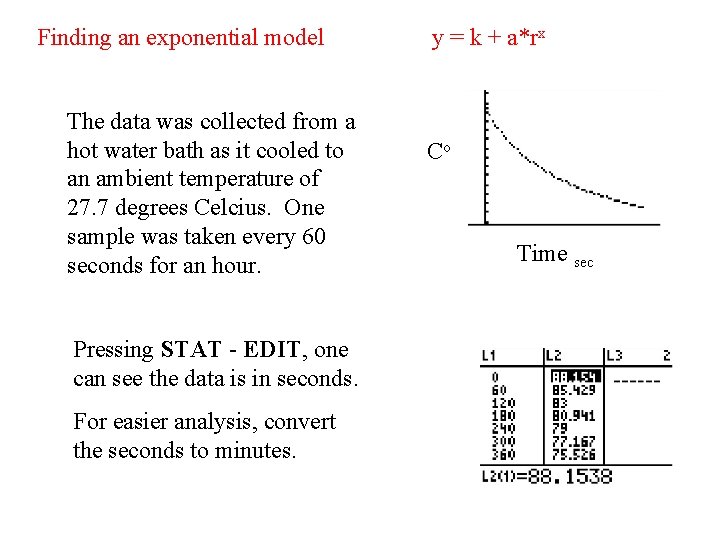
Finding an exponential model The data was collected from a hot water bath as it cooled to an ambient temperature of 27. 7 degrees Celcius. One sample was taken every 60 seconds for an hour. Pressing STAT - EDIT, one can see the data is in seconds. For easier analysis, convert the seconds to minutes. y = k + a*rx Co Time sec

Finding an exponential model To convert time from seconds to minutes, divide by 60. Place the cursor on L 1. Enter the formula L 1/60 and press ENTER. The data will reflect the conversion and appear similar to the table at the right. To redraw the graph with the new coordinates, press ZOOMSTAT (Zoom - 9) y = k + a*rx

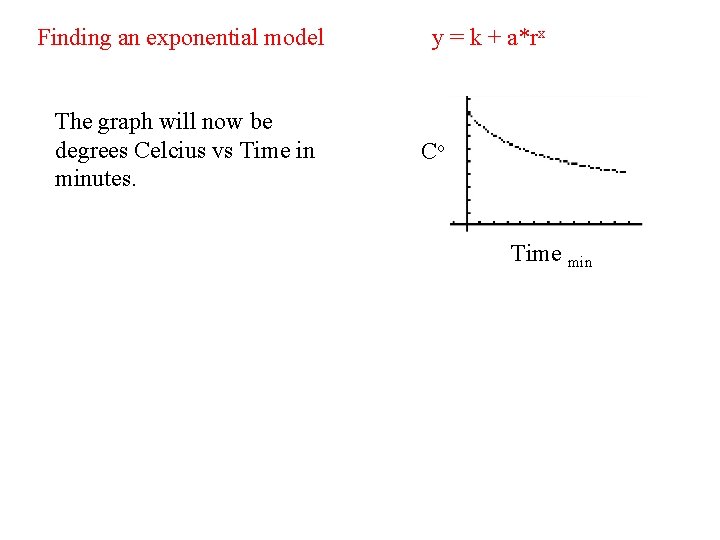
Finding an exponential model The graph will now be degrees Celcius vs Time in minutes. y = k + a*rx Co Time min

Finding an exponential model y = k + a*rx Solving Algebraically: Step 1 - Find k The exponential model y = k + a*rx will approach y = k as x approaches infinity if 0 < r < 1. Since the ambient room temperature was reported to be 27. 7 o C, the water will approach room temperature and k = 27. 7 o C

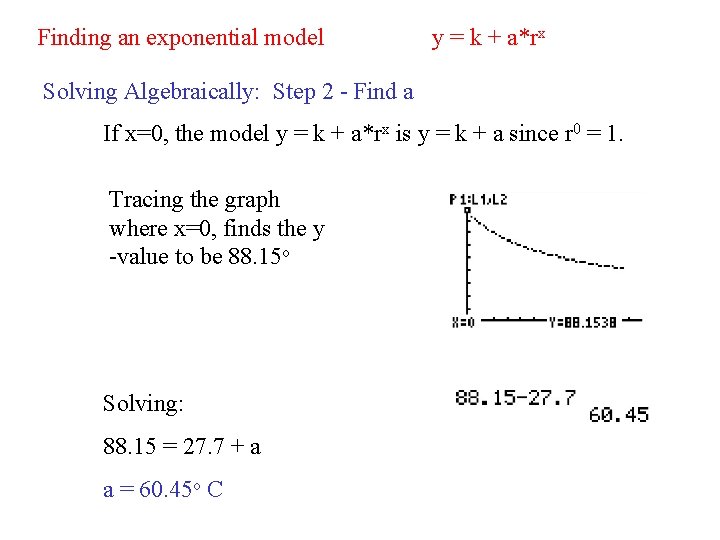
Finding an exponential model y = k + a*rx Solving Algebraically: Step 2 - Find a If x=0, the model y = k + a*rx is y = k + a since r 0 = 1. Tracing the graph where x=0, finds the y -value to be 88. 15 o Solving: 88. 15 = 27. 7 + a a = 60. 45 o C

Finding an exponential model y = k + a*rx Solving Algebraically: Step 3 - Find r Choose another ordered pair (x, y) and solve for ‘r’. Trace to find another point on the graph to substitute.

Finding an exponential model y = k + a*rx Solving Algebraically: Step 3 - Find ‘r’ (con’t) Substituting (50, 43. 92) and solving for ‘r’: 43. 92 o =27. 7 o + 60. 45 o * r 50 43. 92 o - 27. 7 o 60. 45 o ( = r 50 ) (43. 92 o - 27. 7 o) 60. 45 o 1 50 =r r = 0. 9740

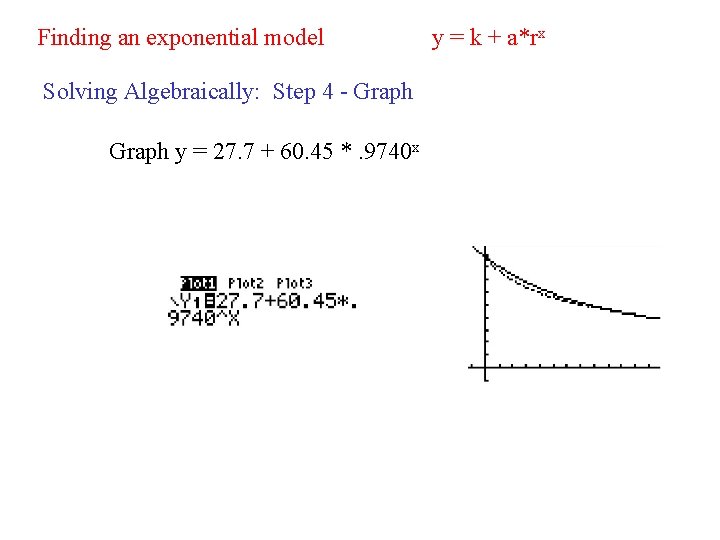
Finding an exponential model Solving Algebraically: Step 4 - Graph y = 27. 7 + 60. 45 *. 9740 x y = k + a*rx

Finding an exponential model y = k + a*rx Using a regression: Step 1 - Shift the data to approach zero The TI-83 exponential regression is in the form of y = a*bx which assumes the model will approach 0 as x approaches infinity. Since our data approaches 27. 7, we must shift the data down so that it will approach 0. After the regression is complete, the model will be shifted back up the 27. 7 degrees. Press STAT - EDIT and place the cursor on L 3. Enter the formula L 2 - 27. 7 and press ENTER. L 3 will be the temperature reduced to approach 0.

Finding an exponential model y = k + a*rx Using a regression: Step 1 - Shift the data to approach zero The data in L 3 will appear as: Using a regression: Step 2 - Fit the regression. Press STAT - CALC and choose Exp. Reg.

Finding an exponential model y = k + a*rx Using a regression: Step 2 - Fit the regression. The y-values are in L 3. Set the regression for the x-values in L 1 and the yvalues in L 3. The resulting equation was stored in Y 2 The resulting regression must be shifted up by 27. 7 degrees to fit the original data. (con’t)

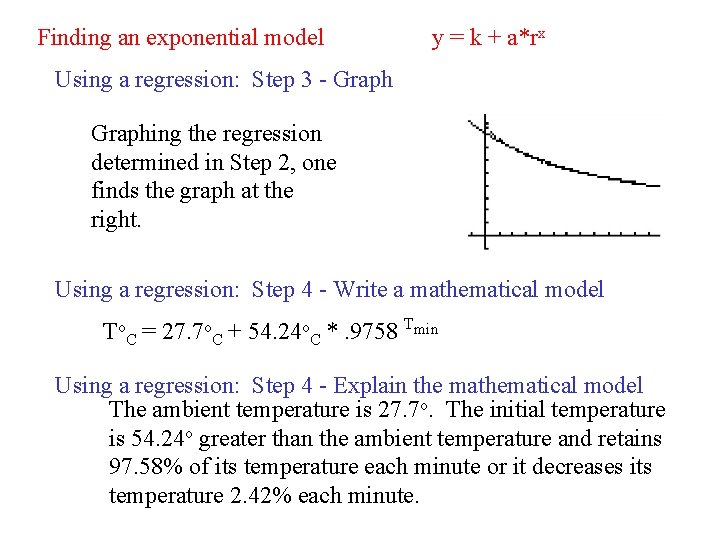
Finding an exponential model y = k + a*rx Using a regression: Step 3 - Graphing the regression determined in Step 2, one finds the graph at the right. Using a regression: Step 4 - Write a mathematical model To. C = 27. 7 o. C + 54. 24 o. C *. 9758 Tmin Using a regression: Step 4 - Explain the mathematical model The ambient temperature is 27. 7 o. The initial temperature is 54. 24 o greater than the ambient temperature and retains 97. 58% of its temperature each minute or it decreases its temperature 2. 42% each minute.