Finding a Hamiltonian path on a folded DNA

Finding a Hamiltonian path on a folded DNA shape Hanny Seaman Advisors: Dr. Ido Bachelet Prof. Ron Unger 2013 The Mina and Everard Goodman Faculty of Life Sciences , Bar-Ilan University Ramat-Gan

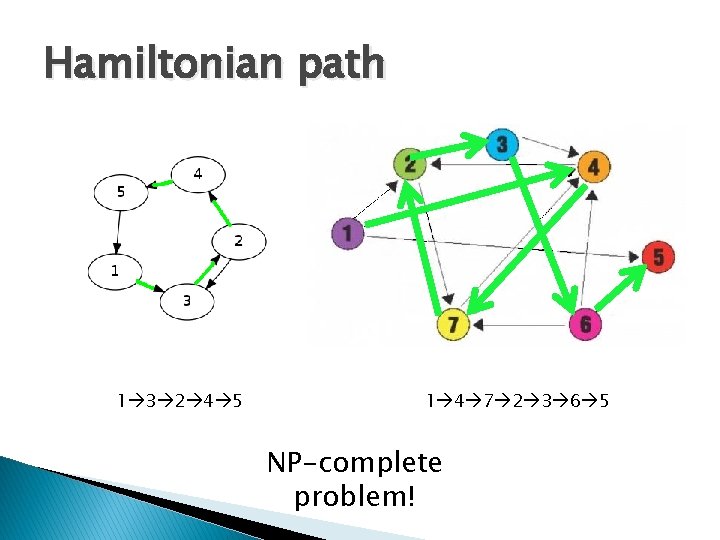
Hamiltonian path 1 3 2 4 5 1 4 7 2 3 6 5 NP-complete problem!

Adleman’s solution � DNA strands represent vertices and paths of a 7 -node graph � Mix in tube – self complementarity � Filtration

Origami DNA � Folding of DNA to create nanoscale shapes � Terminology: ◦ Scaffold ◦ Staples � ca. DNAno

Representing the graph � Example: 0 4 vertices

Representing the graph � Example: 0 1 4 vertices

Representing the graph � Example: 0 1 2 4 vertices

Representing the graph � Example: 0 1 3 2 4 vertices

Representing the graph � Example: 0 1 3 2 4 vertices

Representing the graph � Example: 0 1 3 2 4 vertices

Representing the graph � Example: 0 1 3 2 4 vertices

Representing the graph � Example: 0 1 3 2 4 vertices

Representing the graph � Example: 0 1 3 2 4 vertices

Representing the graph � Example: 0 1 3 2 4 vertices

Representing the graph � Example: 0 1 3 2 4 vertices

Example: 4 vertices Start End Sequence Length Color 0[45] 0[26] GGGCGAAAAACCGTCTATCA 20 #aaaa 00 0[64] 0[46] CGTGGACTCCAACGTCAAA 19 #cc 0000 1[26] 1[45] TGTTGTTCCAGTTTGGAACA 20 #f 74308 1[46] 1[64] AGAGTCCACTATTAAAGAA 19 #03 b 6 a 2 2[45] 2[26] TAGCCCGAGATAGGGTTGAG 20 #03 b 6 a 2 2[64] 2[46] CCCTTATAAATCAAAAGAA 19 #aaaa 00 3[26] 3[45] GAAAATCCTGTTTGATGGTG 20 #f 7931 e 3[46] 3[64] GTTCCGAAATCGGCAAAAT 19 #007200

Example: 4 vertices Edges details

Example: 4 vertices Scaffold details

7 vertices – planning the graph Calculate the edges and vertices sequences

7 vertices – planning the graph 1 2 3 7 6 4 5

Experiments

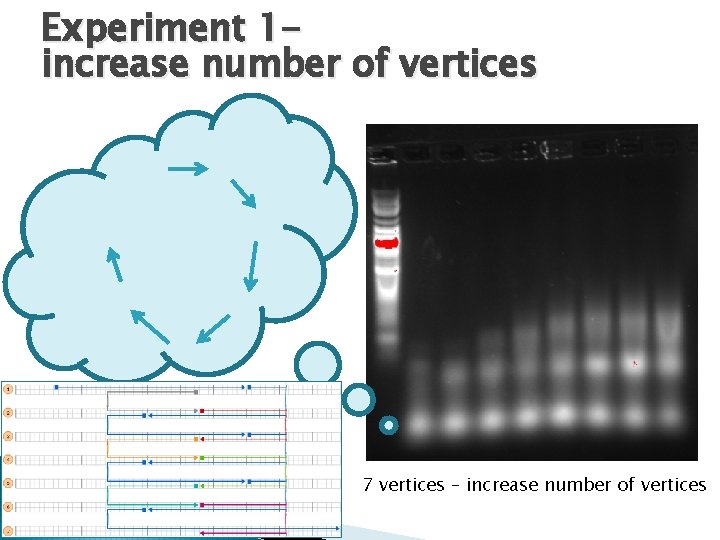
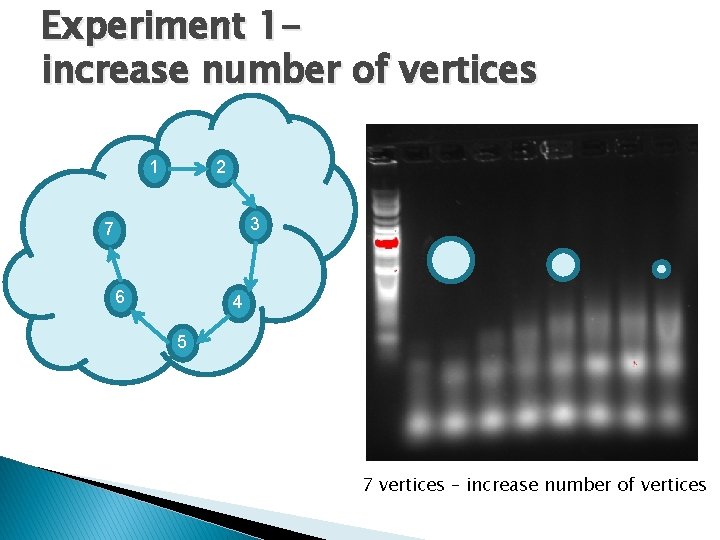
Experiment 1 increase number of vertices 7 vertices – increase number of vertices

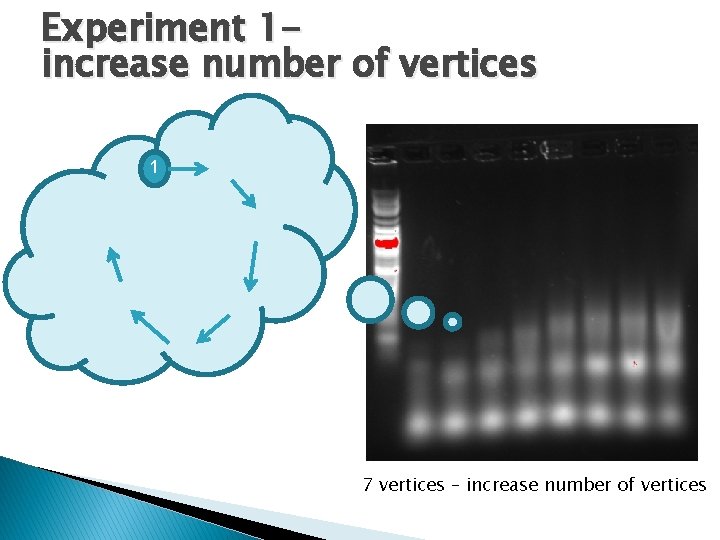
Experiment 1 increase number of vertices 1 7 vertices – increase number of vertices

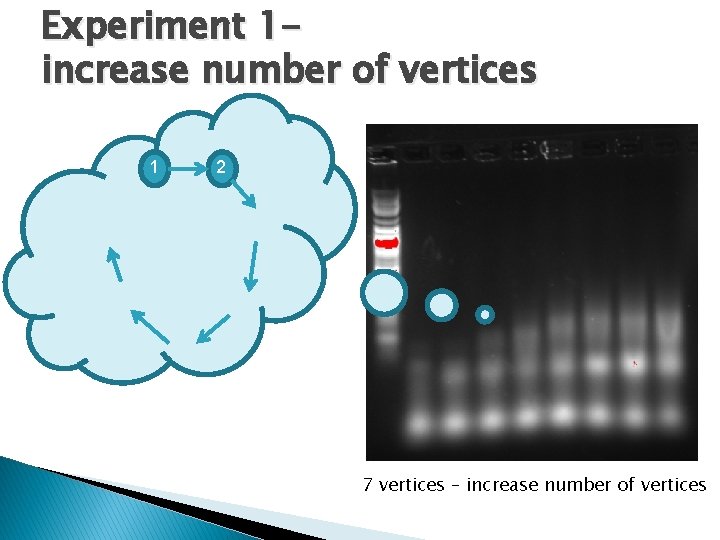
Experiment 1 increase number of vertices 1 2 7 vertices – increase number of vertices

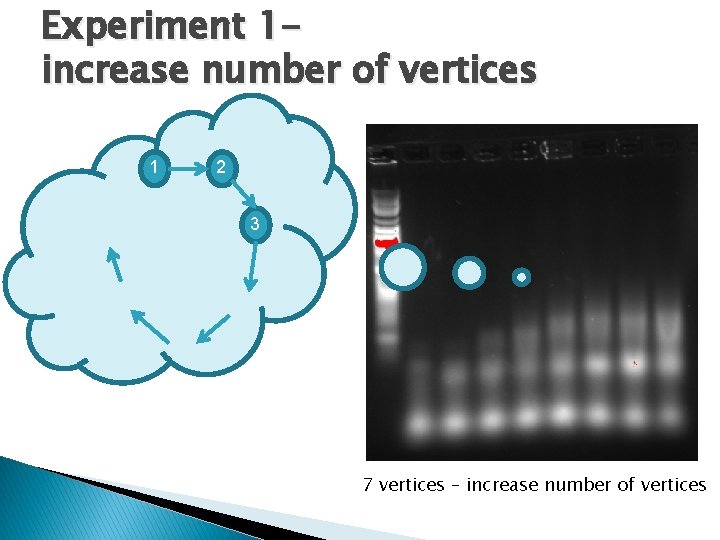
Experiment 1 increase number of vertices 1 2 3 7 vertices – increase number of vertices

Experiment 1 increase number of vertices 1 2 3 7 6 4 5 7 vertices – increase number of vertices

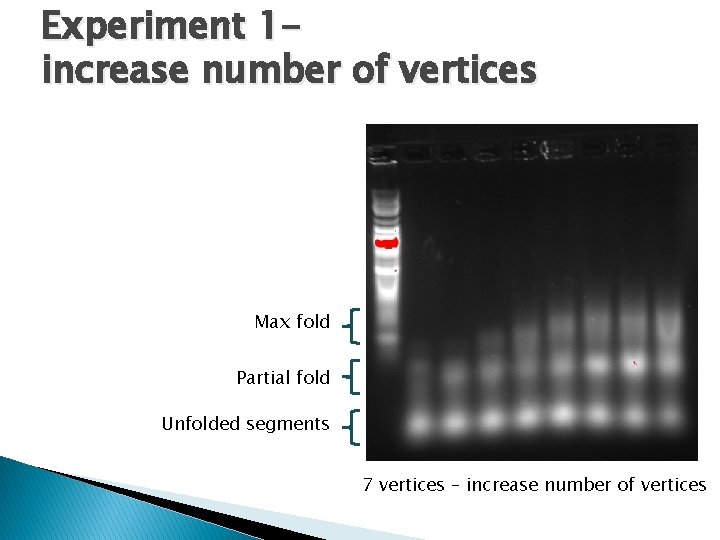
Experiment 1 increase number of vertices Max fold Partial fold Unfolded segments 7 vertices – increase number of vertices

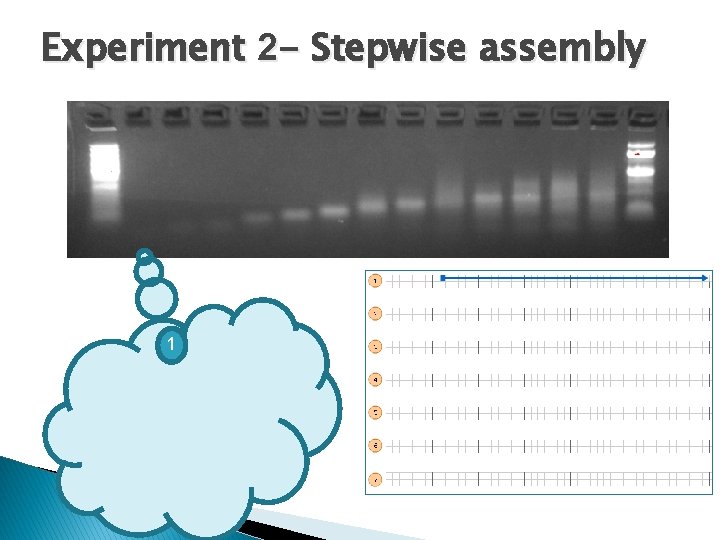
Experiment 2 - Stepwise assembly 1

Experiment 2 - Stepwise assembly 1

Experiment 2 - Stepwise assembly 1 2

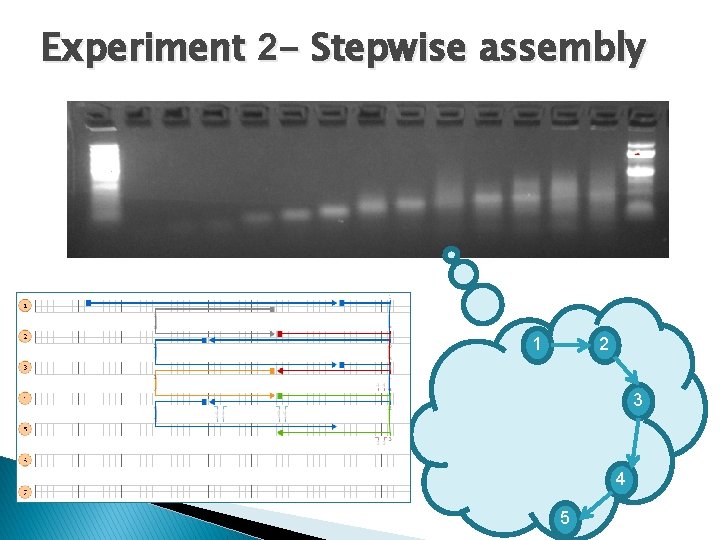
Experiment 2 - Stepwise assembly 1 2 3 4 5

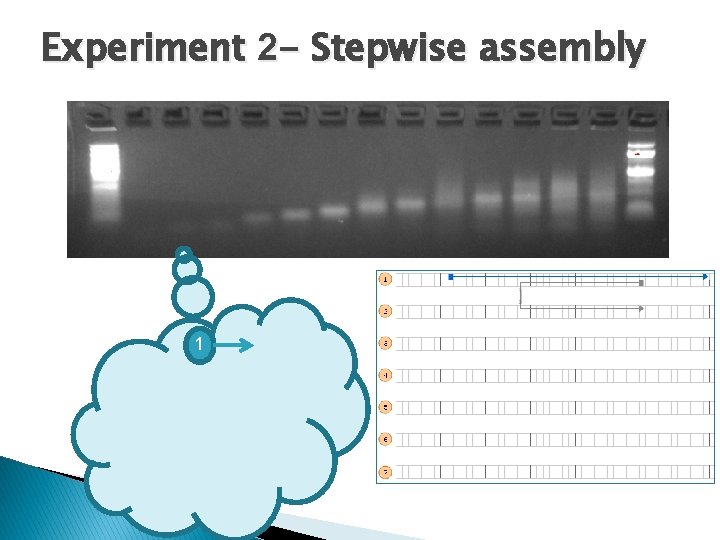
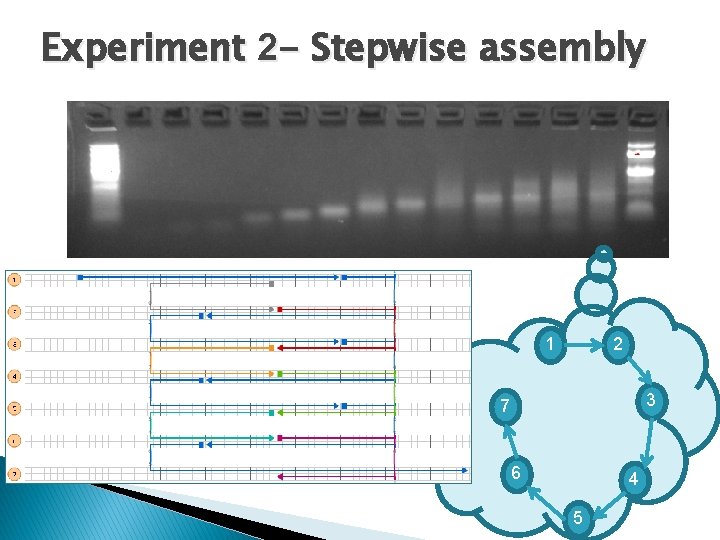
Experiment 2 - Stepwise assembly 1 2 3 7 6 4 5

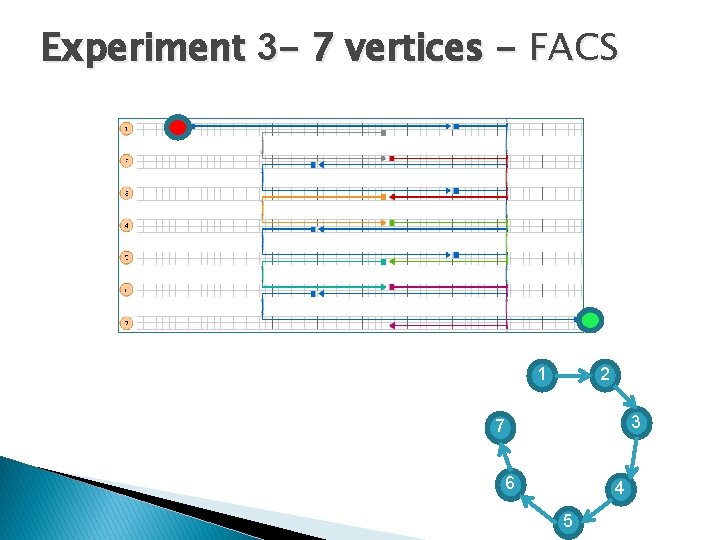
Experiment 3 - 7 vertices - FACS 1 2 3 7 6 4 5

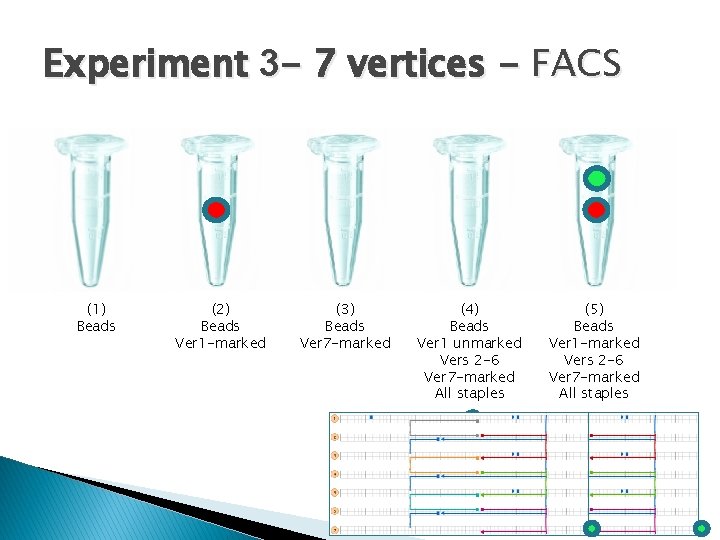
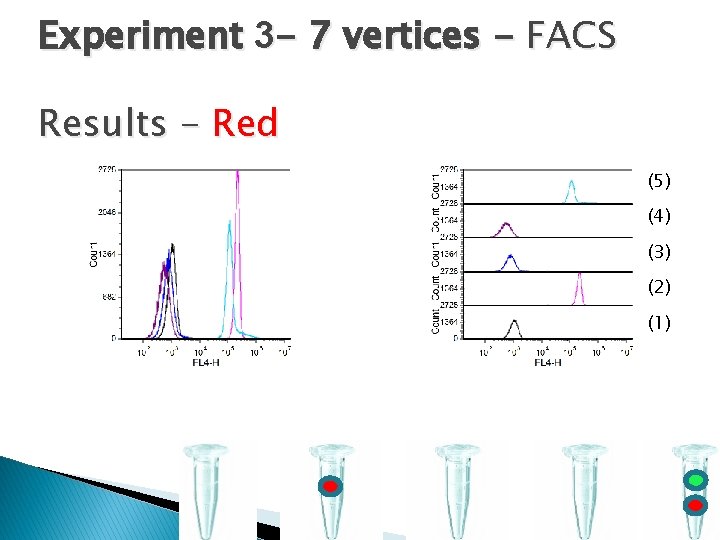
Experiment 3 - 7 vertices - FACS (1) Beads (2) Beads Ver 1 -marked (3) Beads Ver 7 -marked (4) Beads Ver 1 unmarked Vers 2 -6 Ver 7 -marked All staples (5) Beads Ver 1 -marked Vers 2 -6 Ver 7 -marked All staples

Experiment 3 - 7 vertices - FACS Results - Red (5) (4) (3) (2) (1)

Experiment 3 - 7 vertices - FACS Results - Green (5) (4) (3) (2) (1)

Summary � Representing � Find graph using origami DNA if exists a Hamiltonian Path

What’s next? � Watching folded DNA using AFM � Experiments with: ◦ edges including poly. T ◦ Large number of vertices ◦ Graph with several paths – not only Hamiltonian