Find the mean median mode and range of

• Find the mean, median, mode, and range of the following set of data. • 3, 4, 5, 5, 8, 9, 12, 14 • Mean = • Median = • Mode = • Range =

Math II B Day 2 (1 -5 -11) Standard MM 2 D 1 B • Understand calculate the means and standard deviations of sets of data Today’s Question: What are measures of spread? How do we calculate standard deviation and what does it mean?

Welcome to the wonderful world of Statistics

Some quotes on Statistics "There are three kinds of lies: lies, damned lies and statistics. " - Mark Twain “ 65% of all statistics are made up. Including this one" - Dilbert There are two kinds of statistics, the kind you look up and the kind you make up. - Rex Stout

Describing Data

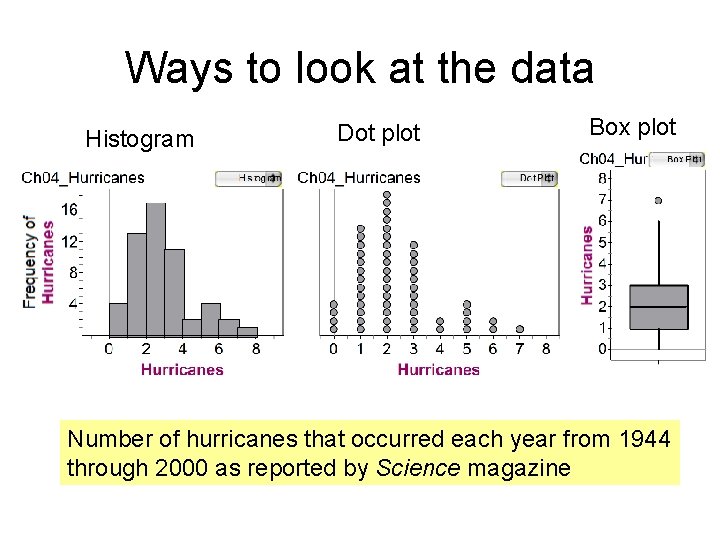
Ways to look at the data Histogram Dot plot Box plot Number of hurricanes that occurred each year from 1944 through 2000 as reported by Science magazine

3 Characteristics of data Shape Center Spread

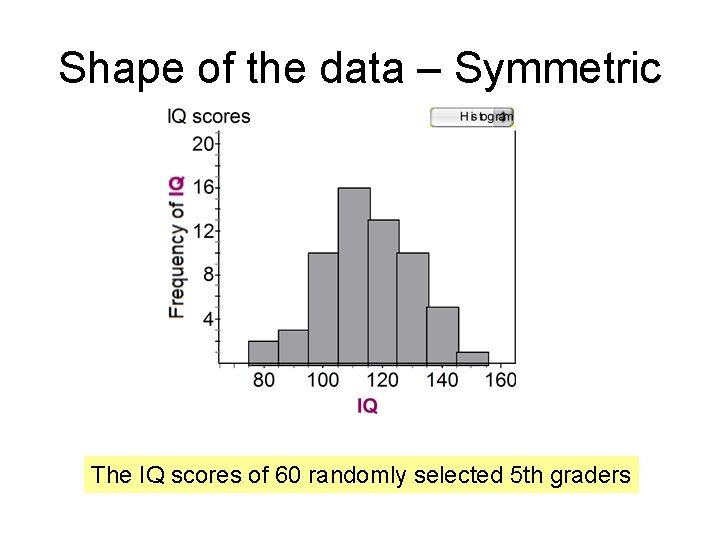
Shape of the data – Symmetric The IQ scores of 60 randomly selected 5 th graders

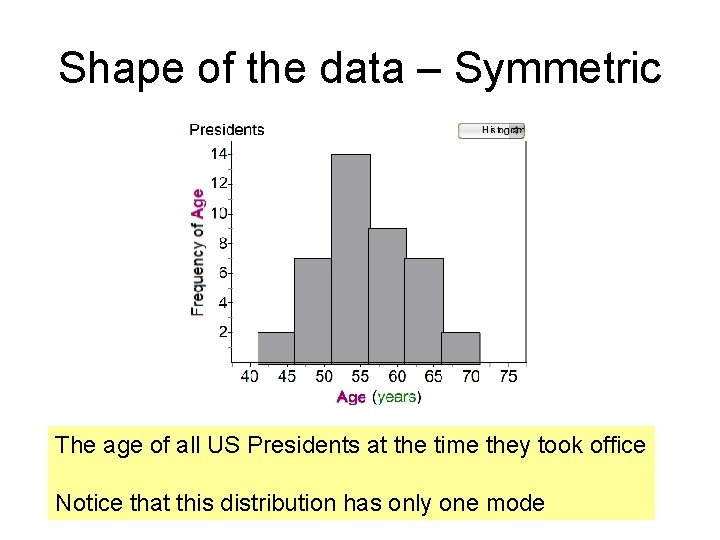
Shape of the data – Symmetric The age of all US Presidents at the time they took office Notice that this distribution has only one mode

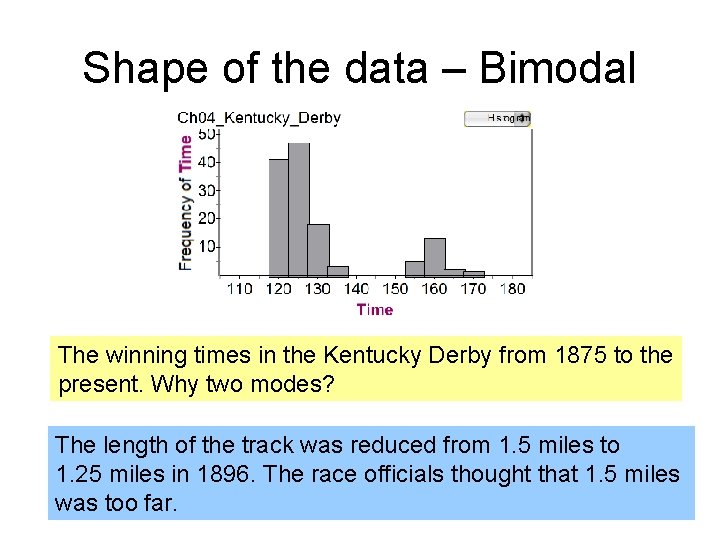
Shape of the data – Bimodal The winning times in the Kentucky Derby from 1875 to the present. Why two modes? The length of the track was reduced from 1. 5 miles to 1. 25 miles in 1896. The race officials thought that 1. 5 miles was too far.

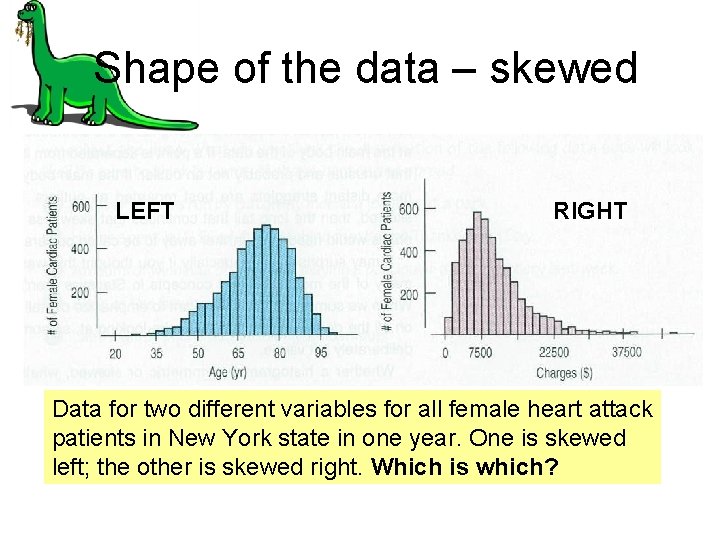
Shape of the data – skewed LEFT RIGHT Data for two different variables for all female heart attack patients in New York state in one year. One is skewed left; the other is skewed right. Which is which?

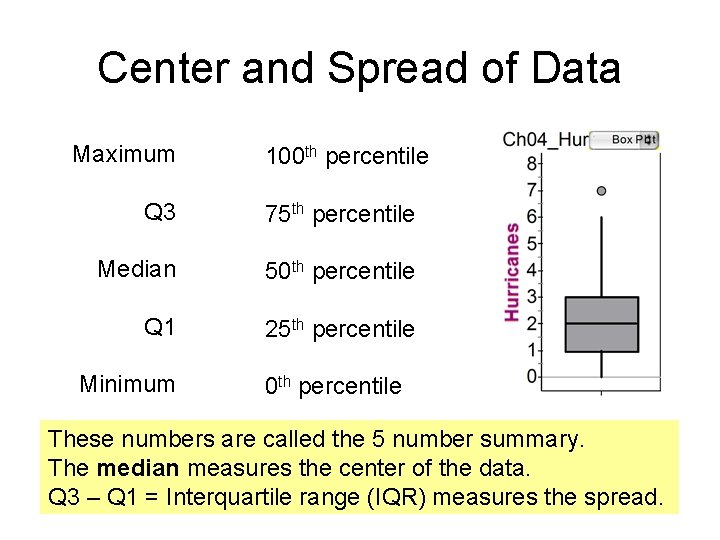
Center and Spread of Data Maximum 100 th percentile Q 3 75 th percentile Median 50 th percentile Q 1 25 th percentile Minimum 0 th percentile These numbers are called the 5 number summary. The median measures the center of the data. Q 3 – Q 1 = Interquartile range (IQR) measures the spread.

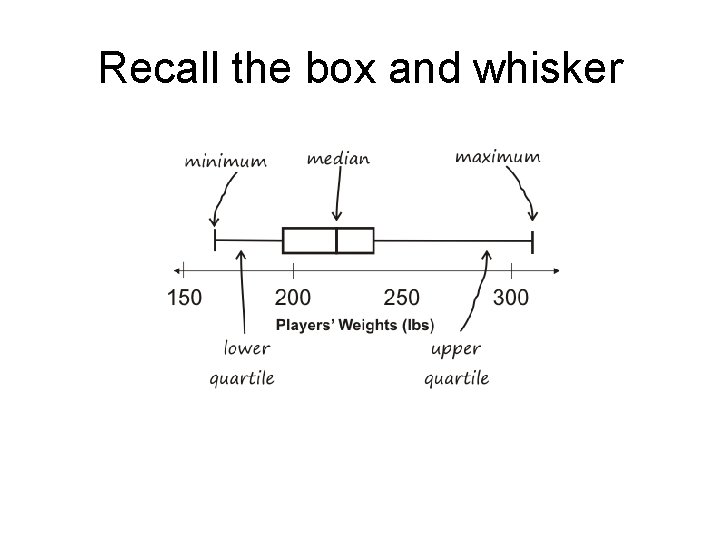
Recall the box and whisker

Create a Box and Whisker for both cities • Miami weather • 76, 78, 81, 84, 87, 90, 91, 89, 85, 81, 78 • Atlanta weather • 50, 55, 63, 71, 78, 84, 88, 86, 81, 72, 62, 53

Temperatures in 3 cities Which city’s temperatures are the 1. most spread out ? 2. most consistent ?

You try…. . Which salesperson is more consistent and why?

Measures of Central Tendency and Dispersion Central Tendency: Mean, Median, and Mode Dispersion or Spread: Range, IQR, Standard Deviation, and Variance Examples of Uses for Standard Deviation and Variance: • • Factory Processes Stocks Weather Sports Teams Grades Attendance to events ? ? ?

What are Variance and Standard Deviation

Symbols: • s 2 = Sample Variance • s = Sample Standard Deviation • 2 = Population Variance • = Population Standard Deviation • -- x = Mean

Center and spread of data The square root of the variance. This quantity has the same units as the data. This is one of the most common measures of the spread of a distribution. The formula given above is for the population standard deviation.

Center and spread of data Mean Absolute Deviation Variance Standard Deviation

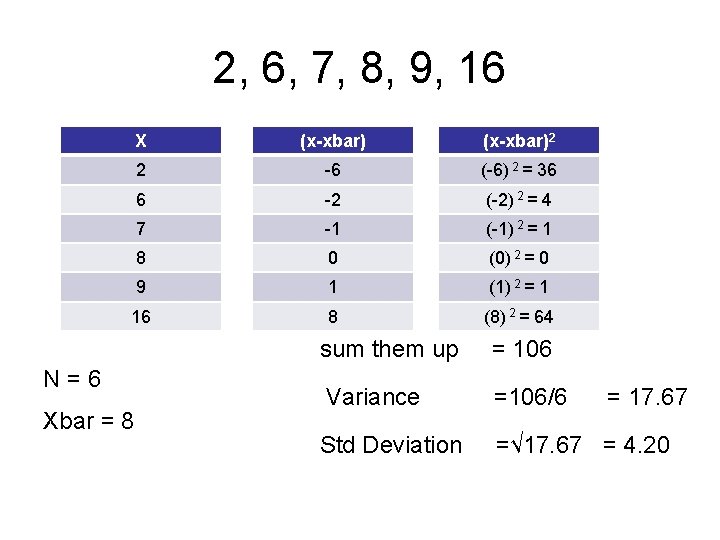
2, 6, 7, 8, 9, 16 X (x-xbar)2 2 -6 (-6) 2 = 36 6 -2 (-2) 2 = 4 7 -1 (-1) 2 = 1 8 0 (0) 2 = 0 9 1 (1) 2 = 1 16 8 (8) 2 = 64 N=6 Xbar = 8 sum them up = 106 Variance =106/6 Std Deviation =√ 17. 67 = 4. 20 = 17. 67

Now let’s try another on the promethean board 3, 4, 4, 8, 11

You try…. . 2, 4, 5, 6, 8

Find the mean, range, variance and std. deviation of the following 1) 2) 3) 4) 5) 2, 5, 6, 6, 7 9, 7, 6, 2, 3 1, 1, 5, 6, 7 8, 5, 6, 7, 3 4, 8, 1, 0, 3 Identify the following: Which data group has the largest mean, std. deviation, and range.

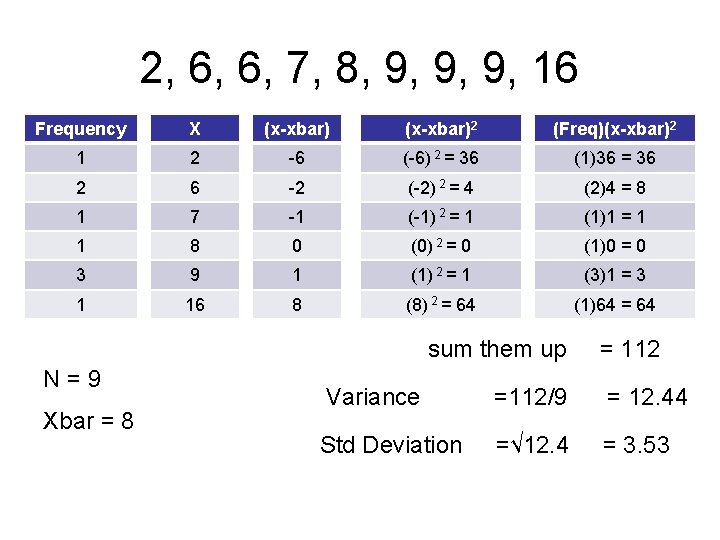
2, 6, 6, 7, 8, 9, 9, 9, 16 Frequency X (x-xbar)2 (Freq)(x-xbar)2 1 2 -6 (-6) 2 = 36 (1)36 = 36 2 6 -2 (-2) 2 = 4 (2)4 = 8 1 7 -1 (-1) 2 = 1 (1)1 = 1 1 8 0 (0) 2 = 0 (1)0 = 0 3 9 1 (1) 2 = 1 (3)1 = 3 1 16 8 (8) 2 = 64 (1)64 = 64 sum them up N=9 Xbar = 8 = 112 Variance =112/9 = 12. 44 Std Deviation =√ 12. 4 = 3. 53

Homework Page 261 #13 -17 Show all of your work for standard deviation or no credit